Навигация
Методы оценивания коэффициентов отражения
1.4.3. Методы оценивания коэффициентов отражения.
Рекурсивное решение уравнений Юла-Уалкера методом Левинсона связывает АР-параметры порядка p c параметрами порядка p-1 выражением :
, где n=1,2,..p-1
Коэффициент отражения определяется по известным значениям автокорреляционной функции :
, где
Из всех величин только непосредственно зависит от автокорреляционной функции. В разное время предлагалось несколько различных процедур оценки коэффициента отражения, рассмотрим некоторые из них.
1.4.3.1. Геометрический алгоритм.
Ошибки линейного предсказания вперед и назад определяются соответственно следующими выражениями:
Рекурсивные выражения, связывающие ошибки линейного предсказания моделей порядков p и p-1, определяются простой подстановкой и в рекурсивное соотношение для авторегрессионных параметров:
Несложно показать, что коэффициент отражения обладает следующим свойством (является коэффициентом частной корреляции между ошибками линейного предсказания вперед и назад) :
Используя оценки взаимной корреляции и автокорреляции ошибок предсказания вперед и назад, получим :
Таким образом, геометрический алгоритм использует алгоритм Левинсона, в котором вместо обычного коэффициента отражения, вычисляемого по известной автокорреляционной функции, используется его оценка
Окончательный вид выражений геометрического алгоритма :
, где n=1,2,..p-1
,
, где
1.4.3.2. Гармонический алгоритм Берга.
Алгоритм Берга идентичен геометрическому, однако оценка коэффициента отражения находится из других соображений, а именно : при каждом значений параметра p в нем минимизируется арифметическое среднее мощности ошибок линейного предсказания вперед и назад (то есть выборочная дисперсия ошибки предсказания):
Приравнивая производные к нулю, имеем оценку для :
Некоторым обобщением является взвешивание среднего квадрата ошибки предсказания для уменьшения частотного смещения, наблюдаемого при использовании базового метода Берга:
что приводит к следующей оценке :
1.4.4. Оценивание линейного предсказания по методу наименьших квадратов.
Налагая ограничения на авторегрессионные параметры, с тем чтобы они удовлетворяли рекурсивному выражению метода Левинсона, в методе Берга происходит минимизация по одного параметра - коэффициента отражения . Более общий подход состоит в минимизации одновременно по всем коэффициентам линейного предсказания.
Итак, пусть для оценивания авторегрессионных параметров порядка p используются последовательность данных .Оценка линейного предсказания вперед порядка p для отсчета будет иметь форму:
где - коэффициенты линейного предсказания вперед порядка p.
Ошибка линейного предсказания :
В матричном виде это выражение записывается как :
и соотношение для ошибки :
Однако если рассматривать, в котором минимизируется следующая, невзвешенная выборочная дисперсия :
то матрица принимает теплицевый вид (далее ее будем обозначать ).
Нормальные уравнения, минимизирующие средний квадрат ошибки имеют следующий вид:
Элементы эрмитовой матрицы имеют вид корреляционных форм
, где
Таким образом, авторегрессионные параметры могут быть получены в результате решения нормальных уравнений. Рассмотрим алгоритм, который в решении нормальных уравнений учитывает тот факт, что эрмитова матрица получена как произведение двух теплицевых и в результате этого сводит количество вычислений к . При использовании алгоритма Холецкого потребовалось бы операций.
Ошибки линейного предсказания вперед и назад p-ого порядка
Здесь вектор данных , вектор коэффициентов линейного предсказания вперед и вектор линейного предсказания назад определяется следующими выражениями:
, ,
На основе отсчетов измеренных комплексных данных ковариационный метод линейного предсказания позволяет раздельно минимизировать суммы квадратов ошибок линейного предсказания вперед и назад:
,
что приводит к следующим нормальным уравнениям :
,
Введем необходимые для дальнейшего определения :
,
исходя из вида и можно записать :
, ,
где вектор столбцы и даются выражениями :
,
Важными также являются следующие выражения :
Пара векторов-столбцов и определяются из выражений :
Аналогично определяются вектора и , а также и через матрицы и .
Процедура, используемая для обновления порядка вектора линейного предсказания вперед выглядит следующим образом :
, где , в котором
Соответствующий вид имеет процедура обновления порядка для вектора предсказания назад:
, где ,
Векторы и должны удовлетворять следующим рекурсиям обновления порядка:
Используя тот факт, что является эрмитовой матрицей имеем следующие выражения для и :
Введем скалярные множители
Соответствующие рекуррентные выражения для и имеют следующий вид :
Наконец, еще одна рекурсия обновления порядка необходима для вектора :
Обновление временного индекса в векторе коэффициентов линейного предсказания вперед осуществляется в соответствии с выражением :
Выражение для обновления временного индекса у квадрата ошибки линейного предсказания вперед :
Аналогичным образом обновление временного индекса в векторе коэффициентов линейного предсказания назад ведется в соответствии с выражением :
Выражение для обновления временного индекса у квадрата ошибки линейного предсказания назад :
,
где комплексный скаляр удовлетворяет выражениям :
Соответствующие рекурсии по временному индексу для действительных скаляров и даются следующими выражениями:
,
Начальные условия необходимы для того, чтобы начать рекурсивное решение с порядка равного нулю:
, , ,
, ,
,
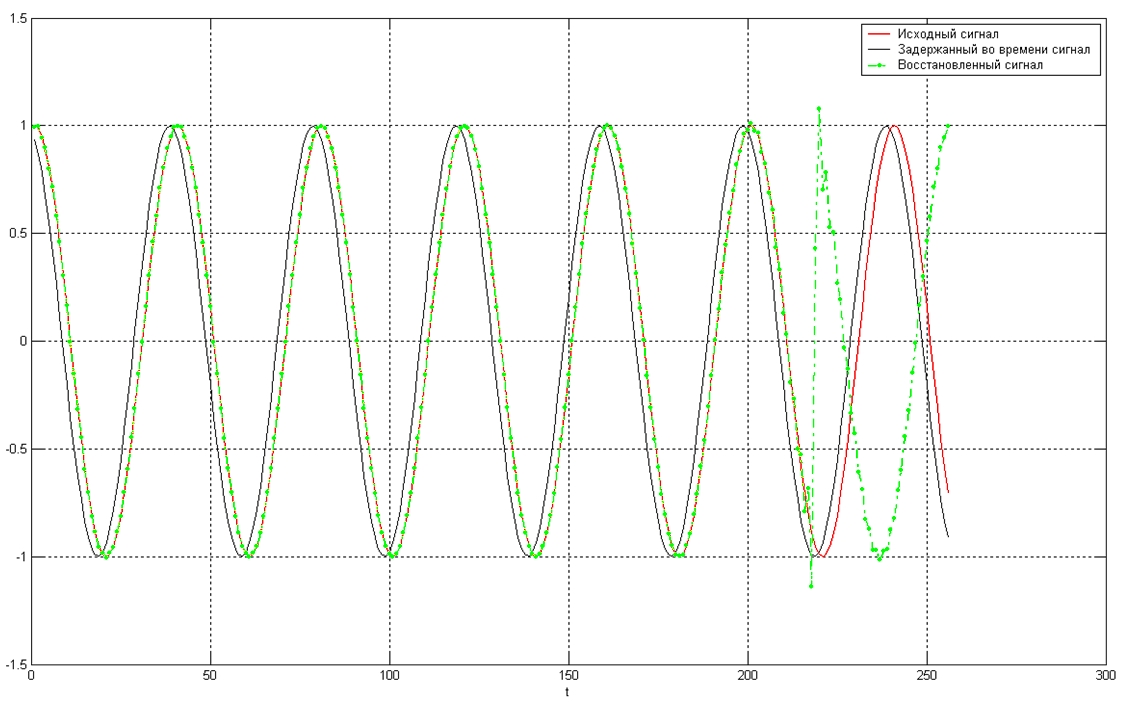
Экспериментальные результаты приведены в соответствующем разделе.
1.4.5. Градиентный адаптивный авторегрессионный метод
1.4.6. Рекурсивный авторегрессионный метод наименьших квадратов
1.5. Спектральное оценивание на основе моделей авторегрессии - скользящего среднего .
Модель авторегресии-скользящего среднего имеет больше степеней свободы, чем авторегрессионная модель, поэтому следует ожидать, что получаемые с ее помощью оценки спектральной плотности мощности будут обладать большими возможностями для передачи формы различных спектров. Основой спектрального оценивания при помощи модели авторегрессии-скользящего среднего является аппроксимация СС-процесса авторегрессионной моделью высокого порядка. Пусть
- системная функция СС(q)-процесса
-системная функция АР-процесса,
эквивалентного этому СС(q)-процессу, то есть
Применим обратное z-преобразование к обеим частям последнего равенства, используя теорему об обратном преобразовании произведения функций, получим:
причем
Таким образом, СС-параметры можно определить по параметрам некоторой эквивалентной авторегрессионной модели посредством решения произвольной подсистемы из q уравнений. Используя АР-оценки высокого порядка можно записать следующую систему уравнений :
В идеальном случае ошибка должна быть равна нулю при всех значениях m, за исключением m=0, однако на практике при использовании конечной записи данных эта ошибка не будет равна нулю, поэтому оценки для CC-параметров должны определятся посредством минимизации дисперсии квадрата ошибки:
Из структуры уравнения для оценок параметров скользящего среднего видно, что эти оценки можно найти, решив соответствующие нормальные уравнения (здесь используется либо «Оценивание корреляционной функции - метод Юла-Уалкера», либо
«Оценивание линейного предсказания по методу наименьших квадратов»)
Общая процедура раздельного оценивания авторегрессионных параметров и параметров скользящего среднего заключается в следующем. Этап первый - определение авторегрессионных параметров по исходным данным, после этого исходную последовательность данных необходимо подвергнуть фильтрации для получения временного ряда приближенно соответствующего некоторому СС-процессу (этап второй). Этот фильтр имеет системную функцию вида :
, где - оценки
авторегрессионных параметров, определенные с помощью метода наименьших квадратов. Системная функция процесса авторегресии-скользящего среднего равна , поэтому
Таким образом, пропуская запись измеренных данных через фильтр с системной функцией , получаем на его выходе аппроксимирующий процесс скользящего среднего. Этап третий : для оценивания СС-параметров применяется процедура, описанная в начале этого раздела. Оценка спектральной плотности мощности АРСС-процесса имеет вид :
, где
- оценка автокорреляции, полученная по фильтрованной последовательности
Экспериментальные результаты приведены в соответствующем разделе.
.
Похожие работы
... частотного диапазона и внешний вид фильтра. То же самое мы видим и для других Частотных диапазонов на плакатах 2 и 3 . Доклад окончен Тема: Модель тракта прослушивания гидроакустических сигналов ОглавлениеВведение Место тракта прослушивания в структуре режима ШП типовой ГАС Формирование канала наблюдения в частотной области 3 Факторы, влияющие на восстановление сигнала 3.1 Перекрытие входных ...
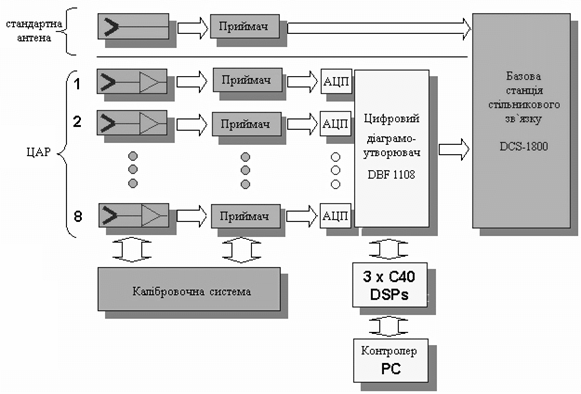
... ідеальних напруг приймальних каналів U, які вільні від ефекту взаємного впливу, вирішується система: , (27) де - вектор реальних напруг приймальних каналів, отриманих після аналого-цифрового перетворювача (АЦП) без проведення корекції. З метою компенсації взаємного впливу, розв’язання системи (12) здійснюється за методом найменших квадратів з мінімізацією функц ...
... на другом или утверждения о реализации идеи человеко-машинного общения. Поэтому исследования в этой области являются весьма актуальными. 3. Разработка программного обеспечения для распознавания команд управления промышленным роботом 3.1 Реализация интерфейса записи и воспроизведения звукового сигнала в операционной системе Microsoft Windows 3.1.1 Основные сведения Звуковые данные хранятся ...
... Кибернетики и Информатики Работа допущена к защите Зав. кафедрой д.т.н., проф. Семушин И.В. _____________________ _____________________ Дипломная работа Адаптивное параметрическое оценивание квадратно-корневыми информационными алгоритмами. Специальность: 01.02 – Прикладная математика. Проект выполнил студент гр. ПМ-52 _______________ Кудрявцев М.Ю. Руководитель: зав. кафедрой МКИ ...


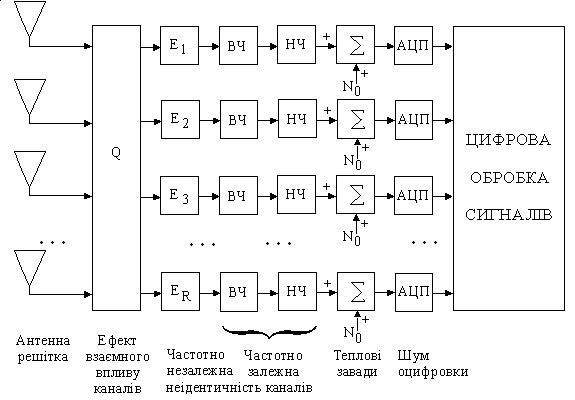
0 комментариев