Навигация
Туннелирование в микроэлектронике
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛАРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОННИКИ
Кафедра химии
Факультет компьютерного проектирования
КУРСОВАЯ РАБОТА
по курсу: «Физико-химические основы микроэлектроники и технологии РЭС и ЭВС»
на тему:
«ТУННЕЛИРОВАНИЕ В МИКРОЭЛЕКТРОНИКЕ »
Выполнил: Приняла:
студент гр. 910204 Забелина И. А.
Шпаковский В.А.
Минск 2001 г.
СОДЕРЖАНИЕ
стр.
1. Туннельный эффект……………………………………………………………………………3
2. ПРОЯВЛЕНИЕ В НЕОДНОРОДНЫХ СТРУКТУРАХ, ИСПОЛЬЗОВАНИЕ В УСТРОЙСТВАХ МИКРОЭЛЕКТРОНИКИ
2.1 Контакт металл-металл…………………………………………………………...…………..5
2.2 Структура металл-диэлектрик-металл………….……………………………………………8
2.3 Токоперенос в тонких плёнках………………………………………………………………10
2.4 Туннельный пробой в p-n-переходе…………………………………………………………12
2.5 Эффекты Джозефсона………………………………………………………………………...13
2.6 Эффект Франца-Келдышева………………………………………………………………….15
3 Туннельный диод…..…………………………………………………………………………17
Литература………………………………………………………………………………………….20
Туннельный эффект
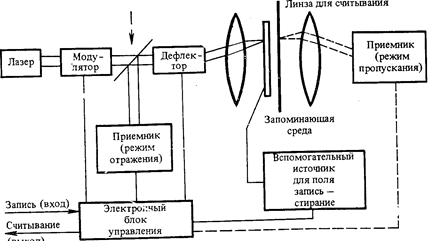
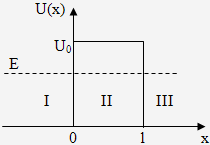
Рассмотрим поведение частицы при прохождении через потенциальный барьер. Пусть частица, движущаяся слева направо, встречает на своём пути потенциальный барьер высоты U0 и ширины l (рис. 1.1). По классическим представлениям движение частицы будет таким:
U(x) - если энергия частицы будет больше высоты барьера (E>U0),
то частица беспрепятственно проходит над барьером;
U0 - если же энергия частицы будет меньше высоты барьера
E (EU0 имеется отличная от ну-
0 l x ля вероятность того, что частица отразится от потенциального
Рис.1.1 Прохождение частицы барьера и полетит обратно. Во-вторых, при EE, волновой вектор k2 является мнимым. Положим его равным ik, где является действительным числом. Тогда волновые функции и приобретут следующий вид:
(1.9)
(1.10)
Так как , то это значит, что имеется вероятность проникновения микрочастицы на некоторую глубину во вторую область. Эта вероятность пропорциональна квадрату модуля волновой функции :
. (1.11)
Наличие этой вероятности делает возможным прохождение микрочастиц сквозь потенциальный барьер конечной толщины l (рис. 1.1). Такое просачивание получило название туннельного эффекта. По формуле (1.11) коэффициент прозрачности такого барьера будет равен:
, (1.12)
где D0 – коэффициент пропорциональности, зависящий от формы барьера. Особенностью туннельного эффекта является то, что при туннельном просачивании сквозь потенциальный барьер энергия микрочастиц не меняется: они покидают барьер с той же энергией, с какой в него входят.
Туннельный эффект играет большую роль в электронных приборах. Он обуславливает протекание таких явлений, как эмиссия электронов под действием сильного поля, прохождение тока через диэлектрические плёнки, пробой p-n перехода; на его основе созданы туннельные диоды, разрабатываются активные плёночные элементы.
2.1 КОНТАКТ МЕТАЛЛ-МЕТАЛЛ
Рассмотрим плотный контакт двух металлов М1 и М2 с разными работами выхода А1 и А2 (рис. 2.1.1).
A1 A2
EF1 n21
n12 EF2
d
M1 M2
Рис. 2.1.1 Энергетическая диаграмма контакта двух металлов в начальный момент времени
Вследствие того, что уровень Ферми EF1 в М1 (уровень Ферми это то значение энергии уровня, выше которого значения энергии электрон принимать не может при Т=0 К) находится выше, чем EF2 в М2, соответствующие работы выхода А1n21 и соответствующие термоэлектронные токи I1>I2. Для этих токов мы можем записать уравнения термоэлектронной эмиссии:
; (2.1.2)
, (2.1.3)
где А* - постоянная Ричардсона; S –площадь контакта.
После выравнивания уровней Ферми поток I2 останется неизменным, а поток I1 уменьшиться, так как для того, чтобы перейти электрону из М1 в М2 кроме преодоления работы выхода А1 ему необходимо преодолеть разность потенциалов в зазоре Vk. Тогда ток I1 станет равным:
. (2.1.4)
При равенстве уровней Ферми двух металлов I1=I2 и результирующий ток через контакт равен нулю. Величину тока, текущего из одного металла в другой в равновесном состоянии, обозначим как Is=I1=I2.
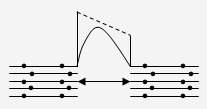
Теперь рассмотрим процессы, происходящие в контакте при пропускании через него внешнего тока. Пусть внешнее поле прикладывается так, что оно складывается с напряжением Vk. Тогда полное напряжение на контакте будет равным V1=Vk+V.
Электронный ток справа налево I2=Is останется неизменным, а ток слева направо уменьшиться, так как высота энергетического барьера для этих электронов увеличится. Уравнение для тока I1 можно записать в виде:
. (2.1.5)
Так как Is=I1 в выражении (2.4), то получим:
. (2.1.6)
Результирующий ток будет направлен справа налево и равен:
. (2.1.7)
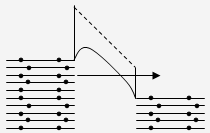
В случае, если внешняя разность потенциалов приложена в обратном направлении, то ток I1 будет больше, чем I2=Is. В этом случае ток I1 равен:
, (2.1.8)
тогда результирующий ток равен:
. (2.1.9)
Если току и напряжению приписывать положительный знак, когда они направлены слева направо, то выражение (2.1.7) для результирующего тока примет такой же вид, как и выражение (2.1.9). Поэтому выражение (2.1.9) называют уравнением вольтамперной характеристики контакта двух металлов.
Из выражения (2.1.9) видно, что контакт металл-металл обладает выпрямляющим действием. При V>0 ток увеличивается по экспоненте, а при V+EF):
, (2.2.3)
где -
высота
потенциального
барьера;
d- ширина
зазора; u-
-
приложенное
напряжение;
m- масса
электрона.
Из полученных
выражений
видно, что
при малых
напряжениях
характеристика
линейна,
а при
увеличении
напряжения
ток резко
возрастает.
Однако реальный
барьер имеет
более сложную
форму. Поэтому
детальный
расчёт
вольт-амперной
характеристики
должен
производиться
с учётом
сил изображения,
различия
эффективных
масс носителей
заряда в металле
и диэлектрике,
а также с
учётом
пространственного
заряда
электронов,
туннелировавших
из металла
в зону
проводимости
диэлектрика,
и электронов,
попавших
на ловушки
в диэлектрике.
Симмонсом
Дж. был
предложен
метод расчёта
туннельного
тока для
барьера
произвольной
формы. Он
ввёл понятие
о барьере
средней
величины.
Этот метод
принципиально
позволяет
вычислить
туннельный
ток с учётом
названных
факторов,
однако при
этом получаются
очень громоздкие
выражения.
Анализ
результатов
расчёта по
методу
Симмонса
показывает,
что при малых
напряжениях
вольтамперная
характеристика
является
линейной,
а при больших
напряжениях
переходит
в экспоненциальную
зависимость.
При дальнейшем
увеличении
напряжения
туннельный
ток ограничивается
пространственным
зарядом
в диэлектрике.
На рис.
2.2.1 показаны
расчётные
вольт-амперные
характеристики
с учётом
пространственного
заряда.
Из рисунка
видно, что
большой
пространственный
заряд может
сильно
ограничивать
туннельный
ток сквозь
слой диэлектрика.
Большое
количество
экспериментальных
работ было
выполнено
по изучению
туннельного
прохождения
электронов
сквозь
тонкие диэлектрические
слои. Плёнки
диэлектриков
обычно создавались
либо термическим
окислением
металлов,
либо распылением
в вакууме.
Исследованию
были подвергнуты
плёнки Al2O3,
Ta2O5,
TiO2, Сu2O,
Сu2S, SiO,
GeO2,
и других
соединений.
Практически
во всех
системах
наблюдалось
качественное
совпадение
экспериментальных
вольт-амперных
характеристик
с расчётными.
В начале
имеет место
линейное
возрастание
тока с
ростом напряжения,
затем оно
переходит
в экспоненциальное
с последующим
замедлением
роста тока.
Последнее
обстоятельство,
как и
предполагалось
при теоретическом
расчёте,
вызвано ловушками
в диэлектрических
слоях. При
соответствующем
подборе
высоты
контактного
барьера,
эффективной
площади
структуры,
эффективной
массы электрона
в диэлектрике
и других
параметров
наблюдается
количественное
совпадение.
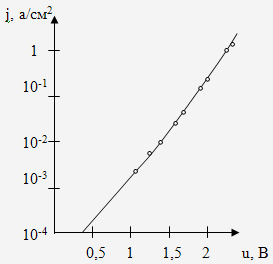
На рис.
2.2.2 приведена
вольт-амперная
характеристика
туннельного
тока сквозь
слой А12О3
толщиной
d=2,3 нм.
Точками показаны
экспериментальные
результаты,
сплошной линией
– расчётные.
Наблюдаемые
в отдельных
случаях количественные
расхождения
в теоритических
и экспериментальных
результах
вызваны, по-видимому,
несовершенством
структуры и
геометрии
плёнок.
j, а/см2
107 1
2
103 3
10-1
10-5
10-9
1 10 100 1000 u, B
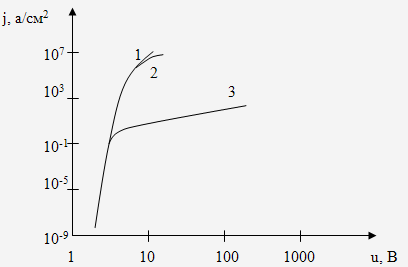
Рис. 2.2.1 Расчётные вольт-амперные характеристики туннельного тока:
1 – без учёта пространственного заряда;
2 – с учётом пространственного заряда подвижных носителей;
3 – с учётом пространственного заряда на ловушках при большой их плотности.
j, а/см2
1
10-1
10-2
10-3
10-4
0,5 1 1,5 2 u, B
Рис. 2.2.2 Вольт-амперная характеристика туннельного тока сквозь плёнку Al2O3. Точки – экспериментальные данные, сплошная линия – расчёт.
Похожие работы
... будут отличаться от сегодняшних и будущих роботов, разве только нейропроцессором. Но и модели поведения нейросистем, несмотря на отсутствие аппаратных реализаций, хорошо проработаны и изучены. Развитие молекулярной нанотехнологии даст возможность тщательно изучить процессы, протекающие внутри клеток организма. Есть большие основания полагать, что точное знание того, как функционируют клетки, ...
... беспредельной ёмкостью памяти, а спецификой механизмов, предохраняющих человеческую память от "переполнения". По быстродействию (скорости записи и воспроизведения информации) машинная память значительно превосходит память человека. Скорость срабатывания элементов, на основе которых строятся современные ЗУ, определяется в конечном счете скоростью протекания электронных процессов, в то время как ...
... хвильової функції : . (1.11) Наявність цієї ймовірності уможливлює проходження мікрочастинок крізь потенційний бар'єр кінцевої товщини l (мал. 1.1). Таке просочування одержало назву тунельного ефекту. По формулі (1.11) коефіцієнт прозорості такого бар'єра буде рівний: , (1.12) де D0 – коефіцієнт пропорційності, що залежить від форми бар'єра. Особливістю тунельного ефекту є те, що при ...
... и 0,18-микронному техпроцессу. Общий принцип работы ячейки флэш-памяти. Рассмотрим простейшую ячейку флэш-памяти на одном n-p-n транзисторе. Ячейки подобного типа чаще всего применялись во flash-памяти с NOR архитектурой, а также в микросхемах EPROM. Поведение транзистора зависит от количества электронов на "плавающем" затворе. "Плавающий" затвор играет ту же роль, что и конденсатор в DRAM, т. ...



0 комментариев