Навигация
П о с т а н о в к а з а д а ч и, р а з р а б о т к а
2.1. П о с т а н о в к а з а д а ч и, р а з р а б о т к а
м а т е м а т и ч е с к о й м о д е л и
Постановка задачи связана с точным описанием исходных данных, условий задачи и целей ее решения. Этап разработки математической постановки называют также этапом формализации задачи. На этом этапе многие из условий задачи, заданные в форме различных словесных описаний, необходимо выразить на точном (формальном) языке математики. Полученная на этапе формализации новая задача называется м а т е м а т и ч е с к о й моделью исходной задачи. В результате инженерная задача приобретает вид формализованной математической задачи.
Рис.3. Поперечное сечение балки с нанесенной сеткой
Нанесем (рис.3) на рассматриваемое тело сетку с квадратными ячейками. Пронумеруем все углы с неизвестными температурами. Температуры в узлах верхней и нижней поверхностей равняются соответственно значениям Тa и Тb , а поэтому на рис.3 не показаны. Разностные уравнения для граничных узлов 6, 9, 11, 13, 20 можно выбрать по рассмотренным выше уравнениям. Система из 20 уравнений баланса энергии запишется следующим образом:
узел 1: T[2]+0,5*(T[7]+Tb)+Bi1*Tc - (2 + Bi1)*T[1] = 0,
где Bi1 = alfa1* x/lamda ;
узел 2: T[1]+T[3]+T[8]+Tb - 4*T[0] = 0 ;
узел 3: T[2]+0,5*(T[9]+Tb)+Bi2*Td - (2+Bi2)*T[3] = 0,
где Bi2 = alfa2* x/lamda ;
узел 4: T[5]+0,5*(T[11]+Tb)+Bi2*Td - (2+Bi2)*T[4] = 0;
узел 5: T[4]+T[6]+T[12]+Tb - 4T[5] = 0 ;
узел 6: T[5]+0,5*(T[13]+Tb) - 2T[6] = 0 ;
узел 7: T[8]+0,5*(T[1]+T[14])+Bi1*Tc - (2+Bi1)*T[7]=0;
узел 8: T[7]+T[9]+T[2]+T[15] - 4*T[8] = 0 ;
узел 9: T[8]+T[16]+0,5*(T[3]+T[10])+Bi2*Td-(3 + Bi2)*T[9]=0;
узел 10: T[17]+0,5*(T[9]+T[11])+Bi2*Td-(2+Bi2)*T[10] = 0 ;
узел 11: T[12]+T[18]+0,5*(T[4]+T[10])+Bi2*Td-(3+Bi2)*T[11]=0 ;
узел 12: T[5]+T[11]+T[13]+T[19] - 4*T[12] = 0 ;
узел 13: T[12]+0,5*(T[6]+T[20]) - 2*T[13] = 0 ;
узел 14: T[15]+0.5*(T[7]+Ta)+Bi1*Tc - (2+Bi1)T[14] = 0;
узел 15: T[8]+T[14]+Ta+T[16] - 4T[15] = 0 ;
узел 16: T[9]+T[15]+Ta+T[17] - 4T[16] = 0 ;
узел 17: T[10]+T[16]+Ta+T[18] - 4T[17] = 0 ; (15)
узел 18: T[11]+T[17]+Ta+T[19] - 4T[18] = 0 ;
узел 19: T[12]+T[16]+T[20]+Ta - 4*T[19] = 0 ;
узел 20: T[19]+0,5*(T[13]+Ta) - 2*T[20] = 0 .
Окончательный вид системы уравнений для нахождения значений температуры в 20 узлах рассматриваемой задачи должен быть выбран в зависимости от метода решения.
В результате применения метода конечных разностей получили 20 алгебраических уравнений для 20 узлов в твердом теле. Эта система уравнений заменяет уравнение(3) в частных производных с соответствующими граничными условиями. Решение полученной системы уравнений позволяет найти распределение температуры в узлах твердого тела.
2.2. В ы б о р м е т о д а ч и с л е н н о г о
р е ш е н и я
Выбор метода решения задачи требует знания соответствующих разделов математики. Выбранный метод должен обеспечить представление вычислительного процесса в виде последовательности элементарных арифметических и логических операций. Если ни один из методов не подходит для решения поставленной задачи, возникает необходимость разработки нового метода.
Задачи, связанные с решением системы линейных алгебраических уравнений, базируются на прямых и итерационных методах. Прямые методы решения основаны на приведении системы уравнений к "треугольному" виду {методы Гаусса, Гаусса - Жордана, Холесского и др.}. Итерационные методы - на выражении неизвестных температур в левые части соответствующих уравнений системы {методы Якоби, Зейделя и др.}.
Коэффициенты при неизвестных температурах в уравнениях образуют разряженную матрицу, т.к. в каждом уравнении для ряда неизвестных они принимают нулевое значение. В этом случае итерационные методы, основанные на последовательном уточнении первоначального приближения для решения, представляют больший интерес по причине высокой вычислительной эффективности.
Анализ достоинств и недостатков методов решения систем линейных уравнений можно найти в специальной литературе [2,7], а применительно к задачам теплообмена [3,4,5].
Рассмотрим в качестве примера итерационный метод Зейделя. В нем из каждого уравнения выражают в явном виде температуру узла, для которого составляется баланс энергии и система уравнений (15) приводится к виду:
1: T[1]=(T[2]+0.5*(T[7]+Tb)+Bi1*Tc)/(2+Bi1);
2: T[2]=(T[1]+T[3]+T[8]+Tb)*0.25;
3: T[3]=(T[2]+0.5*(T[9]+Tb)+Bi2*Td)/(2+Bi2);
4: T[4]=(T[5]+0.5*(T[11]+Tb)+Bi2*Td)/(2+Bi2);
5: T[5]=(T[4]+T[6]+T[12]+Tb)*0.25;
6: T[6]=(T[5]+0.5*(T[13]+Tb))*0.5;
7: T[7]=(T[8]+0.5*(T[1]+T[14])+Bi1*Tc)/(2+Bi1);
8: T[8]=(T[2]+T[7]+T[9]+T[15])*0.25;
9: T[9]=(T[8]+T[16]+0.5*(T[3]+T[10])+Bi2*Td)/(3+Bi2);
10: T[10]=(T[17]+0.5*(T[9]+T[11])+Bi2*Td)/(2+Bi2); (16)
11: T[11]=(T[12]+T[18]+0.5*(T[4]+T[10])+Bi2*Td)/(3+Bi2);
12: T[12]=(T[5]+T[11]+T[13]+T[19])*0.25;
13: T[13]=(T[12]+0.5*(T[6]+T[20]))*0.5;
14: T[14]=(T[15]+0.5*(T[7]+Ta)+Bi1*tc)/(2+Bi1);
15: T[15]=(T[8]+T[14]+T[16]+Ta)*0.25;
16: T[16]=(T[9]+T[15]+T[17]+Ta)*0.25;
17: T[17]=(T[10]+T[16]+T[18]+Ta)*0.25;
18: T[18]=(T[11]+T[17]+T[19]+Ta)*0.25;
19: T[19]=(T[12]+T[18]+T[20]+Ta)*0.25;
20: T[20]=(T[19]+0.5*(T[13]+Ta))*0.5;
При решении все начальные значения температур обычно принимаются равными нулю или значению наименьшей температуры тела, принятой с учетом граничных условий. Использование такого грубого начального приближения приводит к излишним затратам времени на получение решения, Однако при таком подходе значительно экономится время при вводе. Далее проведя вычисления, находим новые значения температур в каждом из 20 узлов. Новое значение каждой температуры сравнивается с предыдущим и если их разность меньше заданного допустимого отклонения, итерационный процесс заканчивается.
Для увеличения скорости решения системы уравнений вычисляемые искомые параметры используются по мере их получения для уточнения значений последующих температур: Т[1] сразу же применяется для вычисления температуры Т[2], полученные значения температур T[1] и Т[2] -для вычисления температуры Т[3] и т.д.
Похожие работы
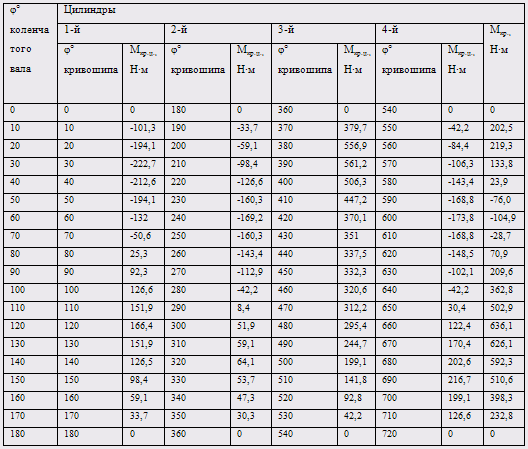
... вала. Таблица 4.3. Результаты расчета крутящего момента По полученным в табл 8. данным Мкр строим график в масштабе Мм= и Мφ=3º в мм. Определяем средний крутящий момент двигателя: – по данным теплового расчета: Мкр.ср.= Мi = Ме / ηм , Н×м ; (116) Мкр.ср.= 220,81 / 0,879 = 251,2 Н×м. – по площади, заключенной под кривой Мкр: Мкр.ср= (F1-F2) ·Мм / ...
... механическим КПД hм =0,95. Среднее эффективное давление цикла (27) МПа Термический КПД цикла (28) ® Геометрические характеристики двигателя Рабочий объем цилиндра (30) ® л Определение диаметра цилиндра и рабочего хода поршня При заданном значении . => Расчет теплообменной поверхности радиатора 1. Исходные данные Мощность двигателя Рe=60Вт Температура воды ...
... изменений Далее будет предложен и рассмотрен вариант усовершенствования системы охлаждения рассматриваемого в данной работе двигателя ЗМЗ-406 автомобилей ГАЗ 2705, 3221 «ГАЗЕЛЬ». Описание целей и элементов доработки системы охлаждения двигателя ЗМЗ-406 по пунктам приведены ниже. Основные элементы системы и режимы работы приведены на рис. 20…24. 1. Вместо вентилятора и гидронасоса с ...
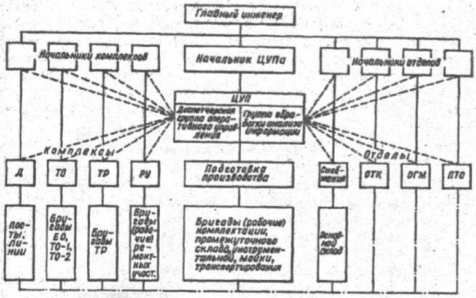
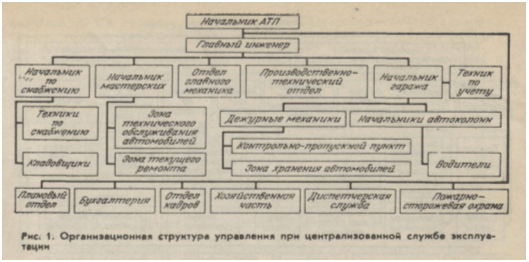
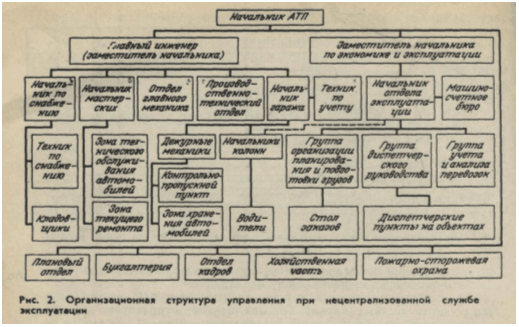
... (ОАСУ) и общегосударственную автоматизированную систему управления (ОГАС). Проектируемое предприятие является по принадлежности предприятием общего пользования, осуществляющее перевозки пассажиров; по организации производственной деятельности – комплексное. Подвижной состав АТП однотипен - 180 автомобилей ПАЗ-3206. Основные характеристики этих автомобилей представлены в таблице 1.1, а их внешний ...


0 комментариев