Навигация
Квантовая физика и квантовая информатика
1.3 Квантовая физика и квантовая информатика
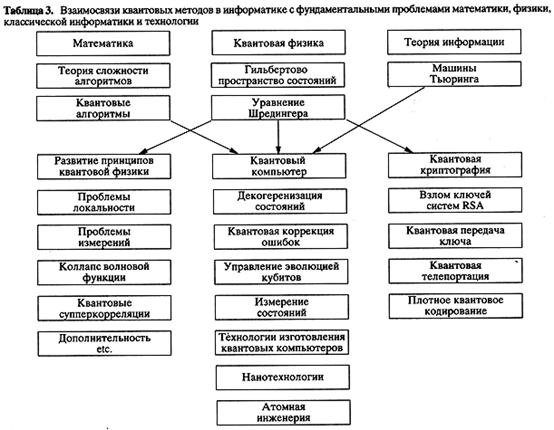
Возможность построения квантовых компьютеров и систем связи подтверждается современными теоретическими и экспериментальными исследованиями. Новая техника XXI в. рождается путем синтеза новых идей в математике, физике, информатике, технологии. Взаимодействие фундаментальных отраслей науки и технологии, рождающее новую технику, показано в таблице 3. Важно подчеркнуть, что в процессе решения задач квантовой информатики происходит развитие и углубление понимания основ квантовой физики, подвергаются новому анализу и экспериментальной проверке основные ее проблемы - локальности (причинности), скрытых параметров, реальности, неопределенности, дополнительности, измерений, коллапса волновой функции.
ГЛАВА 2: Принципы, положенные в основу работы квантовых компьютеров
2.1 Единицы квантовой информации. Кубит.
Любая классическая двухуровневая система, как и квантовая, имеет основное |0ñ и не основное |1ñ базисные состояния. Примером классической двухуровневой системы является известный в микроэлектронике инвертор, осуществляющий операцию НЕ. В зависимости от того заняты ли эти состояния с вероятностями P(0) = 1, P(1) = 0 или P(0) = 0, P(1) = 1, мы имеем булевые логические состояния "0" или "1".
В квантовом случае возникает намного более богатая ситуация. Волновая функция квантовых состояний двухуровневой системы - квантового бита, получившего в дальнейшем название кубита (quantum bit или qubit), может представлять собой суперпозицию базисных состояний (вектор состояния) следующего вида |yñ = a|0ñ + b|1ñ, где a,b - комплексные амплитуды состояний, при этом |a|2 + |b|2 = 1. Помимо вероятностей P(0) = |a|2 и P(1) = |b|2, заполнения базисных состояний |0ñ и |1ñ, состояние кубита характеризуется когерентными или интерференционными слагаемыми в вероятности состояния |yñ, определяемых произведениями комплексных амплитуд ab* и a*b. Состояние квантового бита в отличие от классического может изменяться не только путем изменения вероятностей P(0) и P(1), но и более тонко путем изменения амплитуд состояний a и b, что соответствует поворотам вектора состояния |yñ в так называемом гильбертовом двухмерном пространстве состояний. В этом и состоит принципиальное различие классического и квантового бита.
Двум значениям кубита могут соответствовать, например, основное и возбужденное состояния атома, направления вверх и вниз спина атомного ядра, направление тока в сверхпроводящем кольце, два возможных положения электрона в полупроводнике, различающихся поляризацией фотона или фазой сверхпроводника. Квантовая система может быть макроскопической (сверхпроводники, сверхтекучие жидкости, бозе-газ), отдельной атомной частицей или колебательной модой:
Простейшим случаем двухуровневой квантовой системы является спин ядра атома или электрона I = ½ в постоянном внешнем поле B0: два уровня энергии и состояния соответствуют проекциям спина на направление B0 (рис. 1).
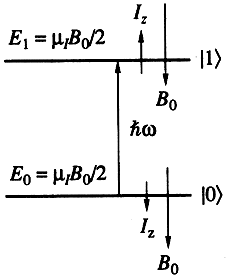
Рис. 1. Состояния спина Iz = ±½ - и его уровни энергии E0,1 = ±miB0/2
во внешнем поле B0 представляют логические состояния кубита |0> и |1>
Два оптических уровня энергии и состояния электрона в ионе также могут быть выбраны в качестве двух состояний кубита (рис. 2).
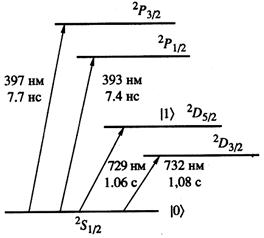
Рис. 2. Состояния иона Са+, соответствующие уровням энергии 2S1/2 (основной) и 2D5/2 (метастабильный) выбраны за логические |0> и |1>. Числа у стрелок показывают длину волны лазера, вызывающего переход, и время жизни иона на соответствующем уровне
2.2 Единицы квантовой информации. Квантовый регистр.
Квантовый регистр устроен почти так же, как и классический. Это цепочка квантовых битов, над которыми можно проводить одно- и двухбитовые логические операции (подобно применению операций НЕ, 2И-НЕ и т.п. в классическом регистре).
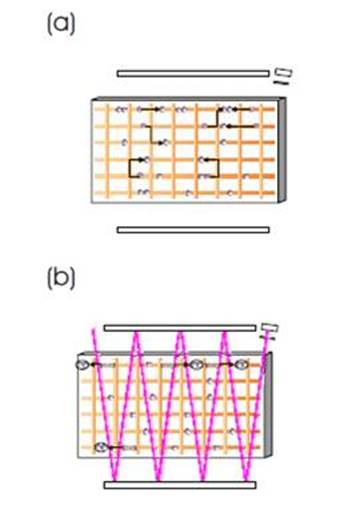
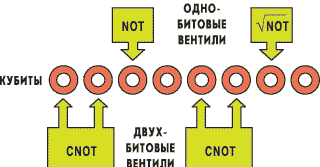 Рис. 3. Квантовый регистр - цепочка квантовых битов. Одно- или двухкубитовые квантовые вентили (NOT 1/2, NOT, CNOT и др.) осуществляют логические операции над кубитами или парами кубитов.
Рис. 3. Квантовый регистр - цепочка квантовых битов. Одно- или двухкубитовые квантовые вентили (NOT 1/2, NOT, CNOT и др.) осуществляют логические операции над кубитами или парами кубитов.
К базовым состояниям квантового регистра, образованного L кубитами, относятся, так же как и в классическом, все возможные последовательности нулей и единиц длиной L. Всего может быть 2L различных комбинаций. Их можно считать записью чисел в двоичной форме от 0 до 2L-1 и обозначать 0,1,2,3, ... 2L-1. Однако эти базовые состояния не исчерпывают всех возможных значений квантового регистра (в отличие от классического), поскольку существуют еще и состояния суперпозиции, задаваемые комплексными амплитудами, связанными условием нормировки. Классического аналога у большинства возможных значений квантового регистра (за исключением базовых) просто не существует. Состояния классического регистра - лишь жалкая тень всего богатства состояний квантового компьютера.
Представим, что на регистр осуществляется внешнее воздействие, например, в часть пространства поданы электрические импульсы или направлены лазерные лучи. Если это классический регистр, импульс, который можно рассматривать как вычислительную операцию, изменит L переменных. Если же это квантовый регистр, то тот же импульс может одновременно преобразовать до 2L переменных. Таким образом, квантовый регистр, в принципе, способен обрабатывать информацию в 2L / L раз быстрее по сравнению со своим классическим аналогом. Отсюда сразу видно, что маленькие квантовые регистры (L<20) могут служить лишь для демонстрации отдельных узлов и принципов работы квантового компьютера, но не принесут большой практической пользы, так как не сумеют обогнать современные ЭВМ, а стоить будут заведомо дороже. В действительности квантовое ускорение обычно значительно меньше, чем приведенная грубая оценка сверху (это связано со сложностью получения большого количества амплитуд и считывания результата), поэтому практически полезный квантовый компьютер должен содержать тысячи кубитов. Но, с другой стороны, понятно, что для достижения действительного ускорения вычислений нет необходимости собирать миллионы квантовых битов. Компьютер с памятью, измеряемой всего лишь в килокубитах, будет в некоторых задачах несоизмеримо быстрее, чем классический суперкомпьютер с терабайтами памяти.
Похожие работы
... , что делает использование нейропроцессоров нерентабельным. Однако аналогичная проблема раньше стояла и перед обычными компьютерами, поэтому следует ожидать, что нейровычислители станут доступнее. 3. Квантовые компьютеры Квантовый компьютер - вычислительное устройство, которое путём выполнения квантовых алгоритмов существенно использует при работе квантовомеханические эффекты, такие как ...
... вычислений - от начала и до конца (кубитом может быть любая квантомеханическая система с двумя выделенными энергетическими уровнями). В результате, для некоторых задач вычислительная мощность когерентных квантовых компьютеров пропорциональна 2N, где N - число кубитов в компьютере. Именно последний тип устройств имеется в виду, когда говорят о квантовых компьютерах. Математические основы ...
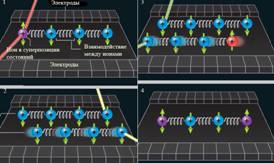
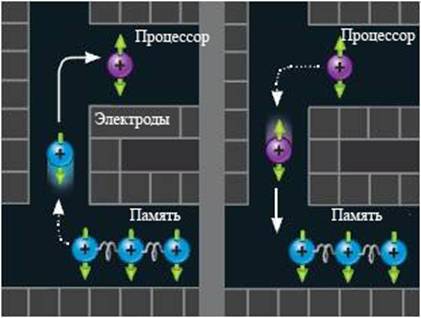
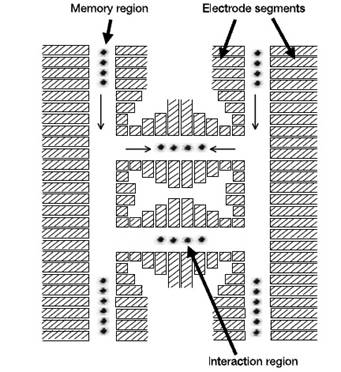
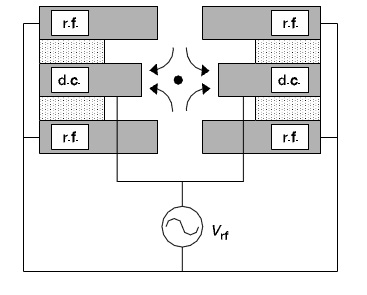
... кубита В данной работе мы рассмотрим примеры схем для большого числа кубитов, реализуемых ионами в ловушках. Архитектура Один из методов для построения квантового компьютера на ловушках для ионов состоит в связывании ионов общим движением. Цепочка ионов электрически подвешена между двумя рядами электродов. Благодаря тому, что ионы заряжены положительно и отталкиваются друг от друга, любое ...
... обучения, yi и yj –выходные сигналы i-го и j-го нейронов. В настоящее время существует множество разнообразных обучающих правил (алгоритмов обучения). Глава IV Может ли компьютер мыслить? 4.1 Реально ли компьютерное мышление? Наконец я подошел к заключительной главе своей работы. В предыдущих главах была изложена сущность построения систем искусственного интеллекта, было рассказано о ...

0 комментариев