Включить в множество ресурсных условий окнченную часть j- й работы к моменту

39. Включить в множество ресурсных условий окнченную часть j- й работы к моменту

времени .

(41) .

40. Зафиксировать минимальное значение срока окончания работ множества .

(42)

41. Выделить из множества . подмножество работ со сроком окончания в момент времени .

(43)

42. Запомнить число освободившихся ресурсов с работ множества .

(44) .

43. Исключить работы множества  из условий других работ, обусловленных технологией проектирования проектов.

(45) .

44. Исключить работы множества  из множества работ, обеспеченных ресурсами, а также из общего списка работ.

(46)

(47)

45. Присоединить оконченные работы в момент времени t2 к работам, каждая из которых окончилась ранее.

(48) .

46. Включить работы множества  в множество оконченных работ .

(49) , где .

47. Определить множество работ, каждая из которых на шаге  может быть включена в ресурсный граф.

(50) , где

48. Пронумеруем работы множества .

, =1, 2, . . . , ,

число работ, включенных в ресурсный граф на шаге  .

49. Определить код работы в ресурсном графе с учетом разбивки работ на части.

(51) .

В ресурсном графе части работ , на каждой из которых число ресурсов постоянно, рассматриваются как самостоятельные работы.

50. Произвести перекодирование условий работ множества .

51. Проверить выполняется ли условие .Если условие выполняется, то принять  и перейти к п. 2;

если нетк п. 52.

52. Конец.

4. Пример.

На разработку, состоящую из 2-х параллельно выполняемых проектов, выделено два различных вида ресурсов по 2 единицы каждого. Исходные данные решения задачи приведены в табл. 1, где код работы  состоит из кода проекта и кода работы в проекте. Первый проект содержит решающий результат с двумя альтернативами: 14,15.

Каждой альтернативе приписана aприорная вероятность: 0,7, 0,3. Требуется в области  определить экстремальный граф, включающий альтернативу 14, вероятность которой равна 0,7. В табл. 2, где код работы с учетом разбивки работ на части, представлен экстремальный ресурсный граф, полученный алгоритмом, основные идеи которого были изложены выше. Более подробно пример рассматривается в [20, 21].

Таблица 1. Исходные данные.

j		Xj	cj			Dj
1	11	0	1	1	2	6
2	12	0	1	2	2	12
3	13	11	1	1	2	8
4	14	13, 12	1	2	2	4
5	15	13, 12	1	1	2	10
6	21	0	1	1	1	4
7	22	0	1	2	1	2
8	23	21	1	1	2	10
9	24	22	1	2	2	4

Таблица 2. Экстремальный ресурсный граф.

				nj
21	21	0	1	1	0	4	4
11	11	0	1	1	0	4	4
11	12	21, 11	1	2	4	1	5
12	13	0	2	1	0	2	2
12	14	13	2	0	2	2	4
12	15	14, 23	2	2	4	5	9
22	22	0	2	1	0	2	2
13	16	12	1	2	5	4	9
24	23	22, 13	2	2	2	2	4
14	17	16, 15	2	2	9	2	11
23	24	16, 21	1	2	9	5	14

Обоснованность задания критерия оптимальности (1) в виде графа следует из теоремы 1.

. Теорема1 Для того чтобы продолжительность выполнения всех работ многопроектной разработки с учетом ресурсов равнялась бы продолжительности критического пути, необходимо и достаточно, чтобы между работами ресурсного графа были установлены связи по ресурсам при соблюдении технологических условий предшествования работ в качестве ограничений.

Доказательство теоремы дается в предпололожении, что чило ресурсов для каждой работы фиксировано.

. Достаточность.Пусть продолжительность критического пути ресурсного графа равна продолжительности выполнения всех работ с.учетом ресурсов. Предположим, что при этом между работами ресурсного графа не установлены связи по ресурсам. В таком случае не для всех цепочек работ, образуемых ресурсными связями, гарантировано   Найдется хотя бы одна такая цепочка, для которой  что противоречит предположению.

. Необходимость. Пусть между работами ресурсного графа установлены связи по ресурсам. Продолжительность самого длинного пути L, который назван критическим, определит продолжительность выполнения всех работ многопроектной разработки.

Получение экстремального графа алгоритмом, включающим пункты , следует из теоремы 2, где под математическим построением сетевой модели будем понимать нахождение графа согласно критерию (1) в области, определяемой ограничениями (2)(5).

Теорема 2. Если все функции , n₂, . . . , ),  вогнуты и аддитивны, то математическое построение сетевой модели многопроектной разработки обеспечивает получение экстремального графа.

Cостояние системы меняется в моменты времени  2, . . . , что соответствует времени обеспечения работ ресурсами. Причем при распределении участвуют все ресурсы, выделенные на выполнение многопроектной разработки, и все работы, свободные в данный момент времени от технологических условий. Для всех значений к,  состояние системыпостоянно. Распределение ресурсов среди работ множества  2, . . . , осуществляется по одной и той же схеме, включающей пункты алгоритма 1для всех  и для всех  2, . . . , В свете сказанного необходимо доказать, что переменные n_{i ,} Z_j обеспечивают максимальное значение функции (1) при фиксированных значениях i, . Зафиксируем значения i, , приняв i=1, . Не теряя общности рассуждений, доказательство теоремы проведем для случая, когда число работ множества A₂, выполняемых 1-м видом ресурсов, равно 2. Для общего случая теорема доказана в работе [19] .

Пронумеруем работы множества А₂ . функция (1) примет вид (52)

(52)  

Пусть в соответствии с условием теоремы

(53) .

(54)  

Рассмотрим матрицу (55).

(55)   

Физически  означает приращение функции (52) за счет того, что на выполнение работы множества А₁ дополнительно назначается одна единица ресурса при условии, что на эту же самую работу уже было назначено  единиц ресурсов.

В силу вогнутости функций  справедливы соотношения (56).

(56)  

С вводом элементов матрицы (55) функция (52) примет вид (57).

(57)  

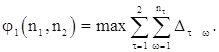
Это следует из (53), если представить

(58)

Преобразуем матрицу  в вектор-строку  p=1, 2, . . ., b₁ так, чтобы элементы вектора образовали вариационный ряд по невозрастанию.

(59)

Элементы ряда (59) обладают тем важным свойством, вытекающим из (56), что если , то найдется такое , для которого . Это свойство имеет место только для вогнутых функций и позволяет предложить конструктивный метод решения задачи. Составим сумму первых J элементов вектора

(60) .

В силу отмеченного выше свойства (59) очевидно, что

(61)

Значение  определяется числом наибольших элементов столбца с номером матрицы , попавших в последовательность .

Таким образом, при распределении ресурсов последовательно двигаясь по наибольшим приращениям функции (52) мы на каждом шаге получаем оптимальный план.

Ресурсы на работу , 1, 2 переходят с работ множества  согласно критерию (52), что обеспечивает получение оптимальной структуры графа. При J=b₁ получаем оптимальное распределение всех ресурсов. В свете сказанного граф (1) является экстремальным.

Список литературы

1 . Х. Ахьюджа. Cетевые методы управления в проектировании и производстве. М.: Наука, 1979.

2. Cборник III-го Bcесоюзного симпозиума по проблемам планирования и управления научными исследованиями и разработками. М.: ЦЭМИ. 1975.

3. Применение пакетов прикладных программ по экономико - математическим методам в АСУ. М.: Статистика, 1980.

4 Глушков В. М. , Михалевич В. C. и др. Управляющий этап // Управляющие системы и машины. Киев: Ин-т кибернетики АН УССР, 1989. N3. С. 5-7.

5. Основные положения по разработке и применению систем сетевого планирования и управления. М. , Экономика. 1974.

6. Костина Л. П. Причины парадоксов при распределении ресурсов на сетях в книге Х. Ахьюджа ? Сетевые методы управления в проектировании и производстве¦ (под ред. В.В Калашникова. М. , 638 c). Деп. организацией п / а А - 1420 МРС

?ТТЭ¦. Сер.0. Вып. 18, Д05134 от 5 августа 1982 г.

7. Fersko-Weis H. Projekt management software // PC Magazine. 1988. November 15. p. 178-226.

8. Fersko-Weis H. High-end proekt managers make the plans // PC magazine 1989 May 16 p. 155-195.

9. С. В. Кохова. Некоторые динамические задачи распределения ресурсов на сетевых графиках с переменными объемами работ // Вестник Московского университета.

сер.15. Вычислительная математика и кибернетика. 1991. N1. C. 48-57.

10. Kouveles P., Lee H.L. Block angular structures and the loading problem in flexible manufakcturing systems // Oper. Res. 1991.V.39. N4. P. 666- 676.

11. Rogers V.R. White K. P. Algebraic, Mathematical Programming, and Notwork Models of the Deterministig Job-shop Scheduling Problem //IEEE Trans. on Systems, Man, and Cybernetics.1991.V. 21. N3. P.693-697.

12. В. И. Левин. Оптимизация расписаний в системах с неопределенными временами обработки // Автоматика и телемеханика. 1995. N2. C. 99-110.

13. В.Н.Калачев, Б. В. Немчинов, В.Е. Кривоножко. Зфдачи планирования в гибких производственных системах // Автоматика и телемеханика. 1995. N6. C. 155-164.

14. П. И. Шарыгин. Оценки приближенного решения одной задачи календарного планирования // Дискретный анализ и исследование операций. Новосибирск: Ин-т математики СО РАН, 1995, т. 2. N1, 57-67.

15. А. В. Кононов. О расписаниях работ на одной машине с длительностями нелинейно зависящими от времени // Дискретный анализ и исследование операций. Новосибирск Ин-т математики СО РАН, 1995, т. 2 N1, 21-35.

16. А. Кофман, Г. Дебазей. Сетевые методы планирования и их применение. М. : Прогресс, 1968

17. Костина Л. П. Математическое построение сетевой модели многотемной разработки. //Теоретический семинар ?Проблемы совершенствования управления научно-техническим прогрессом¦. Московский университет. 1975. С. 253-256.

18. Дымарский Я. С., Прудовский Б. Д. Сталбо А. К. //Вопросы оптимизации в исследовании операций. Труды в/ч 30895. Вып. 99. C. 153-162.

19. Костина Л. П. Опыт создания АСУ проектной организацией на базе методов распределения ресурсов на сетях, обусловленных переменной структурой графа. Деп. организацией п/я А-1420 МРС ?ТТЭ¦, серия 0, вып. 18, Д05135 от 5 августа 1982 г.

20. Костина Л. П. Постановка проблемы оптимального распределения ресурсов на стохастических сетях со сложной пространственно-временной структурой. //Вестник Санкт -Петербургского университета. Сер.1. 1992. Вып. 2 (8). С. 15-19.

21. Костина Л. П. Метод решения задачи оптимального распределения ресурсов на стохастических сетях со сложной пространнственно-временной структурой. //Вестник Санкт-Петербургского университета. Сер. 1. 1992. Вып. 3 (15).