Ķąāčćąöč˙
m (raku organellid) 0.006 s = 6 ms
5 m (raku organellid) 0.006 s = 6 ms
50m (rakud) 0.6s
1 m (organism) 8 aastat
Nagu näeme, on organellis difusioonikiirus sedavõrd suur, et molekul võib umbes 200 korda sekundis läbi organelli difundeeruda. Terve raku mõõtmes on see aga ainult paar koda sekundis. Difusiooniline ainete transport organismi piires on aga lootusetult aeglane. Seetõttu metaboliitide kaugtransport toimubki peamiselt voolamise abil, närvierutus aga liigub elektri-impulsside abil.
Soojusjuhtivus
Tahkes kehas on eriti hästi näha, et soojendades keha ühte osa jõuab soojus varsti jaguneda ühtlaselt üle kogu keha. Soojus nagu difundeeruks laiali. Sama toimub ka gaasides ja see ongi kehade soojusjuhtivus. Kuna soojus on põhimõtteliselt molekulide kineetiline energia, siis selle ‘laialidifundeerumine’ tähendab energia ülekannet põrgetel, kus kiiremini liikuvad molekulid jagavad oma energia teiste molekulidega. Nii kujuneb kehas lõpuks üsna ühtlane molekulide kiiruste jaotus. Et soojusjuhtivuse mehhanism on difusioonile sarnane, siis on ka vastavad valemid sarnased. Näiteks soojuse liikumine läbi varda pikkusega l ja ristlõikepinnaga S on
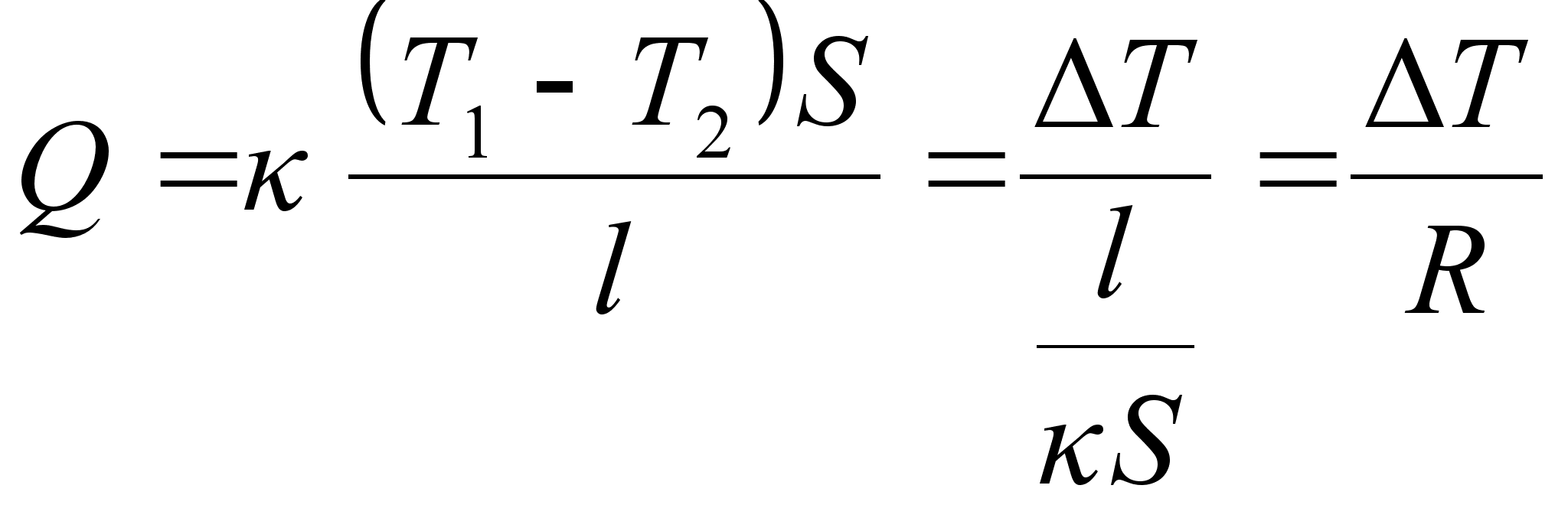
kus kontsentratsioonide vahet asendab temperatuuride vahe ja difusioonikonstanti soojusjuhtivuse konstant
![]()
Soojusjuhtivuse
konstant on difusioonikonstant korrutatud erisoojusega, mis on
tihedus korda massiühiku soojusmahtuvus ![]() .
.
Sisehõõrdumine, viskoossus
Voolamine on molekulide samaaegne ühesuunaline liikumine. Voolamine toimub näiteks torudes rõhkude vahe mõjul. Elusolendites toimub voolamine veresoontes loomadel ja juhtsoontes (ksüleem, floeem) taimedel. Voolamine on peamine viis molekulide transportimiseks pikematel distantsidel kui ühe raku piires. Voolamine võib olla laminaarne ja turbulentne. Laminaarse voolamise puhul vedeliku või gaasikihid torus segunevad ainult difusiooni tõttu, seega vähe, ja kihid, mis alustasid teekonda toru seinte lähedal, on seal toru lõpuni. Molekulid, mis alustasid teekonda toru keskosas jäävad samuti sinna kuni lõpuni. Laminaarne voolamine on tavaline peentes torudes, nagu kapillaarsooned ja taimede juhtsooned. Tubulentsel voolamisel toimub pidev keeriseline liikumine toru sees, selgeid kihte asendavad keerised, milles molekulid liiguvad kord sente lähehedale, kord jälle kaugemale. Turbulentne voolamine on tavaline jämedates torudes. Vaadake näiteks korstnast väljuvat suitsu, aga sarnane keeriselisus on ka vere voolamisel jämedamates veresoontes.
Ka voolamine allub sama tüüpi proportsionaalsele seadusele nagu difusioon ja soojusjuhtivus, ainult siin on liikumapanevaks jõuks rõhkude vahe:
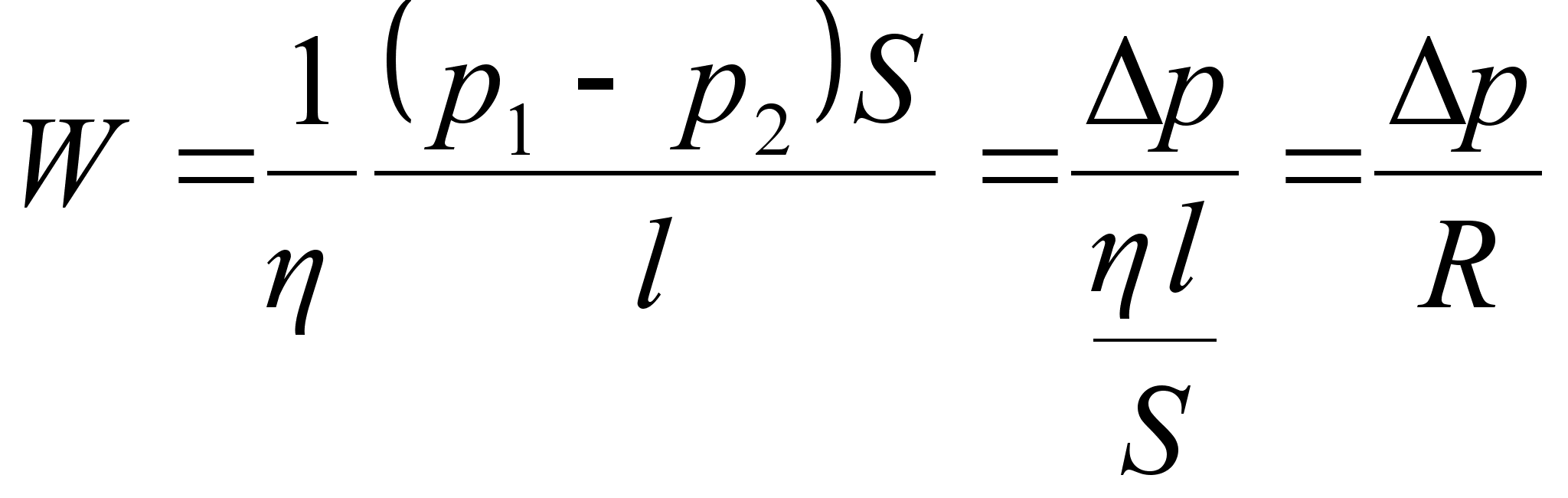
Pange tähele, et voolamise puhul on tavaks võrdetegurit esitada pöördsuurusena, viskoossusena. Mida suurem on viskoossus , seda aeglasem on voolamine sama rõhkude vahe ja sama voolu geomeetria puhul. Vedelike puhul on viskoossus põhjustatud peamiselt molekulidevahelistest sidemetest (tõmbejõududest). Kuna need temperatuuri tõustes nõrgenevad (molekulid liiguvad kiiremini ja kaugenevad üksteisest, keha paisub), siis vedelike viskoossus temperatuuri tõustes väheneb, voolamine kiireneb. Gaaside viskoossus põhineb teisel alusel, kuna nendes molekulidevahelised tõmbejõud ei ole tähtsad. Toru seinte lähedal liikuvad molekulid põrkuvad sageli seintega ja nende edasiliikumine piki toru on takistatud. Soojusliikumine aga pillutab molekule ka toru seintest eemale ja vastupidi, eemal olevaid molekule seinte suunas. Nii jäavad seinte poolt tulevad molekulid tsentri pool liikuvatele jalgu ja pidurdavad neid, aga tsentrist seinte poole liikuvad molekulid kiirendavad seinte lähedal asuvate voolusuunalist likumist. Kujuneb välja keskmine kiiruste profiil, mis on ruuthüperbooli kujuga, kusjuures kõige kiiremini voolavad molekulid toru keskel ja seinte äares on need peaaegu paigal (voolamise mõttes, mitte termilise liikumise mõttes). Kuna gaaside puhul viskoossus on tingitud molekulide difusioonist risti voolu suunaga, on ka viskoossustegur seotud molekulide soojusliikumise keskmise kiirusega ja vaba tee pikkusega:
![]() ,
,
kus on gaasi tihedus. Viskoossus ei sõltu gaasi rõhust, kuna rõhu suurenedes tihedus küll kasvab, kuid vaba tee pikkus proportsionaalselt kahaneb.
Molekulide kiiruste Maxwelli jaotus
Siiani oleme tähelepanu alt välja jätnud asjaolu, et kõik molekulid ei liigu mitte ühesuguse kiirusega. Gaaside rõhu ja temperatuuri vaatlemisel siiski märkisime, et keskmise energia saamiseks tuleb keskmistada molekulide kiiruste ruudud, st. kasutada ruutkeskmist kiirust, difusiooniprotsesside puhul aga oli tarvis kasutada lineaarkeskmist kiirust. Kuivõrd erinevad siiski on molekulide kiirused? Jättes tuletuse kõrvale esitame siin molekulide kiiruste Maxwelli jaotuse:
![]()
Selles valemis ei sisaldu temperatuuri, järelikult u on kiiruse suhteline mõõt mingi teise kiiruse suhtes, mis on temperatuurist sõltuv. Tõepoolest, u on kiiruse suhe kõige tõenäosemasse kiirusesse:
![]() ,
,
kus vt on tõenäoseim kiirus, mis avaldub järgmiselt:
![]() ,
,
kus M on molekulmass. Tõenäoseim, aritmeetiline ja ruutkeskmine kiirus on omavahel järgmistes suhetes:
![]() ;
; ![]() ;
; ![]()
![]() ;
;
Absoluutkiiruse järgi avaldatuna on molekulide kiiruste Maxwelli jaotus järgmine:
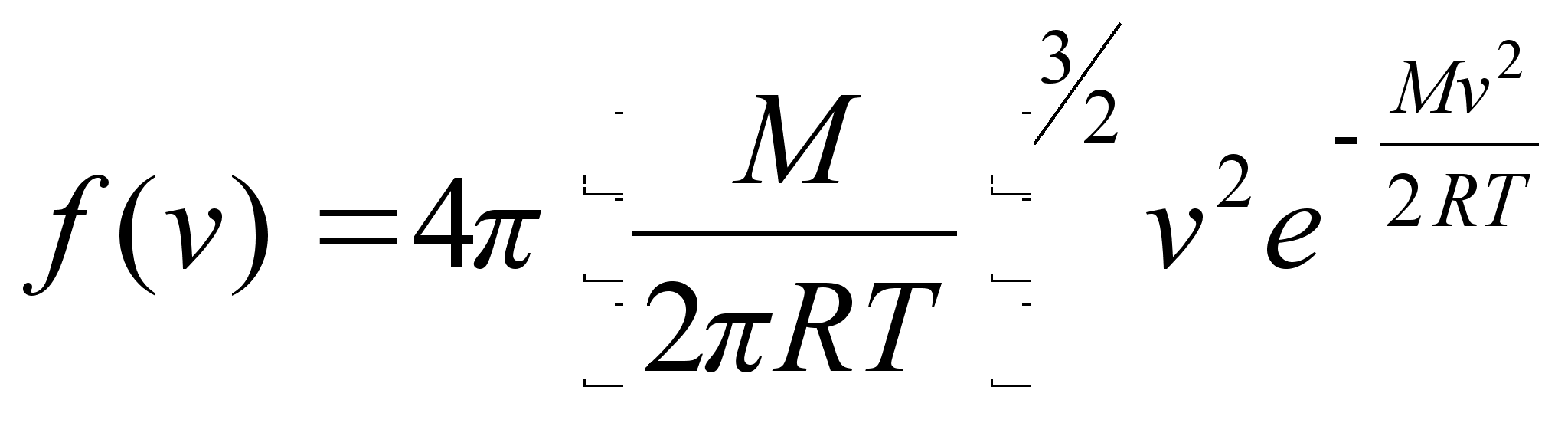
ja seda jaotust kasutatakse järgmiselt. Et leida molekulide suhteline arv, dn/n mille kiirus asub vahemikus v kuni v+dv tuleb arvutada avaldis:
![]() .
.
Maxwelli jaotuse f(v) graafik on esitatud Joonisel. Selle x-teljel on molekulide kiirus m s-1, y-telg aga omab dimensiooni
![]()
See dimensioon võimaldab leida molekulide suhtearvu, mille kiirused asuvad vahemikus v kuni v+dv, kui tulba pindala, mille laius on dv ja kõrgus f(v). Selle kohaselt on mõistlik ainult küsimus, kui suur osa molekulidest omab kiirusi mingis vahemikus, näiteks 400 kuni 410 m s-1. Ebamõistlik on küsimus, kui suur osa molekulidest omab kiirust täpselt 400.000....0 m s-1, sest vastus sellele on: niisuguseid molekule ei ole. Analoogilised on kõik statistilised jaotusfunktsioonid, näiteks kvantide jaotus lainepikkuse järgi ehk kiirguse ‘spekter’. Ka need näitavad tulba d suhtelise pindala kaudu, kui suur osa kvante omab lainepikkusi vahemikus kuni +d.
Vaadates
Maxwelli jaotuse kuju torkab silma, et osa molekulide kiirused on
väiksemad kõige tõenäosemast kiirusest.
Viimane on see kiirus, mille puhul jaotusfunktsioon omab maksimumi.
Matemaatiliselt põhjustab funktsiooni kasvu väikeste
kiiruste juures liige v2. Osa molekule omab kiirusi, mis
ületavad kõige tõenäosema kiiruse. Joonisel
vt-st paremale ja vasemale jäävaid
pindalasid hinnates on neid molekule rohkem, mille kiirus on vt
-st suurem. Sedasama näitab ka see, et aritmeetiline keskmine
kiirus ![]() on kõrgem kui vt. Ruutkeskmine kiirus on
veelgi kõrgem kui aritmeetiline keskmine. Mida suurem on
kiirus, seda vähem on molekule, mille kiirus on sellele lähedal.
Matemaatiliselt põhjustab jaotusfunktsiooni languse suurte v
väartuste korral tegur
on kõrgem kui vt. Ruutkeskmine kiirus on
veelgi kõrgem kui aritmeetiline keskmine. Mida suurem on
kiirus, seda vähem on molekule, mille kiirus on sellele lähedal.
Matemaatiliselt põhjustab jaotusfunktsiooni languse suurte v
väartuste korral tegur
![]() ,
,
mis kahaneb kiiremini kui v2 kasvab. Ometi on siiski olemas molekule, mille kiirus on kahekordne ja isegi kolmekordne tõenäoseim kiirus (vastavalt 800 ja 1200 m s-1 lähedal). Kuna energia on võrdeline kiiruse ruuduga, siis vastavad energiad ületaksid keskmist nelja ja üheksakordselt.
Keemiliste reaktsioonide kulgemisvõime hindamiseks on oluline, kui palju on keskkonnas molekule, mille kiirus ületab mingi vajaliku piiri, näiteks reaktsiooni aktivatsioonienergia (energiabarjääri, mis tuleb ületada, et aatomitevahelised sidemed tekikid). Molekulide suhteline arv, mille energia ületab piiri E avaldub üsna lihtsasti:
![]() .
.
Nagu näha, on molekulide energia võrdlusmõõduks RT, keskmine soojusliikumise energia ühe vabadusastme kohta (toatemperatuuril 2.436 kJ mol-1 ). Suurused
![]()
![]()
![]()
![]()
![]()
näitavad molekulide suhtearvu, mille energia ületab RT vastavalt 1, 2, 3, 4 ja 5 korda. Keemiliste reaktsioonide aktivatsioonienergiad võivad ulatuda kümnetesse kJ mol-1 . Näiteks aktivatsioonienergiat 50 kJ mol-1 suudab toatemperatuuril ületada vaid
![]()
osa koigist molekulidest. Eespool arvutasime, et 1mM kontsentratsiooni juures kohtuvad substraadi molekulid umbes 108 korda sekundis. Kui aga aktivatsioonienergia ületab 50 kJ mol, mis on üsna tavaline biokeemiliste reaktsioonide puhul, siis saavad reaktsiooni astuda ainult
![]() molekuli
sekundis.
molekuli
sekundis.
See ei ole kuigi suur reaktsioonikiirus ja sellest on ilmne, et organismide eksisteerimiseks on hädavajalik reaktsioonide aktivatsioonibarjäari alandamine. See viimane ongi ensüümkatalüüsi tulemus: ensüümid ei muuda reaktsiooni kulgemise energeetilist lõppefekti (alg- ja lõppseisundite energiate vahet), küll aga vähendavad oluliselt vahepealset energiabarjääri, aktivatsioonienergiat.
Aktivatsiooni energiabarjäär vähendab reaktsiooni kulgemise kiirust, ei muuda aga reaktsiooni tasakaalu. Keemilise reaktsiooni tasakaalu määrab reaktsiooni alg- ja lõppseisundite energiate vahe. Olgu meil lihtne juhtum, kus ained A -> B neelates (või vabastades) energiat. Olgu molekulide siseenergia tase vastavalt EA ja EB. Molekulide suhtearv, mille kineetiline energia ületab selle siseenergia taseme EA on
![]()
ja sama energiataseme EB jaoks on
![]()
Logaritmides need avaldised saame
![]()
ja
![]()
SeisunditeA ja B energiate vahe ja vastavat energiat ületavate molekulide arv on seotud järgmiselt:
![]()
Kuigi molekulide siseenergiad EA ja EB võivad sageli olla negatiivsed (oli ju potentsiaalse energia nullnivoo kokkuleppeliselt valitud) ja valemid (??) kaotavd absoluutskaalas mõtte (kineetiline energia ei saa olla negatiivne, kuigi potentsiaalne saab), on seos (???) E jaoks siiski kehtiv. See seos väljendabki keemilises tasakaalus olevate ainete molekulide arvu (kontentratsioonide) suhet. Kui reaktsioonis vabaneb energiat (EB < EA) siis on seisus B molekule rohkem kui seisus A ja lõpp- ja algseisus tasakaalus olevate molekulide arvud suhtuvad logaritmiliselt, nagu valem näitab. Temperatuuri tõus suurendab logaritmi ees olevat kordajat, järelikult ainete B ja A kontsentratsioonide suhe peab siis vähenema, molekulide hulk seisundis A suureneb. Kui reaktsioonis kulub energiat, siis on E negatiivne ja seisundis B on vähem molekule kui seisundis A. Kui E=0, siis on molekulide arvud seisundites A ja B võrdsed. Kui tegu on mitme aine vahelise reaktsiooniga, näit. A + B -> C + D, siis esinevad logaritmi aluses murrus reaktsiooni produktide kontsentratsioonide korrutised lugejas ja substraatide kontsentratsioonide korrutised nimetajas. Seda murdu nimetatakse keemilise reaktsiooni tasakaalukonstandiks.
Nii reaktsiooni tasakaal kui ka kiirus sõltuvad kiirete molekulide osakaalust kogu molekulide arvus. Nägu eespool märgitud, määrab reakstiooni kiiruse nende põrkuvate molekulide arv, mille energia ületab aktivatsioonibarjääri Ea. Kuna nüüd on meil ka avaldis kiirete molekulide avu kohta olemas, võime kirjutada üldvalemi reaktsiooni kiiruskonstandi jaoks:
![]()
Pange tähele, et molekuli kineetiline energia (temperatuur) tuleb reaktsiooni kiiruskonstanti sisse kahel viisil, ühelt poolt tõstes põrke energiat (suurendades kiirete molekulide suhtearvu), teiselt poolt aga suurendab temperatuur põrgete sagedust, sest keskmine kiirus v on võrdeline ruutjuurega kineetiliset energiast, seega ka temperatuurist. Siiski, see viimane annab suhteliselt väikese efekti ja peamine on eksponent-tegur. Seetõttu esitatakse keemiliste reaktsioonide temperatuurisõltuvuste uurimisel need tavaliselt teljestikus logaritm reaktsiooni kiirusest (y-telg) vs. 1/RT (x-telg), millises esituses sõltuvus kujuneb lähedaseks sirgele tõusuga -Ea. See on tuntud kui Arrheniuse graafik.
Molekulide mõõdu ja külgetõmbe arvestamine: reaalne gaas
Nagu selle peatüki alguses tuletasime, on normaalrõhul gaasides molekulide-vaheline kaugus umbes kümme korda suurem nende diameetrist. Seega, gaasi saaks umbes 1000 korda kokku suruda enne kui molekulid pidevalt naabri mõjusfäari satuvad (lineaarmõõt kaugus väheneb kuupjuurega ruumalast!). Molekulide endi ruumala moodustab umbes tuhandiku gaasi koguruumalast normaalrõhul. Isegi vähema kui tuhandekordse ruumala vähendamise ja rõhu tõusu juures hakkab gaaside olekuvõrrand ebatäpseid tulemusi andma, kui molekulide omaruumala ei ole arvesse võetud.
Teiseks, gaaside ideaalne teooria arvestab täiesti elastsete põrgetega, mille juures molekulidevahelisi sidemeid ei teki, vaid molekulide kineetiline energia on jääv. Tegelikkuses on aga molekuide vahel mitte ainult tõukavad jõud (elektronkatete vaheline tõukumine), vaid teatud määral ka tõmbavad jõud. Nende olemasolu tulemusena muutuvad molekulidevahelised põrked sarnaseks kleepuvate piljardikuulide põrgetega: kuulide suurtel kiirustel kleepumisjõud ei ole tähelepandavad, kuid väikeste kiiruste puhul võivad kuulid kokku leepuda. Molekulide vastastikuse toime potentsiaalse energia kõver on esitatud Joonisel. Teatud kaugusel toimivad tõmbejõud, mis vähendavad potentsiaalset energiat, molekulide edasisel lähenemisel aga domineerivad elektronkatete-vahelised tõukejõud ja selles piirkonnas potentsiaalne energia kasvab kiiresti. Kui põrkuva molekuli kineetiline energia on suur, läbib ta potentsiaalse energia miinimumi lohu kiiresti ja põrkub tagasi kõrgenev potentsiaalse energia barjäärilt. Aeglastel molekulidel on aga suurem tõenäosus saada püütud potentsiaalse energia miinimumi lohku, muidugi juhul kui seda lohku läbides osa energiat eemaldub, näiteks samaaegsel põrkel kolmanda molekuliga või infrapunase kvandi kiirguse teel. Neid molekule siduvaid jõude nimetetakse Van der Waalsi jõududeks ja need on looduses väga olulised: tänu nendele moodustuvad vedelikud (vesi), biomembraanid, valgumolekulide kompleksid, need on rakke kooshoidvate jõudude aluseks jne.
Van der Waalsi jõudusid klassifitseeritakse orientatsiooni-, induktsiooni- ja dispersioonijõududeks.
Orientatsioonijõud toimivad polaarsete molekulide püsivate dipoolmomentide vahel. Nende mõju on pöördvõrdeline kauguse kuubiga kuni kuuenda astmega, seega väga lühikestel distantsidel. Püsiv dipoolmoment on näiteks vee molekulil ja see termin tähendab positiivse ja negatiivse laengukeskme mittekokkulangemist, = laeng x distants.
Polarisatsioonijõud on orientatsioonijõududega sarnased, kuid üks kahest molekulist ei peagi püsivat dipoolmomenti omama. Teine, dipoolmomenti omav molekul liigutab oma elektriväljaga esimese molekuli laengukeskmed paigast, nii et need enam kokku ei lange ja tekib indutseeritud dipool. Siin on jõud pöördvõrdeline r6.
Klassifitseeritakse veel nn. hetkelisi dipooljõudusid, mis peaksid sarnased olema hetkeliste sidemete moodustumisele. Näiteks vesinik-sideme tüüpi doonor-aktseptorside, kuid mitte tingimata vesiniku ja hapniku, vaid ka teiste aatomite vahel, võib moodustuda erinevate molekulide aatomite vahel, sidides nii molekule omavahel. Van der Waalsii jõudude suhtelised suurused ja tüübid mõnedes ainetes on antud Tabelis.
Tabel. Van der Waalsi jõud
Aine Dipoolmoment Orientatsiooni Induktsiooni Dispersiooni
[debai] 106 ergxcm6 106 ergxcm6 106 ergxcm6
CO 0.12 0.0034 0.057 67.5
HJ 0.38 0.35 1.68 388
HBr 0.78 6.2 4.05 176
HCl 1.03 18.6 5.4 105
NH3 1.5 84 10 93
H2O 1.84 190 10 75
(siin on jõud antud vanas füüsikalises, nn. Centimeeter-Gramm-Sekund süsteemis, kus
erg on töö, mida teeb jõuf üks düün teepikkusel 1 cm
düün on jõud, mis annab massile 1 g kiirenduse 1 cm s-2).
Paneme tähele, et orientatsioonijõud on suurimad vee molekulide vahel, millel on ka suurim dipoolmoment. Induktsioonijõud on suhteliselt väikesed, kuid dispersioonijõud võivad olla päris tugevad. See näitab, et viimane tüüp jõudusid omab osaliselt keemilise sideme iseloomu.
Molekulide oma-ruumala ja Van der Waalsi jõudude arvestamiseks on gaaside olekuvõrrandisse sisse toodud vastavad parandid:
![]()
Siin konstant b tähistab molekuli omaruumala, mis tuleb koguruumalast lahutada kokkusurumisele alluva ruumala leidmiseks. Liige a/V2 kujutab endast nn. “siserõhku”, mis tuleneb molekule siduvatest jõududest ja arvestatakse olevat pöördvõrdeline ruumala ruuduga. See avaldis peab ligikaudu kirjeldama molekule siduvate jõudude suurenemist nende lähenedes. Kuna molekulidevaheline kaugus kahaneb kuupjuurega ruumalast, siis pöördvõrdelisus ruumala ruuduga tähendab kuuenda astme sõltuvust kaugusest, nii nagu Van der Waalsi jõududel tõepoolest on. Kui ruumala vähenedes siserõhk suureneb, siis järjest vähem jääb välisrõhku p, kuni selleni, et teatud ruumala juures välisrõhk kaob hoopis. Selles seisundis gaas muutub vedelikuks. Matemaailiselt on avaldis (???) kuupvõrrand V suhtes, mis võib omada korraga kuni kolme lahendit. Sellel ei ole aga täielikku füüsikalist sisu, sest gaaside olekuvõrrandisse sissetoodud parandusliikmed on ikkagi ligikaudsed ja empiirilised. Võrrandi tähtsaim väljund on võimalus arvutada, missuguse temperatuuri, ruumala ja rõhu kombinatsiooni juures mingi aine veeldub, s.t.esineb vedelas ja gaasilises faasis korraga. Näitena on Joonisel esitatud CO2 isotermid (P-V sõltuvused konstantse temperatuuri juures). Kõrgemal kui 304 K temperatuuril ei ole võimalik CO2 rõhu abil veeldada (punkt K, 72.9 atm). Rõhku võib tõsta kuitahes kõrgele, kuid vedeliku pinda ei teki, vaid gaas lihtsalt tiheneb üle kogu ruumala. Viirutatud osa parempoolne äär näitab, kuidas veeldumisrõhk väheneb temperatuuri langedes, näiteks 273K juures on see veidi alla 50 atm. Matemaatiliselt on see ala, kus võrrandil (???) on kolm lahendit. Kui veeldumisrõhk on saavutatud ja ruumala edasi vähendada, siis rõhk enam ei muutu ja järjest rohkem gaasi kondenseerub vedelasse olekusse. Sellele protsessile vastavad horisontaal-lõigud Joonisel. Samal ajal annab Van der Waalsi võrrand keeruka kõverjoone kolme ruumala väärtusega, mis vastavad samale rõhule. See tähendab, et tegelikkuses on selles osas lõpmata palju ruumala väärtusi sama rõhu juures, võrrand aga annab neid ainult kolm. Füüsikaline mõte on jällegi viirutatud ala vasakul äärel, mis näitab, kui suure ruumala juures kogu gaas on veeldunud (kõik molekulid lähestikku) ja edasine ruumala vähendamine on seotud rõhu ülikiire tõusuga (vedelik ei ole praktiliselt kokkusurutav). Seega, vaatamata ebatäpsusele veeldumisprotsessi käigu kirjeldamisel, on Van de Waalsi võrrandist palju kasu, sest ta annab korrektsed rõhu, temperatuuri ja ruumala väärtused, mille juures veeldumisprotsess algab ja millal kogu gaas on veeldunud.
VEDELIKUD
Aine läheb vedelasse faasi kui molekulide soojusliikumise kineetiline energia RT on väiksem molekulidevaheliste tõmbejõudude poolt põhjustatud seoste energiast. Vedelikes molekulid asetsevad ligistikku, kuid translatoorne liikumine on siiski võimalik, ilmselt sidemete ebapüsiva iseloomu tõttu, mis võimaldab molekulil osa aega vabalt uidata. Tekivad ka omavahel seotud molekulide suuremad rühmad, doomenid, mis liiguvad teiste samasuguste suhtes. Kuna vedelikus molekule seovad Van der Waalsi jõud ja soojusliikumine püüab neid sidemeid lõhkuda, siis molekulide translatoorse liikumisega seotud nähtused, nagu difusioon ja viskoossus, temperatuurigaseotud nagu keemilised reaktsioonidki: neis nähtustes osalevad ainult suurema energiaga molekulid. Näiteks difusioonikonstant
![]()
Vedeliku eriomaduseks gaasiga võrreldes on pind. Pinnalähedased molekulid on erilises seisundis, sest neile mõjuvad tõmbejõud neljast küljest ja sissepoole, kuid mitte väljapoole. Selle tulemusena tekib resultatiivne sissepoole tõmbav jõud, mis seob pinnalähedased molekulid järgmise kihiga ja ei lase neil ruumi laiali lennata. Pinnalähedased molekulid moodustavad nagu kile, mis püüab kokku tõmbuda ja omandada nii väikese pindala kui võimalik.
Pindpinevus
Pinna püüe kokku tõmbuda on saanud nimeks vedeliku pindpinevus. Pindpinevuse tulemusena püüab vabalt ruumis hõljuv vedelikutilk võtta kera kuju, sest keral on kõige väiksem pinna-ruumi suhe. Pindpinevust iseloomustatakse tõmbejõuga pinna pikkusühiku kohta, nii et piinajoonele mõjuv jõud
![]()
Pindpinevustegurit saab määrata näiteks katsest, mis on kujutatud Joonisel. Siin kaks pinda (ülemine ja alumine) püüavad liikuvat raami tõmmata jõuga, mis on võrdeline liikuva osa pikkusega. Kaudsemalt, kuid täpsemalt saab pindpinevust mäarata näiteks tilga suuruse või kapillaartõusu kaudu. Pindpinevus põhjustabki tilkade, mullide ja vahu moodustumise. Mullide (näit. seebimullide) puhul on siiki veel oluline, et kilet moodustav vedelik oleks piisavalt viskoosne ja ei voolaks kiiresti pindadevahelt ära. See mäarab mulli eluea. Puhta vee pindpinevus on 75 dn cm-1 = 0.075 N m-1, seebiveel on see aga ainult 0.045 N m-1. Temperatuuri tõustes pindpinevus väheneb ja teatud temperatuuril (nn. kriitilises punktis) jõuab nullini. See on seesama temperatuur, mille puhul gaasi kokkusurudes vedeliku pinda enam ei teki.
Kumera pinna all (näiteks muuli sees) tekib lisarõhk, kuna mulli pind püüab väheneda ja mulli kokku suruda. Selle lisarõhu suurus on
![]()
kus r on mulli raadius. Näiteks 1 mm raadiusega õhumullis on lisarõhk
![]() ,
,
1 m raadiusega mullis aga juba 150 kPa, seega üle kahekordse atmosfäärirõhu. Mulli tekkimine vedelikus on äärmiselt raske kui alustada tuleb nanomeetrilisest mõõdust, sest selleks oleks vaja enam kui tuhandekordset atmosfäärirõhku.
KapillaarsusVedeliku pindpinevus on ka kapillaarsusnähtuse aluseks. Ainult et siin tulevad lisaks vedelikumolekulide omavahelistele tõmbejõududel arvesse ka Van der Waalsi tõmbejõud vedeliku ja seda ümbritseva tahke keha (näit. toru seina) vahel. Kui vedelikumolekulide omavaheline tõmme on tunduvalt tugevam kui vedeliku ja seina vahel, siis niisugune vedelik on seina suhtes mittemärgav. Vastupidi, kui vedelikumolekulide omavaheline tõmme on tunduvalt nõrgem kui vedeliku ja seina vahel, siis niisugune vedelik on seina suhtes märgav. Vahepealsed jõudude suhted tähendavad osalist märgamist või mittemärgamist.
Märgava vedeliku seinaäärsed molekulid liibuvad tugevasti seinale ja järgnevad molekulid liiguvad isegi seina mööda kõrgemale, möödudes eelmistest soojusliikumise tõttu. Niiviisi ‘ronib’ vedelik seina mööda üles ja tekib nõgus pind, nn. menisk. Täieliku märgamise korral on meniski ülaserva nurk väga terav, praktiliselt on vedeliku pind seinaga paralleelne. Selle juhu jaoks on kerge arvutada vedeliku kapillaartõusu kõrgust peentes torudes.
Olgu kapillaariraadius r, seega ümbermõõt 2r. Üles-suunatud kapillaarjõud on võrdne ümbermõõdu pikkuse ja pidpinevuskoefitsiendi korrutisega:
![]()
Vedelik tõuseb seni kuni kapillaarjõud ja veesamba raskus tasakaalustavad teineteist:
![]() ,
,
kus r on vedeliku tihedus ja h kapillaartõusu kõrgus. Sellest võrdusest avaldame h:
![]() ,
,
kus g on vedeliku ruumalaühiku kaal ehk erikaal. Kasutades vee jaoks =0.075 N m-1 arvutame vee kapillaartõusu kõrguse hästimärgavates taimede juhtkimpudes sõltuvalt toru raadiusest:
r (m) h (m) vastava kõrgusega taimed
10-4 0.152 heintaimed
10-5 1.52 põõsad
10-6 15.2 puud
Seega, kui veevarustus toimuks ainult kapillaarjõudude toimel, peaks puudel veejuhtetorude (ksüleemitorude) raadius olema alla 1 m. Maailma kõrgeimate puude, sekvoiade kõrgus on 100 m ringis ja neil peaks ksüleemi läbimõõt olema 0.1 m suurusjärgus. Tegelikult on ksüleemitorude raadius suurem, sest nii peente torude takistus oleks liiga suur, et vajalikus koguses vett juhtida (toru takistus viskoossele voolule suurenes pöördvõrdeliselt raadiuse neljanda astmega, seega oleks see sekvoial 1005 = 107 korda suurem kui rohttaimedel (ühe toru kohta). Kuigi jämedama tüve tõttu on puudel rohkem juht-torusid kui roht-taimedel, on nede pikkus suurem ja takistus ikkagi liiga suur. Kõrgete puude veevarustuse juurde tuleme allpool tagasi.
Vedelike auramine
Vedeliku pinnamolekulid moodustavad nagu kile, mis katab allasuvaid molekule. Kõik molekulid, nii pinnal kui sügavuses, on aga soojusliikumises ja omavad Maxwelli kiiruste (Bolzmanni energiate) jaotust. Vastavalt sellele leidub ikka niisuguseid molekule, mille energia ületab molekulide omavahelise seose energia, ja mis seetõttu suudavad end pinnast välja rebida gaasilisse faasi. Nii toimub vedeliku auramine. Auramisel lahkuvad kiiremad ja jäävad vedelikku alles aeglasemad molekulid, mistõttu vdeliku temperatuur langeb.
Aurumissoojust L mõõdetakse soojushulgaga (energiaga), mida tuleb vedeliku massiühikule juurde anda, et see täielikult aurustada konstantsel temperatuuril. Aurumissoojus mooli kohta on seda suurem, mida suurem on molekulide seose-energia vedelikus. Näiteks vee aurumissoojus 100°C juures on ???? kJ mol, 20°C juures aga ???, mis väljendabki vee molekulidevaheliste sidemete energiat mooli kohta. Kõrgemal temperatuuril see kahaneb, sest intensiivsema soojusliikumise tõttu asuvad molekulid vedelikus keskmiselt üksteisest kaugemal (vedelik on paisunud).
Kui vett aurustada vaakumis, siis kõik väljunud molekulid lahkuvad jäädavalt ja vesi aurustub väga kiiresti. Õhus väljunud molekulid põrkuvad õhu molkulidega ja difundeeruvad veepinnast eemale suhteliselt aeglaselt, kusjuures osa neist pidevalt pöördub vette tagasi. Kui veepinna kohal on piiratud ruum, siis täitub see vee molekulidega õhu molekulide vahel kuni tasakaaluseisundini, mil vette tagasipöörduvate ja sealt väljuvate molekulide hulgad on võrdsed. Niisuguses olekus on õhk (gaas) veeauruga küllastatud, ja auru hulk gaasis enam ei suurene. Veeauru osahulka gaasis väljendatakse tavaliselt tema osarõhuga (partsiaalrõhuga), mis on veeauru molekulide poolt seinale avaldatav rõhk. Protsentuaalselt moodustab osarõhk samasuure osa kogurõhust nagu veauru molekulid moodustavad kogu molekulide arvust. Veeauru partsiaalrõhk kasvab temperatuuri tõustes, sest kiiremate molekulide arv, mis suudavad pinnast väljuda, suureneb. Teoreetiliselt peaks veeauru küllastav partsiaalrõhk väljenduma ka Bolzmanni faktori kaudu, kui molekulide suhte arv, mille energia ületab seoseenergia vees. Kuna aga viimane kahaneb temperatuuri tõustes, siis on aururõhu kasv temperatuuriga veidi kiirem kui Bolzmanni faktor. Praktilisek kasutamiseks sobib nn. Magnuse valem:
![]()
Siin valemis rõhk on väljendatud meteoroloogias kasutatavates millibaarides (mb), ühikutes milles nomaalrõhk on 1013 mb, seega 1 mb = 100 Pa. Temperatuur aga on antud juba Celsiuse kraadides ja e aste on asendatud kümne astmega. Näiteks, temperatuuril 20°C annab see valem küllastavaks veeauru rõhuks 23.36 mb, mis moodustab veidi üle 2% normaalrõhust. Seega, toatemperatuuril ei saa õhus olla rohkem kui 2.3% kogu molekulide arvust veeauru molekulid. Siis öeldakse, et suhteline niiskus on 100%, kui veeauru rõhk on küllastav. Suhtelise niiskuse protsent alla saja näitab, kuivõrd on tegelik õhu niiskus väiksem küllastavast sellel temperatuuril. Näiteks, suhteline niiskus R.H.=50% tähendab, et 20°C juures on õhus veeauru partsiaalrõhk 11.68 mb ja 1.15% molekulidest on veeauru molekulid. Seesama suhteline niiskus kõrgemal temperatuuril tähendab aga hoopis suuremat veeauru hulka, sest küllastav niiskus kasvab temperatuuriga ja suhteline niiskus antakse selle suhtes. Temperatuuril 100°C annab valem suhteliseks veeauru rõhuks 1041 mb, mis on võrdne atmosfäärirõhuga (väik erinevus 1013st tuleb valemi ligikaudsusest, teoreetiliselt peaks tulemus olema 1013 mb). See tähendab, et keemistemperatuuril saab küllastava veeauru rõhk võrdseks välisrõhuga. Keevas teekannus koosneb ‘õhk’ vee kohal 100% veeauru molekulidest.
Keemine on nähtus, mis on tingitud vee aurustumisest kõikjalt, nii pinnalt kui sisemusest, sest küllastava veeauru rõhk veidi ületab välisrõhku, vähemalt nii palju, et ka vedeliku poolt avaldadav rõhk ületada. Siiski, vee sisemuses aurumullide moodustumine nõuab tegelikult tunduvalt suuremat rõhku kui välisrõhk, sest moodustuva mulli raadius võib alguses olla väga väike ja mulli pinna poolt avaldatav lisarõhk olla kuni kahekordne atmosfäärirõhk (vt. eespool). Seetõttu on täiesti puhta vee keemaminek takistatud (aurumine toimub ainult pinnalt) isegi temperatuuri tõusul tunduvalt üle 100°C. Niisugust seisundit nimetatakse ülekuumendatud seisundiks. Tarvitseb vaid väikene tolmu või lisandiosakene vette sattuda, kui selle ümber silmapilkselt moodustub mull, mis paisub väga kiiresti ja võib vee nõust välja paisata. Seetõttu tuleb vee keetmiseks ikka lisada kolvi põhja mingeid kehi, mis tekitavad kunstlikke pindu, et neil saaksid mullid moodustuda. Ka vees lahustunud gaasid eralduvad temperatuuri tõustes mullidena ja moodustavad keemistsentreid.
Keemistemperatuur sõltub tugevasti välisrõhust. Mida madalam see on, seda madalamal temperatuuril saavutab veeauru küllastav rõhk välisrõhu väärtuse ja aurumine algab vee sees. Seetõttu kestab muna keetmine kõrgel mäe otsas kauem kui orus. Kui välisrõhk on 23 mb, siis algab keemine juba toatemperatuuril. Seda saab kergesti demonstreerida vaakumpumba kupli all või isegi täites süstla osaliselt veega ja siis kolbi kiiresti väljapoole tõmmates. Kui rõhk on madalam kui 23 mb võib isegi toatemperatuuril olev vesi olla ‘ülekuumennud’, kui keemine ei saa alata mullitsentrite puudumise tõttu. Niisugune olukord tekib näiteks kõrgete puude veejuhtesüsteemis.
Puude veevarustusest
Ülal märkisime, et kõrgete puude latvadeni ei saa vesi tõusta ainult kapillaarsuse teel, sest vastavad kapillaarid oleksid liiga peened ja omaksid liiga suurt takistust, et transpiratsiooniks vajalikku veehulka läbi lasta. Seetõttu mõnedel puudel täidetakse talve jooksul tühjunud juhetsüsteem kevadel juurte rõhuga, millel on osmoodne päritolu. See on mahlavoolamise aeg: tüvesse tehtud august voolab mahl välja, järelikult on tüves suurem rõhk kui väljas. Juurterõhu abil surutakse ksüleemitorud mahla täis kuni lehepungadeni. Varsti aga mahla voolamine lakkab, mis tähendab, et juurte osmoodne rõhk langeb ja ülesurve tüves kaob. August ei voola enam mahla. Vastavalt peaks tüve ksüleemitorud nüüd tühjenema. Lehtedes on aga torustik väga peen ja suudab kapillaarsuse abil hoida veesammast üleval ka mitmekümne meetri kõrgusel. Takistus ei ole siin probleemiks, sest iga üksiku lehe transpiratsioon on aeglane, kapillaaride ülipeen osa on aga suhteliselt lühike. Nii jääbki suhteliselt jämedate ksüleemitorude veesammas ‘rippuma’ lehtede peente kapillaaride külge. Loomulikult kujuneb niisuguses rippuvas veesambas alarõhk, venitus, mis peaks põhjustama aurumullide tekke samba sees ja seega samba katkemise. Ksüleemitorudes on aga vesi väga puhas ja ei sisalda mullitsentreid. Niisuguses ebastabiilses, ülekuumenenud seisundis (madala rõhu tõttu peaks keema, kuid tsentrite puudusel ei kee) ongi puude ksüleemitorud kogu suve. Kui mingil põhjusel veesammas mõnes ksüleemitorus siiski katkeb, siis see toru jäabki tühjaks ja ei täitu enne kui järgmisel kevadel mahlavoolamise ajal.
Veelgi keerulisem on olukord puudes, millel mahlavoolamist ei ole. Neis ei saa tühjenenud ksüleemitoru enam kunagi uuesti täita, vaid tuleb kasvatada uus toru, ja nii, et see kasvamise aegu oleks pidevalt veega täidetud. Selleks tuleb alustada väga tiheda kapillaaridevõrguga alast, milles vesi kapillaarsuse tõttu on kõrgele tõusnud, kuid takistuse tõttu ei saa seda juhtetoruna kasutada. Niisugused on näiteks rakkude seinad. Kasutades eelmise aasta kasvuringi torustiku seinu algmaterjalina saab neid paisutada ja laiendada, samal ajal hoides veega täidetuna. Niimoodi kasvab igal aastal uus ring juhtetorusid, olles kasvu käigus pidevalt tugeva alarõhu all, venitades veesammast laiemaks. Seetõttu ongi puude ksüleemitorude seinad hästi paksud, et vastu panna kõrgele välisrõhule sisemise alarõhu puhul.
Auramise praktilisi rakendusi
Vee ülespumpamine kaevust. Siin on probleem sarnane puude veevarustusega, ainult torustik on jäme ja vesi ei ole vaba keemistsentritest. Ülal asuva imeva pumbaga on võimalik tekitada alarõhk ja veesammas torus tõuseb, kuid ainult kuni selle kõrguseni mil rõhk torus langeb küllastava veeauru rõhuni antud temperatuuril (mõnikümmend mb). Siis hakkab vesi kiiresti aurama ja toru kõrgem osa täitub veeauruga, mitte vedela veega. Teoreetiliselt on seega imeva pumbaga võimalik veesammast tõsta kuni rõhuni 1030-20 = 980 mb = umbes 9.8 m. Praktiliselt töötavad imevad kaevupumbad umbes kuni 8 m sügavuseni. Sügavamatest kaevudest saab vett kätte ainult põhjapumbaga, mis asub kaevus sees. Seetõttu ongi kõigis puurkaevudes spetsiaalsed pumbad, mis lastakse mitmekümne meetri sügavusse kaevutorusse.
Elavhõbebaromeeter. See on sisuliselt samasugune toru nagu kevust vee võtmiseks, ainult siin imetakse elavhõbedat ülespoole. Sammas tõuseb, kuni rõhk samba kohal langeb elavhõbeda auru rõhuni (see on toatemperatuuril väga madal ja ei tule parandina arvsse, seeega rõhk langeb kuni nullini). Välisrõhust sõltuvalt on sellega võrdset rõhku avaldava elavhõbedasamba kõrgus erinev, mille järgi mõõdetaksegi atmosfäärirõhku ja antakse see ühikutes mmHg. Normaalrõhk on 760 mmHg.
Õhuniiskuse mõõtmine, hügromeeter. Selles mõõduriistas kasutatakse valkkehade (juuste, naha) omadust imada õhust vett ja seejuures paisuda. Välisõhu niiskus on tasakaalus valguga ühinenud veega ja valkkeha ruumala on seda suurem mida kõrgem on õhu niiskus. Juukse venimine kantakse kangsüsteemi abil üle osutile. Niisugused hügromeetrid näitavad õhu suhtelist niiskust protsentides küllastavast.
Kaste. Kastepunkt. Kaste tekib, kui õhu temperatuur langeb ja õhus sisalduv veeaur, mis kõrgemal temperatuuril veel ei olnud küllastav, muutub madalamal temperatuuril küllastavaks. Igale õhu absoluutsele veeauru sisaldusele (partsiaalrõhule) vastab kindel kaste tekkimise temperatuur, mida nimetatakse kastepunktiks. Kastepunkti kaudu saab õhu niiskust ka mõõta, näiteks jahutades peeglit kuni see tuhmub tekkivast kastest, mõõtes seejuures peegli temperatuuri. Veeauru patsiaalrõhk leitakse kui küllastav partsiaalrõhk kastepunkti temperatuuril.
Õhuniiskuse mõõtmine, psühromeeter. Aurav keha jahtub vee aurumissoojuse tõttu. Auramine on seda kiirem, mida kuivem on välisõhk. Seega, märg keha jahtub õhutemperatuurist seda rohkem allapoole, mida kuivem on õhk. Keha jahtudes aurumine väheneb (aurumine on määratud vee, mitte õhu temperatuuriga). Keha jahtudes hakkab ümbritsev õhk seda soojendama soojusjuhtivuse tõttu. Teatud temperatuuril tekib tasakaal, kus aurumisest tingitud soojuskadu võrdub õhust juurdetuleva soojusega. See, nn. märja termomeetri temperatuur, on õhutemperatuurist seda madalam, mida kuivem on õhk. Samal ajal sõltub see ka õhutemperatuurist endast. Kasutatakse tabeleid ja valemeid (psühromeetri valemid), mis seovad märja termomeetri temperatuuri õhu suhtelise niiskusega või ka veeauru partsiaalrõhuga erinevatel õhutemperatuuridel. Meteoroloogias kasutatakse õhuniiskuse mõõtmiseks Assmanni psühromeetreid, mis koosnevad kahest termomeetrist, millest üks on kaetud niisutatud batist-tahiga. Vedru- või elektriventilaatori abil kiirendatakse õhuvoolu üle temomeetrite elevhõbereservuaaride, et nii auramine kui ka soojusvahetus välisõhuga mõlemad kiireneksid.
Soome saun. Soome saunas võib õhu temperatuur olla kuni 120-130 °C, ometi on seal võimalik mõnusalt viibida. Seda võimaldab auravate kehade jahtumine vee aurumissoojuse tõttu. Kuumas ja kuivas õhus aurab vesi väga kiiresti ja seetõttu aurav keha jahtub. Kui juba kord higistate, siis ei tundugi 110°C temperatuur enam nii kuumana, sest nii kuumas kuivas õhus on märja termomeetri temperatuur kusagil 40-50°C vahel. Kui aga leili vista, siis õhk niiskub ja otsekohe tundub kuumana, kuigi õhu temperatuur ei pruugigi seejuures tõusta.
Külmutusmasinad. Vedelike aurumissoojuse tähtsamaid rakendusi on külmutusmasinais. Need masinad töötavad sel põhimõttel, et selles ruumiosas, mida soovitakse jahutada, lastakse mingil hästiauruval vedelikul auruda. Aurumine toimub mingis kinnises nõus, mis on varustatud ribidega õhuga hea soojusvahetuse kindlustamiseks. See on nn. jahutusradiaator või aurusti. Aurumise kiirendamiseks pumbatakse gaasilist substantsi kiiresti eemale ja hoitakse aururõhk madalal. Pumba (kompressori) abil surutakse aur kokku ühes teises nõus (kondensaatoris), kus ta kõrge rõhu tõttu veeldub ja veeldumisel eralduva kondensatsioonisoojuse tõttu ka kuumeneb. Ka see nõu on varustatud ribidega, et eralduvat soojust kiiresti õhule edasi anda ja tekkinud vedelik maha jahutada. Jahtunud vedelik lastakse peenikese düüsi kaudu voolata jällegi aurustisse, kus on madal rõhk ja vedelik keema läheb ning aurustub. Niisuguse tsükli tulemusena neeldub pidevalt aurumissoojust aurustis ja eraldub kondensatsioonisoojust kondensaatoris. Kui aurusti on ühes ja kondensaatorteises ruumiosas, siis pumbatakse soojust ühest ruumist teise. Nii töötabki soojuspump, aga ka iga tavaline kümkapp. Külmkapis on aurustiks tavaliselt karbikujuline õõnsate seintega alumiiniumist karp, kus temperatuur on kõige madalam ja saab jäätistki hoida. Kondensaator aga asub külmkapi tagaseinal ja kujutab endast pikka metalltoru, mis on ühendatud hulga peente vasktraatidega, et soojust vahetavat pinda suurendada. Kümkapp pumpab soojust kapi seest väljapoole. Kui kapi uks avada, siis tuba tervikuna soojeneb, sest kuigi aurumis- ja kondensatsioonisoojus teineteist tasakaalustavad, eraldub kompressorist ikkagi lisasoojust detailide hõõrdumise tõttu. Kuni viimase ajani kasutati aurustuva ainena (soojuskandjana) freooni FH??. Kahjuks on see kerge atmosfäärirõhul gaasiline aine, mis õhku sattudes tõuseb stratosfäärikihtidesse ja kahjustab Maad ultraviolettkiirte eest varjavat osoonikihti. Seetõttu ei ole freooni kasutamine külmageneraatorites enam lubatud, vaid see on asendatud millega????.
Lahused, osmoos ja osmoodne rõhk
Lahused on molekulid segud. Lahuse kui segu moodustumise mäaravad lahusti ja lahustunud aine molekulide vahelised tõmbejõud. Kui need on tugevamad kui lahustuva aine molekulide eneste vahel, siis niisugune aine lahustub hästi, vastupidisel juhul, kui tõmbejõud lahustuva aine ja lahusti molekulide vahel on väikesed, lahustub aine halvasti. Väga hea lahustuvusega võivad kaasneda ruumala muutused, näiteks on alkoholi vesilahuse ruumala on väiksem kui komponentide ruumalad eraldi. See näitab, et lahuses on alkoholi ja vee molekulid üksteisele lähemal kui alkoholi molekulid puhtas piirituses. Lahustumisega võivad kaasneda ka energeetilised efektid. Seesama alkoholilahus soojenb vee ja piirituse segunemisel. Alkoholi molekulid satuvad vee molekulide tõmbesfääri ja lähenevad vee molekulidele, süsteemi potentsiaalne enrgia väheneb, kineetiline (termiline) vastavalt suureneb. Naatriumkloriidi lahustumisel vees lahus aga jahtub tugevasti. Keedusoola NaCl kristallide ja jää segu on kasutatud jäätise valmistamisel, sest see jahtub kuni –10°C. Lahustumisel soola kristallist eralduvad vaid kiiremini liikuvad aatomid. Vesilahuses on Na+ ja Cl- ioonid üksteisest polaarsete vee molekulide poolt moodustatud kestaga raldatud ja süsteemi potentsiaalne enrgia on kõrgem kui NaCl kristallis. Samal ajal on aga tõmbejõud Na ja Cl ioonide ja polaarsete vee molekulide vahel küllat tugev, et põhjustada soola head lahustumist. Kui lahus on küllalt lahja, nii et lahustunud aine molekulid üksteist eriti sageli ei kohta ja nedevahelised jõud olulist rolli seega ei mängi, võib lahustunud ainet kujutleda kui gaasi, unustades seda ümbritsevad vee molekulid. Missugune võiks olla “küllat madal” kontsentratsioon? Teame, et õhk käitub küllat lähedaselt ideaalsele gaasile. Õhu kontsentratsioon on 1 mool 22.4 liitris ehk 44.6 millimooli liitris (44.6 mM). Tuhandekordsel ruumala vähendamisel, seega kontsentratsioonil 44.6 M õhu molekulid sattusid pidevasse kokkupuutesse. See oleks äärmus, mille puhul lahust kindlasti gaasina vaadelda ei saa. Praktiliselt ongi nii, et millimolaarsetes kontsentratsioonides oleme õigustatud lahustunud molekule vaatlema ideaalse gaasina, kuid molaarsele lähenedes tekivad juba üsna suured kõrvalekalded. Vastavalt saab ideaalse gaasi võrrandit kasutada rakkude osmoodse rõhu hindamiseks, kui kontsentratsioonid ei ole väga kõrged.
Rakkude ja organellide membraanid koosnevad lipiidide kaksikkihist, mis on veele läbimatu ja ka elektrit (ioone) mittejuhtiv (hügrofoobne, mittemärgav). Vesi läbib membraane selles olevate valk-kehade kaudu, mille sisestruktuur võib olla hügroskoopne (märgav). Mõned valgud on isegi spetsiaalselt mõeldud vee juhtimiseks (akvaporiinid), mõned aga juhivad ioone selektiivselt ja kontrollitult (ioonkanalid). Üldkokkuvõttes vesi siiski läbib rakumembraane küllatki vabalt, kuid paljud ioonid (H+, K+, Na+, dissotsieerunud happejäagid) ja suuremad neutraalsed molekulid (monosahhariidid, disahhariidid) membraani ei läbi. Seega, vee rõhud kahel pool membraani võrdsustuvad, sest juhtival membraanil ei saa tekkida rõhkude erinevust, lahustunud molekulide (solventide) osarõhud aga ei võrdsustu. Tulemusena jääb membraanile mõjuma rõhk, mis on määratud solventide kontsentratsioonide vahega, olles suurem sealpool, kus konsentratsioon on suurem. Lähtudes gaaside seadusest arvutame näiteks, kui suur oleks ühemolaarse lahuse osmoodne rõhk?
Ühemolaarses lahuses on sovendi kontsentratsioon üks mool liitris. Vaadeldes solventi gaasina see tähendab, et ühe mooli ruumala on üks liiter. Normaalrõhul oleks ühe mooli ruumala 22.4 liitrit. Rõhku tuleb suurendada 22.4 korda, et ruumala väheneks ühe liitrini. Seega, ühemolaarne lahus avaldaks 22.4 kordset normaalrõhku. See arvutus on õige normaaltemperatuuril (0°C = 273K). Toatemperatuuril (293K) on see rõhk kõrgem suhtes 293/273=1.073 korda seega on see 24.04 kordne normaalrõhk. Ülaltoodud arutlus ühemolaarse lahuse kohta annab mõnevõrra ülehinnatud rõhu, sest nii kontsentreeritud lahust ei saa enam vaadelda ideaalse gaasina. Madalamate kontsentratsioonide jaoks aga tuleb hinnagut lihtsalt kontsentratsiooniga proportsionaalselt vähendada ja tulemus on seda täpsem, mida madalam on kontsentratsioon. Näiteks kui ühes liitris lahuses on 34 g suhkrut on lahus 100 millimolaarne ja selle osmoodne rõhk oleks toatemperatuuril 2.4 kordne atmosfäärirõhk.
Osmoodne rõhk on rakkudes väga tähtis. Loomsetes rakkudes, millel puudub tugev raku sein, on osmoodse rõhu regulatsioon esmajärgulise tähtsusega. Juba mõneatmosfääriline ülerõhk raku sisemuses, mis vastab 50-100 millimolaarsele solvendi kontsentratsioonile, võib põhjustada vee tungimise rakku ja seega rakkude venimise. Paistetus näiteks on osmoregulatsiooni häirituse tulemus. Raku ruumala piirava seina puudumisel nimelt jätkub vee rakku sisenemine seni kuni solvendi kontsentratsioonid rakus ja väljaspool seda võrdsustuvad. Loomsetes kudeds reguleeritakse osmoodset rõhku solvendi kontsentratsiooni abil rakkudevahelises koevedelikus. Solvendi kontsentratsioonid kahel pool rakumembraani võrdsustatakse või hoitakse nede vahel ainult väike erinevus, nii et vee tungimine rakkudesse oleks kontrolli all.
Taimsete rakkude erinevuseks on nende tugev rakusein, mis koosneb tselluloosist ja pektiinsetest ühenditest. Ka on taimedes rakkudevahelise ruumi vedelikus solvendi kontsentratsioon üsna madal. Rakusein ei luba rakul suuremaks venida, vaatamata sellele, et osmoodne rõhk raku sees on suurem kui väljaspool. Rakk pingestub rõhu all nii nagu õhku täispuhutud paberikott. Sellist taimerakkude siserõhku nimetatakse turgoriks ja see hoiab lehti ja sageli ka varsi kokku kukkumast. Veekao või osmoodse rõhu languse tõttu turgori kaotanud taimede lehed langevad kokku, “närtsivad”. Turgorrõhk võib ulatuda 10-20 atmosfäärini, mis vastab kuni ühemolaarsele solvendi kontsentratsioonile. Soolastes muldades kasvavates taimedes võib see veel kuni kaks korda suurem olla. Peamine ‘osmootikum’, molekulid, mis aitavad osmoodset rõhku luua, on kaaliumi ioonid ja orgaaniliste hapete jäägid (näit. õunhape). Väga kõrgetel solvendi kontsentratsioonidel hakkab kaasa töötama ka valkudega seonduv vesi, mis põhjustab näit kuivade herneste pundumist vees. Seda rõhku mõnikord mõtteliselt eraldatakse ja nimetatakse rõhu maatrikskomponendiks.
Aururõhk kapillaaris ja lahuse kohal
Küllastav aururõhk vedeliku pinna kohal on tasakaaluline seisund veest väljuvate ja difusiooni tõttu sinna tadgasilangevate molekulide voogude vahel. Kui väljumise kiirus sõltub ainult temperatuurist, siis tagasidiffusiooni kiirus sõltub ka pinna kujust. Nõgus veepind ümbritseb ruumi kogu alumisest poolsfääris ja see suurendab tagasidiffusiooni tõenäosust. Efekt on siiski väike kuni pinna kõverusraadius on palju suurem molekuli vaba tee pikkusest, kui suureneb kiiresti pinna kõverusraadiuse vähenedes. Väga väike kõverusraadius peab aga olema vee pinnal kõrgete puude lehtedes olevates kapillaarides, mis hoiavad veesammast kuni mitmekümne meetri kõrgusel. Seega on oodata, et veeauru küllastav rõhk puulehtede rakkude vahelises ruumis on madalam kui küllastav aururõhk tasapinnalise vee kohal. Kapillaaride kohal oleva aururõhu arvutamiseks saab rakendada lihtsat energeetilist tingimust: aururõhk on just niipalju madalam kuipalju kaaluks niisama kõrge tasapinna kohal küllastav veeauru sammas:
![]()
kus pw on aururõhk tasapinnalise vee kohal ja p’w on tegelik aururõhk w on küllastava veeauru tihedus. Asendades sambakõrguse h kapillaartõusu valemist saame
![]()
kus r tähistab vedela vee tihedust. Valem sisaldab veeauru tihedust, mis tuleb leida veeauru rõhust kasutades gaaside seadust. Teame, et kui kogu gaas oleks veeaur, siis ühe mooli ruumala rõhul p ja temperatuuril T oleks
![]()
(unustame hetkeks, et veeaur ei ole ideaalne gaas ja toatemperatuuril ei saa kogu atmosfäar koosneda veeaurust). Kui kogu atmosfäar koosneks veeaurust, siis tema tihedus oleks
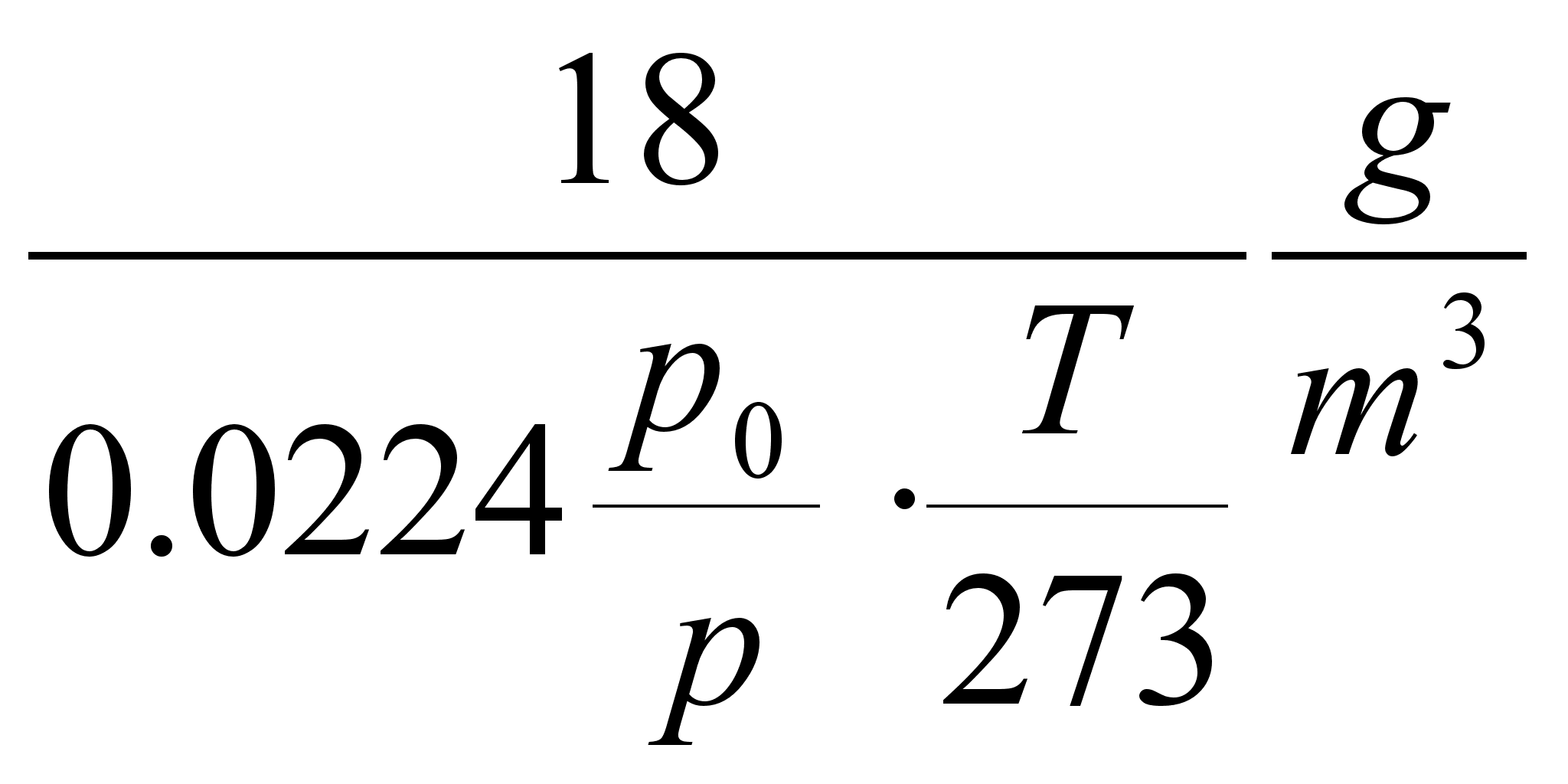
Siiski, mitte kogu atmosfäär ei koosne veeaurust, vaid see osa, mis on määratud veeauru partsiaalrõhu ja kogurõhu suhtega (veeaur on atmosfääris nii hõredalt, et võime teda ikkagi vaadelda ideaalse gaasina). Seega on veeauru tegelik tihedus
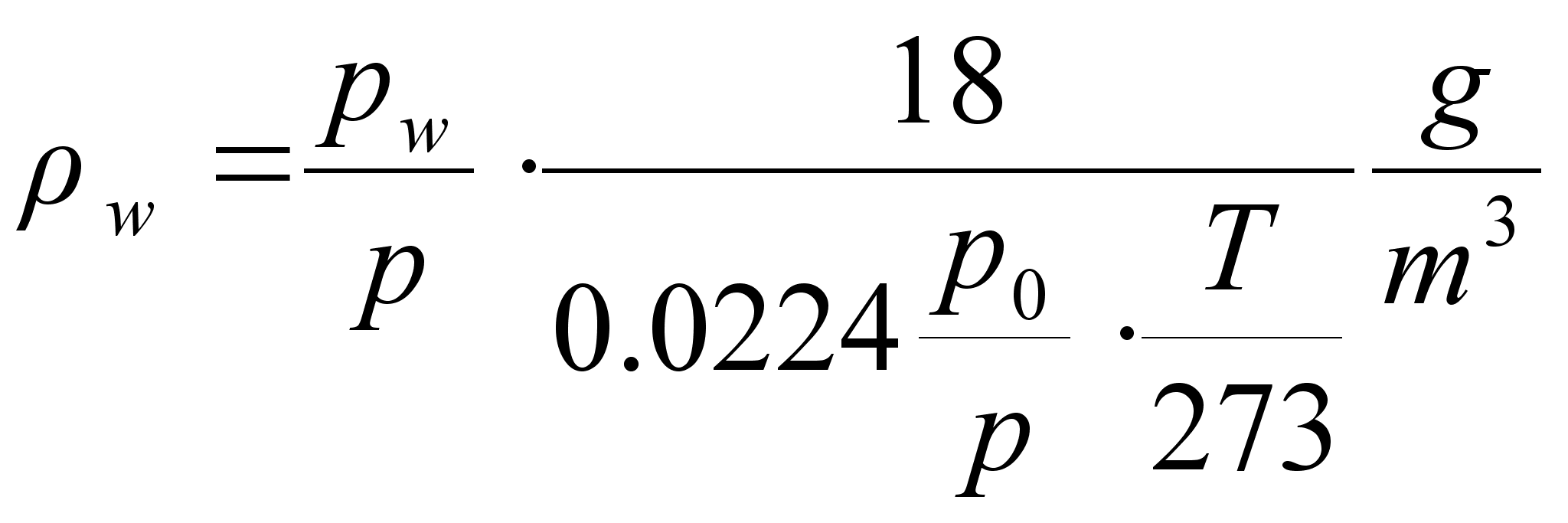
Aururõhk langeb mitte ainult nõgusa pinna (kapillaarse meniski) kohal, vaid on madalam ka lahuse tasapinna kohal võrreldes puhta veega. Suhe on siin lihtne: aururõhk langeb suhteliselt niisama palju kui palju on lahuses vee molekule suhteliselt vähem kui puhtas vees:
![]() ,
,
kus p/p on veeauru rõhu suhteline langus, n’ on lahustunud ja n lahusti molekulide arv ruumalaühikus. Uhemolaarses vesilahuses on ühes liitris Na lahustunud aine molekuli ja ümmarguselt 1000/18=55.6Na lahusti molekuli. Seega ühemolaarse lahuse kohal on aururõhu suhteline langus
![]()
Madalamal kontsentratsioonil on aururõhu langus proportsionaalselt väiksem.
Lahustunud aine kontsentratsiooni suurenedes langeb mitte ainult aururõhk vaid ka lahuse külmumistemperatuur. Ka siin on mõju suhteliselt väike, ligikaudselt
![]()
kus C on lahuse molaarne kontsentratsioon. Kui lahustunud aine dissotsieerub, siis tuleb osakeste arvuks lugeda mõlemad komponendid summana.
TAHKISED
Tahkised ehk tahked kehad on niisugused, mis omavad kindlat kuju ja seega ei voola. Siiski, üleminek voolava ja mittevoolava seisundi vahel on pidev ja mõned kehad siiski voolavad, kuigi väga aeglaselt. Niisuguseid vedlikulaadseid tahkiseid nimetatakse ka amorfseteks kehadeks, sest neil ei ole kristallstruktuuri ja nende kuju on siiski aeglaselt muutuv. Tüüpilisteks näideteks võiks tuua pigi (asfalti) ja klaasi, samuti paljud polümeerid. Tõelised tahkised on seega kristallilise struktuuriga, mis tähendab, et nende omadused (näiteks tugevus või valguse murdumine) sõltuvad suunast, nad on anisotroopsed. Enamik kristallilisi tahkiseid on väga väikeste kristallidega, nii et murdepinnal ei pruugi kristallid alati näha ollla (metallid).
Kristallis on aatomid seotud valents-sidemetega, moodustades seega nagu hiiglaslikke molekule. Sidemed võivad olla kovalentsed või ioon-sidemed, nii nagu molekulidegi puhul. Tüüpiline ioonkristalli näide on keedusool, aga ka teised leeleismetallide soolad (kuupvõre). Ühesugustest aatomitest moodustuvad kristallid kovalentsete sidemete abil. Näiteks toome teemanti, milles süsiniku sp4 hübridiseerunud orbitaalid on seostunud naabersüsiniku orbitaalidega.
Kristallilised ained on elastsed. See tähendab, et kui neile rakendada jõudu, siis aatomid veidi nihkuvad oma tavalistelt, stabiilsetelt asukohtadelt, kuid püüavad siiski stabiilsesse seisundisse tagasi pöörduda. Makroskoopiliselt väljendub see keha (näiteks metallvedru) paindumises. Paindumisel vedru üks pool surutakse kokku, teine aga venitatakse välja. Deformatsiooni suurus (nihke suurus) on võrdeline rakendatava jõuga ja vastupidi, vedru poolt avaldatav jõud on võrdeline kokkusurumise (venituse) suurusega. Kui deformatsioon ületab teatava piirsuuruse, siis toimuvad kristallide tasapindade omavahelised nihked ja aatomid ei naase enam endistesse asukohtadesse, vaid moodustavad sidemed teiste naabritega. Niisugune deformatsioon on jääv ehk plastiline deformatsioon. Mõned metallid, nagu seatina, on vähe-elastsed ja alluvad kergesti plastilisele deformatsioonile, teised, nagu teras, on väga elastsed ja võivad plastiliselt üldse mitte deformeeruda, ennem murdudes.
Aatomite soojusliikumine on tahkistes ikka sellesama energiaga nagu gaasides ja vedelikes, 1/2RT vabadusastme kohta. Vabadusastmete arv on aga kristallilises kehas üsna keeruliselt määratav suurus ja seetõttu on tahkiste mool-soojusmahtuvus (soojushulk, mis kulub ühe mooli aine temperatuuri tõstmiseks ühe kraadi võrra) raskesti ennustatav. Kindel on, et peaaegu ainuke liikumisvorm on võnkumine. Kõik aatomid võnguvad, kord lähenedes kord kaugenedes, mingi keskmise kauguse ümber. Temperatuuri tõustes võnke-energia, seega võnke-amplituud, suureneb. Amplituud saab aga suureneda põhiliselt sel viisil, et maksimaalne kaugus suureneb, samal ajal kui minimaalne kaugus palju ei vähene. See tähendab, et aatomitevaheline keskmine kaugus suureneb. Makroskoopiliselt väljendub selles tahkiste soojuspaisumine: temperatuuri tõustes tahke keha mõõdud suurenevad. Soojuspaisumine on suhteliselt väike, protsendi murdosa kraadi kohta, kuid muutub oluliseks kui temperatuur tõuseb palju. Näiteks, klaasnõud võivad puruneda, kui neid kuumutada ebaühtlaselt, nii et mõni koht paisub rohkem ja mõni vähem.
Tahkumine ja sulamine
Vedeliku tahkumine tähendab aatomite (molekulide) vaheliste sidemet tugevnemist sedavõrd, et aatomite asukohad üksteise suhtes fikseeruvad. Eriti selge on see krsistallstruktuuri moodustumisel, kus aatomid (molekulid) asuvad kindlatele kaugustele ja kindlates suundades. Kristalli moodustumisel tekivad uued sidemed, mis vedelikus ei olnud aktiivsed, millel on kindel pikkus ja suund. Nende sidemete moodustumisel aatomid üldiselt veelgi lähenevad teineteisele ja vabaneb sidemete moodustumise energia (aatomite lähenemisel vabaneb tõmbejõudude potentsiaalne energia). Seega, tavaliselt on tahkes olekus aine ruumala väiksem kui vedelas ja tahkumisel vabaneb teatud hulk energiat, sarnaselt, nagu energiat vabanes auru (gaasi) kondenseerumisel vedelikuks. Tahkise sulamisel aga vastupidi, neeldub energiat, et lõhkuda kristalli-sidemeid. Niisuguse tahkumis/sulamissoojuse olemasolu on hästi nähtav tahkete kehade soojendamisel kindla võimsusega, näiteks küttes neid kindla voolutugevuse ja pingega elektrienergia abil (võimsus = pinge x voolutugevus). Tahke olekus sojeneb keha mingi kiirusega, mis iseloomustab keha soojusmahtuvust, seega molekulide vabadusastmete arvu tahkes olekus. Sulamistemperatuuri saabudes temperatuuri edasine tõus lakkab ja sama temperatuuri juures hakkab suurenema vedeliku hulk ja vähenema tahkise hulk. Sulamistemperatuuril kogu juurdeantud soojusenergia kulub kristalli-sidemete lõhkumiseks, keha temperatuur ei tõuse. Niisugune konstantsel temperatuuril sulamine on iseloomulik just kristallilistele, tõelistele tahkistele. Amorfsed tahkised, mis tegelikult on väga viskoossed vedelikud, pehmenevad ja muutuvad voolavaks aeglaselt üle laia temperatuurivahemiku, kusjuures ekstra sulamis-soojust on nende puhul peaaegu võimatu märgata: temperatuur tõuseb ühtlase kiirusega kui juurdeantav võimsus on konstantne.
Sulamissoojust saabki mäarata soojushulga järgi, mis tuleb konstantsel temperatuuril lisada, et kogu tahkis sulatada. Jää sulamissoojus on 80 kcal kg-1 (1.44 kcal mol-1 = 6.02 kJ mol-1), mis on tunduvalt vähem kui vee aurumissoojus (550 kcal kg-1 = 9.9 kcal mol-1 = 41.4 kJ mol-1). Jää sulamissoojus on tahkiste hulgas üks suuremaid, näiteks elavhõbedal on see ainult 2.75 kcal kg-1. Isegi arvestades, et elavhõbeda aatomkaal on 80, tuleb tema mool-sulamissoojuseks 220 cal mol-1 , mis on siiski 6.5 korda väiksem kui veel. See vahe on põhjustatud suhteliselt tugevatest sidemetest, mis jääkristallis molekule koos hoiavad.
Peale suhteliselt suure sulamissoojuse on veel veel teisigi omapärasid. Enamik vedelikke rõhu suurenedes tahkestuvad, eriti kui temperatuur on tahketumistemperatuuri lähedal. Jää aga vastupidi, sulab rõhu suurenedes. See tuleb anomaalsest ruumalamuutusest tahkestumisel: nimelt vee ruumala tahkestudes suureneb, vastupidiselt enamusele ainetele (niisamasugused erandid on veel vismut ja antimon. Null kraadi juures on jää ruumala umbes 9% suurem kui vee ruumala. See põhjustabki, et rõhu suurenedes külmumistäpp langeb umbes 1° 130 atm kohta. Uisutaldade all võib rõhk ulatuda kuni 80 kG/(0.2 cm x 10 cm)=40 kG/cm-2. Null kraadi lähedal aitab see jääd sulatada ja muudab sõidu libedamaks, lisaks hõõrdumisel tekkivale soojusele, mis ka jääd sulatab.
Sulamistemperatuur sõltub ka kristallvõre puhtusest. Lisandid langetavad sulamistemperatuuri, seetõttu on metallide sulamite sulamistemperatuur tavaliselt madalam kui puhastel komponentidel. Näiteks seatina ja inglistina segu, mida kasutatakse jootmisel, sulab palju madalamal temperatuuril kui komponendid eraldi võetuna.
Vee omapärad
Kuna vesi/jää on bioloogiliselt tähtsaim keskkond, peatume sellel eraldi. Nagu öeldud, on jää sulamissoojus tunduvalt suurem kui näiteks metallidel, mis näitab kristallsideme suhtelist tugevust. Teiseks, jääkristall on suurem kui sama mass vett, mis näitab, et jääd moodustavad sidemed on pikemad kui vett koos hoidvad sidemed. Vahe pole küll suur, kuupjuur 1.09 = 1.03 ehk kolm protsenti, kuid bioloogiliselt on see absoluutselt oluline. Kui jää oleks vest raskem ja vajuks põhja, külmuksid veekogud põhjani ja talvine vee-elu oleks võimatu või vähemalt nõuaks veelgi radikaalsemaid kohastumisi.
Teame, et vees hoiavad molekule lähestikku Van der Waalsi orientatsioonijõud, mis põhinevad vee molekulide polaarsusel. Ilmselt moodustuvad jääs uued sidemed, mis hoiavad molekule veelgi kõvemini koos, kuid seejuures tõukavad nad omavahel kaugemale kui nad on vees. Ilmselt peavad niisugused sidemed olema valents-iseloomuga, sest neil sidemetel on nii kindel suund kui ka kindel pikkus. Need ongi meile juba tuntud vesiniksidemed, ehk doonor-aktseptorsidemed, mis moodustuvad vee hapniku vaba elektronpaari abil mõne teise molekuli vesinikuaatomi tühja orbitaaliga, millelt elektron on ajutiselt lahkunud hapniku elektronegatiivsuse tõttu. Kokku võib üks vee molekul olla seotud teistega kuni nelja vesiniksideme kaudu. Kaks nendest moodustavad tema enese hapniku kaks elektronpaari (hübridiseerunud 2s- ja 2p-paarid), kaks aga on doneerinud teiste molekulide hapnikud esimese molekuli vesinikele. Huvitav on seejuures see, et kõik vesiniksidemed ei ole ühepikkused, vaid sõltuvad suunast kristallvõres (2.76 ja 1.77 A, sõltuvalt suunast). Niisugused mitmekordsed sidemed kõigi molekulide vahel hoiavadki jää kristallstruktuuri.
Jää sulamisel vesiniksidemed katkevad, selleks vajalik energia ongi sulamissoojus. Ometi ei katke 0°C juures kohe kõik vesiniksidemeid vaid vees säilivad veel suhteliselt suured, mõne kuni mõnekümne molekuli suurused klasterid (mikrokristallid). Samal ajal ei ole need klasterid permanentsed vaid pidevalt ümberorganiseeruvad, ühtede sidemete katkedes ja teiste tekkides. Nende jää-sarnaste klasterite olemasolu tõttu ei ole vee ruumala minimaalne 0° juures, vaid temperatuuri tõustes kahaneb, sest klasterite arv ja ruumala vähenevad. Ruumala saavutab miinimumi (tihedus maksimumi) 4°C juures. Sel temperatuuril ei ole klasterid mitte täielikult kadunud, vaid on saabunud tasakaal kahe protsessi vahel, millest esimene on ruumala vähenemine vesiniksidemete arvu vähenemise tõttu, teine aga ruumala suurenemine molekulide võnkeliikumise amplituudi suurenemise tõttu. Kõrgematel temperatuuridel kui 4°C on ruumala suurenemine ülekaalus, kuidi vesiniksidemeid säilib kuni keemistemperatuurini.
Isolaatorid ja elektrijuhid.
Osa tahkeid aineid ei juhi elektrit. See tähendab, et elektronid on aatomitega (molekulidega) seotud ja ei ole võimelised ühelt aatomilt teisele liikuma. See kehtib ka kristallilise struktuuriga isolaatorite kohta, nagu näiteks teemant.
Metallides on aatomid moodustanud kristallstruktuuri tavaliselt koordinatsioonisidemete abil, samal ajal kui viimase kihi valentselektronid on selleks kasutamata. Need elektronid võivad ema-aatomist lahkuda ja moodustada kristallvõres ühise elektronpilve, nn. elektrongaasi. Elektrongaasi olemasolu näiteks suurendab metallide soojusmahtuvust (lisaenergia 3/2RT kulub elektrongaasi soojendamiseks). Tähtsam aga on, et elektrongaas põhjustab metallide küllaltki hea elektrijuhtivuse. Vastasmõju elektronide ja kristallvõre vahel põhjustab aga elektritakistuse olemasolu. Väga madalatel temperatuuridel (absoluutse nulli lähedal) ulatub iga elektroni lainefunktsioon läbi kogu metalli ruumala ja vastasmõju kristallvõrega kaob. Niisugune seisund on ülijuhtivus. Elektrisignaal levib läbi metalljuhtme valguse kiirusega, nii kiiresti nagu ühest otsast juurdetulnud elektronide elektriväli levib. Samal ajal ei liigu elektronid ise mitte nii kiiresti. Näiteks voolutugevusel üks amper liigub läbi juhtme laeng üks kulon sekundis. Üks kulon on 96500 korda väiksem kui Avogadro arv, seega liigub läbi juhtme ristlõike sekundis 1/96500 mooli elektrone. Kui vaskjuhtme diameeter on 2 mm, siis üks mool vaske (63.5g) moodustab juhtme pikkuse 254 cm. Teades, et sekundis läbib juhet 1/96500 mooli elektrone, leiame, et need liiguvad edasi pikkuse 254/96500 = 0.0026 cm = 0.026 mm võrra sekundis.
BIOENRGEETIKA ALUSED
Rakkude energiaallikaks on elektronide liikumine molekulidelt, millel orbitaalid on kõrgema energiaga (tuumadest kaugemal) molekulidele, millel orbitaalid on madalama energiaga (tuumadele lähemal). Elektroni ülekandereaktsioone nimetatakse redoks-reaktsioonideks ja need on organismi primaarseks energia-allikaks. Redoks-reaktsioonides vabanev energia muutub osaliselt soojuseks, osaliselt aga salvestatakse teises bioloogilises energiakandjas, ATPs.
Adenosiin-trifosfaadi (ATP) molekulis on kolm ortofosfaadirühma järjestikku ühendatud hapniku molekuli kaudu. Dissotsieerunud OH rühmad ja reastikku paigutud hapniku aatomid moodustavad rea ligistikku asetsevaid negatiivseid laenguid, mis tõukuvad, kuid ei saa kaugeneda hapniku-sideme tõttu. ATP molekul on energeetiliselt sarnane vedru-püssiga, mille vedru on kokku surutud (negatiivsed laengud ligistikku surutud) ja siis triklisse kinni pandud (O-sillaga seotud). Tarvitseb vaid trikkel päästa (O-sild hüdrolüüsida), kui püssikuul (kolmas fosfaatrühm) lendab suure kiirusega eemale. Selle näite alusel on kerge mõista, et ATP energia aluseks on kokkusurutud tõukejõud, samal ajal kui redoks energia aluseks on lahkutõmmatud tõmbejõud. Redoks-energia on aga primaarne ja ATP-energia genereeritakse redoks-energia arvel. Seda ei tehta mitte otse, sest elektronid ei saa ATP sünteesi ensüümi käivitada, vaid vahepealse energiakandja, prootonite (vesinik-ioonide) abiga. Redoks-energia vabanedes transformeeritakse osa sellest prootonite energiaks, mille abiga lõpuks sünteesitakse ATP.
Prootonite energia seisneb selles, et nende kontsentratsioon ühel pool biomembraani on suurem kui teisel pool. Kuna biomembraan on lipiidne kasik-kiht, mis ei luba ioone läbi liikuda, siis on võimalik prootonite kontsentratsiooni suurendada ühel pool membraani ja vähendada seda teisel pool membraani. Vastavad valgukompleksid, mis töötavad prootonpumpadena kui neid läbib redoks-reaktsiooni elektronvoog, on tuntud nii kloroplastides kui mitokondrites. Tulemusena kogunevad prootonid ühele poole membraani tunduvalt suurema kontsentratsioonis kui teisele poole. Kloroplastides pumbatakse prootonid tülakoidi (membraanist kotikesetaolise moodustise) sisemusse, mitokondrites aga seest välja, tsütoplasmat ja mitokondrit eraldavate kahekordsete membraanide vahele.
Elektrivälja energia membraanilKui prootonid liiguvad läbi membraani, siis tekib membraanil otsekohe elektripotentsiaalide vahe, potentsiaal on positiivsem sealpool, kus prootoneid on rohkem. Mitokondri membraanil võib potentsiaalide vahe ulatuda kuni 0.15 V. Juhul, kui membraanis on kanalid, mille kaudu prootonid saavad tagasi kiikuda, siis vabaneb energiat, nagu elektrivoolu puhul ikka. Tuletame meelde elektri põhisuurused ja seosed.
Elektrilaengu ühikuks on Kulon (lühend C, prantsuse teadlase nimest Coulomb), mis võrdub ??? prootoni (või elektroni) laenguga.
Voolutugevus on suurus, mida mõõdetakse elektrijuhet ajaühikus läbinud laenguühikute arvuga. Voolutugevuse ühikuks on Amper (lühend A, prantsuse teadlase nimest Ampere). Voolutugevus on üks A, kui juhet läbib üks C s-1. Tegelikult kulon defineeritaksegi voolutugevuse kaudu. Kui kahte ühe meetri kaugusel asuvat paralleelset juhet läbib vool 1 A, siis mõjub nende vahel magnetjõud 1 N.
Elektrivälja kahe punkti potentsiaalide vahet (rahvakeeles “pinget”) mõõdetakse tööga, mida tuleb teha, et ühikulist laengut viia ühest välja punktist teise. Tööd tehakse siin elektrivälja jõu vastu.
Potentsiaalide vahe ühik on Volt (lühend V, itaalia teadlase nimest Volta). Elektrivälja kahe punkti potentsiaalide vahe on üks V, kui laengu 1 C viimisel ühest punktist teise tehakse tööd 1 J. Näiteks meie elektrivõrgus on kahe juhtme potentsiaalide vahe 220 V, galvaani elemendis on see 1.5V, auto seatina-akus 2V.
Nendest definitsioonidest on selge, et laengu üks C liikumisel läbi mitokondri membraani tehakse tööd 0.15 J, kui potentsiaalide vahe ühel ja teisel pool membraani (lühidalt ka ‘membraanpotentsiaal’) on 0.15 V.
Laengu ühik C tuletati elektrivoolu magnetjõu kaudu, sidudes selle mehaanikas defineeritud jõu ühikuga. Sellest tulenevalt osutus täiesti juhuslikult, et ühes Kulonis on ???? prootonit (või elektroni). Keemias aga kasutatakse molekulide hulga mõõtmiseks suurust mool, mis sisaldab Avogadro arvu (Na = 6.02 1023 ) molekuli. Neid arve võrreldes leiame, et üks mool prootoneid kannab laengut 96500 kulonit. Seega, kui üks mool prootoneid läbib elektrivälja potentsiaalide vahe 1 V, siis tehakse tööd 96500 J mol-1 = 96.5 kJ mol-1. Seda arvu nimetatakse Faraday arvuks (lühend F, inglise teadlase nimest). Membraanpotentsiaalide vahe puhul 0.15 V on vastav töö 14.5 kJ mol-1 . Niiviisi arvutamegi membraanpotentsiaali energiat (tööd) membraani läbivate prootonite mooli kohta:
![]()
kus Ee tähistab membraani energia elektrilist komponenti, on membraanpotentsiaal (V), F on Faraday arv ja n tähistab ionisatsiooniastet. Viimane tegur on juurde toodud selleks, et valem oleks õige ka ioonide jaoks, mis kannavad kahte või enamat laengut ja mille jaoks n= 2 või enam. Prootoni jaoks n = 1.
Mõnedes membraanides (näiteks tülakoidides kloroplastis) on ioone juhtivad kanalid, mis lasevad läbi Mg2+ ioone kuid ei lase läbi prootoneid. Prootonite transportimisel tekkiv membraanpotentsiaali vahe sunnib siis Mg ioone likuma vastassuunas läbi nende kanalite, iga kahe prootoni vastu üks Mg2+ ioon. Niiviisi tasakaalustatakse prootonite elektriväli samanimeliste ioonidega teisel pool membraani ja membraanil ei tekigi suurt potentsiaalide vahet (umbes 10 mV siiski jääb, mis tõukab Mg ioone). Niisugusel membraanil elektriväljast tingitud energia praktiliselt puudub, kuid seevastu prootonite kontsentratsioonide vahe võib kasvada väga suureks, sest puudub vastutöötav elektrijõud. Ka molekulide (ioonide) kontsentratsioonide vahe membraaniga lahutatud ruumiosades sisaldab energiat, sest difusiooni tõttu püüavad molekulid kõrgema kontsentratsiooniga ruumiosast madalama kontsentratsiooniga ruumiosasse liikuda.
Kontsentratsioonide erinevuse energia
Selleks, et koguda prootoneid ühele poole membraani tuleb ilmselt teha tööd. Vastupidi, kui kontsentratsioonide erinevus on olemas, siis see on võimeline tööd tegema. Tuletame valemi kontsentratsioonide erinevuse potentsiaalse energia arvutamiseks.
Kujutleme, nagu osmoosi puhulgi, et prootonid on gaas, mis on erineva tihedusega ühel ja teisel pool membraani. Võtame lihtsustuseks suure mudeli, kus kummalgi pool membraani on üks mool prootongaasi, kuid erineva tihedusega. Kontsentratsioonide (tiheduste) erinevuse potentsiaalne enrgia on niisama suur kui suur on töö, mida tuleb teha, et see erinevus kaotada, näiteks surudes hõredamat gaasi kokku (tehes välist tööd) või lastes tihedamat gaasi paisuda (lastes gaasil tööd teha). Gaasi kokkusurumise tööd saab aga arvutada kui rõhu ja ruumala muutuse korrutist. Kahjuks aga ei jää rõhk ruumala muutudes konstantseks vaid suureneb ruumala vähenedes. Seega tuleb rõhk avaldada ruumala funktsioonina gaaside võrrandist ja siis töö arvutada integraalina.
Elelentaartöö
![]()
Arvutame rõhu:
![]()
ja asendame töö valemisse
![]()
Töö, mille teeme surudes gaasi kokku ruumalalt V1 ruumalale V2 leiame integraalina
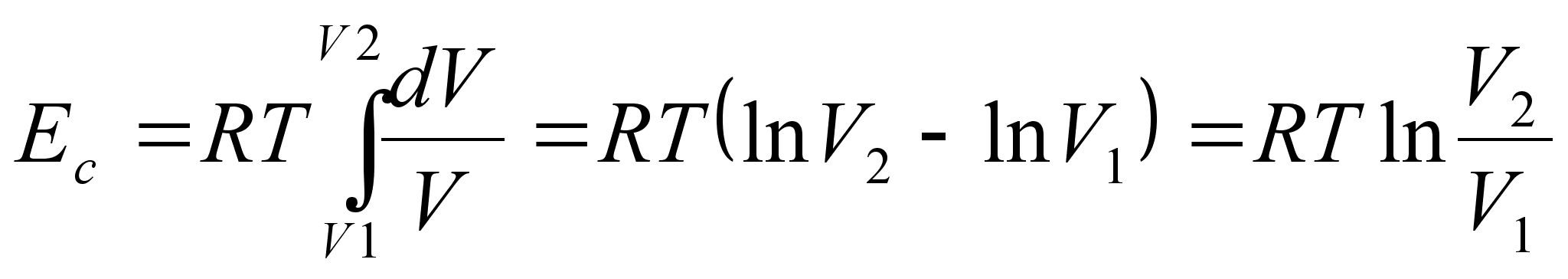
Arvestades, et
![]()
saame
![]()
kus C tähistab juba lahustunud aine (prootonite) kontsentratsioone.
Seega on kontsentratsioonide erinevusest tingitud töö ühe mooli kohta määratud kontsentratsioonide suhtega, mitte nende vahega. Kui membraanil on nii kontsentratsioonide erinevus kui ka potentsiaalide erinevus, on summarne energia
![]()
Füüsika: sissejuhatus.
Füüsika on teadus kehade vastasmõjudest ja nendest põhjustatud liikumistest. Kehade vastasmõju avaldub jõuväljana.
“Keha” tunneme sellest, et tal on olemas mass, mis väljendub likumise inertsi ja gravitatsioonina. Kehal võib olla ka elektrilaeng, mis väljendub vastasmõjus teise laetud kehaga elektrivälja kaudu. Kõige elementaarsemad kehad on näiteks elektron ja prooton, mis moodustavad aatomid. Aatomitest moodustuvad molekulid. Suuremad kehad koosnevad omavahel seotud paljudest aatomitest või molekulidest. Paljuaatomilised kehad võivad olla tahked, vedelad või gaasilised, sõltuvalt jõudude tugevusest, mis aatomeid (molekule) seovad. Kehad mõjutavad üksteis kaugelt, jõuväljade kaudu.
Keha “jõuväli” on kõikjal tema ümber ruumis, kuni lõpmatu kaugele. Jõuväljas asuvale teisele kehale mõjub jõud, aga samuti mõjub jõud teise keha jõuväljas asuvale esimesele kehale. Nii mõjutavadki kehad üksteist kaugelt jõuväljade kaudu. Kaugmõju väljade kaudu on ainus kehade vastastikune mõju looduses. Gravitatsiooniline kaugmõju on silmaga nähtav universumi ehituses, elektromagnetiline kaugmõju aga domineerib aatomite ja molekulide vahel, sealhulgas ka siis, kui kehad “silmnähtavalt” kokku puutuvad. Niisugust nähtust nagu “kokkupuutumine” ei ole olemas. Kehad ei puutu kunagi tegelikult kokku, maksimaalses läheduses aatomite välised elektronkihid satuvad lähestikku ja negatiivsed laengud tõukuvad üksteise jõuväljas, takistades kehade edasist lähenemist. Kui jätame kõrvale tuumasisesed jõud, siis need kaks, gravitatsiooniline ja elektromagnetiline, ongi ainsamad jõud, mis määravad aatomite ja molekulide paigutuse kehades ja kehade paigutuse kosmilises ruumis, seega kogu looduse ehituse.
Käesolevas kursuses püüamegi muuta loodust mõistetavamaks tema atomaarse-molekulaarse struktuuri kaudu. Kogu looduse struktuur alates aatomitest ja lõpetades universumiga, kaasa arvatud eluslooduse struktuur, saab mõistetavaks kui tunneme füüsikaseadusi, mis määravad kehade võimaliku asendi üksteise jõuväljades. Suhteliselt väike arv põhilisi füüsikaseadusi määrab elektronide paigutuse aatomis, aatomite paigutuse molekulis, molekulide paigutuse kehas. Selge, et elementaarkehade arvu suurenedes nende vastastikune mõju muutub väga keeruliseks ja seda analüüsida ei ole lihtne. Füüsika on võimeline detailselt kirjeldama vaid suhteliselt lihtsaid struktuure, keerukamate puhul tuleb rakendada loogilise ekstrapolatsiooni meetodit, püüdes ette kujutada, kuidas lihtsaid struktuure valitsevad seadused kombineeruvad keerukamates struktuurides. See ongi mõttetegevus, mõtlemine, mida ootan bioloogidelt kui nad asuvad rakendama käesolevas kursuses omandatut oma erialal.
Füüsikat peetakse tavaliselt matemaatiliseks teaduseks, mis tihtipeale põhjustab hirmu. See ei ole aga nii. Matemaatiline on vaid üks teadus – matemaatika. Loodusteadusi, kaasa-arvatud füüsikat, on võimalik, isegi ainuvõimalik, mõista ilma matemaatikat rakendamata. Matemaatiline valemite keel on rakendatav lihtsate seoste lühidaks kirjeldamiseks. Näiteks teades, et auto läheneb kiirusega 50 km/h ja asub praegu minust 50 m kaugusel saan ma arvutada, et ta jõuab minuni t=s/v=50/(50x1000/3600)=3.6 sekundi pärast. Teades, et ma kõnnin kiirusega 5 km/h kulub mul 10 m laiuse tänava ületamiseks 10/(5x1000/3600)=7.2 s. Ilmselt ei ole otstarbekas tänavaületamist alustada, sest jään auto alla just tee keskpaigas. Kas ma aga tänaval seistes teen need arvutused? Kindlasti mitte, vaid ma kujtlen, kuidas auto jätkab oma liikumist, kuidas mina astuks üle tee ja ma näen “vaimusilmaga”, kuidas auto sõidaks mulle peale. Niisugune kujutlemine on välismaailma modelleerimine mõttes, see ongi mõtlemine. Füüsika täilelikuks mõistmiseks ei tohi mitte valemeid ega konspektilehtedel asetsevaid lauseid endale vaimusilma ette manada, vaid protsesse, kehasid ja nende liikumisi. Ei ole suur häda, kui te aatomit või molekuli kujutlete teistsugusena kui ta tegelikult on, suurem on häda kui te teda üldse ette ei kujuta. Selge, et suure hulga aatomite-molekulide liikumise ette kujutamine võib olla raske, aga veel raskem oleks nende matemaatiline kirjeldamine. Näiteks kvantmehaaniliselt on lahendatud vaid kahe keha vastasmõju probleem. Kolme või rohkema keha puhul tuleb juba kasutada mitmesuguseid lähendusvõtteid, milles matemaatika ja loogiline ettekujutus põimuvad. Niisiis, asjade mõistmiseks tuleb just neidsamu asju modelleerida, ette kujutada, mitte aga meelde tuletada valemeid või lauseid, mis nende kohta käivad. Siit tulebki vahe mõistete “tean” ja “mõistan” vahel. “Teatakse” fakte. Tüüpiline näide on siin mälumängurite kiired vastused Jeopardy turniiril. Mnemoturniiril aga antakse aega, ja ilus on pealtkuulata, kuidas loogilise arutelu, mõtlemise teel jõutakse õige vastuseni ka siis, kui seda keegi osavõtjatest alguses ei tea. Vastus, mida ei teata, mõeldakse välja. Õige vastuse väljamõtlemine igal elujuhtumil ongi asjade mõistmise tunnus. Füüsikas on heaks mõistmise kontrolliks ülesannete lahendamine. Ilma ülesandeid lahendamata ei ole te seda füüsikakursust kindlasti mitte mõistnud. Mõistmise ja teadmise dialektika on tihedalt seotud teoreetilise ja eksperimentaalse teaduse dialektikaga.
Eksperiment ja teooria teaduses.
Me saame oma teadmised loodusest vaatluste ja eksperimentide tulemustena. Vaatlused, näiteks astronoomilised või ökoloogilised, on looduses iseenesest toimuvate protsesside passivne registreerimine, jälgimine. Eksperiment (katse) on aktiivne vahelesegamine looduslikesse protsessidesse tahtlikult muutes nende toimumise tingimusi. Eksperiment ja vaatlus annab meile teadmise, mis toimub teatud objektidega teatud tingimustes. Näiteks saame teada, et teatud täht kiirgab mingi intensiivsusega ja mingi spektraaljaotusega valgust, või et bakterirakk kasvab mingi kiirusega. Need on faktid, mis iseloomustavad ainult ja ainult seda konkreetset situatsiooni milles katse või vaatlus tehti. Kui aga on tarvis teada, millal see täht (näit. meie Päike) plahvatab supernoovana või kui sageli bakterirakk pooldub, siis nendest katsetest vastust ei saa. Kuigi bakterite paljunemise kohta saaks ju teha vastava katse, siis Päikese plahvatuse puhul oleks seda hilja vaadelda. Kui me oleme tõepoolest mõistnud tähe evolutsiooni ja raku elutsüklit, siis peaksime olema võimelised teoreetiliselt ette ennustama nii pooldumist kui plahvatust. Ennustada saab teooria baasil, ekstrapoleerides seda kas ainult loogilise mudeli või siis ka matemaatilise mudeli abil. Teooria ongi tegelikult loodusliku protsessi peegeldus, selle mudel meie mõtlemises. Teooria on tunnetuse, mõistmise täiuslikem etapp. Kuidas aga tekib teooria meie käsutuses olevate vaatlustulemuste kaudu?
Vaatlused ja eksperimendid esitavad tulemustena teatud fakte, mis on tõesed olukordade tarvis, milles need saadi. Peaks tegema lõpmatu palju eksperimente, et saada vastused mõeldavate olukordade kohta, ja ikka jääks veel lõpmatu palju olukordi, mille kohta eksperimenti tehtud ei ole. Ülaltoodud näites autoga tähendaks niisugune empiiriline lähenemine seda, et auto asukoht tuleks mõõta igal ajahetkel, sest ilma teooriata kuidagi ei saa ju teada, kus ta saab asuma järgmise sekundi, kümnendiku, sajandiku jne pärast. Kui meil on aga teooria, et auto liigub ühtlaselt ja sirgjooneliselt kiirusega 50 km/h, siis saame kindlusega ette ennustada, kus ta saab asuma näiteks 3.6 sekundi pärast. Kuidas tekkis aga ühtlase ja sirgjoonelise liikumise teoreetiline ettekujutus, kas selleks tehti lõpmatu palju mõõtmisi ja siis üldistati? Ei, oli vaja mõõta keha asukoht ja aeg ainult kolmes punktis ja avastada seaduspärasus, et võrdsete teepikkuste läbimiseks kulus võrdne aeg. Seda seaduspärasust aga mõõtmistulemused meile ette ei ütle, see tuleb endal avastada tulemusi analüüsides. Siin avaldubki eksperimentaalse ja teoreetilise teadusliku tunnetuse dialektika: ühelt poolt baseerub teooria eksperimentide tulemustel, teiselt poolt ei ole olemas reeglit ega seadustpära, mille järgi eksperimentide tulemuste põhjal luua teooria. Teooria on niisugune loogiline (matemaatiline) protsessi mudel, mis rahuldab kõiki olemasolevaid eksperimenditulemusi. Teooriat võib luua ka siis, kui on olemas kas või üksainus eksperiment, aga tavaliselt ei ole see teooria siis võimeline rahuldama teise eksperimendi tulemust (ei lange sellega kokku). Mida rohkem on eksperimente, mida antud teooria rahuldab, seda tõenäosem on, et ta rahuldab ka uusi, veel tegemata eksperimente, seega, on võimeline tulemusi õigesti ette ennustama. Teooria, mis rahuldab paljude eksperimentide tulemusi, ei tulene aga üldse nendest eksperimentidest, vaid on omaette sõltumatu loogiline mudel, mis sünnib mõttetöö tulemusena. Tavaliselt arvatakse, et teadlastel on mingi eriline intuitsioon, mis aitab neil leida õiget teooriat. Näiteks, kuidas küll Mendelejev taipas, et elemendid grupeeruvad perioodiliselt kaheksa kaupa? Kuidas küll Einstein tuli mõttele, et kahe liikuva keha kiiruste liitumisel summaarne kiirus ei saa ületada valguse kiirust? Darwin nägi ainult liikide lõputut mitmekesisust, kuid kuidas ta seletas seda loodusliku valiku tulemusena? Tegelikult ei ole mingit erilist intuitsiooni, vaid lõputu pingeline mõttetöö. Tuleb läbi mõelda ja loogiliselt käivitada palju erinevaid mudeleid, millest suurem osa ei rahulda mõnda eksperimenti ja tuleb seega kõrvale heita, kuni leitakse üks või isegi mitu mudelit, mis rahuldavad kõiki teadaolevaid eksperimente. Muide, mõne teooria loomise puhul on juhtunud, et üks või paar eksperimenti kangekaelselt ei sobi sellesse, sel ajal kui ülejäänud kõik sobivad. Siis võib tõsta ka küsimuse nende eksperimentide korrektsuse kohta. Siit tuleneb veel üks tagasiside eksperimendi ja teooria vahel: eksperiment ei ole mitte ainult alus teooria kontrolliks, vaid teooria võib kontrollida ka eksperimendi korrektsust. Muidugi, nii nagu malemängugi puhul, head mängijad ei vaagi kaugeltki kõiki võimalikke käike vaid valivad kiiresti kõige perspektiivikamad, sellega kompuutermaletajast erinedes, niisamuti head teadlased ei vaagi kaugeltki mitte kõiki võimalikke teooria variante vaid valivad kiiresti perspektiivikamad. Selles ehk väljendubki “intuitsioon”, mis tegelikult on kogemus ja eelteadmised.
Matemaatiline ja loogiline teooria
Teooria on maailmapilt, mis käivitub meie mõtlemises. Mõtlemise tugev külg on suhteliselt keerukate süsteemide kiire kvalitatiivne analüüs. Kui hinnata tuleb aga kvantitatiivseid suurusi, siis jääb mõtlemine üsna varsti jänni ja kutsub appi matemaatika. Matemaatilised valemid ei ole midagi muud kui lühidalt kirjapandud reeglid numbriliste suurustega opereerimiseks, seega kvantitatiivseks mudeli (teooria) analüüsiks. Ühe ja sellesama valemiga võib kirjeldada väga erinevaid protsesse, mis on oma käitumiselt sarnased, kuigi sisult täiesti erinevad. Seega on vajalike matemaatiliste valemite arv tunduvalt väiksem kui analüüsitavate protsesside arv. Vaatleme järgnevas peamisi matemaatiliste avaldiste tüüpe, mis kursuses käsitletavate füüsikaliste protsesside analüüsil ette võivad tulla.
Funktsioonid
Funktsioon
on matemaatiline seos mitme suuruse vahel, mille järgi saab
arvutada tundmatu suuruse (nimetatakse ka funktsiooniks, y)
väärtuse kui argumentide xi väärtused
on teada:![]() ,
kus f tähistab mingit matemaatilist arvutusreeglit
(tehteid ja nende kombinatsioone). Lihtsaim on ühe muutuja
funktsioon
,
kus f tähistab mingit matemaatilist arvutusreeglit
(tehteid ja nende kombinatsioone). Lihtsaim on ühe muutuja
funktsioon ![]() .
Levinuim astmefunktsioon on lineaarne (sirge) ehk esimese astme
sõltuvus:
.
Levinuim astmefunktsioon on lineaarne (sirge) ehk esimese astme
sõltuvus:![]() ,
kus a on mingi algseis millest protsess algab ja b
tähistab y kasvu suhtelist kiirust võrreldes x
kasvuga, näit. läbikäidud tee sõltuvus ajast,
voolutugevuse sõltuvus pingest, veevoolu sõltuvus
rõhkude vahest, difusioonivoo kiiruse sõltuvus
kontsentratsioonide vahest; lineaarfunktsiooni erijuht on
proportsionaalne sõltuvus, kus a = 0 ja mõlemad,
nii x kui y alustavad muutumist nullist. Teise astme
funktsioon on ruutsõltuvus, mis võib sisaldada osana ka
lineaarsõltuvust, kuid lihtsuse mõttes jätame
selle praegu välja:
,
kus a on mingi algseis millest protsess algab ja b
tähistab y kasvu suhtelist kiirust võrreldes x
kasvuga, näit. läbikäidud tee sõltuvus ajast,
voolutugevuse sõltuvus pingest, veevoolu sõltuvus
rõhkude vahest, difusioonivoo kiiruse sõltuvus
kontsentratsioonide vahest; lineaarfunktsiooni erijuht on
proportsionaalne sõltuvus, kus a = 0 ja mõlemad,
nii x kui y alustavad muutumist nullist. Teise astme
funktsioon on ruutsõltuvus, mis võib sisaldada osana ka
lineaarsõltuvust, kuid lihtsuse mõttes jätame
selle praegu välja:![]() näit. pindala sõltuvus lineaarmõõdust
(ringil raadiusest või ruudul küljest), kineetilise
energia sõltuvus kiirusest. Kolmanda astme funktsioon ehk
kuupsõltuvus
näit. pindala sõltuvus lineaarmõõdust
(ringil raadiusest või ruudul küljest), kineetilise
energia sõltuvus kiirusest. Kolmanda astme funktsioon ehk
kuupsõltuvus![]() ,
näit. ruumala sõltuvus lineaarmõõdust, nagu
kera ruumala sõltuvus raadiusest, kuubi ruumala sõltuvus
külje pikkusest. Ka pöördvõrdeline sõltuvus
on astmefunktsioon:
,
näit. ruumala sõltuvus lineaarmõõdust, nagu
kera ruumala sõltuvus raadiusest, kuubi ruumala sõltuvus
külje pikkusest. Ka pöördvõrdeline sõltuvus
on astmefunktsioon: ![]() ,
näit. voolukiiruse sõltuvus takistusest, liikumiseks
kulutatud aja sõltuvus teepikkusest. Pöördvõrdelise
ruutsõltuvuse näiteks on
,
näit. voolukiiruse sõltuvus takistusest, liikumiseks
kulutatud aja sõltuvus teepikkusest. Pöördvõrdelise
ruutsõltuvuse näiteks on ![]() ,
näit. punktikujulise laengu või massi elektri- või
gravitatsioonivälja tugevuse sõltuvus kaugusest
keskpunktist. Oluline funktsioon on eksponentsiaalne sõltuvus.
Positiivne eksponent
,
näit. punktikujulise laengu või massi elektri- või
gravitatsioonivälja tugevuse sõltuvus kaugusest
keskpunktist. Oluline funktsioon on eksponentsiaalne sõltuvus.
Positiivne eksponent ![]() kirjeldab
näit. bakterikoloonia kasvu ajas, kapitali suurenemist firmas.
Negatiivne eksponent
kirjeldab
näit. bakterikoloonia kasvu ajas, kapitali suurenemist firmas.
Negatiivne eksponent ![]() kirjeldab
näit. radioaktiivselt lagunevate tuumade arvu, valguskvantide
arvu vähenemist neelavat keskkonda läbides, kondensaatori
laeng tühjenemist läbi takisti, edukate üliõpilaste
arvu kahanemist õppeaja jooksul.
kirjeldab
näit. radioaktiivselt lagunevate tuumade arvu, valguskvantide
arvu vähenemist neelavat keskkonda läbides, kondensaatori
laeng tühjenemist läbi takisti, edukate üliõpilaste
arvu kahanemist õppeaja jooksul.
Joonistada graafikud.
Diferentsiaalvõrrandid
Diferentsiaalvõrrandid
on matemaatilised seosed mitte suuruste eneste, vaid nende muutuste
vahel. Näiteks võiks olla ühtlaselt kiireneval
liikumisel läbitud teepikkus. Liikumisel kiirusega v on
igas lõpmatu lühikeses ajavahemikus dt läbitud
teepikkus ![]() .
Kui kiirus v on konstant, siis niisugune võrrand laheneb
lihtsalt:
.
Kui kiirus v on konstant, siis niisugune võrrand laheneb
lihtsalt: 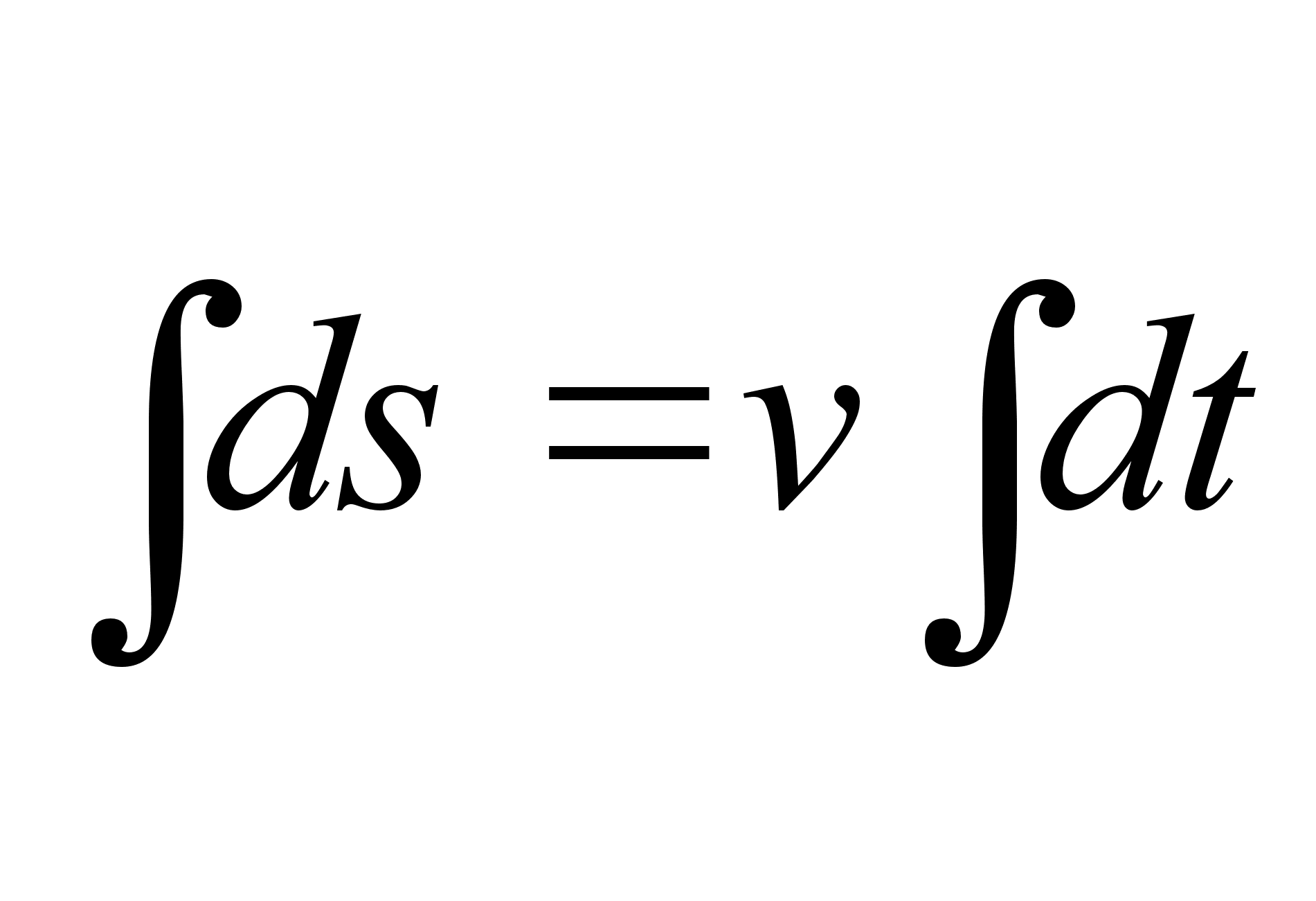 ehk
ehk ![]() ,
kus s0 tähistab liikumise alguspunkti. Esimest
järku diferentsiaalvõrrand annab lahendina
funktsiooni (s) muutuse, kuid ei ole teada, millisest
algpunktist muutumist alustati. Integreerimiskonstant s0
näitabki, et sealt alustati liikumist ja s on siis
lõpp-punkti tegelik asukoht. Veidi keerukam on juht kui
integreeritav suurus, antud juhul kiirus v, ei ole konstantne,
vaid muutub koos ajaga, näiteks kui on tegemist ühtlaselt
kiirineva liikumisega
,
kus s0 tähistab liikumise alguspunkti. Esimest
järku diferentsiaalvõrrand annab lahendina
funktsiooni (s) muutuse, kuid ei ole teada, millisest
algpunktist muutumist alustati. Integreerimiskonstant s0
näitabki, et sealt alustati liikumist ja s on siis
lõpp-punkti tegelik asukoht. Veidi keerukam on juht kui
integreeritav suurus, antud juhul kiirus v, ei ole konstantne,
vaid muutub koos ajaga, näiteks kui on tegemist ühtlaselt
kiirineva liikumisega ![]() .
Sel juhul
.
Sel juhul 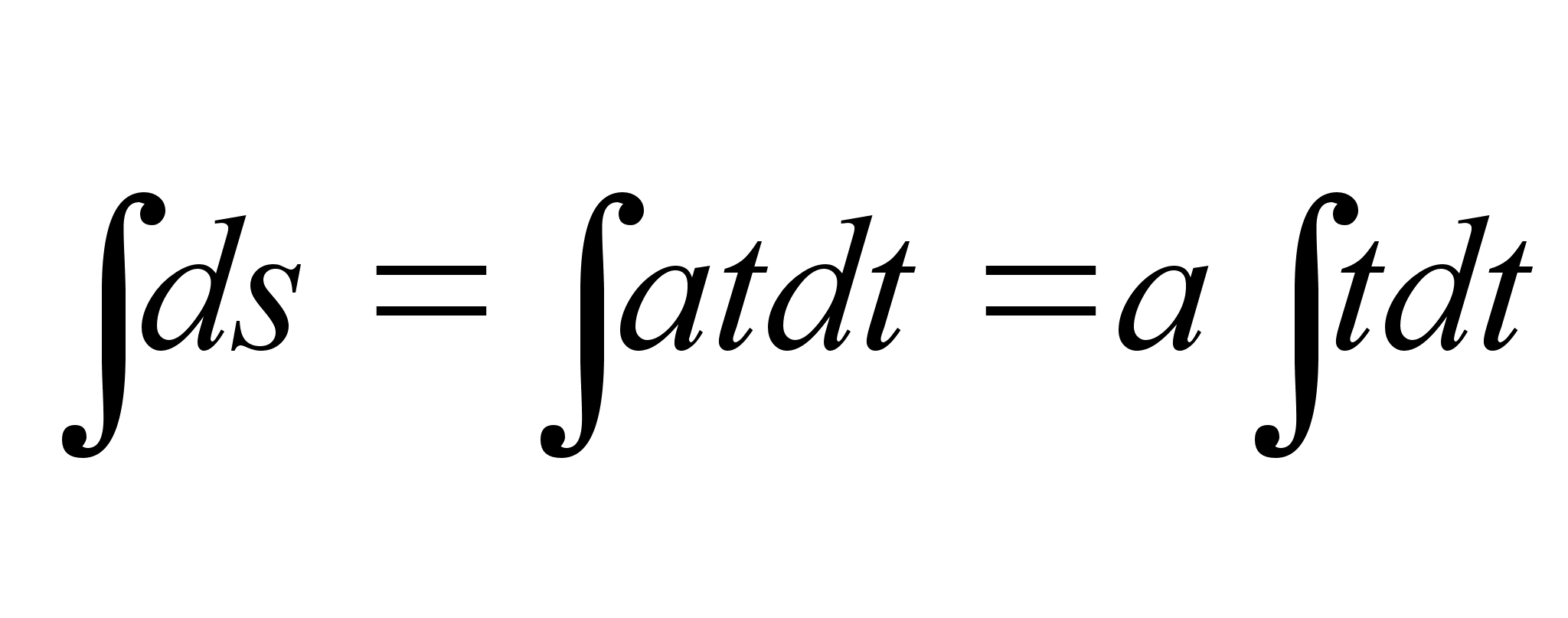 ja integreerides saame
ja integreerides saame ![]() .
Astmefunktsiooni integreerimise reeglid toome allpool.
.
Astmefunktsiooni integreerimise reeglid toome allpool.
Väga tihti on tegu järgmise diferentsiaalvõrrandiga, mis baseerub teadmisel, et suuruse A muutumise kiirus (ajas) on võrdeline suuruse A enesega. Nii on see näit. vedeliku väljavoolamisel reservuaarist, elektimahtuvuse tühjenemisel, radioaktiivse aine lagunemisel, valguskvantide liikumisel läbi neelava aine, kus
![]() ;
;
Siit edasi
![]() ja
ja
![]() ning integreerides saame
ning integreerides saame ![]() ja
ja ![]() ,
,
millest
![]()
Nagu panite tähele, integreerimiskonstant kirjutati seekord logaritmi kujul, lnA0 , et muutuse alguspunkt viia sisse suhtena, mitte vahena lõpp-punkti suhtes. Viimase valemi võib kirjutada ka kujul
![]() .
.
kus =1/k. Need valemid kujutavad eksponentsiaalseid protsesse ja on nn. eksponendi tegur (antud juhul ajategur), k aga on kiiruskonstant. Aja möödudes on eksponentsiaalselt kahanev protsess vähenenud suhtes e-1=0.368. Kahe ajateguri möödudes e-2 = 0.135 ja e-3=0.050. Seega, eksponentsiaalsete protsesside praktilise lõppemiseni kulub vähemalt 3 kuni 5.
Kui diferentsiaalvõrrand näitab, et suurus mitte ei kahane, vaid kasvab iseendaga võrdeliselt, saame samasuguse eksponentsiaalse lahendi, aga positiivse astendajaga. Nii kirjeldub näiteks populatsiooni (bakterite koloonia) kasv, taime kasv, majanduse (kapitali) kasv etc. Aja t asemel võib esineda ka teepikkus, näiteks kui valguskvandid läbivad neelavat ainet või juhuslikult asetatud neelavaid objekte (taimkatte lehestik). Siis konstant k näitab valguse (või radioaktiivse kiirguse) nõrgenemist teepikkuse ühiku kohta.
Joonistada eksponentsiaalsete muutuste graafikud.
Kui esimest järku diferentsiaalvõrrand sidus omavahel argumendi ja funktsiooni muutumise kiirusi (esimest järku tuletisi), siis teist järku diferentsiaalvõrrand seob omavahel argumendi ja funktsiooni muutumise muutumise kiirusi (teist järku tuletisi). Teist järku diferentsiaalvõrrandi näiteks on võnkumiste võrrand, mis baseerub teadmisel, et pendlit (või vedru) tagasitõmbav jõud on võrdeline hälbega tasakaaluseisust A. Kuna jõud põhjustab kiirenduse, ehk kiiruse muutumise, siis väidab see võrrand, et võnkuva massi kiiruse muutumise kiirus (kiirendus) on võrdeline hälbega tasakaaluseisust ja suunatud tasakaaluseisu poole:
![]()
Selle võrrandi lahend on siinusfunktsioon, näiteks pendli võnkumine või murdja-ohvri populatsiooni võnkuv olek (Volterra võrrand). Lahendist nähtub, et periood väljendub järgmiselt:
![]() ehk
ehk 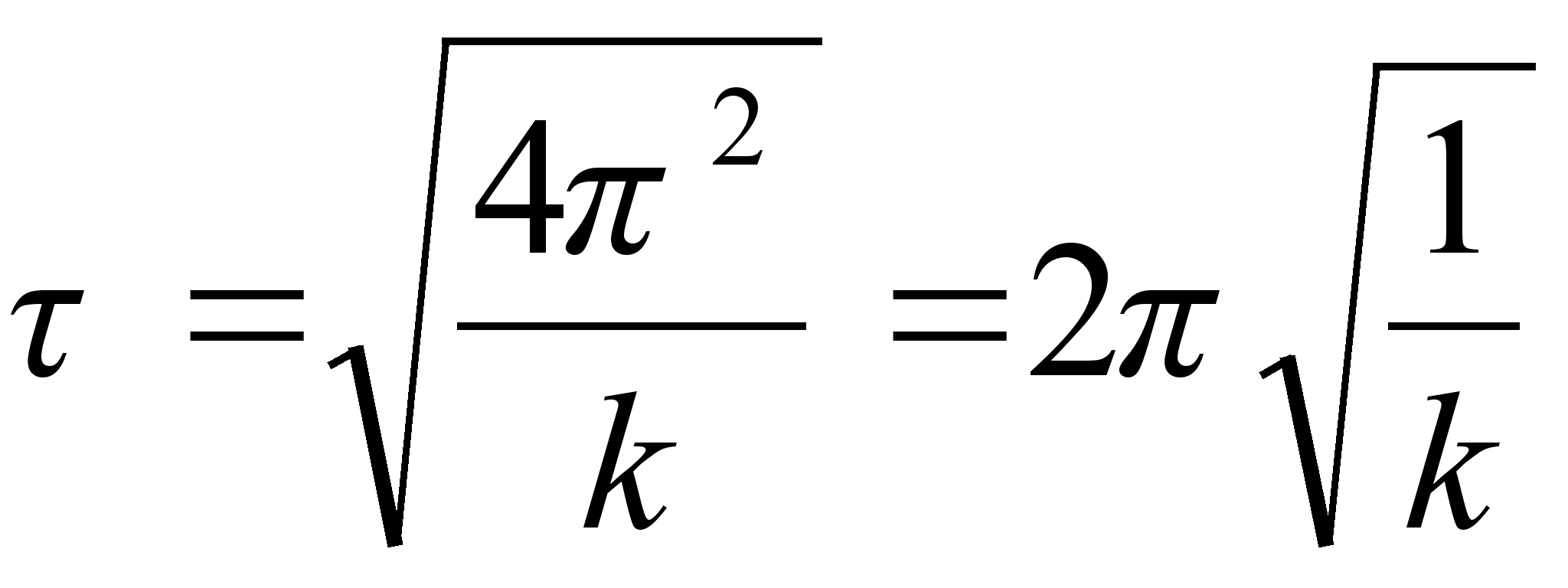
Selleks, et määrata, missuguses siinuse punktis asub lahend teatud ajahetkel, on lisaks võrrandi lahendiks olevale siinusfunktsioonile tarvis teada juba kahte algtingimust: algkoordinaati, millest liikumine algab ja liikumise algsuunda, kas tasakaalupunkti poole või sellest eemale.
INTEGRAALID
Ülaltoodud
diferentsiaalvõrrandite lahendamiseks pidime integreerima
funktsiooni, mis määras seose diferentsiaalide (väikeste
muutuste) vahel. Näiteks kui keha alustab liikumist
nullkiirusest ja liigub ühtlaselt kiirenevalt kiirendusega a
m s-2 , siis aja möödudes tema kiirus on v(t)
=at (tähistus v(t) tähendab, et
suurus v on aja t funktsioon). Selleks, et leida aga,
kui kaugele keha jõudis sellesama aja t jooksul, ei saa
lihtsalt lõppkiirust ajaga korrutada, vaid tuleb arvestada, et
igal ajahetkel oli keha kiirus erinev. Võib eeldada, et iga
väga lühikese ajavahemiku dt jooksul läbitud
teepikkus ![]() .
Keha asukoha muutuse leidmiseks pika ajavahemiku t2-t1
jooksul tuleb kasutada integraali:
.
Keha asukoha muutuse leidmiseks pika ajavahemiku t2-t1
jooksul tuleb kasutada integraali: 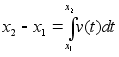 ehk antud juhul
ehk antud juhul
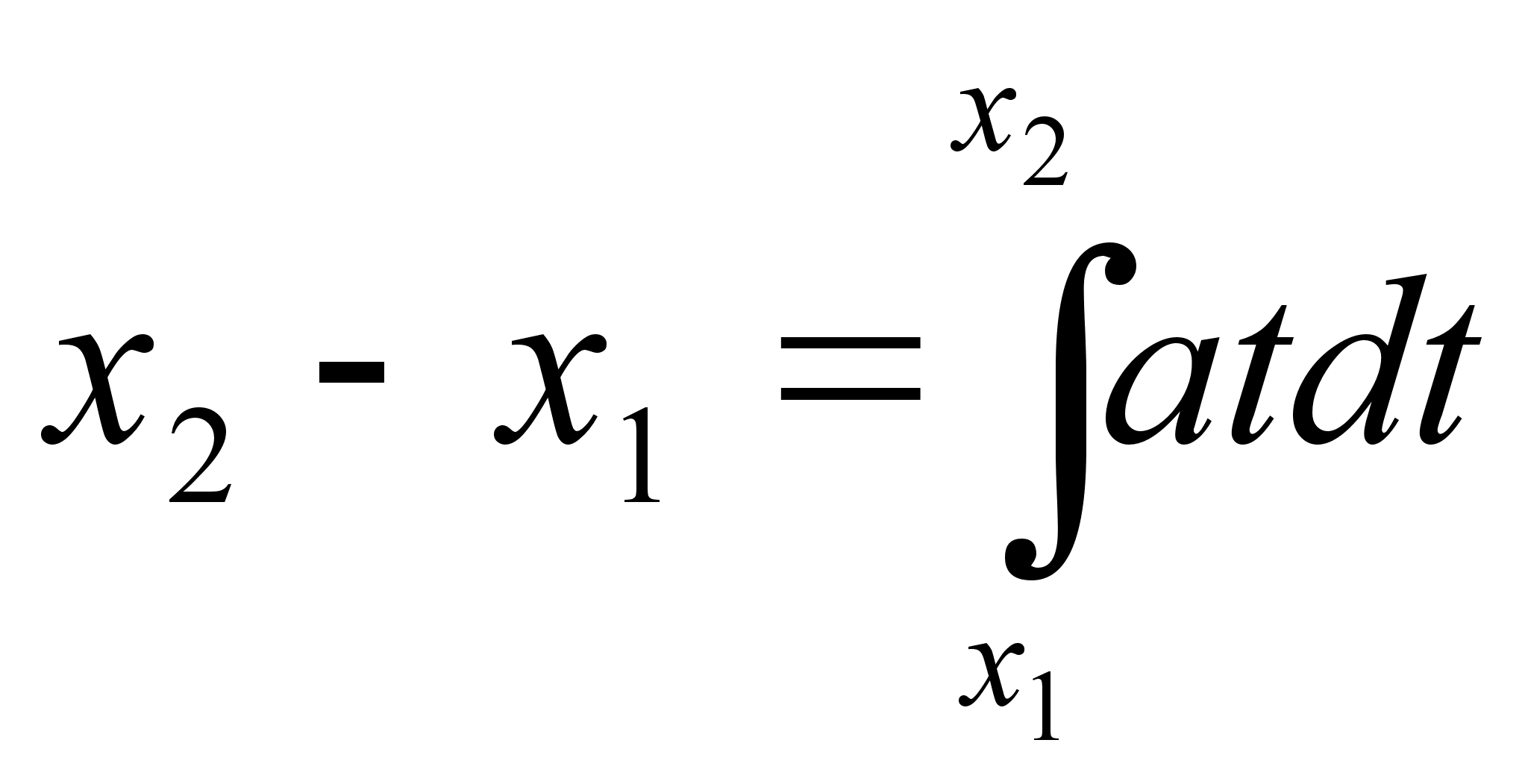
Integraali on lihtne leida kui v(t) on astmefunktsioon (antud juhul esimese astme funktsioon). Reegel on järgmine:
![]() ,
näiteks kui v=at siis
,
näiteks kui v=at siis 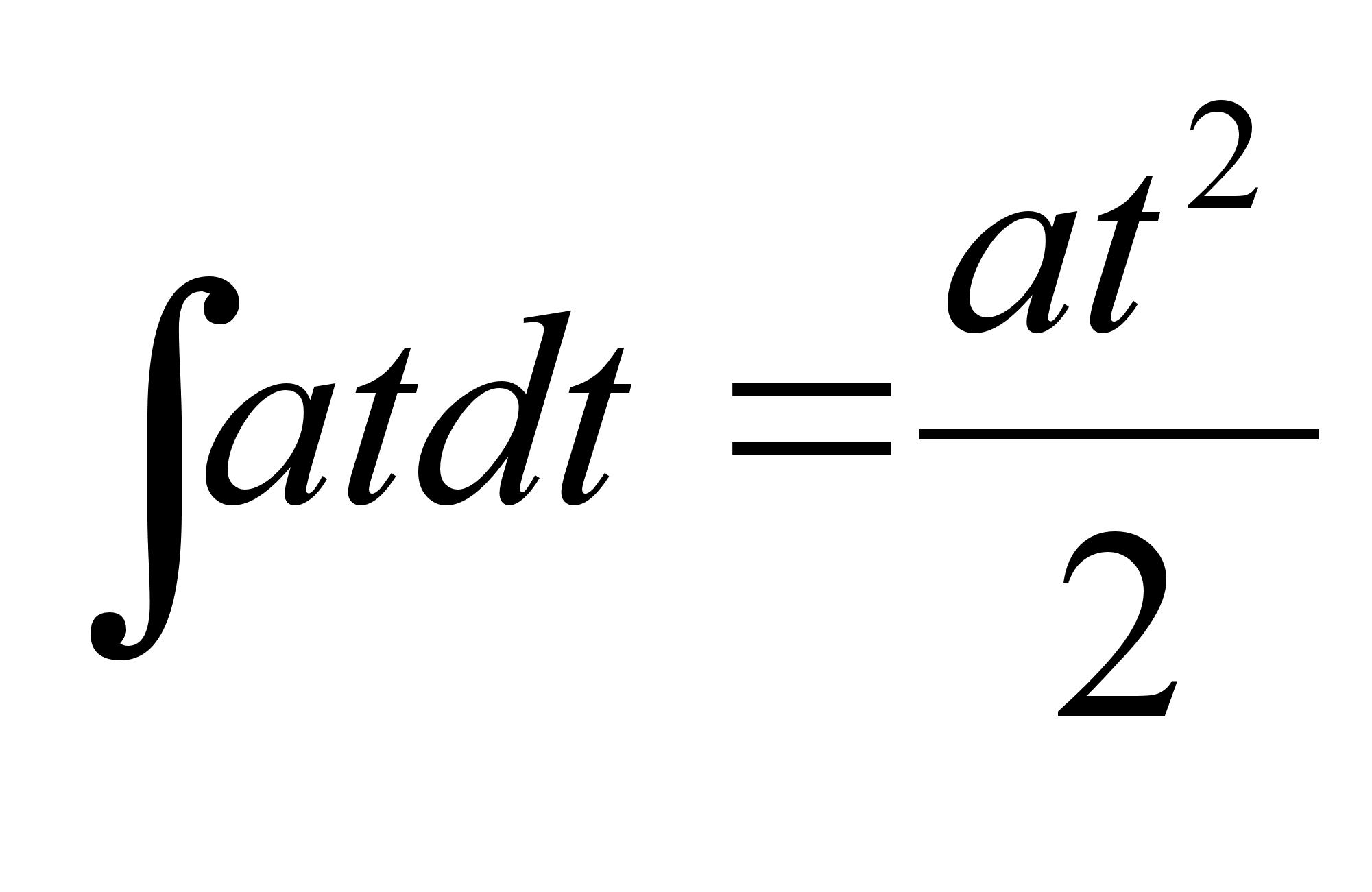 .
Veel näiteid:
.
Veel näiteid: ![]() ;
; ![]() ;
;
Aga peame
meeles et ![]() ja
ja
![]()
Ülaltoodud reeglid võimaldavad leida integraali funktsionaalse kuju, kuid selle tegeliku väärtuse arvutamiseks tuleb teada, missugusest integreeritava funktsiooni väärtusest summeerimist alustati ja missuguse väärtuse juures lõpetati. Pöördume kiireneva liikumise näite juurde tagasi ja küsime, kui pika tee läbis keha alates ajahetkest t1 ja lõpetaes ajahetkega t2? Seda arvutatakse nii, et leitakse määramatu integraali väärtus ülemisel rajal t2 ja lahutatakse sellest määramatu integraali väärtus alumisel rajal t1:
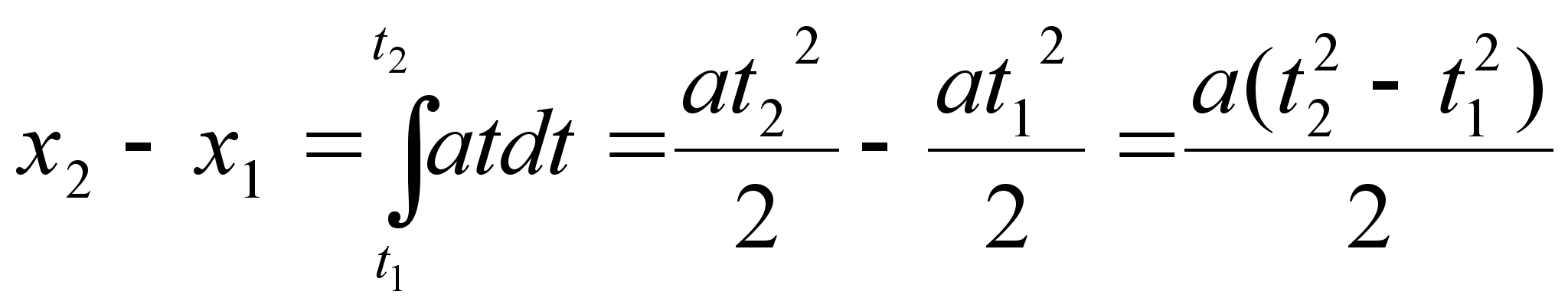
Kui t1=0 siis ![]() iga aja t jaoks, sest x1=0.
iga aja t jaoks, sest x1=0.
Kursuse jooksul kasutame integreerimist lisaks ebaühtlase kiirusega liikumisel läbitava teepikkuse arvutamisele veel näiteks aatomituuma ümbritseva elektrivälja potentsiaalse energia arvutamiseks ja gaasi paisumisel tehtava töö arvutamiseks.
Kinemaatika põhimõisted
Nagu öeldud, füüsika on teadus mis käsitleb kehade liikumist. Selleks aga tuleb defineerida liikumist kirjeldavad suurused ehk parameetrid, mis on: asukoht (koordinaadid), kiirus, kiirendus.
Asukoht (koodinaadid).
Keha asendi ja selle muutuste (liikumise) kvantitatiivseks kirjeldamiseks kasutatakse ruumikoordinaate. Koordinaadid on arvud, mis määravad keha kauguse mingitest kindlaksmääratud kohtaest, koordinaat-telgedest. Kolmemõõtmelises ruumis on asendi mäaramiseks vajalik kolm arvu (koordinaati), kahemõõtmelises (tasapinnal) kaks ja ühemõõtmelises (joonel) uksainus arv. Analoogiat edasi arendades saab ette kujutada ka enama kui kolemõõtmelisi ruume, näiteks võttes neljanda mõõtmena kasutusele aja, aga kui tarvis, veel teisi muutuvaid parameetreid. Sejuures on tähtis, et juurdetoodavad muutujad ei oleks seoste kaudu tuletatavad olemasolevatest, vaid oleksid täiesti sõltumatud, ortogonaalsed (piltlikult oleksid kõik teljed üksteisega risti, kuigi neid võib olle palju rohkem kui kolm).
Kõige sagedamini kasutatav koordinaat-teljestik on sirgete ristiolevate telgedega nn. ristkoordid e. Cartesiuse koordinaadid. Selles teljestikus määratakse keha asukoht kolme kauguse kaudu: esiteks liikudes piki x-telge, siis ristisuunas piki y-telge ja lõpuks ristisuunas piki z-telge. Kaugused x, y ja z kokkuleppelisest nullpunktist ongi keha riskoordinaadid. Riskoordinaadistikku kasutatakse näiteks USA-s linnade planeerimisel, kus ‘streedid’ ja ‘avenue’d on üksteisega risti ja nummerdatud kasvavas järjekorras alates linna keskpunktist. Positiivsete ja negatiivsete väärtuste asemel kasutatakse ‘North’, ‘South’, East’ ja ‘West’ lisandeid.
Cartesiuse koordinaadid ei ole ainuke viis keha asukoha määramiseks, vaid seda saab teha ka mõne testsuguse kolme arvu kombinatsiooni abil, peaasi, et kolm liikumist, mida need arvud kirjeldavad, oleksid ikka omavahel ristsuundades. Näiteks tsentraalsümmeetriliste (kerakujuliste ja kerakuju moondumisena tulenenud liikumiste) kirjeldamiseks on mugavamad nn. polaarkoordinaadid. Polaarkoordinaate on ka kolm, kuid ainult üks neist (raadius r) omab pikkuse (kauguse) dimensiooni, kaks ülejäänut on nurgad, mis määravad selle liikumise suuna, mida mööda minnes määratud punkti jõutakse. Esimene on nurk (teeta), mis määrab erinevuse vertikaalsihist ja teine on nurk , mis mäarab erinevuse kokkuleppelisest horisontaalsihist. Polaarkoordinaate kasutatakse geograafias, kus ‘põhjalaius’ on sisuliselt 90°- ja idapikkus on Kuna määratavad punktid asuvad kõik Maa pinnal, siis raadius oleks kõigi jaoks umbes 6000 km ja see jäetakse kirjutamata. Maapinna kohal õhus või maa sees olevate punktide koordinaatidele tuleks aga raadiuse väärtus juurde lisada. Polaarkoordinaate allpool näiteks elektroni orbitaalide kvantmehaaniliseks kirjeldamiseks vesiniku aatomis.
Liikumine, kiirus
Liikumine on keha asukoha (koordinaatide) muutumine ajas. Lihtsaim on ühtlane sirgjooneline liikumine: konstantsed on kiiruse absoluutväärtus ja suund.
Kiirus (v) on füüsikaline suurus, mida mõõdetakse ajaühikus läbitud teepikkusega. Teepikkus s on kahe asukoha vahekaugus. Kolmemõõtmelises ruumis avaldub teepikkus alg ja lõpp-punkti koordinaatide kaudu järgmiselt
![]() (1.1)
(1.1)
Pikkuse (teepikkuse) ühikuks on meeter, m. Meeter on ligilähedaselt 1/40000000 Maa ümbermõõtu, kuid täpne ühik on kokkuleppeline ja oli pikemat aega defineeritud kui kahe peene kriipsu vahe plaatina-iriidiumi sulamist siinil, mida hoiti Pariisi lähedal, nüüd aga on meeter seotud teatud aine aatomite poolt kiiratava valguse lainepikkusega. Meeter on üks kolmest põhiühikust ja teda ei saa tuletada teiste ühikute kaudu.
Kiirus
![]() ,
kust
,
kust ![]() ja
ja ![]() (1.2)
(1.2)
Viimased valemid seovad omavahel kiiruse, teepikkuse ja aja. Aja ühikuks on sekund, s. Sekund on ligilähedaselt 1/(365.25x24x60x60) keskmise astronoomilise ööpäeva pikkusest, kuid tema täpne väärtus on praegu seotud teatud aine poolt kiiratava valguse võnkeperioodiga. Sekund on üks kolmest põhiühikust ja teda ei saa tuletada teiste ühikute kaudu. Näiteks kiiruse ühik on m/s ehk m s-1 ja see on tuletatud põhiühikutest. Suurem osa tuletatud ühikuid on seotud põhiühikutega andes viimastele väärtuse 1.
Nii
teepikkus kui ka kiirus on vektorid, millel on x, y, ja z- suunalised
komponendid. Kahemõõtmelisel (tasapinnalisel juhul)
vektori s kaks komponenti on sx=scos;
sy=ssin![]()
Ebaühtlase liikumise kiirendus (a) on füüsikaline suurus, mida mõõdetakse kiiruse muutusega ajaühikus. Sirgjoonelise liikumise kiirendus on kiiruse muutumise kiirus, seega teine tuletis teepikkuse muutumisest:
![]() (1.3)
(1.3)
Ka kiirendus on vektor, s.t., valem (1.3) kehtib sx, sy ja sz suhtes eraldi. Kiirenduse ühik on m s-1 s-1 = m s-2 (loe: meeter sekundis sekundis).
Kiirendusega liikumise kiirus
![]() (1.4)
(1.4)
kui alghetkel kiirus ei olnud mitte null vaid v0.
Kiirendusega liikumisel läbitud teepikkus, kui aega hakkame lugema nullist (integraali alumine rada on null ja arvutada tuleb ainult ülemine rada):
![]() (1.5)
(1.5)
ja
teepikkuse s läbimiseks kuluv aeg 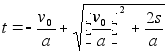 (1.4)
(1.4)
Juhul, kui algkiirus on null, siis
![]() , (1.5)
, (1.5)
kust leiame aja, mis kulub teepikkuse s läbimiseks:
![]() (1.6)
(1.6)
ja kiiruse v, mis saavutatakse teepikkuse s läbimisel
![]() (1.7)
(1.7)
Maa raskuskiirendus on g=9.81 m s-2 ja see määrab vabalt langevate kehade liikumise kiirenduse.
Ülesanded: Kuidas määrata torni kõrgust ampermeetri ja stopperi abil?
Kui suure algkiirusega peab pumpama vett, et purskkaevu juga kerkiks 30 m kõrgusele?
Kui kõrgele ja kui kaugele ulatub sama juga kui see suunata 45 kraadi all kaldu?
Kuidas peab piloot juhtima lennukit, et kabiinis tekiks kaaluta olek?
Vähemalt kui suure algkiirusega peab toimuma kaugushüppaja äratõuge ja missuguse nurga all tuleb see suunata, et püstitada uus maailmarekord (oletame, et praegune maailmarekord on 9 m)?
Ringikujulisel (elliptilisel) trajektooril liikuvate kehade orbiidi leidmiseks tutvume kõverjoonelise liikumise kiirendusega, millest lihtsaim on ringjooneline liikumine.
Kõverjoonelise (ringjoonelise) liikumise tangentsiaal- (puutujasuunaline) kiirus
![]() (1.8)
(1.8)
kus r on raadius, on tiirlemisperiood ja on tiirlemissagedus. Ristikiirendus
![]() (1.9)
(1.9)
kus on nurk-kiirus. Nurkkiirust mõõdetakse pöördenurga suurenemise kiiruse kaudu, ühik on radiaan sekundis. Täisring on 2 radiaani, seega üks tiir sekundis tähendab nurkkiirust 2 radiaani sekundis.
Dünaamika põhimõisted ja seadused: jõud, impulss, töö, energia
Newtoni esimene seadus (ka Galilei seadus, inertsiseadus): Iga keha liigub ühtlaselt ja sirgjooneliselt seni kuni teiste kehade mõju (jõud) ei põhjusta selle seisundi (kiiruse) muutumist.
Ühtlane ja sirgjooneline liikumine on võimalik ainult avakosmoses väga kaugel taevakehadest. Maa pinnal on kõik kehad gravitatsioonivälja mõjusfääris ja neile mõjub Maa külgetõmbejõud. Demonstratsioonkatseks on mõjudeta liikumisele ligilahedane teraskuuli veeremine horisontaalsel peegelpinnal, kus raskusjõud on liikumisega risti ja hõõrdumisjõud on minimaalne. Ka piljardikuulid liiguvad küllatki ühtlaselt ja sirgjooneliselt kuni põrkumiseni.
Newtoni teine seadus: Liikumise muutumise kiirus (kiirendus) on võrdeline rakendatud jõuga ja toimub jõu suunas.
![]() ehk
ehk
![]() (2.1)
(2.1)
kus f on jõud, m on keha mass ja a on kiirendus. Võrdetegur, mis seob kiirenduse jõuga on pöördvõrdeline keha massiga, s.t. üks ja seesama jõud põhjustab seda suurema kiirenduse mida väiksem on keha mass. Jõud f ja kiirendus a on vektorid (suunaga suurused), m on skaalar (suunata suurus). Massi ühik on kilogramm (kg). Üks kilogramm on ligilähedaselt ühe dm3 puhta vee mass, kuid täpne massi etaloon on plaatina-iriidiumi sulamist metallkeha, mis on hoiul Pariisi lähedal. Kilogramm on seega üks kolmest põhiühikust, mille suurus on kokkuleppeline ja mida ei saa tuletada teiste ühikute kaudu. Tuletatud ühiku näiteks on jõu ühik: üks njuuton (N) on jõud, mis annab massile üks kilogramm kiirenduse üks m s-2
Mass: kaal ja inerts
Massil on kaks omadust: inerts ja gravitatsioon. Huvitaval kombel on need kaks omadust alati võrdelised ja massi suurust saab määrata nii ühe kui teise kaudu. Kaalumine on massi mõõtmise viis gravitatsioonijõu kaudu. Mitu N kaalub keha massiga 1 kg? Kaal on raskusjõud, millega Maa tõmbab keha. Raskusjõud annab massile 1 kg kiirenduse 9.8 m s-2, sel ajal kui 1 N annab kiirenduse vaid 1 m s-2. Seega, mass 1 kg kaalub 9.8 N. Sama mass 1 kg kaaluks Kuu peal umbes kuus korda vähem, seega umbes 1.6 N. Keha kaal sõltub ka asukohast Maal (ekvaatoril on Maa pöörlemisest tulenev tsentrifugaaljõud suurem ja see vähendab kaalu). Kaalu vähendab ka õhu üleslüke. Seega, üks kilogramm udusulgi kaalub vähem kui 1 kg rauda, kui ei arvestata õhu üleslükke parandit. See parand on seda suurem, mida lähdasemad on kaalutava keha ja õhu tihedused, kuni selleni, et vesinikuga täidetud õhupall omab negatiivset kaalu. Õige kaalu määramine oleks õhu üleslüket arvestades, kuid praktikas, kui on tegu tahkete ainete või vedelikega, on selle tähtsus suhteliselt väike. Kui küsite poest ühe kg leiba, siis soovite te tõepoolest leiva massi, mitte selle kaalu. Seega küsimine kilogrammides ja mitte njuutonites on füüsikaliselt õige. Kui müüja kaalub leiva vedrukaaluga, siis saab ta tulemuse njuutonites ja see sõltub laiuskraadist. Kui aga kasutatakse kangkaalu, siis võrreldakse omavahel kaalutavat keha kaalupommide massiga ja tulemus ei sõltu laiuskraadist.
Newtoni kolmas seadus: Mõju (jõud) on
võrdne vastumõjuga (vastujõuga) ![]() .
Kui esimene keha mõjutab teist jõuga f siis
teine keha mõjutab esimest jõuga –f.
Klassikaline näide: paadist kaldale hüpates tõukate
paati kaldast eemale. Kumb aga liigub kiiremini, teie või
paat?
.
Kui esimene keha mõjutab teist jõuga f siis
teine keha mõjutab esimest jõuga –f.
Klassikaline näide: paadist kaldale hüpates tõukate
paati kaldast eemale. Kumb aga liigub kiiremini, teie või
paat?
Kahe keha vastasmõjul saavad mõlemad kiirenduse pöördvõrdeliselt nende kehade massiga:
![]() ehk
ehk
![]() (2.2)
(2.2)
Newtoni kolmandal seadusel põhineb rakettmootori töö. Igal ajamomendil paiskab reaktiivmootor suhteliselt väikest kütuse massi suure kiirendusega tahapoole, selle tulemusena liigub rakett kui suurem mass väiksema kiirendusega vastassuunas. Protsess on pidev seni kuni mootor töötab ja kuna kiirendus mõjub mõlemale, nii raketile kui kütusele võrdse aja jooksul, siis lõppkokkuvõttes suhtuvad ka raketi ja ruumi väljapaisatud kütusemassi kiirused nii nagu valem (2.2) näitab kiirenduste kohta. Kui näiteks raketi ja kütuse massid on võrdsed, siis on lõpuks võrdsed ja vastassuunalised ka nende kiirused. Erinevus raketi ja ruumipaisatud kütuse vahel on aga selles, et rakett kui tahke keha omab ühte kindlat kiirust, kütuse põlemisprodukt aga on gaasiline ja valem (2.2) kehtib selle ruumilise massikeskme kohta.
Ka lindude lendamine (ja isegi loomade või inimese ujumine) on
sisuliselt reaktiivliikumine, sest teist võimalust kui Newtoni
kolmanda seaduse abil õhust raskemal kehal õhus (veest
raskemal kehal vee peal) püsimiseks ei ole. Lind lükkab
tiibadega õhku allapoole, mõjutades õhumassi
jõuga ja andes õhule allapoole liikumise kiirenduse,
samal ajal vastujõud tõukab lindu ülespoole. Linnu
ülespoole liikumise kiirendus on niisama suur kui
raskuskiirendus, kuid sellega vastassuunaline, nii et mõlemad
kompenseeruvad ja lind lendab konstantsel kõrgusel. Matemaatiliselt,
![]() ,
kus m1 on linnu ja m2 tiibade all
liikuma pandud õhu mass ning a on viimasele antud
kiirendus.
,
kus m1 on linnu ja m2 tiibade all
liikuma pandud õhu mass ning a on viimasele antud
kiirendus.
Ülesanne: Selgitada, mis ühist on lennuki reaktiivmootoril, propellermootoril, lendamisel tiivalehvitamisega ja planeerimisel.
Üks tähtsamaid kiirendusest tulenevaid jõude on kesktõmbejõud ja kesktõukejõud ringlikumisel, mis on võrdsed javastassuunalised. Keha liigub ringikujulist trajektoori mööda tänu jõule, mis tõmbab teda keskpunkti suunas. Kesktõmbejõud võib olla gravitatsioon (Maa tiirlemine ükber Päikese), elektromagnetiline (elektroni tiirlemine ümber tuuma) või mehaaniline (nöör mis ühendab lingukivi käega, tsentrifugaalpumba korpus, mis suunab vedeliku ringtrajektoorile, aga ega nedes kehadeski esine lõppkokkuvõttes muud kui elektromagnetilised jõud). Kesktõukejõud tekib keha inersti tõttu, tema püüdest likuda sirgjooneliselt puutujat mööda. Kesktõukejõud ringliikumisel avaldub järgmiselt
![]() .
.
kus on nurkkiirus. Nurkkiirus seostub lineaarkiirusega järgmiselt:
![]() ehk
ehk ![]() ,
seega
,
seega
![]()
Kui suur on 100 kg-se mehe kaaluvahe poolusel ja ekvaatoril? Maakera raadius on 6000 km. Nurkkiirus on 2/(24x3600) = 7.27x10-5 radiaani sekundis. Asendades need värtused valemisse (??) saame f=100x(7.27x10-5)2x6x106 = 100x52.8x10-10x6x106= 3.168 N. Poolusel kaalub 100 kg 981 N. Suhteline kaalu kahanemine on 3.17/981=0.0032 ehk 0.32%. Meie laiuskraadil ja ekvaatoril on see suhe veel umbes poole väiksem.
Tsentrifugaaljõu praktilisi rakendusi: tsentrifugaalpumbad ja ventilaatorid. Kuidas muutub ventilaatori ja tsentrifugaalpumba arendatav rõhk mootori pööretest?
Liikumise hulk ehk impulss.
Kui püüate
väga massiivset keha, näiteks autot, liikuma lükata,
siis tuleb jõudu rakendada küllalt kaua, enne kui
saavutate vajaliku kiiruse, näiteks küllaldase mootori
käivitamiseks ilma starteri abita. See tähendab, et keha
poolt saavutatud kiirus sõltub jõu mõjumise
ajast. Kasutame kiiruse arvutamiseks kahte seost: ![]() ,
kust
,
kust ![]()
Suurust mv nimetatakse liikumise hulgaks ehk impulsiks. Impulsi muutus on võrdeline jõuga ja selle mõjumise ajaga ning toimub jõu suunas.
Impulsi jäävus liikuvate kehade vastasmõjudes on energia jäävuse kõrval üks looduse põhiseadusi. Näiteks kahe piljardikuuli põrkel või kahe gaasimolekuli põrkel
![]()
Impulsi muutus kehade vastasmõjul on võrdne ja vastassuunaline, süsteemi summaarne impulss on konstantne. Impulsi mõistet kasutame allpool gaaside rõhu arvutamisel.
Töö ja energia.
Töö on füüsikaline suurus, mida mõõdetakse jõu ja jõu suunas läbitud teepikkuse korrutisega
![]()
Töö ühik on Dzhaul (Joule), [J] = [N]x[m]. Dzhaul on töö, mida teeb jõud üks njuuton ühe meetri pikkusel teel. Tööd tehakse siis, kui liigutatakse mingit keha avaldades sellele jõudu. Näiteks, tõstes 50 kg viljakotti maast 1m kõrgusele vankrile tehakse töö mis võrdub koti kaal (njuutonites !) korda vankri kõrgus, 50x9.8x1=490 J. Kui vesi langeb 20 m kõrguses joas käivitades turbiini, siis iga kg vett teeb tööd 20x9.8=295 J.
Kui jõud on teepikkuse (koordinaadi) funktsioon (on muutuv sõltuvalt asukohast), siis tuleb rakendada integreerimist. Integreerida võib liikumise ja jõu kui vektori komponente kolme koordinaadi suunas eraldi
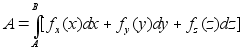
Tüüpiline muutuva jõu poolt tehtud töö arvutus on seotud keha asukoha muutusega teise keha gravitatsiooni- või elektriväljas. Näiteks, Newtoni gravitatsiooniseadus väidab, et kahe keha vahel mõjub gravitatsioonijõud, mis on võrdeline nende kehade masside korrutisega ja pöördvõrdeline nedevahelise kauguse ruuduga:
![]()
Elementaartöö, mida tehakse selleks, et suurendada kehade vahelist kaugust dx võrra oleks
![]()
ja liikumisel üle mingi pikema vahemiku tehtud töö oleks
![]()
![]()
Kui teepikkus on määratud, tuleb integraal võtta radades liikumise algpunktist lõpp-punkti. Valem ??? näitab, et kui kahe keha vaheline jõud kahaneb kauguse suurenedes pöördvõrdeliselt kauguse ruuduga, siis tehtud töö kasvab kauguse kasvades pöördvõrdeliselt kaugusega. Tõmbuvate kehade vahelise kauguse suurendamiseks tuleb teha välist tööd, kui kehad lähenevad, siis nad teevad ise tööd. Tõukuvate kehade, näiteks samanimeliste laengute vahel, on olukord vastupidine: tõukuvate kehade lähendamiseks tuleb teha välist tööd, kui need kehad eemalduvad teineteisest, siis nad teevad ise tööd. Viimase juhu näiteks oleks aatomite lähenemine, kus välise elektronkihi elektronid tõukuvad üksteise elektriväljas. Tahkete kehade kokkupuude ja hõõrdumine ongi väliste elektronkihtide tõukumine, tegelikku füüsilist kokkupuudet ei esine kunagi.
Võimsus on füüsikaline suurus, mida mõõdetakse ajaühikus tehtud töö hulgaga.
![]()
Võimsust kasutatakse näit. mootorite ja küttekehade hindamisel, teadmaks kui palju tööd need suudavad ajaühikus teha. Võimsuse ühik on Watt [W] = [J] [s]-1 üks Dzhaul sekundis. Elektripirnide tarbitav võimsus on näiteks 40 – 100 W, elektripliit 600 – 2000W, automootor 50 – 100 kW. Elektrienergia hulga mõõtmiseks kasutatakse ühikut kilovatt-tund (kWh), see on töö, mida teeb võimsus 1 kW ühe tunni = 3600 s jooksul. Üks kWh = 1000 J s-1 x 3600 s = 3600000 J = 3600 kJ.
Energia on keha võime teha tööd.
Energiat on kahte liiki, liikuva keha kineetiline energia ja jõuväljas asuva keha potentsiaalne energia. Energia jäävuse seadus on looduse põhiseadus: Energia ei teki ega kao, vaid muundub ühest vormist teise. Seega, looduses toimub kineetilise energia muundumine potentsiaalseks ja potentsiaalse energia muundumine kineetiliseks.
Liikuva keha kineetiline energia. Arvutame, kui palju tööd tuleb teha, et keha (massiga m) kiirust suurendada paigalseisust kuni väärtuseni v. See töö moodustabki likuva keha kineetilise energia.
Töö=energia: ![]()
Kui suur aga on teepikkus s mille lõpuks saavutatakse kiirus v? Kasutame seost (1.7)
![]() ,
kust
,
kust ![]()
Teades, et
![]() ,
asendame selle ja saame
,
asendame selle ja saame
![]()
Nüüd on selge, et
![]()
Kineetiline energia on võime teha tööd. Liikuva keha peatumisel võib ta enese ees lükata teist keha mõjudes sellele jõuga ja tehes tööd. Kui auto sõidab vastu puud, siis auto kineetiline energia liigutab plekke paigast ja murrab sõitjate luid. Tähelepanu, et auto kiiruse suurenemisel kaks korda suureneb kineetiline energia neli korda! Niisugustel deformeerivatel põrgetel muutub kineetiline energia peamiselt molekulide soojusenergiaks. Kineetiline energia muutub potentsiaalseks energiaks kui liikuvat keha peatab jõuväli, näiteks kui viskame kivi ülespoole. Gravitatsioonivälja jõud peatab lõpuks kivi liikumise, kuid kivi kineetiline energia on muundunud tema potentsiaalseks energiaks. Sama juhtub elektronidega, kui nad saavad lisaks kineetilist energiat (näiteks aatomite põrgetel või valguse neeldumisel): nad liiguvad tuumast kaugemale.
Jõuväljas asetseva keha potentsiaalne energia.Vaatleme esialgu gravitatsioonivälja maapinna lähedal. Arvutame, kui palju tööd tuleb teha keha (massiga m) tõstmiseks kõrgusele h.
![]()
Gravitatsiooniväli ja elektriväli on nn. potentsiaalsed väljad, kus keha potentsiaalse energia muutus sõltub ainult alg-ja lõppasukohast, mitte aga vahepealse liikumise trajektoorist. Tehtud töö on sama, ükskõik millist rada mööda liigutakse samade alg- ja lõpp-punktide vahel. Vabal inertsel liikumisel jõuväljas (ilma välismõjudeta) potentsiaalne ja kineetiline energia pidevalt muunduvad teineteiseks, nii et summaarne energia on kogu aeg sama:
![]()
Näiteks kõrguselt h kukkuva keha kiiruse leiame teades et kukkumise lõpuks
![]() ,
kust
,
kust ![]()
Ülesvisatava kivi maksimaalkõrguse võime samuti leida tema algenergia (algkiiruse) kaudu.
Kineetilise ja potentsiaalse energia muundumine toimub ka lihastetöös. Näiteks võib teoreetiliselt arvutada, kui kõrgele saab hüpata kirp, kelle kehas keskmine ATP kontsentratsioon on 0.1 mM, eeldades, et ATP keemiline energia kõik muutub hüppel kineetiliseks energiaks.
Eelmised ülesanded on lihtsad, sest ülesvisatud keha kõrgus muutub suhteliselt Maa raadiusega sedavõrd vähe, et rakusjõudu saab lugeda konstantseks. Kui aga kaugus muutub suhteliselt palju, näiteks nagu kosmoselendudel, või nagu elektroni kaugus muutub tuuma suhtes, siis ei saa ei gravitatsiooni- ega elektrivälja jõudu enam konstantseks lugeda vaid töö (energia) arvutamisel tuleb arvestada, et jõud muutub koos kaugusega.
Jõudude tasakaal, kiirus ja energia ringjoonelisel tiirlemisel.
Looduses asuvad kõik kehad üksteise jõuväljades, suuremad kehad gravitatsiooniväljas, väikeste kehade puhul on oluline elektriväli. Ometi ei kuku tõmbuvad kehad üksteise peale, sest sellisel juhul oleks kogu Universum ammu kokku kukkunud, elektronid oleksid kukkunud aatomituumadesse ja planeedid nende Päikestesse. Loodust stabiliseerib see, et kehad tiirlevad üksteise ümber, nii et kesktõmbejõud ja kesktõukejõud on võrdsed ja radiaalsuunalist kiirendust (jõudu) ei esine. Kasutades füüsikast teadaolevaid valemeid gravitatsioonilise (elektrilise) kesktõmbejõu ja inertsiaalse kesktõukejõu kohta saab nende tasakaalutingimustest tuletada näiteks kui suur on tiirleva keha potentsiaalne, kineetiline ja summaarne energia.
Mõlemad, nii elektrivälja kui ka gravitatsioonivälja tugevus (mõjuv jõud) kirjelduvad ühe ja sellesama seadusega:
gravitatsiooniväli: ![]() ja elektriväli:
ja elektriväli:
![]()
kus m on keha mass, e on keha laeng (indeksid näitavad esimese ja teise keha oma eraldi), r on nendevaheline kaugus ka konstant k määrab seose kasutatava ühikute süsteemiga. Kui masse mõõdetakse kilogrammides, siis gravitatsioonijõu saamiseks Njuutonites omab gravitatsioonikonstant kg väärtust ????. Kui laenguid mõõdetakse Coulombides (Kulonites, C) siis elektrostaatilise tõmbejõu saamiseks Njuutonites elektriväljakonstant ke omab väärtust ????.
Muide, selles, et need konstandid ei oma väärtust 1, väljendub füüsikalise mõõtühikute süsteemi ajalooliselt kujunenud ebajärjekindlus. Süsteemselt õige oleks olnud massiühikuks võtta niisugune mass, mis teist samasugust tõmbab ühe pikkusühiku kauguselt ühikulise jõuga. Seesama ühikuline jõud aga peab andma ühikulisele massile ka ühikulise kiirenduse. Et see aga nii tuleks, peaks nii massi, pikkuse kui ajaühikut vastavalt muutma. Praegused põhiühikud ei ole üldse seotud gravitatsiooniseadusega. Samasugune on lugu elektrilaenguühikutega. Formaalselt peaks laenguühik Coulomb (Kulon) olema defineeritud kui laeng mis tõmbab teist samasuurt vastasmärgilist laengut pikkusühiku kauguselt ühikulise jõuga. Tegelikult on aga Coulomb defineeritud hoopis magnetvälja kaudu: Coulomb on laeng, mis liikudes ühe sekundi jooksul läbi 1 m pikkuse traadi mõjutab teist samasugust traati, milles voolab niisama tugev vool, 1 m kauguselt jõuga 1 N. See definitsioon baseerub magnetväljal, mis on liikuvate laengute ümber ruumis. Elektrivälja jõud avaldub nüüd aga ülaltoodud kaliibrimiskonstandi kaudu.
Leiame keha (laengu) potentsiaalse energia tsentraalsümmeetrilises gravitatsiooni- (elektri-) väljas. Kuna jõud on tugevasti kaugusest sõltuv, siis tuleb kindlasti rakendada integreerimist. Laengu liikumisel elektriväljas väga lühikesel teepikkusel tehtud töö on
![]()
![]()
kus liikumise teepikkust tähistame seekod raadiuse (kugus tsentrist) muutusena dr. Kui laeng liigub raadiuselt r1 raadiusele r2, peame integreerima vastavates radades:
![]()
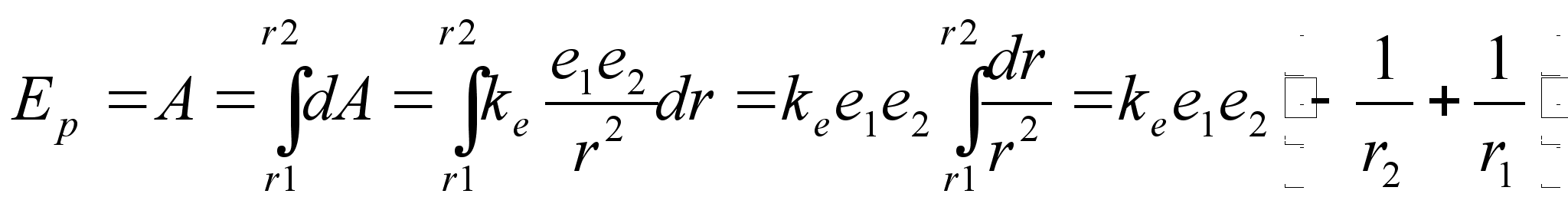
Valem
näitab, et tsentraalsümmeetrilises elektriväljas
liikudes muutub laengu potentsiaalne energia pöördvõrdeliselt
kaugusega tsentrist. Analoogiline valem kehtib ka gravitatsioonivälja
kohta, ainult et seal esinevad kahe laengu asemel kaks massi ja
elektrivälja konstandi asemel gravitatsioonikonstant. Kui laeng
liigub tsentrist eemale, siis r2>r1
ja negatiivne liige on väiksemkui positiivne,
seega siis potentsiaalne energia kasvab. Vastupidi, potentsiaalne
energia kahaneb, kui laeng liigub tsentrile lähemale.
Potentsiaalse energia nullnivoo on aga kokkuleppeline. See võiks
olla üks äärmuslikest seisunditest, kas ![]() või
või
![]() (lõpmatus). Siiski, raadius ei saa olla null, sest siis
läheneb energia lõpmatusele, seega jääb
kokkuleppeliseks nulliks nivoo, kus laengud asetsevad teineteisest
lõpmatu kaugel. Lähenedes aga nende potentsiaalne energia
kahaneb, seega muutub negatiivseks, ja läheneb miinus
lõpmatusele kui laengud kohtuvad. Niisugune potentsiaalse
energia nullnivoo definitsioon, mis on hea elektronide ja tuumade
vahelise mõju kirjeldamiseks aatomites, on erinev
igapäevakogemusest gravitatsioonilise energiaga, kus nulliks
loeme tavaliselt energia maapinnal ja energia loeme positiivselt
kasvavaks kui keha maapinnast kaugeneb. Kui valemis ???
(lõpmatus). Siiski, raadius ei saa olla null, sest siis
läheneb energia lõpmatusele, seega jääb
kokkuleppeliseks nulliks nivoo, kus laengud asetsevad teineteisest
lõpmatu kaugel. Lähenedes aga nende potentsiaalne energia
kahaneb, seega muutub negatiivseks, ja läheneb miinus
lõpmatusele kui laengud kohtuvad. Niisugune potentsiaalse
energia nullnivoo definitsioon, mis on hea elektronide ja tuumade
vahelise mõju kirjeldamiseks aatomites, on erinev
igapäevakogemusest gravitatsioonilise energiaga, kus nulliks
loeme tavaliselt energia maapinnal ja energia loeme positiivselt
kasvavaks kui keha maapinnast kaugeneb. Kui valemis ??? ![]() ,
st. elektron läheneb tuumale lõpmatu kaugelt, siis tema
potentsiaalne energia on alguses null ja kahaneb lõpuks
väärtusele
,
st. elektron läheneb tuumale lõpmatu kaugelt, siis tema
potentsiaalne energia on alguses null ja kahaneb lõpuks
väärtusele
![]()
![]()
![]()
Kuna see energia kuhugi kaduda ei saa, siis muutub ta elektroni liikumise kineetiliseks energiaks, st., lähenedes tuumale elektron liigub kiirenevalt, nii nagu näiteks asteroid liigub kiirenevalt lähenedes Maa pinnale. Vahe on siiski selles, et elektron ei lange kunagi tuumale, vaid jääb tiirlema mingil kaugusel ümber tuuma. Tiirlemise kaugus (raadius, on määratud sellega, millal elektriline tõmbejõud võrdub inertsiaalse kesktõukejõuga. Matemaatiliselt avaldub see tingimus järgmiselt:
![]()
Selle valemi vasak pool on varasemast tuttav kesktõukejõu valem keha massiga m ringliikumisel joonkiirusega v ümber tsentri kaugusel r. Valemi parem pool on elektrostaatilise tõmbejõu valem, kuid siin on juba arvestatud, et aatomis positiivne ja negatiivne laeng on võrdsed, mõlemad väärtusega e.
Eelmisest valemist saab leida raadiuse, mille saab siduda nii elektroni kiiruse kui tema kineetilise energiaga:
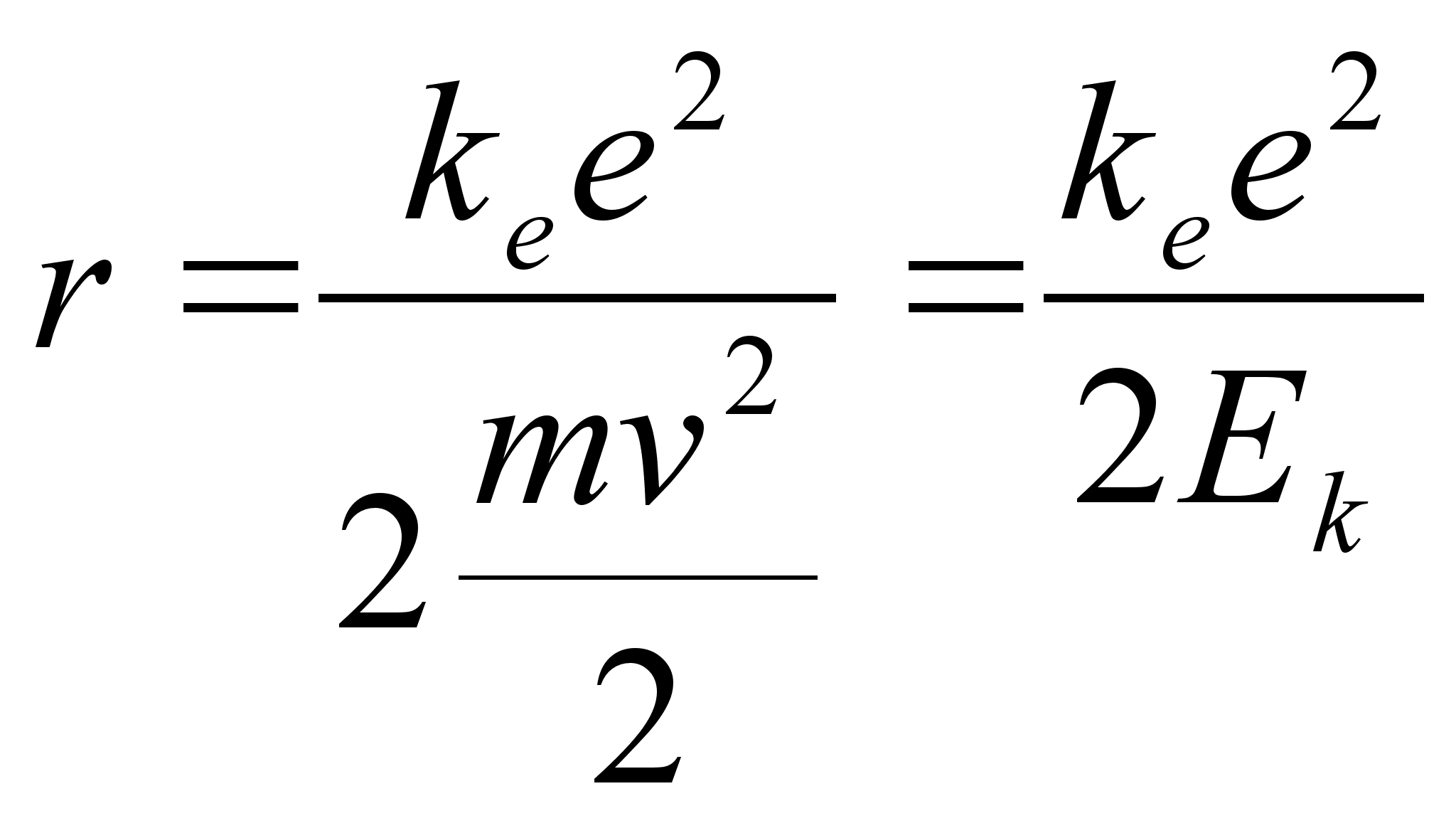
või
![]()
Ümber tuuma tiirleva elektroni kineetiline energia kasvab kui elektron läheneb tuumale (r kahaneb). Tuletame meelde, et potentsiaalne energia samal ajal kahanes:
![]() ,
,
ja summaarne energia
![]()
Elektroni summaarne energia kahaneb kui elektron asub tiirlema orbiidile mis on tuumale lähemal. Kuhu see energiavahe siis läheb, millisesse vormi muutub (kaduda ju ei saa)?
See energiavahe peab aatomist eralduma ja seda ta ka teeb, kas valguskvandi kujul, või kandub üle mõnele naaberaatomile, tõstes selle elektroni vastavalt kõrgemale energianivoole, või eraldub soojusena, s.o. muutub aatomi translatoorseks (kulgevaks) liikumiseks. Niisugune elektronide ja tuuma vahelise kauguse muutumine, elektronide tiirlemine erineva raadiusega orbiitidel, on peamine keemiliste ainete siseenergia, keemilise energia olemus. Ained, mille molekulides elektronid tiirlevad tuumadest kaugemal, on energiarikkamad ja võivad seda vabastada kui keemilise reaktsiooni tulemusena toimuvad muutused, mille tulemusena elektronid saavad tuumadele lähemale asuda. Bioloogiliste protsesside energeetika on samadel alustel: fotosünteesis tõstetakse elektron valguskvandi abil kõrgemale energianivoole, tuumast kaugemale orbiidile, ja metabolismi käigus ta järkjärgult läheneb tuumale, vabastades niimoodi kvandi poolt talle antud energia.
Kas aga elektronid saavad tiirelda ümber tuuma igasugustel kaugustel? Kui see nii oleks, võiks ju vabastada väga suuri keemilise siseenegia koguseid lubades elektronil asuda tuumale väga-väga lähedale (lastes raadiuse nulli lähedale). Tõepoolest, klassikaline füüsika seda lubaks, kuid tegelikkuses seda ei juhtu. Siin tulevad sisse kvantmehaanilised piirangud, mis klassikalise füüsika abil ei seletu. Järgnevas tutvumegi atomaarse kvantteooria põhialustega.
BOHRI AATOMIMUDEL
Eelmises lõigus tuletasime valemid, mis kirjeldavad ümber tuuma tiirleva elektroni kiirust ja energiat. Igale elektroni kineetilise energia väärtusele Ek vastaks kindel raadius r. Klassikalise füüsika seisukohtade kohaselt tekitab aga tiirlev elektron muutuva elektromagnetilise välja: elektron on perioodiliselt kord tuumast parmal, siis jälle vasemal, seega ‘pluss’ ja ‘miinus’ vahelduvad nagu televisiooni saateantenni varrastes, vahe on ainult mõõdus ja tiirlemise sageduses. Muutuva elektromagnetilise välja kaudu peaks elektroni tiirlemisenergia välja kiirguma, elektron peaks tuumale lähenema ja lõpuks tuumale kukkuma. Tegelikult seda ei toimu, kõik aatomid maailmas on stabiilsed ja tavaliselt ei kiirga energiat. Selles on klassikalise mehhaanika põhivastuolu tegelikkusega. Seda vastuolu ei saa eletada, see tuleb lihtsalt teadmiseks võtta ja postuleerida, et teatud kindlate energiaväärtuste puhul on elektronide orbiidid aatomis stabiilsed ja energiat ei kiirgu, kuigi põhjus, miks ei kiirgu, ei ole teada. Kui see aga teadmiseks võtta, siis saab sellele üles ehitada uut sorti mehanika – kvantmehaanika. Esimeseses järjekorras tuleb postuleerida, missugused on need orbiidid, millel elektron saab stabiilselt tiirelda ilma energiat kiirgamata.
Uurides kuumutatud kehadelt kiirguva valguse spektreid leidis Max
Planck (1900) ka siin vastuolu, mis lahenes, kui eeldati, et valgusel
on kvantiseloom: valgus kiirgub energiaportsjonite e. kvantide kaupa,
millest igaühe energia ![]() ,
kus on valguslaine
võnkumise sagedus.
,
kus on valguslaine
võnkumise sagedus.
Lähtudes sellest postuleeris Bohr (1913): elektroni tiirlemisel ümber tuuma elektrmagnetilist lainet (=valgust) ei kiirgu, kui elektron tiirleb orbiitidel millel potentsiaalne on
![]() .
.
Kineetiline energia oli positiivne ja pool potentsiaalsest energiast:
![]() ,
,
Nendes valemites on elektroni tiirlemise sagedus, n aga mingi täisarv 1, 2, 3, 4 jne.
Kasutades seost joonkiiruse ja nurkkiiruse vahel, mille abil sagedus teisendatakse joonkiiruseks, saame:
![]() ja
ja
![]()
ja võime kirjutada
![]()
ehk
![]()
või võttes mõlemad pooled ruutu saame:
![]() .
.
Elektrostaatilise tõmbejõu valemist (???) saame massiga m läbi korrutades:
![]()
Kahe viimase valemi vasakud pooled on võrdsed. Paremate poolte võrdsustamisel saame avaldada lubatud raadiuse
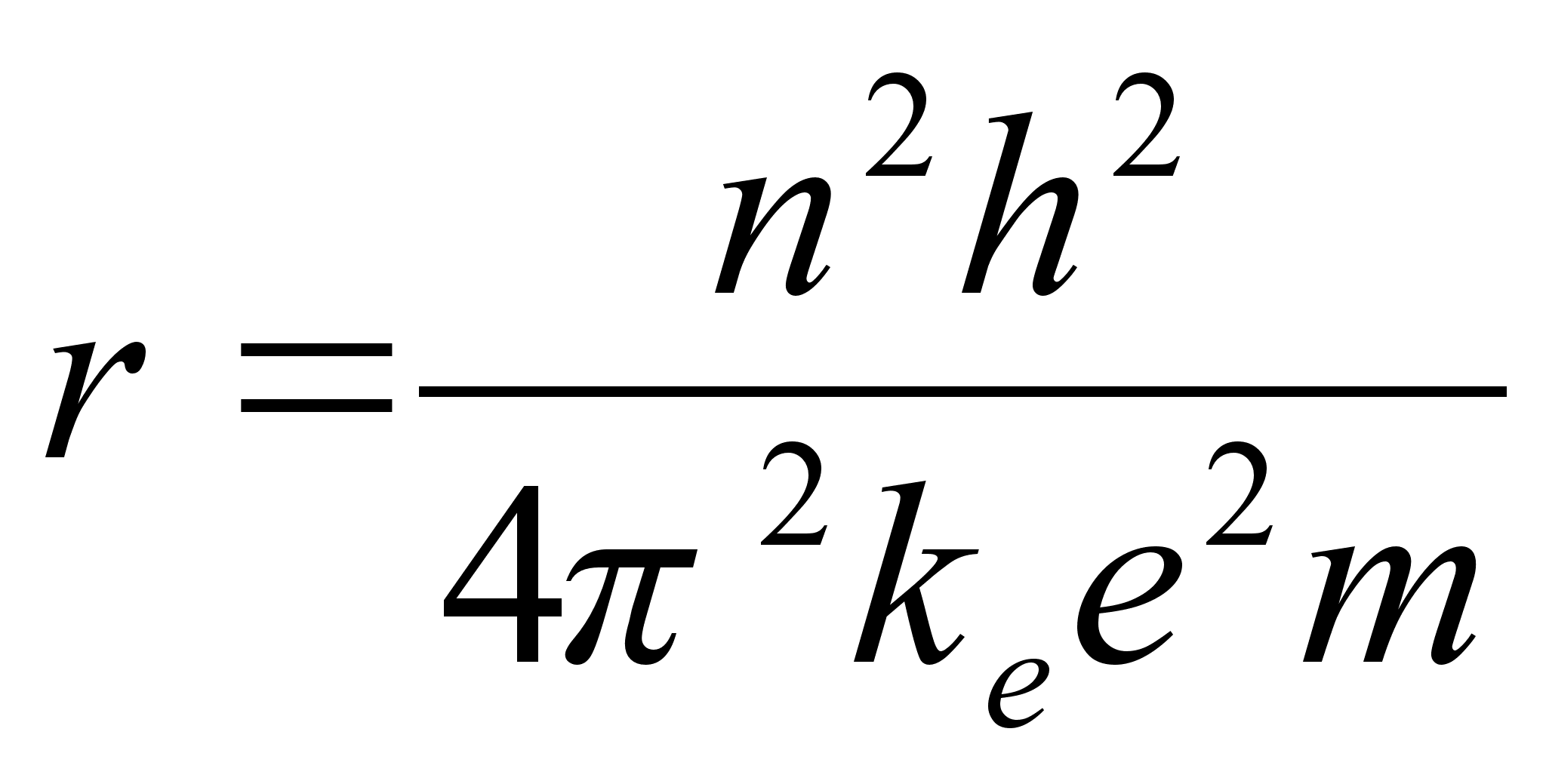 .
.
Need nn. Bohri raadiused ongi võimalikud raadiused millel elektron saab asuda stabiilselt ilma energiat kiirgamata.
Avaldame elektroni kineetilise energia tema massi m ja laengu e kaudu. Selleks asendame r valemisse (???) või (???). Saame
![]()
Samale orbiidile vastav potentsiaalne energia
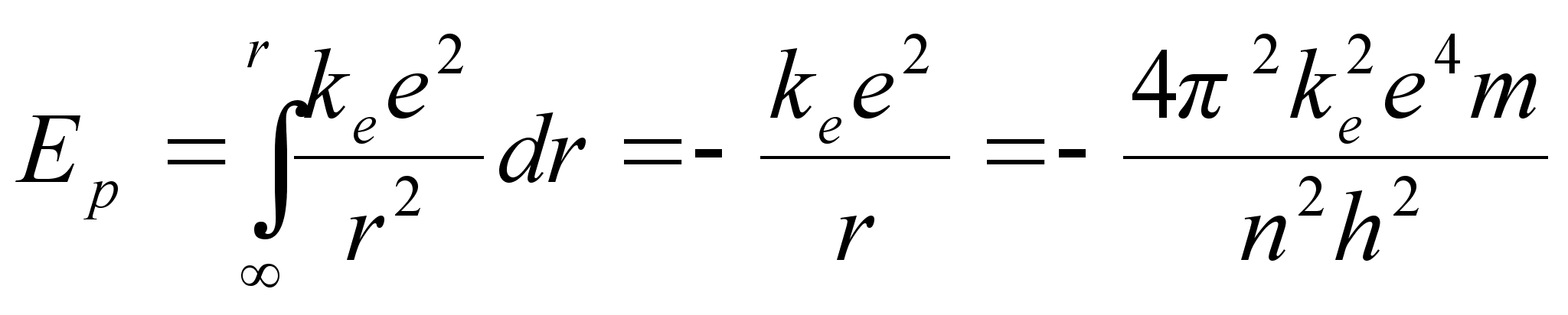
ja koguenergia, mis vastab orbiidile, mida iseloomustab täisarv n
![]()
Võimalike naaberorbiitide energiate vahe
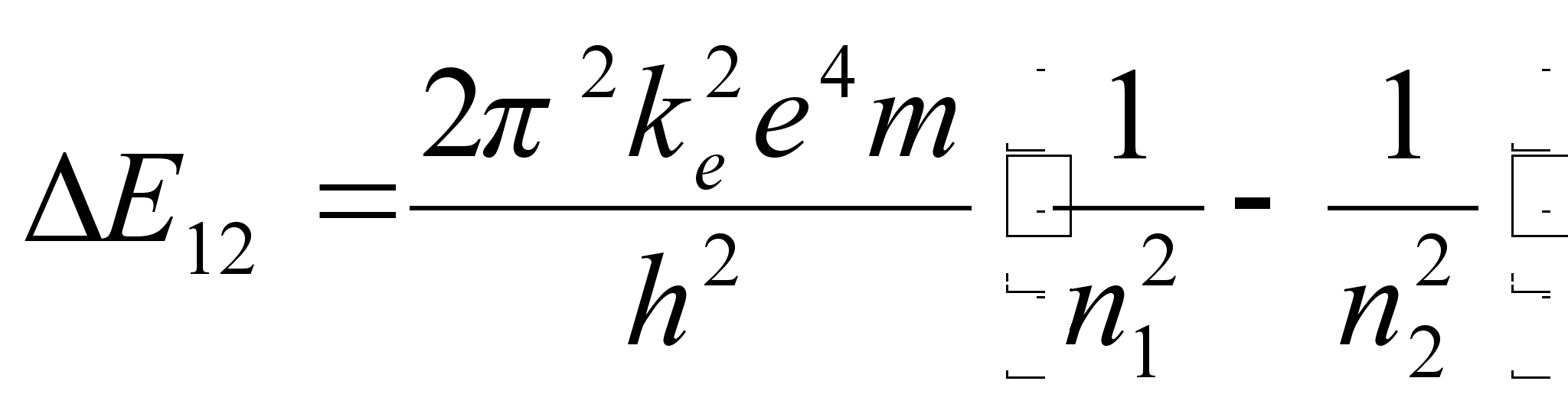
Elektroni tiirlemissageduste vahe kahel naaberorbiidil võrdub väljakiiratava (või neelatava) valguse sagedusega kahe orbiidi vahelisel üleminekul:
![]()
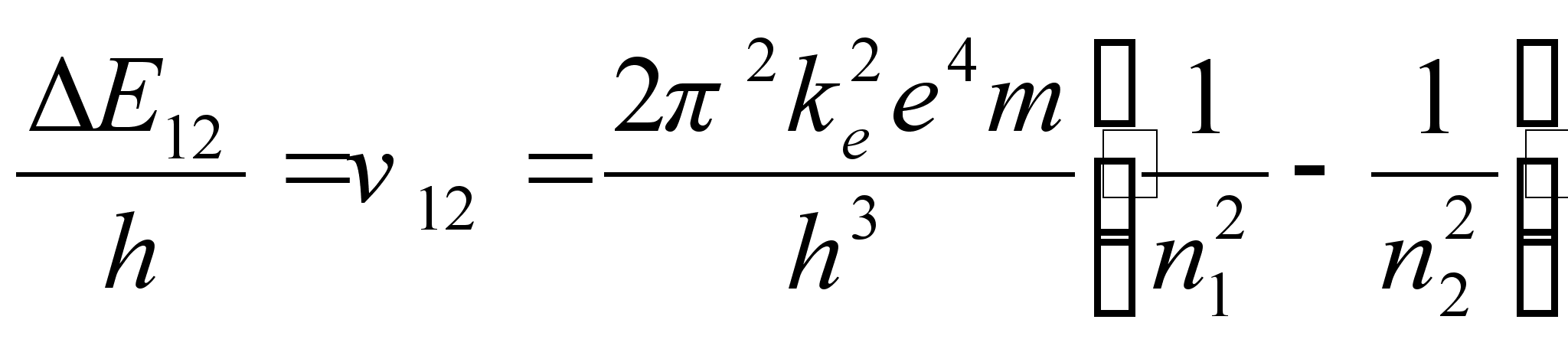 ja lainepikkus
ja lainepikkus ![]() kus c on valguse kiirus.
kus c on valguse kiirus.
Arvulisi andmeid: e = 1. 6021892·10-19 kulonit; h= 6.626176·10-34 J·s; me = 9.109534·10-31 kg
c = 299792458 m s-1 ke=???
Valem (???) näitab, et elektroni võimalikud tiirlemisraadiused suurenevad võrdeliselt täisarvude ruutudega, seega jada on 1, 4, 9, 16, 25, 36 ...
Valem (???) näitab,et elektroni koguenergia võimalikel orbiitidel suureneb raadiuse kasvades pöördvõrdeliselt täisarvu n ruuduga, seega jada oleks
![]()
Kõige sügavama energianivoo (põhinivoo) väärtus on vesiniku aatomis -13.6 eV, nivoode jada elektronvoltides oleks siis
-13.6; -3.4; -1.5; -0.85; -0.54; -0.38 ...eV
Volt (Itaalia teadlase Volta nimest) on elektrivälja potentsiaali (potentsiaalse energia) ühik. Elektrivälja kahe punkti potentsiaalide vahe on üks Volt kui laengu üks kulon viimisel ühest punktist teise tehakse tööd üks J. Ühe elektroni viimisel läbi potentsiaalide vahe üks volt tehakse tööd üks elektronvolt. Energeetiliselt elektronvolt on dzhaulist niisama palju kordi väiksem kui elektroni laeng on väiksem kulonist, seega 1 eV = 1. 6021892·10-19 J.
Orbiitide ja energianivoode joonised.
Nähtav ja nähtamatu elektromagnetiline kiirgus, valgus.
Energianivoode-vahelisel üleminekul kiiratakse kvant kui üleminek toimub tuumale lähemale ja neelatakse kvant kui üleminek toimub tuumast kaugemale. Kvandi energia on niisama suur kui vastavate orbiitide energianivoode vahe. Võtame teadmiseks, et vesiniku sügavaimale energianivoole vastab 13.6 eV ja arvutame sellele üleminekule vastava lainepikkuse.
![]()
See on silmale nähtamatu lühilaineline ultraviolett-kiirgus. Silm näeb ‘valgust’, mis on defineeritud kui elektromagnetiline kiirgus lainepikkuste vahemikus 400-700 nm ehk kvandi energiavahemik 3.10 kuni 1.77 eV. Vesiniku aatomisisestest üleminekutest kiirguks nähtavat kiirgust üleminekutel kõrgematelt nivoodelt teisele nivoole, teiselt esimesele nivoole üleminek kiirgab kvandi lainepikkusega 121.7 nm.
Seega, valguse ja sellest lühemate lainepikkustega kvandid kiirguvad elektroni üleminekul kõrgema energiaga orbiidilt madalama energiaga orbiidile, energiavahe kiirgub kvandina. Ka vastupidine protsess, kvandi neeldumine aatomis põhjustades elektroni ülemineku madalamalt orbiidilt kõrgemale, on võimalik. Nagu vesiniku aatomi analüüs näitas, on lubatud täiesti kindlad energianivood, seega niisuguses aatomis kiirguvad ja neelduvad ainult väga täpselt määratud lainepikkustega kvandid. Vesiniku aatomis on põhinivoo nii sügaval, et sinna üleminekul saavad kiirguda vaid ultraviolett-kvandid. Paljelektroniliste aatomite väliste kihtide lubatud põhinivood ei asu mitte nii sügaval ja neis kiirguvad/neelduvad ka nähtava valguse kvandid. Näiteks, tihti kasutatakse elavhõbe-auru ja naatriumi-auruga täidetud lampe, kus elektrienergia abil sunnitakse metalliaatomeid kiirgama nähtavat valgust. Kui aatomid asuvad gaasis tihedalt lähestikku, siis nad põrkuvad soojusliikumise tõttu ja need põrked moonutavad orbiitide kuju. Tulemusena nihkub igas moonutatud orbiidiga aatomis energianivoo veidi ja kogu gaas ei kiirga enam mitte joonspektrit teatud kindlate lainepikkustega, vaid nn. ribaspektrit, kus jooned on laienenud ribadeks.
Joonis: ribaspektri näidis kõrgrõhu elvhõbeauru-lambis.
Tahkes kehas asuvad aatomid nii tihedasti koos, et iga üksiku aatomi energianivoo muutub väga ebamääraseks. Kui tahket keha, näiteks metalli või sütt kuumutada, siis see hakkab valgust kiirgama. Madalamal temperatuuril on see kiirgus pikemalainelisem, nähtavaks muutub see tumepunasena kusagil 600 °C juures. Temperatuuri edasisel tõstmisel hakkab domineerima järjest lühemalainelisem kiirgus, muutudes silmale nähtavalt kollakaks, valgeks (nagu Päike) või isegi sinakaks (nagu kuumad tähed). Niisugustes kuumutatud tahketes kehades on kiirguse energiaallikaks aatomite (molekulide) soojusliikumine, mis põrgetel ‘ergastab’ elektrone, lükates neid ajutiselt kõrgematele niivoodele, kust nad siis kohe jälle alla kukuvad, kiirates kvante. Kuna aatomid asuvad väga tihedalt, siis on ka lubatud energianiivood väga tihedalt ligistikku, nii et igasuguse energiaga kvantide kiirgumine on võimalik. Sellest tulenevalt on kuumutatud tahkete kehade kiirgus pideva spektriga. Kuumutatud gaasides aga kiirgub ikkagi joon- või ribaspekter. Nagu öeldud, on madala temperatuuriga kehades lühilaineliste (kõrge energiaga) kvantide kiirgumine vähetõenäone ja neis domineerivad pikemalainelised kvandid. Näiteks Maa keskmine temperatuur on umbes 290 °K ja Maa kiirgab kosmosesse infrapunast kiirgust lainepikkuse maksimumiga umbes 10 m. Seevastu Päikese temperatuur on umbes 6000 °K ja tema kiirgusmaksimum on 0.5 m lainepikkuse juures. Hõõglampide niidi temperatuur on umbes 2000-3000 °K ja kiirgusmaksimum umbes 1 m juures. Nagu näeme, on silm kohastunud nägema just selles spektripiirkonnas, kus Päike kiirgab maksimaalselt. Seevastu hõõglampide spektrist suurt osa silm ei näe. Sellepärast ongi hõõglampide valgusviljakus (valguslik kasutegur) suhteliselt madal (10-20%).
Joonised: Päikese ja hõõglampide spektri näited.
Mateeria lainelised omadused: kvantmehaanika kui lainemehaanika
Uurides musta tahke keha kiirgusspektrit leidis Max Planck (1900), et see vastab energia juhuslikule jaotusele ainult tingimusel, et mitte igasugune kiirgumine ei ole võimalik, vaid ainult kiirgumine portsjonite, kvantide kaupa, mille igaühe energia ja võnkesagedus on seotud järgmiselt:
![]()
kus on võnkesagedus ja h nn. Planck’i konstant, mis on üks looduse universaalsetest konstantidest. Veidi hiljem leidis Alber Einstein oma üldrelatiivsusteooriast et elementaarosakeste (prootonite, elektronide jne.) mass ja energia on omavahel seotud:
![]()
kus c on valguse kiirus. Nendest kahest valemist järgneb, et kvandil (footonil) kui elektromagnetiliste lainete ‘paketil’ peab siiski olema ka mingi mass
![]() .
.
Seega on footon kahesuguste omaduste, nii lainepakett kui ka massiga osakene. De Brouglie (1927) arendas seda mõtet edasi, et absoluutselt iga osakene, millel on mass, omab samaaegselt ka lainelisi omadusi. Kui eelmine valem teisendada, saame
![]() ,
,
kust
![]()
See valem on kirjutatud footonite jaoks, mis alati liiguvad kiirusega c ja ei saa kunagi liikuda väiksema kiiruega. De Brouglie aga oletas, et massi ja lainepikkust siduv valem kehtib iga osakese kohta, ka nende kohta, mis võivad seista paigal või liikuda valguse kiirusest väiksema kiirusega. Sellisel juhul valem sisaldaks valguse kiiruse asemel osakese (keha) tegelikku kiirust
![]()
Vaatame, mida see hüpotees tähendaks Bohri aatomimudelis tiirleva elektroni kohta, milline oleks selle ‘lainepikkus”?
Elektroni kineetiline energia orbiidil, millele vastas täisarv n oli
![]()
Avaldades siit kiiruse v saame
![]()
ja vastava elektroni lainepikkuse
![]()
Võrdleme elektroni lainepikkust Bohri raadiusega
![]()
ehk
![]()
Viimases valemis lisasime raadiusele indeksi n näitamaks, et tegu on just nimelt täisarvule n vastava raadiusega. Valem ise aga näitab, et täisarvule n vastavale orbiidile mahub just nimelt n täislainet. Tuletame meelde, et kõrgemal orbiidil on elektroni kiirus väiksem, seega lainepikkus suurem. Siit järeldub, et orbiidi ümbermõõt (ka raadius) suureneb kahel põhjusel: elektroni lainepikkus suureneb ja orbiidile paigutatavate lainete arv ka suureneb. Siit tulenebki väliste orbiitide läbimõõdu kiire kasvamine kui elektroni summaarne energia hakkab nullile lähenema (elektron kaugeneb tuumast väga kaugele).
Lainemehaanika algmed
Lained on ruumis edasilevivad võnkumised. Edasilevimine tuleb sellest, et mingis ruumipunktis toimuv muutus kutsub esile sarnase muutuse naaberpunktis, aga veidi hiljem. Elektroni orbiidil ringlevad samuti lained, kuid kummas suunas? Et eelissuunda ei ole, siis levivad lained mõlemas suunas liikudes vastamisi. Kui seejuures on veel orbiidil täisarv laineid, siis tekib resultatiivselt nagu laine seiskumine, vastassuunalised levimised kompenseeruvad. Seega, elektron aatomi orbiidil moodustab seisva laine. Üldse, madalama potentsiaalse energiaga ruumiosas kinnihoitavad lained moodustavad alati seisvad lained, ja seda madalama potentsiaaliga ruumiosa kutsutakse ‘potentsiaaliauguks’. Gravitatsiooniväljas on kahemõõtmeline potentsiaaliauk näiteks kaev, kus ergastatud lained peegelduvad kaevu seintelt ja moodustavad veepinnal seisvaid laineid. Kolmemõõtmeline elektripotentsiaali auk on näiteks tuuma ümbrus, mis hoiab elektrone kinni kui seisvaid laineid. Seisvat lainet kirjeldav matemaatika on lihtsam kui levivat lainet kirjeldav, sest ajalisi muutusi ei esine ja vastav diferentsiaalvõrrand aega ei sisalda.
Juba varem leidsime, et võnkumiste võrrand on teist järku diferentsiaalvõrrand. Näiteks massi ajaliste võnkumiste jaoks oli põhiprintsiip, et tasakaalu poole suunatud jõud on võrdeline hälbega tasakaalupunktist, seega kiirendus on võrdeline hälbega tasakaalupunktist. Ruumilise võrrandi põhimõte on sama, ainult jõu ja kiirenduse mõistet siin kasutada ei saa:
![]()
Võrrand on ühemõõtmeline, kus mingi suurus A lainetab x-telje suunas. Kui lainetus võib esineda kolmes ruumisuunas, siis kirjutatakse lainefunktsiooni lühidalt
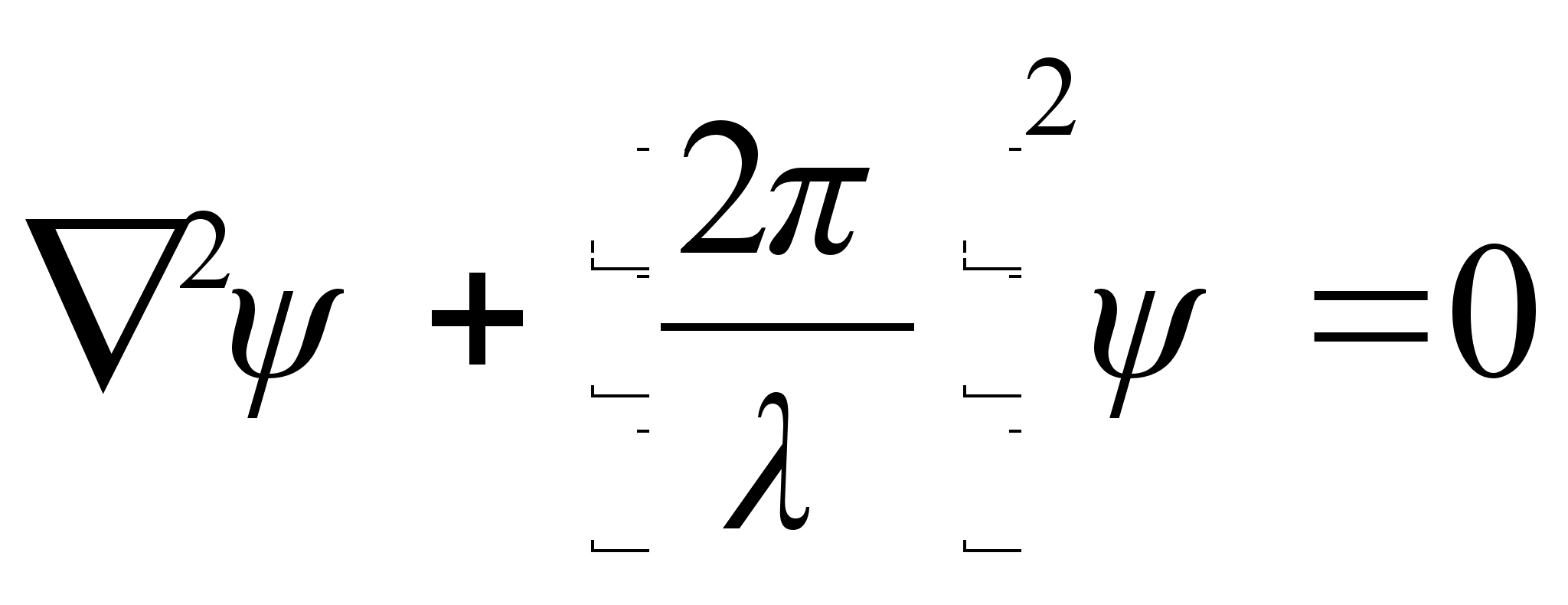 ,
kus
,
kus 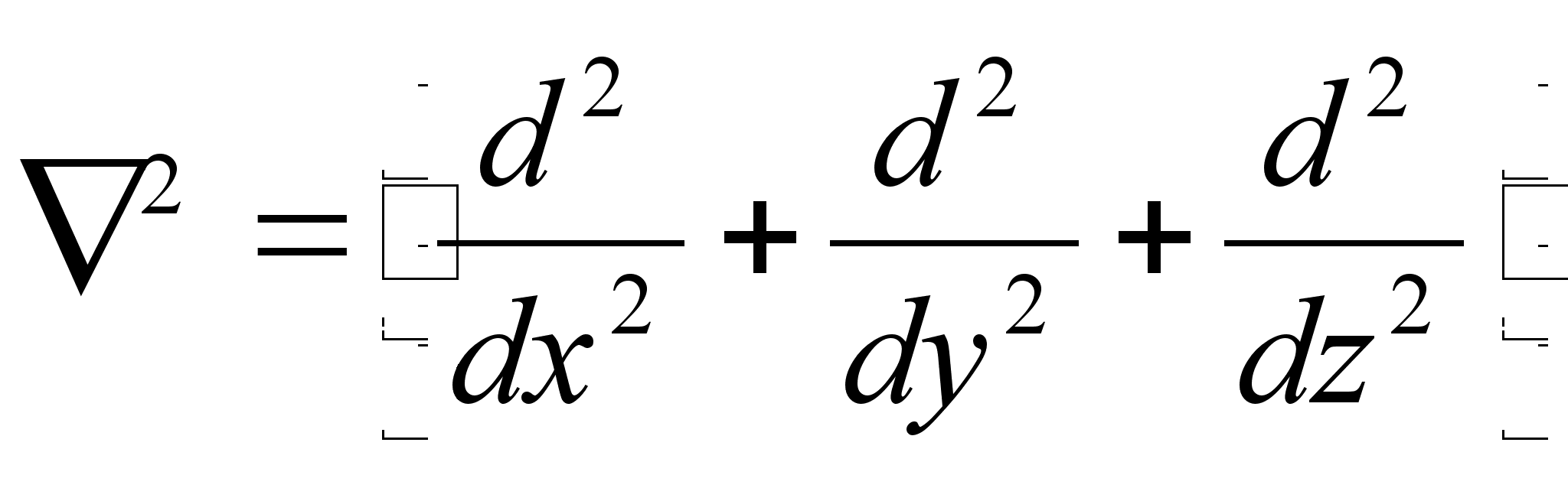
Asendades
![]() saame
saame
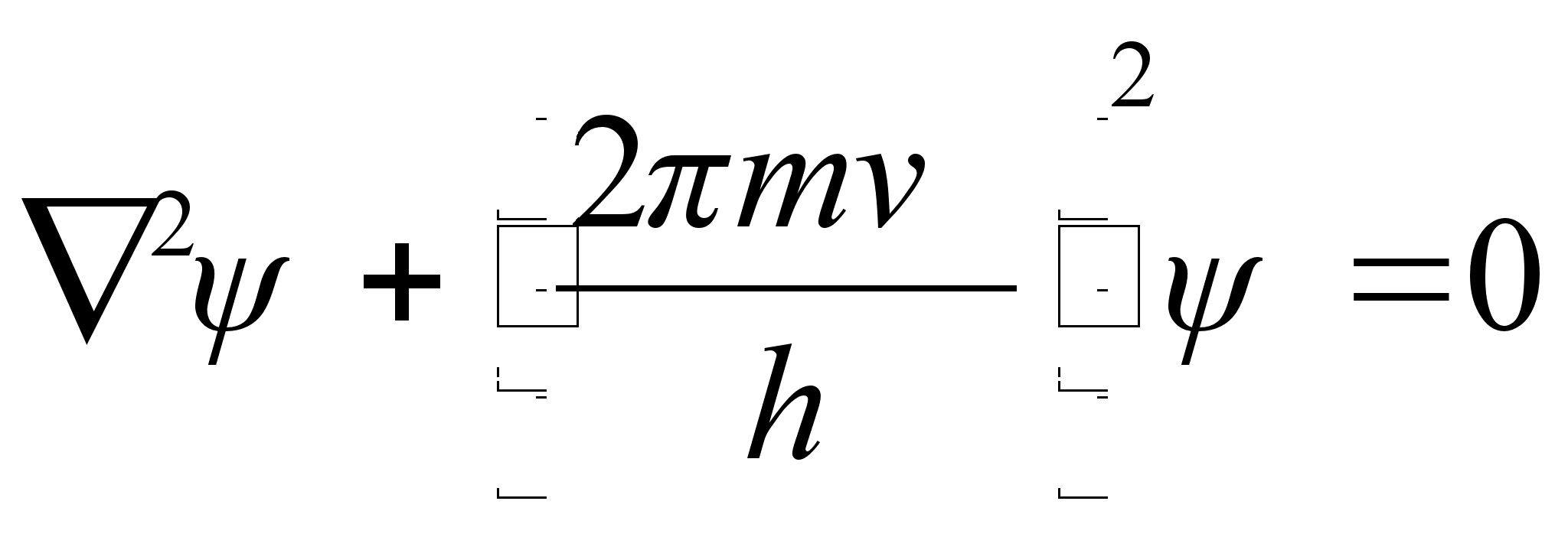
Et lainete oluliseks parameetriks on mitte kiirus, vaid energia, siis avaldame kiiruse kineetilise energiaga kui koguenergia ja potentsiaalse energia vahega:
![]()
ja
![]()
See on
kvantmehaanika põhivõrrand, nn. Schrödingeri
võrrand, ja tema kolmemõõtmeline lahend esitabki
lainefunktsiooni, mis kirjeldab elementaarosakest kui seisvat lainet
potentsiaaliaugus. Viimane tingimus tähendab, et lahend on
olemas kui koguenergia on negatiivne. Selle võrrandi ruumiline
(kolmemõõtmeline) lahend esitabki elementaarosakese kui
võnkumise. Lainetav osakene võib esinaeda teatud
tõenäosusega igas ruumipunktis. Osakese esinemise
tõenäosuse tihedust kirjeldab lainefünktsiooni ruut
![]() ja tema leidmise tõenäosus ruumiosas dV on
ja tema leidmise tõenäosus ruumiosas dV on ![]() .
Tuuma ümber tiirleva elektroni korral on koguenergia määratud
Bohri aatomi jaoks leitud tingimustega ja lainete arv mingil
energianivool on võrdne täisarvuga n, mis
iseloomustas seda energianivood.
.
Tuuma ümber tiirleva elektroni korral on koguenergia määratud
Bohri aatomi jaoks leitud tingimustega ja lainete arv mingil
energianivool on võrdne täisarvuga n, mis
iseloomustas seda energianivood.
Oluline on tähele panna, et Schrödingeri võrrand ei sisalda aega, seega elektroni leidmise tõenäosus mingis punktis on kogu aeg üks ja seesama, elektron asub kogu aeg mingis piiratud ruumiosas. Elektroni hoiab selles ruumiosas elektriväli, mille potentsiaal on negatiivne, st., mis tõmbab elektroni. Tõmbavat, madalama potentsiaaliga (elektroni potentsiaalse energiaga) ruumiosa nimetatakse ‘potntsiaaliauguks’, analoogia põhjal auguga maapinnas, kuhu sissekukkunud kehad sealt ise enam välja ei pääse. Tuumale lähenenud elektron ongi kukkunud potentsiaaliauku. Joonisel on näidatud lihtsaim ühemõõtmelise potentsiaaliaugu juht, kus väljaspool ‘auku’ on potentsiaal ühtlaselt kõrgem ja augus sees ühtlaselt madalam, tuletades meelde näiteks kaevu maapinnas. Elektroni lainetamist niisugune potentsiaaliaugus on matemaatiliselt lihtne arvutada, sest summaarne energia E-Ep on augus sees kõikjal sama ja võrrand (???) laheneb sinusoidaalsete võnkumistena. Tähtis on, et võrrand ei lahene mitte igasuguse energiaväärtuse puhul, vaid ainult niisuguste puhul, mis võimaldavad augu mõõtmesse paigutada täisarvu poollaineid. Sisuliselt tähendab see tingimus, et augu servas, kus potentsiaal järsult tõuseb, peab elektroni leidmise tõenäosus olema null (vt. joonist). Siit tulenebki potentsiaaliaugus asetseva lainetava elektroni lubatud energia kvantiseeritus, mille tulemusena võrrand laheneb ainult teatud täisarvuliste kordajatega n seotud energiaväärtuste jaoks. Kvantarvu n mõte on sama, mis Bohri aatomis, ta seob elektroni lubatud energia Plancki konstandi h kaudu võnkesagedusega, lainepikkusega, mis täpselt mahub ‘potentsiaaliauku’.
Kuigi elektroni leidmise tõenäosus mingis ruumipunktis on konstant, sõltub see oluliselt, millist ruumipunkti me vaatleme. Näiteks potentsiaaliaugu serval on see null ja on null iga poollaine järel. Poollaineid on seda rohkem, mida kõrgem on elektroni energia. Muide, täpselt null on elektroni leidmine seina-ääres ainult siis kui ‘sein’ on lõpmatu kõrge, st. potentsiaaliauk on väga sügav, väga madala pontentsiaaliga. Madalasse seina tungib elektron veidi sisse, ja kui see sein ei ole mitte väga paks, siis ulatub lektroni lainetus veidi ka naaberauku (Joonis tunnelefekti kohta). Seega, elektron, mis asub piiratud madala potentsiaaliga ruumiosas võib siiski teatud väikese tõenäosusega sattuda ka naaberauku, kuigi nende vahel on sein. Seda nähtust nimetatakse tunneleffektiks ja sellel on bioloogias suur tähtsus elektroni ülekandeprotsessides: Kui lähestikku asuvad kaks aatomit, siis võib elektron kanduda üle ühelt teisele, kuigi vahepeal on kõrge potentsiaaliga ruumiosa (‘sein’).
Nagu öeldud, on Schrödingeri võrrand lihtne lahendada ja annab siinusekujulised lained ainult siis kui summaarne energia on potentsiaaliaugus konstantne. Aatomituuma ümbruses aga on potentsiaaliauk hoopis sügava lehtri kujuline, langedes pöördvõrdeliselt kaugusega tuumast. See teebki võrrandi lahendamise keeruliseks ja annab tulemuseks mitte konstantse lainepikkusega siinuselised lained, vaid pidevalt lüheneva lainepikkusega lained, seda lühema lainepikkusega, mida madalam on potentsiaal antud kaugusel. Kirjutame need lahendid vesiniku aatomi jaoks siiski välja, sest nendest tulenevad kvantarvud, n, l, ja m, mis määravad elektronide võimaliku paigutuse aatomis.
Elektroni lainetus vesiniku aatomis
Schrödingeri võrrandi lahendamine ümber tuuma asetseva elektroni jaoks on eelmises punktis vaadeldust keerukam kahel põhjusel: esiteks, lahend ei ole mitte ühemõõtmeline, vaid kolmemõõtmeline ja potentsiaaliauk ei ole mitte sileda põhjaga, vaid lehtrikujuline. Kuna probleem on ilmselt tsentraalsümmeetriline, siis on otstarbekas Schrödingeri võrrand kirjutada ruumilistes polaarkoordinaatides r, ja Tuletame meelde, et rist-ja polaarkoordinaadid on omavahel seotud järgmiselt:
![]()
![]() ja
ja ![]()
Asendades need Scrödingeri kolmedimensionaalsesse võrrandisse saame matemaatiliselt järgmise üldvõrrandi elektroni kohta vesiniku aatomis
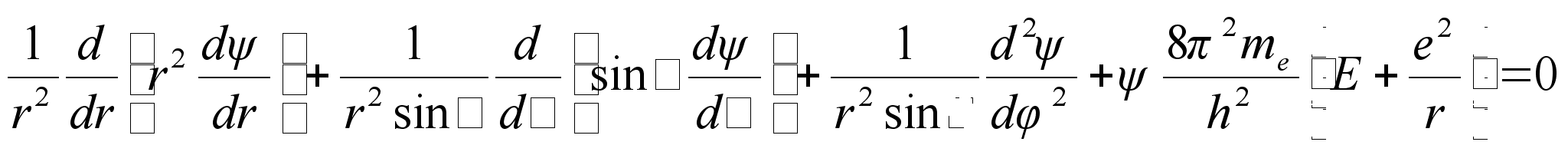
Siin me on elektroni mass. Selle võrrandi lahendamine üldjuhul ei olegi võimalik, vaid vaja on teha teatud eeldusi. Nimelt eeldatakse, et kolmemõõtmeline lainefunktsioon avaldub kolme ühemõõtmelise lainefünktsiooni korrutisena:
![]()
See on füüsikaliselt väga oluline koht, eeldades, et võnkumised kolmes eraldi ruumi suunas toimuvad sõltumatult, üksteist mõjutamata. Elektroni summaarne energia kujuneb välja kolmesuunaliste võnkumiste energiate summana. Rakendades seda eeldust ja tehes matemaatilised teisendused saame kolm eraldi võrrandit, igaüks oma koordinaadis toimuvate võnkumiste kohta:
![]()
![]()
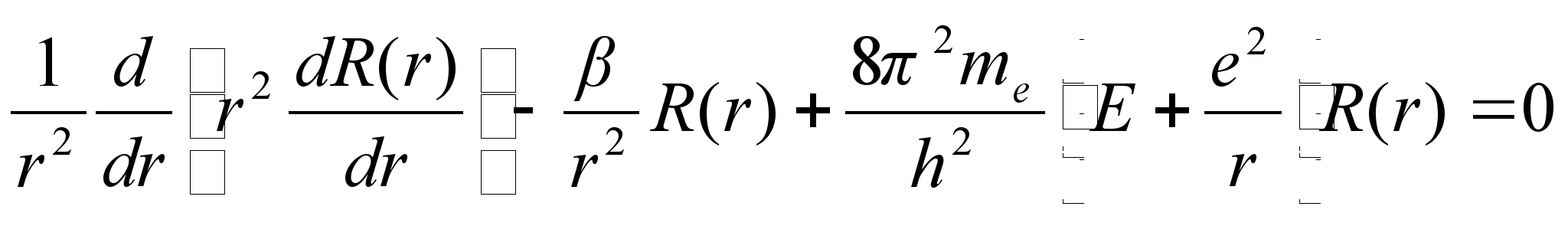
Nendes võrrandites m ei ole elektroni mass vaid mingi täisarv, samuti nagu
Esimene kolmest võrrandist lahendub väga lihtsalt. Nagu oodatud, on võnkumised polaarnurga suunas siinuselised, sest asimuudi suunas on ju potentsiaalne energia konstantne. Täisarv m on siin lubatud energiat määrava kvantarvu rollis.
![]()
Samuti annab siinuselise lahendi teine võrrand, sest ka polaarnurga suunas on potentsiaalne energia konstantne. Siin on aga lahend keerukam, sest sisldab kahte kvantarvu, m ja Keerukaim lahend on aga raadiusesuunaline, sest siin on potentsiaalne enegia muutlik, pöördvõrdeline raadiusega. Ometi onkasee lahendatud ja leitud tingimused kvantarvu n jaoks, mille puhul lahend on olemas (lubatud energiate väartused).
Ülatoodud võrrandites on kvantarvud esitatud siiski keerukamal kujul kui lihtsas Schrödingeri võrrandis. Põhjus on selles, et, nagu mainisime, on elektroni summaarne energia nüüd määratud kolme energia summaga, vastavalt igas koordinaadis toimuvale võnkumisele. Keemiliste ja füüsikaliste protsesside jaoks on aga tihti kõige tähtsam summaarne energia, pealegi võimaldaks ühe summaarset energiat väljendava kvantarvu sissetoomine siduda kolmemõõtmeliselt võnkuva elektroni ühemõõtmeliselt tiirleva elektroni kvantiseeritud energiaga, nii nagu see oli Bohri aatomis. Seega, tuleks tuua sisse peakvantarv n, mis näitab kõigis koordinaatides toimuvate võnkumiste energiate summat, ja kõrvalkvantarvud, mis näitavad, kui suur osa summaarsest energiast on jaotunud ühe või teise koordinaadi suunas. Niisuguset loogikast tulenebki, et võrrandid ja jaoks sisaldavad juba ise mingeid täisarve, mis on allutatud täisarvule n, mis ei sisaldu R võrrandis vaid tuleneb selle lahenduvuse tingimusena. See alluvuste jada on järgmine:
Täisarv n, peakvantarv, võib omada täisarvulisi positiivseid väärtusi alates nullist: n=0, 1, 2, 3, ...
Füüsikaliselt, n näitab võngete (lainete) koguarvu raadiuse r ja tõusunurga suunas kokku.
Valemis
??? ![]() kus l võib omada positiivseid täisarvulisi
väärtusi 0, 1, 2, 3, ...n-1. Suurust l nimetatakse
orbitaalkvantarvuks ja see näitab, mitu võnget on
tõusunurga suunas. Võnked asimuudi suunas
ei muuda elektroni energiat muidu kui aatom ei asetse välises
magnetväljas. Seetõttu ei olegi asimuudisuunalisi võnkeid
energiat määravate võngete koguarvu sisse loetud ja
kvantarvu m nimetatakse magnetkvantarvuks. Tema lubatud
väärtused on allutatud orbitaalkvantarvu l
väärtustele ja võivad olla vahemikus –l..0..+l.
kus l võib omada positiivseid täisarvulisi
väärtusi 0, 1, 2, 3, ...n-1. Suurust l nimetatakse
orbitaalkvantarvuks ja see näitab, mitu võnget on
tõusunurga suunas. Võnked asimuudi suunas
ei muuda elektroni energiat muidu kui aatom ei asetse välises
magnetväljas. Seetõttu ei olegi asimuudisuunalisi võnkeid
energiat määravate võngete koguarvu sisse loetud ja
kvantarvu m nimetatakse magnetkvantarvuks. Tema lubatud
väärtused on allutatud orbitaalkvantarvu l
väärtustele ja võivad olla vahemikus –l..0..+l.
Seega, seoses sellega, et ruum on kolmemõõtmeline, on elektronil kolm kvantarvu, mis iseloomustavad võngete arvu iga koordinaadi suunas. Selleks, et üks kvantarv iseloomustaks võimalikult hästi koguenergiat, on võrrandid lahendatud nii, et peakvantarv n vastab kahe koordinaadi raadiuse ja tõusunurga suunas toimuvate võngete koguarvule.Asimuudi suunas toimuvad võnked ei mõjuta elektroni koguenergiat muidu kui aatom ei asetse välises magnetväljas, seetõttu on magnetkvantarv m summast välja jäetud. Peame meeles järgmised reeglid:
n=1,2,3,4,5....
l=0, 1, 2 ...(n-1)
m=0, ±1, ±2, ...±l.
Peakvantarv n võib omada positiivseid täisarvulisi väärtusi.
Orbitaalkvantarv ehk kõrvalkvantarv l võib omada täisarvulisi väärtusi alates nullist kuni ühe võrra väiksema väärtuseni kui n. See tähendab, et tõusunurga suunas ei pruugi toimuda ühtegi võnget, võib toimuda üks, kaks jne, võnget, kuid vähemalt üks võnge peab jääma raadiuse suunale, muidu kaotaks aatom raadiusemõõtme, mis on ju ainuke pikkuse dimensiooniga suurus kolme polaarkoordinaadi hulgas.
Magnetkvantarv m on allutatud kõrvalkvantarvule ja võib omada väärtusi alates –l läbi nulli kuni +l –ni. Keemikud on mugavuse mõttes tähistanud kvantarvude väärtusi ka tähtedega:
Peakvantarvu jaoks: K(n=1); L(n=2); M(n=3); N(n=4) jne
kõrvalkvantarvu jaoks: s(l=0); p(l=1); d(l=2) f(l=3).
Joonisel on illustreeritud rariaalkomponendi R kuju sõltuvalt peakvantarvu n ja kõrvalkvantarvu l väartustest. Kui n=1 siis on elektronil ainult üks laine ja see peab olema raadiusesuunaline (l=0). Laine ei ole aga siinuseline, vaid muutub väga kõrgeks ja teravaks tuumale lähedases ruumiosas, seoses sellega, et seal potentsiaaliauk kukub kiiresti sügavaks. Kui n=2 ja l=0, on raadiusesuunas kaks lainet, kui n=3 ja l=0, on raadiusesuunas kolm lainet. Nüüd on eriti selgesti näha, kuidas potentsiaali langemine tuuma suunas põhjustab lainepikkuse pidevat lühenemist. Pange tähele ka, kui kaugele aatomi tsentrist elektroni lained ulatuvad: ühe võnke puhul umbes 4 A (A=Ongström, = 10-10 m= 0.1 nm), kahe võnke puhul 6A ja kolme puhul 12 A. See arv kahekordselt on vesinikuaatomi läbimõõt sõltuvalt sellest missugusel energianivool elektron asub (kas n=1,2 või 3). Seega, põhisesundis n=1 katab aatomi lainefunktsioon diameetri umbes 8A, kuid ergastatud seisundis (n=2 või 3) kuni 20 A. Kui l =1, on raadiuse suunas üks võnge vähem, kui l=2 siis kaks võnget vähem, kuid aatomi üldmõõt sellest ei muutu, vaid raadiusesuunaline lainepikkus vastavalt suureneb. (Kuidas see ühtib väitega, et muutujate lahutamine tähendab eeldust, et võnked kolmes koordinaadis on sõltumatud??).
Eelmises lõigus leidsime, et elektroni leidmise tõenäosuse tihedust esitab lainefunktsiooni ruut (lainefunktsioon võib olla ka negatiivne, kuid ruut on ikka positiivne). Tõenäosuse tihedus korrutatud vastava ruumi suurusega annab elektroni leidumise tõenäosuse selles ruumiosas. Juhul kui l=0 on lainefunktsioon maksimaalne kohal r=0, seega tuuma vahetus ümbruses on elektroni tõenäosustihedus suurim. Kuna aga tuum ise on tohutult pisike (ruum väheneb raadiuse kuubiga!) siis elektroni leidumise tõenäosus otse tuumas on ikkagi väga-väga väike, nagu näha ka vastavalt jooniselt. Sõltuvalt raadiusesuunaliste leinete arvust moodustab elektron tõenäosuspilve millel on üks, kaks, kolm või enam suurma tihedusega kohta, tuumast keskmiselt seda kaugemal, mida suusrem on n. See langeb kokku Bohri aatomi analüüsil saadud tulemusega, et elektron võib tiirelda kindlatel kaugustel, seda kaugemal, mida suurem on energia, kuid lainemehaanikast näeme, et elektroni orbiit ei ole mitte kindel joon vaid muutuva tihedusega tõenäosuse pilv.
Pilt läheb veelgi huvitavamaks kui katsume lainefunktsiooni kolme koordinaadi suunalisi komponente korraga ette kujutada, seega aatomi ruumilist pilti ette kujutada. Aatom on lihtne kerakujuline ainult juhul kui võnked on ainult raadiuse suunas (l=0 ehk s-orbitaalid). Kui l=1 (p-orbitaalid) on tõusunurga suunas ka võnge, mis moonutab kerakujulise tõenäosuspilve kaheksakujuliseks. See kaheksakujuline moodustis võib ruumis paikneda kolmel viisil, vastavalt m=-1,0+1, nii nagu näidatud joonisel. Kui välist magnetvälja ei ole, siis need erinevad paiknemisviisid koguenergiat ei mõjuta. Magnetvälja olemasolul aga mõjutavad ja vastavalt jagunevad spektrijooned kolmeks. Siit siis kolmanda kvantarvu nimetuski - magnetkvantarv. Kui l=2 ja tõusunurga suunas on kaks võnget, tekivad veelgi kummalisema kujuga moodustised viiel erineval moel. Seega, joonisel ?? toodud raadiusesuunalised tõenäosuspilved l väärtuste 1 ja 2 jaoks on kehtivad nendes ristlõigetes kus raadiusesuunaline tõenäosus on maksimaalne.
Milleks me bioloogilises füüsikas tungime nii sügavale kvantmehaanikasse? Selleks, et mõista, et ainult tänu aatomite lainelisele ehitusele on elu võimalik. Elusstruktuurid moodustuvad keerukast aatomite süsteemist, mis seostuvad üksteisega kindlates järjestustes ja kindlates suundades. Ruumiline struktuursus on ju valgu molekuli peamine omadus. Kui kõik valku moodustavad aatomid oleksid kujult ümargused nagu herneterad (näit. nagu Bohri aatomi ringikujulised orbiidid), siis ei oleks aatomite sidumine kindlates suundades võimalik. Ei ole ju herneteradest võimalik kokku panna keerulisi ehitisi, küll on see aga võimalik näiteks Logo elementidest, mis ei ole ümargused. Isegi lihtne vee molekul näeks siis hoopis teistsugne välja kui aatomid oleksid ümargused. Tänu sellele, et p ja d orbitaalid (l=1 ja 2) moodustavad ruumilis kujundeid millel on väljavenitused kindlates suundades, haakuvad nendega teiste aatomite p- ja d-elektronid moodustades kindlasuunalisi sidemeid. Niimoodi, üksteisest kindlatel kaugustel ja kindlates suundades paigutatud aatomitest ehituvad üles elusaine molekulid, nendest omakorda rakud ja koed ja organismid. Aatomite paigutus molekulis ja molekulide omavaheline haakumine määrabki selle kuidas elusaine üles ehitatakse. Seega, elu olemust saab mõista ainult mõistes kvantmehaanika põhialuseid.
Mitme elektroniga aatomid
Kuigi vesinik on üks tähtsamaid looduses esinevaid elemente, on bioloogias siiski tähtsad veel süsinik, lämmastik, hapnik ja veel mitmed teised elemendid. Süsinikul on kuus, lämmastikul seitse ja hapnikul kaheksa elektroni. Kvantmehaanilist lainevõrrandit saab aga täpselt lahendada ainult kahe keha jaoks, seega ühe elektroni ja ühe prootoni jaoks. Mitme elektroniga aatomites on oluline veel elektronide omavaheline mõju ja selle täpne arvestamine ei ole võimalik. Meie siin unustame elektronide vastatstikuse mõju ja kujutame ette, missugune oleks mitme elektroniga aatom kui elektronid omavahel üksteist ei mõjutaks vaid kõik oleksid vastasmõjus ainult tuumaga.
Kui elektrone on mitu, on ka prootoneid mitu ja vastavalt on tuuma laeng suurem ja elektriline külgetõmme tugevam. Seega on tuuma ümbruses ‘potensiaaliauk’ sügavam (potentsiaalne energia langeb kiiremini) ja põhisesundi n=1 lainefunktsioon koondub tuumale lähemale. Samuti on tuumale lähemal ka teised, kõrgemale energiale vastavad orbitaalid. Kuidas aga paigutuvad elektronid, kas kõik ühel, kõige madalama energiaga orbitaalil? Ei, selgub, et täpselt ühesuguse lainefunktsiooniga elektrone saab aatomis olla ainult üks. See on nn. Pauli printsiip, mille kohaselt elektronid jaotuved erinevate energianivoode vahel täites need madalamast kõrgemani. Seega peaks igale orbitaalile mahtuma ainult üks elektron, mis on iseloomustatud kolme kvantarvuga n, l, m. Selgub aga, et elektronil on veel üks omadus, mis lisab veel ühe kvantarvu, spinn s, mis kirjeldab elektroni sisemine pöörlemise suunda. Kuigi on raske ette kujutada kuidas üks tõenäosuspilv veel sisemiselt iseenese ümber pöörleb nagu värten (inglise keeles “spin”) ilmneb see sellest, et elektronil on magnetmoment. Iga elektron on nagu pisike magnetike, mis võib olla suunatud tuuma magnetvälja suhtes (ka tuumal on magnetmoment) kahes erinevas suunas. Vastavatest võrranditest tuleneb selle kvantarvu väärtuseks kas +1/2 või –1/2. Ühele ja samale orbitaalile mahub seega kaks elektroni, üks spinniga =1/2 ja teine spinniga –1/2. Nüüd on meil käes kõik tingimused, et asuda üles ehitama paljuelektroniliste aatomite elektronkatte struktuuri: elektrone tuleb juurde lisada orbitaalidele järjekorras, alates madalamate energiatega seisunditest kõrgemate suunas, mahutades igale orbitaalile mitte rohkem kui kaks elektroni. Teeme selle programmi läbi kuni teise perioodi (n=2) kõigi nivoode täitumiseni, sest see kaasab ka bioloogiliselt tähtsad elemendid C, N, O.
H: n=1;l=0;m=0;s=1/2 üks paardumata spinniga elektron, keemiliselt aktiivne
He: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2 kõik elektronid paardunud spinnidega, inertgaas
Li: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2
n=2;l=0;m=0;s=1/2 üks paardumata spinniga elektron, keemiliselt aktiivne
Be: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2
n=2;l=0;m=0;s=1/2
n=2;l=0;m=0;s=-1/2 kõik elektronid paardunud spinnidega, keemiliselt inertne
B: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2
n=2;l=0;m=0;s=1/2
n=2;l=0;m=0;s=-1/2
n=2;l=1;m=-1;s=1/2 üks paardumata spinniga elektron, keemiliselt aktiivne
C: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2
n=2;l=0;m=0;s=1/2
n=2;l=0;m=0;s=-1/2
n=2;l=1;m=-1;s=1/2
n=2;l=1;m=0;s=1/2 kaks paardumata spinniga elektroni, keemiliselt aktiivne
N: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2
n=2;l=0;m=0;s=1/2
n=2;l=0;m=0;s=-1/2
n=2;l=1;m=-1;s=1/2
n=2;l=1;m=0;s=1/2
n=2;l=1;m=1;s=1/2 kolm paardumata spinniga elektroni, keemiliselt aktiivne
O: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2
n=2;l=0;m=0;s=1/2
n=2;l=0;m=0;s=-1/2
n=2;l=1;m=-1;s=1/2
n=2;l=1;m=-1;s=-1/2
n=2;l=1;m=0;s=1/2
n=2;l=1;m=1;s=1/2 kaks paardumata spinniga elektroni, keemiliselt aktiivne
F: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2
n=2;l=0;m=0;s=1/2
n=2;l=0;m=0;s=-1/2
n=2;l=1;m=-1;s=1/2
n=2;l=1;m=-1;s=-1/2
n=2;l=1;m=0;s=1/2
n=2;l=1;m=0;s=-1/2
n=2;l=1;m=1;s=1/2 üks paardumata spinniga elektron, keemiliselt aktiivne
Ne: n=1;l=0;m=0;s=1/2
n=1;l=0;m=0;s=-1/2
n=2;l=0;m=0;s=1/2
n=2;l=0;m=0;s=-1/2
n=2;l=1;m=-1;s=1/2
n=2;l=1;m=-1;s=-1/2
n=2;l=1;m=0;s=1/2
n=2;l=1;m=0;s=-1/2
n=2;l=1;m=1;s=1/2
n=2;l=1;m=1;s=-1/2 kõik elektronid paardunud spinnidega, inertgaas
Ülaltoodud orbitaalide täitumise järjekorrast näeme, et kõigepealt täituvad orbitaalid ühe elektroniga ja alles nende võimaluste ammendumisel asub teine, vastupidise spinniga elektron samale orbitaalile.
Illustratsiooniks toome täieliku perioodilise süsteemi tabeli, mis näitab orbitaalide täitumise järjekorda ka kõrgema n väärtuse jaoks kui n=2. Põhimõte on see, et s-orbitaalidele (l=0) mahub kaks elektroni 2x(m=0); p-orbitaalidele (l=1) mahub kuus elektroni 2x(m=-1,0+1); d-orbitaalidele (l=2) mahub kümme elektroni (m=-2,-1,0,1,2). Aga juba alates komanda perioodi lõpust tekivad ebaregulaarsused, mis on põhjustatud sellest, et võnked tõusunurga suunas on mõnevõrra energiarikkamad kui võnked raadiuse suunas. Seetõttu pärast Argooni (Ar) oleks oodata elektronide asumist 3d nivoole, kuid K ja Ca aatomites täituvad enne hoopiski 4s orbitaalid, mis asuvad energeetiliselt madalamal kui 3d orbitaalid. Alles seejärel täituvad järjekorras 3d orbitaalid, jättes 4s orbitaalile kogu aeg 2 (või üks ) elektroni. Seetõttu omab terve rida aineid Sc kuni Zn –ni keemiliselt sarnaseid metallilisi omadusi ja terve see rida kannab ühist nimetust muldmetallid. Samasugused ebaregulaarsused korduvad veelgi enam kõrgemate n väärtuste puhul. Bioloogias on olulised elemendid Fe, Cu, Mn, mis võivad kergesti loovutada ühe või kaks väliskihi (n=4) elektroni, kuigi eelmises, 3d kihis on veel vabu orbitaale. Neid viimaseid, vabu 3d orbitaale, on loodus osanud kasutada nende aatomite sidumiseks valkudega, et neid paigutada kindlatele kohtadele ja seal fikseerida, samal ajal kui n=4 kihi elektrone saab aatom loovutada või juurde võtta. Seetõttu on nimetatud metallid kõige tüüpilisemad elektroni ülekandjad, olles kinnistatud nn. tsütokroomidesse (Fe) või teistesse valkstruktuuridesse (Cu, Mn).
Huvitaval kombel on plaatina ja kulla (Pt, Au) väliskihi struktuur sarnane kaaliumi (K) omaga. Viimane on aga keemiliselt väga aktiivne, samal ajal kui kuld võib kolmsada aastat merevees püsida tuhmumata.
Molekulide moodustumine – kovalentne side aatomite vahel.
Orbitaalil üksi asuv elektron omab magnetmomenti ja püüab paarduda teise, vastassunalise spinniga elektroniga, nii nagu kaks pulkmagnetit tõmbuvad kui põhja- ja lõunapoolused satuvad vastatstikku. Seetõttu on keemiliste elementide aatomid ja ka molekulid, mille koosseisus on paardumata elektrone, keemiliselt aktiivsed ja neid nimetatakse radikaalideks. Kui lähedal juhtub olma teine aatom, millel vaba elektron on vastasmärgilise spinniga, võiksid need kaks elektroni põhimõtteliselt paari moodustada, kuid selleks peavad nad enne teineteisele küllat ligidale saama. Probleem on selles, et dipoolsed magnetid (kahepooluselised) magnetid tõmbuvad piisavalt tugevasti ainult väikeselt kauguselt, välised elektronid aga tõukuvad omavahel juba suurelt kauguselt. Seetõttu molekuli moodustumiseks peavad elektronkatted alguses lähenedes isegi teatud määral tõukejõudude poolt moonutatud saama, enne kui tõmbuvad jõud piisava tugevuse saavutavad. Molekuli moodustumine on kvantmehaaniliselt väga keerukas protsess ja vastavaid lainevõrrandeid täpselt lahendada ei ole niikuinii võimalik. Näiteks on niisuguses kahe paardunud elektroni lainefunktsioonis elektroni maksimaalne tõenäosustihedus otse tuumade vahel. Seega, lisaks spinnide kui magnetite vastastikusele tõmbele on oluline veel mõlema tuuma tõmme nende vahel asuva elektroni suhtes. Meie kursuse piires on piisav mõista, et keemilise sideme kahe aatomi vahel saavad moodustada ainult kaks paardumata elektroni, millel on vastassuunalised spinnid, ja paardunud elektronidest tingitud tugev aatomitevaheline tõmme on mõjus ainult väikestel kaugustel.
Vaatleme molekuli moodustumist energeetilisest aspektist. Kui kaks aatomit asuvad kaugel, võib nende omavahelise mõju potentsiaalse energia lugeda nulliks (mõju ei ole). Lähenedes hakkab tunda andma kõigepealt väliste elektronide omavaheline tõukumine. Seda tõukejõudu ületades potentsiaalne energia suureneb, muutudes positiivseks. Potentsiaalse energia suurnemine toimub loomulikult kineetilise energia vähenemise arvel, s.t. molekulid lähenevad inersi tõttu ja lähenedes kiirus aeglustub. Kui algkiirus oli küllalt suur võivad elektronid üksteisele nii lähedale sattuda (potentsiaalne energia saavutab maksimumi), et antiparalleelsete spinnidega elektronide tõmme hakkab domineerima Seevastu elektronpilvede tõukumine isegi väheneb, sest elektronid asuvad nagu üksteise sees, orbitaalid osaliselt kattuvad. Tõmbejõu sfääris hakkab potentsiaalne energia uuesti kahanema, kineetiline seevastu aga suurenema. Tuumade teatud omavahelise kauguse puhul saabub potentsiaalse energia miinimum, aga muidugi uuesti kineetilise energia maksimum. Kui selles seisus aatomipaar energiat ära ei anna, siis stabiilset molekuli ei moodustu. Põrgates naabermolekuliga või energiakvanti kiirates saab ülearusest energiat vabaneda ja siis stabiliseerub potentsiaalse energia miinimumi seisund. Pange tähele, et vabanenud energia muutub just kogu molekuli energiaks, mitte uuesti nendesamade aatomite kineetiliseks energiaks, mis reaktsiooni astusid. Reageerivad aatomid on oma kineetilise energia abil ületanud nn. aktivatsioonienergia barjääri ja moodustanud stabiilse molekuli, vabanedes seejuures ülearusest energiast. Uus energiamiinimum, mis vastab molekuli olekule, võib olla kas madalam või kõrgem kui aatomite esialgne potentsiaalse energia nivoo (null). Kui lõppnivoo on madalamal kui algnivoo, siis selles reaktsioonis vabanes energiat (ka see muutus molekulide liikumise energiaks, soojuseks). Kui lõppnivoo on kõrgem kui algnivoo, siis reaktsioonis kokkuvõttes neeldus kineetilist energiat, s.t. osa aatomite kineetilisest energiast ei muutunud mitte molekulide kineetiliseks energiaks, vaid jäi molekulisiseseks potentsiaalseks energiaks. Niisuguse reaktsiooni tulemusena segu jahtub, molekulide kineetiline energia väheneb.
Ülaltoodud mudel ei kehti mitte üksne molekuli moodudstumise puhul aatomitest vaid ka teiste keemiliste reaktsioonide puhul, mis toimuvad molekulide vahel ja mille tulemusena moodustuvad teised molekulid. Molekulide moodustumise puhul aatomitest on molekuli potentsiaalne energia tavaliselt negatiivsem kui reageerivate aatomite oma (energiat vabaneb). Molekulidevaheliste reaktsioonide puhul esineb nii negatiivsemat kui positiivsemat lõppseisundit.
Paarduda ja kovalentseid sidemeid moodustada võivad omavahel nii erinevate aatomite s-p ja d-elektronid kui ka s, p, ja d elektronid kombinatsioonides. Vastavalt paarduvate elektronide orbitaali kujule võivad sidemed kujuneda erineva pikkusega ja erinevate nurkade all. Lihtsaim juht, kui paarduvad kaks s-elektroni, annab tulemusena hantlikujulise molekuli, kus kaks kerakujulist orbitaali on osaliselt ühinenud (Joonis). s-elektronide paardumisel moodustun nn. -side, millel ei ole kindlat suunda. p-elektronidel on kaheksakujulised orbitaalid ja need võivad s-elektroniga paarduda otstest. Sel juhul on -side kaheksakujulise p-orbitaali otsa pikenduseks, suund on määratud p-orbitaali poolt. p-orbitaalid võivad omavahel paarduda kahel viisil, kas ka otstest (sel juhul on sideme nimetuseks ikkagi -side), või külgedelt. Viimasel juhul kutsutakse sidet -sidemeks. -sideme oluline omadus on see, et ta ei lase sidet moodustavaid aatomeid omavahel pöörelda, kuna side seda lubab. -sideme näiteks s- ja p-orbitaali vahel toome vee molekuli, kus s-orbitaaliga vesiniku elektron on paardunud p-orbitaaliga hapniku elektroniga (joonis). -sidemete näiteks toome lämmastiku molekuli, milles N aatomites on kolm omavahel risti olevat paardumata p-orbitaali. Üks neist paardub teise N aatomi p-elektroniga -sideme abil, kuna kaks paarduvad -sidemete kaudu, moodustades nii kolmekordse sidemega seotud (väga stabiilse, raskesti lõhutava) molekuli.
Võimalike kovalents-sidemete arv aatomis (aatomi võimalik valents).
Aatomite põhiseisundis (madalaimal energiatasemel) on nende kovalents võrdne paardumata elektronide arvuga, mis oleks
H: 1
He: 0
Li: 1
Be: 0
B: 1
C: 2
N: 3
O: 2
F: 1
Ne: 0
Tegelikult aga ei ole valentssidemete arv alati niisugune ja võib olla isegi muutlik sõltuvalt ühenditest. See tuleneb asjaolust, et 2s elektronpaar ei ole mitte väga tugevasti omavahel seotud ja termiline energia on juba võimeline seda sidet lõhkuma, viies ühe 2s elektronidest üle 2p seisundisse. Selle tulemusena on näiteks Be ja ka Ca tavaliselt kahevalentsed, kuigi mõlemad sisaldavad põhiseisundis 2s paari ja mitte ühtegi p-elektroni. Sama lugu on süsinikuga: see peaks teoretiliselt olema kahevalentne (2s paar ja kaks paardumata 2p elektroni), kuid on peaaegu kõigis ühendites, seljuures kõigis orgaanilistes hendites neljavalentne. Üks 2s elektronidest ergastub kolmandale vabale 2p orbitaalile ja kõik neli teise nivoo elektroni osutuvad mittepaardunuiks. Kui niisugusest ergastusseisundist kiiresti moodustuvad valentssidemed, nii et lisandunud tekkinud sidemetest vabaneb rohkem energiat kui kulus ergastusele, siis on niisugune vahepealse ergastuse kaudu moodustunud neljavalentne lõppseisund energeetiliselt madalalmal tasemel kui ergastumata seisundist moodustunud kahevalentne lõppseisund. Kuna valentssidemete moodustumisel vabanenud energia võib olla mitmesugune sõltuvalt moodustunus ühenditest, siis ei ole ka aatomi valents mingi kindel suurus. Küll aga on kindlam suurus maksimaalne võimalik valents, mis on määratud antud peakvantarvule n vastavate s ja p-nivoode üldhulgaga, eeldades, et teatud ergastusseisundites võivad need kõik olla asustatud paardumata elektroniga. Niisiis oleks teise perioodi elementide maksimaalne valents 4 (1 s ja 3p orbitaali) ja kolmanda perioodi elementidel 6 (1 s ja 5 p-orbitaali). Kahjuks tekib ka siin erandeid juhtudel kus kõrgema n väärusega s-orbitaalid on energeetiliselt madalamad kui uhe võrra madalama n-ga d orbitaalid.
Doonor-aktseptorside. Valents-sideme polariseeritus. Vesinikside.
Siiani oleme eeldanud, et kovalents-sideme moodustavad paardudes elektronid, millest üks kuulub ühele ja teine teisele aatomile. Kvantmehaanika lainevõrrandid aga ei tunnusta elektroni ‘kuuluvust’ vaid ainult tema kvantarve (energiaseisundeid). Seetõttu on peaaegu samaväärselt tõenäone juht, kus ühe aatomi elektronpaar moodustab sideme kasutades teise aatomi tühja orbitaali. Tähtis on ainult, et kuuludes kahele aatomile korraga omaks see paar madalamat energiat kui kuuludes ainult ühele aatomile. Niimoodi moodustuvad nn. koordinatsioonilised -sidemed, mis kasutavad näiteks Fe aatomi vabu d-orbitaale, et fikseerida seda aatomit erilises valkstruktuuris, nn. tsütokroomis, kus ta osaleb elektroni ülekandjana. Tsütokroomidel on bioenergeetikas esmajärguline roll.
Kui elektronpaar on moodustanud valents-sideme ja kuulub seega kahele aatomile korraga, siis see ei tähenda sugugi, et elektronid kuuluvad kummalegi aatomile võrdselt. Aatomitel on omadus tõmmata kogu paari suuremal või vähemal määral omaenda orbitaalile, jättes naabri orbitaali vastavalt tühjemaks. Selle tulemusena omandab eltronpaari tõmbav aatom negatiivsema kogulaengu kui tema partner ja seda omadust iseloomustatakse aatomi elektronegatiivsusena. Hapnik on üks elektronegatiivsemaid elemente (Tabel), seega ühendites tõmbab ta elektronpaari tugevasti enesele, jättes partneri orbiidi osa aega tühjaks. Niimoodi kovalentne side polariseerub. Polariseerumise äärmuslikuks väljenduseks on nn. ioonside, kus üks aatom on elektroni täielikult teisele üle andnud. Tüüpilised ioonsidemega seotud ühendid on leelismetallide soolad, nagu NaCl, kus Na on kaotanud elektroni ja muutunud positiivseks iooiks, Cl aga liitnud elektroni ja muutunud negatiivseks iooniks.
Kovalents-sideme polariseerituse ja doonor-aktseptor-sideme kombinatsioon on bioloogias ülitähtis vesinikside. Vesinikside moodustub positiivse osalaenguga aatomi vabaksjäänud orbitaali ja mingi teise aatomi olemasoleva elektronpaari kaudu. Näiteks vees on positiivse osalaenguga aatomiks vesinik, millelt hapnik on elektroni osaliselt ära tõmmanud, ja millel seetõttu 1s orbitaal on osa aega elektroniga asustamata. Mingi vee molekuli hapnikuaatomi 2s või 2p elektronpaar võib moodustada doonor-aktseptorsideme teise vee molekuli vesiniku osaliselt vaba orbitaali kasutades ajal mil see on vaba. Niimoodi saavad tekkida kovalentse iseloomuga sidemed erinevate vee molekulide vahel, mis neid seovad. Tulemusena on vesi vedelas olekus looduslikel temperatuuridel samal ajal kui tema analoog H2S on gaasiline. Vee juurde pöördume tagasi vedelike vaatlemisel. Teiste vesiniksidemete näidetena bioloogias on valgu sekundaarstruktuuri kujundavad vesiniksidemed ja DNA kaksikspiraali kujundavad vesiniksidemed.
Orbitaalide hübridisatsioon
Nagu öeldud, on süsinik tüüpiliselt neljavalentne, sest üks tema 2s elektronidest ergastub 2p nivoole ja tekib neli paardumata elektroni, kolm 2p nivool ja üks 2s nivool. Nende orbitaalid peaksid olema erineva kujuga, mistõttu ka koos süsinikuga tekkinud molekulid ei tohiks olla sümmeetrilised. Vaadeldes aga tüüpilist süsinikühendit metaani (CH4) on leitud, et kõik neli H aatomit on täiesti identse energiaga seotud ja paigutatud sümmeetriliselt tetraeedri (ruumilise nelitahuka) tippudesse. Seega peavad kõik neli orbitaali olema täiesti sarnase kujuga. See on fakt, mis otse ei tulene kvantmehaanilisest teooriast ja millele tuli otsida seletust, püüdes leida loogilisi võimalusi erinevate orbitaalide kombineerumiseks. Leitigi võimalus, et uued sümmeetrilised orbitaalid on kõik sarnased kombinatsioonid nelja erineva orbitaali lainefunktsioonidest, erinevused on ainult selles, missugused p-orbitaali funktsioonid liidetakse ja missugune lahutatakse (s-orbitaal on summas alati positiivselt). Sisuliselt tähendab see, nagu erinevate orbitaalide lainetused liituksid ja lahutuksid erinevates kombinatsioonides, kuid igas kombinatsioonis esinevad kõigi nelja orbitaali lainefunktsioonid. Niisugune orbitaalide hübridisatsiooninähtus on üsna sagedane ja isegi vee molekulis ei ole hapniku 2p orbitaalidega moodustunud s-sidemete vaheline nurk mitte 90° vaid 104.5°. See näitab, et hapniku kaks vesinikuga paardunud orbitaali ja kaks hapniku enese paari (2s ja 2p paarid) hübridiseeruvad kõik võrdseteks sarnase kujuga orbitaalideks mis suunduvad tsentrist tetraheedri nurkadesse, sarnaselt nagu metaani molekulis, kuid kahel puudub partner H-aatom. Selle tulemusena on doonor-aktseptor iseloomuga vesiniksidet võimelised moodustama kas elektronpaari, nii 2s kui 2p paarid. Nendest näidetest on näha, kuidas tekkiva ühendi sümmeetrilisus võimaldab saavutada ühendmolekuli kõige madalamat energiaseisundit, hoolimata sellest, et hapniku enese (samuti kui süsiniku) elektronstruktuur ei ole minimaalse energia seisundis. Teisest küljest tähendab see ka seda, et individuaalsete aatomite kvantmehaanilisi orbitaalide kujusid ei saa võtta aluseks keerukamate ühendite stereo-struktuuri arvutamisel, vaid määravaks jäävad keerulise molekuli struktuurist tulenevad energiaseisundid, mis on minimaalsed tavaliselt maksimaalse sümmeetriaga olekutes.
Resonants
Resonantsi olemuse selgitamiseks vaatleme lihtsat struktuuri, nitraatiooni NO3-(joonis). Selles esineb lämmastik neljavalentsena, olles saatnud ühe oma 2s elektronidest praktiliselt täielikult hapnikule ja vabastades nii maksimaalse koguse valents-sidemeid. Kuigi niimoodi tekkinud struktuur peaks olema ebasümmeetriline, on katsed näidanud, et kõikide O-aatomite seoseenergiad on võrdsed. See on võimalik kui kaksik- ja üksiksidemed on pidevas vaheldumises, nii et kaksiksidet ei saa lugeda kuuluvaks kindlale O-aatomile. Sarnane näide on ka bensooli molekul, kus niisugune kaksik- ja üksiksidemete vahelduvus katab pikema ringi, sidudes tervelt kuus C aatomit. Kvantmehaanilises käsitluses tähendab resonants-ringi või ka lineaarse resonants-ahela lainefunktsioon, sarnaselt hübridisatsiooniga, lineaarkombinatsiooni kõikidest osalevatest lainefunktsioonidest. Seejuures on resoneeruvad sidemed tunduvalt tugevamad kui ilma resonantsita. Samuti võib resoneeruva lainefunktsiooni ruumiline ulatus olla tunduvalt pikem kui ühel aatomil. Vastavalt pikeneb ka neelatava (kiirtava) elektromagnetilise kiirguse lainepikkus. Seetõttu on loodus kasutanud resoneeruvaid struktuure nähtavat valgust neelavate pigmendimolekulide ehitamiseks. Fotosünteesis kasutatavate pigmentide, klorofülli ka karotenoidide molekulides on kas ringstruktuuriga või lineaarsed reonants-ahelad ja need ained omavad neeldumisribasid nähtava valguse piirkonnas, samal ajal kui tavalised valgud, aminohapped ja enamik teisi bioloogilisi molekule neelavad ultravioletses piirkonnas.
Üleminekumetallide kompleksid
Üleminekumetallideks nimetatakse esimese suure perioodi (n=3) metalliliste omadustega aineid, millel järgmise perioodi (n=4) 4s nivool asub üks või kaks elektroni, kuid samal ajal on vabu orbitaale veel 3d nivool (Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu). Neist bioloogias omavad elektroni edastajatena suurt tähtsust Mn, Fe, ja Cu. Bioloogilistes struktuurides on oluline, et aktiivsed aatomid, mis tegelikult osalevad metaboolsetes protsessides, oleksid kinnstatud ja asuksid vajalikul kaugusel ja vajalikus asendis oma metaboolsete partnerite suhtes, millega neil tuleb suhelda näiteks elektrone vastu võttes ja edasi andes või mõnel muul moel. Valkstruktuurid täidavadki seda ülesannet, et kinnistavad metaboolselt aktiivsed aatomid vajalikesse asukohtadesse. Loomulikult ei saa valkudega seotus välistada aatomite termilist võnkumist ümber keskasendi, kuid välistab pöörlemise ja kindlasti translatoorse liikumise. Aatomite kinnistamiseks saab kasutada kovalentseid sidemeid, mida peab aga olema piisaval hulgal, et takistada liikumist kõikides suundades, jättes samal ajal mõned valentsid vabaks ka metaboolse aktiivsuse tarbeks. Nendele tingimustele vastavadki kolmanda perioodi üleminekumetallid, millel on piisavalt täidetud või täitmata d-orbitaale (kokku viis), et aatomit kinnistada. Seejuures sidemete sümmeetria kindlustatakse s, p ja d-orbitaalide hübridisatsiooniga. Tabelis toome mõned andmed bioloogiliselt oluliste aatomite jaoks.
Elektronkonfiguratsioon Mn Fe Cu
M 3d54s2 3d64s2 3d104s1
M2+ 3d5 3d6 3d9
M3+ 3d4 3d5 -
Ionisatsioonipotentsiaal (eV)
esimene 7.43 7.87 7.72
teine 15.64 16.18 20.29
kolmas 33.69 30.64 37.08
Iooni raadiused (A)
M 1.17 1.16 1.17
M2+ 0.80 0.77 0.72
M3+ 0.66 0.63 -
Orbitaalide hübridisatsioon ja aatomi geomeetriline struktuur
Hübridisatsioon Aatomi kuju Sidemetevaheline nurk
sp Lineaarne 180°
sp2 Tasapind, kolmnurk 120°
sp3 Tetraeeder 109°28’
dsp2 Tasapind, ruut 90°
dsp3 Trigonaalne kaksikpüramiid 90°
120°
d2sp3 Oktaeeder 90°
Rauaaatomi kasutamise näiteks bioloogias on heemid, kus Fe aatom (klorofüllis aga raua asemel Mg) asetseb tasapinnalise porfüriiniringi keskel, olles kinnitatud koordinatsioonisidemetega. Heemid moodustavad aktiivosa sellistes valksüsteemides nagu hemoglobiin, müoglobiin, tsütokroomid ja mõndes fermentides, nagu katalaas, peroksüdaas. nII nagu aromaatilistes molekulides (näit. bensool) tavaliselt, on ka porfüriiniringis pikk resonants-ahel, mille tulemusena elektronid on ‘delokaliseeritud’ ja nende lainefunktsioonid haaravad tervet ringi. Ringis osalev N aatom, sõltuvalt asukohast, on ise ringi seotud kas kahevõi kolme sidemega ja moodustab sideme rauaga vastavalt kas ühe paardumata elektroni või oma 2s elektronpaari abil, doneerides selle raua vabale 3d orbitaalile. Nii fikseeritakse N aatom neljast nurgast nelja ligandiga. Viiendaks ligandiks ristisuunas on tihti aminohappe histidiini üks N aatomitest mis doneerib oma elektronpaari teisele Fe 3d orbitaalile. Niisiis on Fe aatom fikseeritud jättes selle 4s2 elektronid vabaks bioloogilistereaktsioonide tarbeks. Tavaliselt on need elektronid lahkunud ja aatom asub F2+ seisundis. Hemoglobiinis, mille molekulmass on 65000, on neli subühikut nelja heemiga. Müoglobiinis on üksainus subühik ühe heemiga. Hemoglobiinis on kuuendaks ligandiks kas hapnik või vesi, sõltuvalt kas hemoglobiin on hapnikuga rikastatud või mitte. Ka siin moodustub side sel teel, et hapnik doneerib oma elektronpaari Fe orbiidile, jättes O2 molekuli (või H2O molekuli) terveks. Vee ja O2 kõrval on seostumisaktiivsed veel CO ja NO, kusjuures CO seostub müoglobiinile umbes 50 korda ja hemoglobiinile isegi 200 korda tugevamalt kui O2.
Tsütokroomides on Fe viis ligandi samad kui hemo- ja müoglobiinis, kuid kuna tsütokroomid ei kanna molekule, vaid ainult elektrone, siis on ka kuues suund seotud bioloogiliselt passiivse ligandiga, kasutades selleks tavaliselt aminohappe metioniini S aatomi elektronpaari. Elektronide vahetus toimub F2+/F3+ seisundite vaheldumise teel.
Peptiidside
Valkude struktuur on suuresti mäaratud peptiidsideme omadustega, mis seob aminohapped pikaks ahelaks, polüpeptiidiks. Side moodustub ühe aminohappe karboksüülrühma –COOH ja teise aminohappe aminorühma –NH2 vahel, vee eraldumise teel, andes tulemuseks -CO-NH- sideme. Struktuurselt näeb side välja järgmine:
Röntgenstruktuuranaüüs aga näitas, et C-N side, mille tavaline pikkus on 0.147 nm, on peptiidsidemes lühem, 0.132 nm. See tähendab, et ühekordse sideme asemel moodustub tegelikult kahekordne side, vähemalt osaliselt. Seletus on siin järgmine. Tänu oma elektronegatiivsusele tõmbab O aatom kogu struktuuri elektronpilve eneda suunas järjekorras N->C->O. Selle tulemusena O paardumata elektron saab endale paarilise ja üks kovalentsetest sidemetest O-C vahel osaliselt katkeb. Selle asemel aga N jääb ühest elektronist osaliselt ilma ja tema elektronpaar püüab uut paarilist leida. See on saadaval C aatomis, mis kaotas sideme O-ga ja loob uue sideme N-ga. See uus side aga vaheldub pidevalt vanaga, nii et tegelikult on O=C=N süsteem seotud nagu pooleteise sidemega pidevalt. Seejuures kõik kolm aatomit hübridiseeruvad ühesugusteks sp hübriidideks. Orbitaalid O(sp2) ja C(sp2), samuti nagu C(sp2) ja N(sp2) kattuvad pikisuunas, moodustades -sidemed. Kolm p-orbitaali N, C ja O aatomites kattuvad külgsuunas -sidemetega risti ja moodustavad delokaliseeritud -elektronide süsteemi. -sidemed keelavad C-N aatomite vahelisel sidemel pöörlemise. Joonis näitab, kuidas lõpptulemusena O-C-N-H aatomid paigutuvad ühte tasapinda, jäigalt fikseerides nende omavahelise asendi. Pange tähele, et O ja H aatomid asuvad ahela vastaskülgedel (nn. trans-konfiguratsioon), mis valgu sekundaarstruktuuri moodustumiseks on oluline. Niisugused fikseeritud sidemed moodustavad ühe kolmandiku kogu peptiidahela sidemetest. Pöörlemisvõimalus jääb alles kahel kolmandikul ülejäanud sidemetest, aminohapete sisemistel C-N ja C-C sidemetel. Niisugune piiratus jätab oma jälje valgu sekundaarstruktuurile. Kui ülejäänud sidemed pöörduvad, tekib peagi olukord, kus iga mingi aminohappe O-aatom satub piisavalt ligistikku järjekorras kolmanda aminohappe H-aatomiga, et nende vahel moodustuks vesinikside (tänu ülalmainitud trans-konfiguratsioonile). Need vesiniksidemed fikseerivad pöörlemis-sammu ja kokkuvõttes moodustub aminohapetest spiraalne struktuur, nn. -spiraal (alternatiivne võimalus on siiski ka nn. -voldik).
Seega, valgu moodustumisel osalevad kõik eespool kirjeldatud kovalents-sidemete omadused, nagu - ja - konfiguratsioon, polariseeritus (elektronegatiivsus), doonor-aktseptor-iseloom, hübridiseerumisvõime, delokaliseerumine (resonants). Kuigi kvantmehaanika ei ole võimeline täpselt ette ennustama kõiki neid kombinatsioone, on tema abil nende esinemine vähemalt seletatav. See demonstreerib veel kord, kuivõrd olulised on kvantmehaanilised nähtused elu alusena. Pealegi, tundub, et sedalaadi kombineeritud sidemed võivad esineda ka molekulide vahel, avardades molekulaarstruktuuri mõistet kõrgematele organisatsioonitasemetele, ja miks mitte kuni organismi tasemeni välja. On ju väga raske uskuda, et pärilikkuse detailid, nagu näojooned, kõnnak, häälekõla jne. on ainult geenide ekspressiooni regulatsiooni tulemusel sünteesitud valkude erinevate koguste kombineerumise tulemus. Ehk on siingi mängus suunatud süntees, struktuuride laienemine kindlates suundades, mis on võimalik ainult molekulidevaheliste sidemete suunatuse tulemusena. Kursuse järgnevates osades vaatlemegi molekulide ühendusi, kuid siiski kõige lihtsamaid, neid mida füüsika seaduste alusel veel küllalt hästi kirjeldada saab. Need on gaasid, vedelikud ja tahkised üldises mõttes.
Gaasid
Aine on gaasilises olekufaasis kui molekulid ei ole omavahel seotud, vaid liiguvad vabalt ruumis, elastselt põrkudes nii omavahel kui nõu seintega. Elastsed põrked on niisugused, kus impulsi jäävuse seadus on rahuldatud, s.t. molekulide liikumise energiast osa ei muutu molekuli siseenergiaks (näiteks nagu piljardikuulide põrked). Nõu peab gaasi ümbritsema selleks, et molekulid ei liiguks ruumis laiali lõpmatu kaugele. Niisugusel nõus oleval gaasil on rida omadusi, mida saab mõõta ja mis on omavahel füüsikaseadustega seotud. Need omadused iseloomustavad mitte enam individuaalset molekuli, vaid molekulide kollektiivi tervikuna.
Gaaside näited. Toatemperatuuril on gaasilised ained näiteks H2, He, N2, O2, F, Ne, Cl, Ar. Tähtsaim on õhk, mis on gaaside segu (ruumala protsentides, kuiv õhk): N2 (28%), O2 (21%), Ar (1%), CO2 (0.037%). Tavaliselt aga on õhus veel veeauru kuni 2-3%, vastavalt siis teiste komponentide osa väheneb. Nagu näeme, võivad gaasid koosneda üheaatomilistest (n. väärisgaasid), kahe- ja kolmeaatomilistest molekulidest.
Gaasi mass. Gaasi hulga mõõtmiseks võib kasutada tema massi kilogrammides. Kuna erinevate gaaside üksikmolekulid on erineva massiga, siis erinevate gaaside puhul vastab ühele kg-le erinev hulk molekule. Gaaside füüsikaliste omaduste määramisel on aga molekulide arv ruumiühikus olulise tähtsusega. Seetõttu on massi mõõtühikuks sobiv valida niisugune, mis jätaks molekulide arvu konstantseks (loomulikult ei ole siis mass kg-des konstantne). Massi mõõdetaksegi seetõttu gramm-aatomites või gramm-molekulides (gramm-molekuli kutsutakse lühidalt mooliks). Gramm-molekul on aine hulk grammides, mis on arvuliselt võrdne selle aine molekulkaaluga. Gramm-aatom on siis vastavalt aine hulk grammides mis on arvuliselt võrdne selle aine aatomkaaluga. Aatomi ja molekuli kaalu määrab peamiselt tuuma(de) kaal. Tuumas on nii prootonid kui neutronid, kusjuures element (aine) on määratud prootonite je elektronide arvuga, neutronite arv ei ole aga päris kindel. Erineva neutronite arvuga kuid sama prootonite arvuga aineid nimetatakse isotoopideks, ja neil on vastavalt erinev aatom-mass. Seetõttu tuleb erinevate isotoopide segu puhul gramm-mooli arvuliseks väärtuseks lugeda keskmine aatom-mass. Aatom-massi ühikuks loetakse 1/12 süsiniku isotoobi 12C aatomi massist. See ühik on üsna lähedane vesiniku aatomi massile (väike erinevus tuleb sellest, et prootoni ja neutroni massid ei ole päris võrdsed, vesinikus aga neutron puudub). Keskmiste aatom-masside näited (sulgudes tähtsamad isotoobid, nurksulgudes radioaktiivsed, tehislikud):
H: 1.008(1,2,[3]); C: 12.011(12,13,[14]); N: 14.007(14,15); O: 15.999(16,17,18); P: 30(31,[ 32])
6800/1 98.89/1.108% 99.4/0.4% 99.76/0.037/0.204% 100%
Nagu näeme, on isotoopide segus domineeriv üks ja aatomkaalude erinevused täisarvudest on suhteliselt väikesed. Gaasidena esinevad H2, N2 ja O2, nende gramm-molekul on siis vastavalt 2, 28ja 32g ainet.
Kuna mooli mass suureneb proportsionaalselt ühe molekuli kaaluga, siis on moolis alati ühepalju molekule, sõltumata molekuli massist. See arv on 6.0228x1023 ja on tuntud Avogadro arvuna.
Gaasi olekuparameetrid
Kuna gaasis molekulid ei ole üksteisega seotud vaid liiguvad vabalt, põrkudes omavahel janõu seintega, siis on gaasi ruumala alati määratud seda mahutava nõu ruumalaga. Peale ruumala on gaasi olekuparameetriteks veel rõhk ja temperatuur. Rõhk on füüsikaline suurus, mida mõõdetakse pinnaühikule mõjuva jõuga, ühikuks on N/m2 = Pascal (Pa). Gaasi rõhk tuleneb sellest, et molekulid põrkuvad nõu seintelt tagasi, mõjutades sellega seinu (Newtoni III seadus). Temperatuur iseloomustab gaasi molekulide liikumise kineetilist energiat. Temperatuur on null kui molekulid on paigal ja kasvab võrdeliselt molekulide ruutkeskmise kiiruse ruuduga (E=mv2/2). Temperatuuri mõõdetakse Kelvinites (absoluutse temperatuuri kraadides), igapäevases elus aga Celsiuse skaala järgi, kus vee külmumistemperatuur loetakse 0° ja keemistemperatuur 100°. USAs mõõdetakse temperatuuri Fahrenheiti skaala järgi, mille kohaselt 0°C=???°F ja 100°C=???°F. Pange tähele, et ka temperatuuri puhul on ühikute süsteem ebajärjekindel, temperatuur ei võrdu ühe ühikuga kui molekulide kineetiline energia on üks J.
Gaasi olekuvõrrand
Kui gaasi ruumala vähendada sel teel, et nõu ruumala vähendatakse (näiteks kui kolb liigub silindris või kui pall jääb auto ratta alla), siis rõhk tõuseb pöördvõrdeliselt ruumala vähenemisega, nii et
![]()
Kui aga gaasi temperatuuri langetada jättes ruumala konstantseks, siis rõhk langeb võrdeliselt absoluutse temperatuuriga:
![]()
Neid kahte valemit saab kombineerida ja konstandile saab leida absoluutväärtuse, nii et saame seose, mida nimetatakse gaasi olekuvõrrandiks:
![]()
kus R on nn. ggaside universaalkonstant ja n on gaasi moolide arv vaadeldavas nõus. Gaaside universaalkonstandi väärtus on 8.3147 ja dimensioon on
![]()
Rakendades olekuvõrrandit arvutame ühe mooli gaasi ruumala 0°C ja 101300 Pa juures, mis on normaalne atmosfäärirõhk merepinnal.
![]()
Peame meeles, et ühe mooli gaasi ruumala standard-tingimustel (0°C, 101.3kPa) on 22.5 l. Rõhu tõustes see ruumala väheneb pöördvõrdeliselt rõhuga, temperatuuri tõustes suureneb võrdeliselt absoluutse temperatuuriga. Näiteks toatemperatuuril ja standardrõhul on mooli ruumala
![]()
Keemias kasutatakse ainete kontsentratsioonide väljendamiseks ühikut mooli/liitris (molaarsus, M). Mitmemolaarne on õhk toatemperatuuril? Kui üks mool on 24.15 l siis ühes liitris on 1/24.15=0.041 M = 41 mM. Kui suur on seejuures hapniku kontsentratsioon? [O2] = 0.21x41 = 8.61 mM. Kui suur on CO2 kontsentratsioon? [CO2]=0.000365x41= 0.0149 mM =15M.
Gaaside molekulaarkineetilise teooria alged
Gaaside molekulaarkineetiline teooria seob makroparameetrid (rõhk, temperatuur) molekulide energiaga. Tuletame näitena gaasi rõhu molekulide liikumise kiirusest.
Rõhu seos molekulide kineetilise energiaga. Gaasi rõhk nõu seinale tekib sellest, et molekulid põrkudes avaldavad seinale jõudu. Jõud mõjub tegelikult iga üksikpõrke ajal, aga suure hulga molekulide puhul hetkelised jõud keskmistuvad.
Olgu meil n molekuli kuubis küljega l. Kuigi nad liiguvad igasugustes suundades, vaatleme x, y ja z-suunalisi liikumise komponente eraldi. Iga molekuli põrkumisel risti seinaga (molekul ei põrku risti seinaga, vaid ainult vastavasuunaline komponent) tema liikumise hulk (impulss) muutub suuruselt mv suurusele –mv, seega 2mv võrra.
![]()
Kahe järjestikuse põrke vahelise aja leiame, arvutades selle kui aja, mille jooksul molekul liikus teise seinani ja sealt uuesti tagasi.
![]()
Kuigi molekul liikudes põrkub paljude teistega, võib impulsi jäävuse seaduse alusel ette kujutada, nagu liikumise x, y ja z-suunalised komponendid kanduksid üheklt molekulilt teisele üle ja kuigi lõpuks ei saabu seina juurde tagasi enam seesama molekul, on kulunud aeg siiski seesama, mis oleks olnud ühe molekuli likumisel ilma põrgeteta. Nüüd teeme olulise füüsikalise eelduse: teame küll, et molekuli põrge seinaga toimub momentselt, meie aga kujutleme, et põrkeprotsess keskmistus üle kahe põrke vahelise aja. Rakendame selle aja kohta eespool tuletatud seost impulsi muutuse ja jõu mõjumise aja vahel:
![]()
ehk asendades
![]() ,
,
kust
![]()
Kuna me keskmistasime põrkeprotsessi üle kahe põrke vaheaja, siis niisugune oleks keskmine jõud üle kahe põrke vaheaja, seega pidevalt mõjuv jõud, mis mudaks molekuli liikumise vastassuunaliseks. Newtoni kolmanda seaduse kohaselt mõjub samasuur jõud ka seinale. Meie kuubis küljega l oli n molekuli. Kuigi nad liiguvad kõikides suundades ja ainult liikumise komponendid on kuubi seintega risti, võib siiski kujutleda, et pilt oleks sama kui molekulidest n/3 liiguks iga seina suunas risti. Seega oleks kõigi molekulide poolt kuubi küljele avalduv jõud
![]()
Rõhu arvutamiseks tuleb jõud jagada külje pindalaga:
![]()
Paneme tähele, et n/l3=n0, mis on molekulide arv ruumalaühikus. Seega
![]()
Viimane valem eeldab, nagu liiguksid kõik molekulid ühesuguse kiirusega v. Kui molekulide kiirused on erinevad, tuleb arvutada kiiruste ruutude keskväärtus
![]()
ja asendades saame
![]()
Gaasi rõhk on võrdeline molekulide tihedusega ruumalaühikus ja ühe molekuli keskmise kineetilise energiaga. Kas dimensioonid klapivad?
![]()
Temperatuuri seos molekulide kineetilise energiaga. Olles sidunud rõhu molekulide kineetilise energiaga kasutame edasi gaaside olekuvõrrandit, mis seob rõhu temperatuuriga. nII saame temperatuuri siduda molekulide kineetilise energiaga. Kuna
![]()
siis võime viimase valemi kirjutada kujul
![]()
Siin l3 on nõu ruumala n on selles nõus olevate molekulide arv. Kui võtame molekulide arvuks ühe mooli ehk n = Na, siis on nõu ruumala võrdne mooli ruumalaga V0 ja selle rõhk on seotud temperatuuriga olekuvõrrandi kaudu:
![]()
Valemi keskmises liikmes on ühe mooli gaasi kõigi molekulide kineetiliste energiate summa, Ek
![]()
Seega,
![]()
Oleme leidnud väga tähtsa suuruse, ühe mooli gaasi keskmise kineetilise energia sõltuvalt temperatuurist. Tuletaud seos on õige kerakujuliste molekulide jaoks, mis liiguvad ainult translatoorselt, kuid ei sisalda võnke- ega pöörlemisenergiat. Tegur 3/2 tuleneb sellest, et iga teljesuunaline liikumise komponent kannab energiat RT/2. Kaheaatomsetes molekulides võivad aatomid (lisaks molekuli translatoorsele liikumisele) veel omavahel võnkuda ja tiirelda. Need kas viimast liikumisvõimalust kannavad ka kumbki sellesama hulga energiat, RT/2, ja kaheaatomse molekuliga gaasi mooli koguenergia on seega 5/2RT. Niisugust liikumisvõimaluste arvu nimetatakse molekulide vabadusastmete arvuks ja see mäarab, kui palju energiat tuleb kokku kulutada gaasi temperaturi tõstmiseks ühe kraadi võrra või kui palju seda vabaneb gaasi jahtumisel. Peame meeles suuruse RT väärtuse toatemperatuuril:
![]()
Selle
suurusega tuleb võrrelda keemilistes reaktsioonides mooli
kohta vabanevat või nõutavat energiat, et mõista
nende kulgemise võimalikkust. Võrdleme seda suurust
veel energiaga elektronvoltides. Elektronvolt oli töö, mida
tuli teha, et elektron viia ühe voldi võrra
negatiivsemale potentsiaalile: 1eV=1.602x10-19 J. Kui
viime terve mooli elektrone 1V võrra kõrgemale
energiale, teeme tööd 1.602x10-19x6.023x1023=96480
J mol-1V-1. See arv on tuntud Faraday arvuna ja
tähistab tööd, mida tuleb teha, et üks mool
elektrone viia läbi potentsiaalide vahe 1V. Võrreldes
sellega on RT väike suurus, RT(V) =
2436/96480=0.0253V = 25.3 mV. Bioloogiliselt tähtsad
potentsiaalide vahed raku- ja mitokondrite membraanidel on 50-150 mV,
seega 2 kuni 6RT. Võrdleme RT veel valguse kvandi
energiaga. Punase kvandi energia oli 1.8 eV, seega kukkus elektron
punat kvanti kiirates 1.8V võrra. Punase valguse lainepikkus
on 680 nm. RT (25.3mV) moodustab ainult 1.4% punase kvandi energiast.
RT võrra erinev energia väljenduks lainepikkuse muutusena
1.4% võrra ehk 9.6 nm võrra. Kuna keskmiselt nii suur
energia on toatemperatuuril pidevalt olemas ja kandub orbitaalidele
üle molekulide põrgetes, siis ei saagi aatomid
(molekulid) kiirata enam kindlat lainepikkust vaid ribade laiuseks
kujuneb keskmiselt ±10 nm. Energiale 2436 J/mol vastaks õhus
molekulide ruutkeskmine kiirus ![]() kust v = 410 m s-1 (siin M on mooli mass,
õhu puhul ligikaudu 0.029 kg).
kust v = 410 m s-1 (siin M on mooli mass,
õhu puhul ligikaudu 0.029 kg).
Kuigi tuletasime temperatuuri ja molekulide liikumise kineetilise energia vahelise seose gaaside jaoks, on temperatuuride tasakaalu korral energiad vabadusastme kohta võrdsed ka vedelikes ja tahketes kehades (tahkistes). Molekulide vabadusastmete arv gaasides, vedelikes ja tahkistes on aga erinev.
Soojamahtuvus, erisoojusEelnevast on selge, kui palju energiat tuleb kulutada ühe mooli gaasi soojendamiseks ühe kraadi võrra. Sõltuvalt vabadusastmete arvust (molekuli ehitusest) on see kas 3/2RT või 5/2RT. kus T tähistab temperatuuri tõusu. Saadud väärtus on aga õige ainult juhul, kui gaasi ruumala jääb soojenedes samaks ja rõhk seejuures tõuseb. Seetõttu tuleb alati täpsustada, et tegu on mooli soojamahtuvusega ehk erisoojusega Cv konstantse ruumala puhul. Kui me soojendame gaasi ja lubame tal seejuures paisuda, näiteks nii et rõhk jääb konstantseks, siis teeb paisuv gaas lisaks veel tööd, tõugates seinu eemale rõhuga p. Gaasi paisumisel tehtud töö on pV. Teame aga, et ühe mooli gaasi puhul
![]()
Arvestades ka gaasi paisumisel tehtavat tööd tuleb konstantsel rõhul (suurenrval ruumalal) gaasi soojendamisel teha rohkem tööd: üheaatomse gaasi puhul 3/2RT+ RT=5/2RT ja kaheaatomse gaasi puhul 5/2RT+RT=7/2RT. Seega on gaasi erisoojus konstantsel rõhul (Cp) suurem kui konstantsel ruumal (Cv). Kasutatud soojusenergiast suurem osa (üheaatomsete gaaside puhul 60%) jääb gaasi siseenergiaks (molekulide kineetiliseks energiaks), ja väiksem osa (40%) teeb kasulikku mehaanilist tööd. Niimoodi töötavad kõik soojusmasinad, näiteks automootorid, kus bensiini põlemise teel soojendatakse silindris olevat gaasi ja lastakse sel siis paisuda kolvi alla liikudes ja autot edasi lükata. Ülaltoodust on ka näha, et mida suurem on suhe Cp/Cv seda suurem on gaasi soojendamisel tehtava mehaanilise töö osa võrreldes kogu kulutatud energiaga. Üheaatomsetel gaasidel on see suhe 5/3 kaheaatomsetel aga 7/5.
Gaasi kokkusurumisel tehtav töö.
Eelmises lõigus võtsime teadmiseks, kuidas gaasi kokkusurumisel (paisumisel) tehtav töö sõltub gaasi ruumala muutusest. Tuletame siiski selle valemi. Töö on jõu ja jõu suunas käidud teepikkuse korrutis. Gaasis mõjub nõu pinnaühikule jõud p. Mingile pinnale S mõjub jõud pS. Kui kujutleme, et see pind on nagu kolb, mis võib liikuda rõhu mõjul, siis liikudes teepikkuse s võrra tehakse tööd pSs. Aga Ss=V ja tehtud töö ongi A=pV. Liikumist komponentideks jagades ei jäävad määravaks ainult pinnaga ristisuunalised komponendid ja gaasi nõu kuju muutustele viivad tangentsiallkomponendid tööd ei tee. Seega, ei ole tähtis, kuidas ruumala muutub ja missugused on seejuures toimuvad nõu kuju muutused. Küll on aga oluline, et gaasi rõhk jääks ruumala suurenemisel samaks. See on aga võimalik ainult siis kui gaasi samal ajal soojendada.
Kui me aga surume gaasi kokku ja seda ei soojenda, vaid hoopis hoiame temperatuuri konstantsena, siis kokkusurumisel paratamatult gaasi rõhk tõuseb. Selles protsessis tehtava töö arvutamiseks tuleb rakendada integreerimist. Elementaartöö väikesel ruumala muutusel
![]()
Aga gaasi olekuvõrrandist saame rõhu avaldada ruumala kaudu:
![]() .
.
Asendades ja tuues konstantsed liikmed integraali ette saame
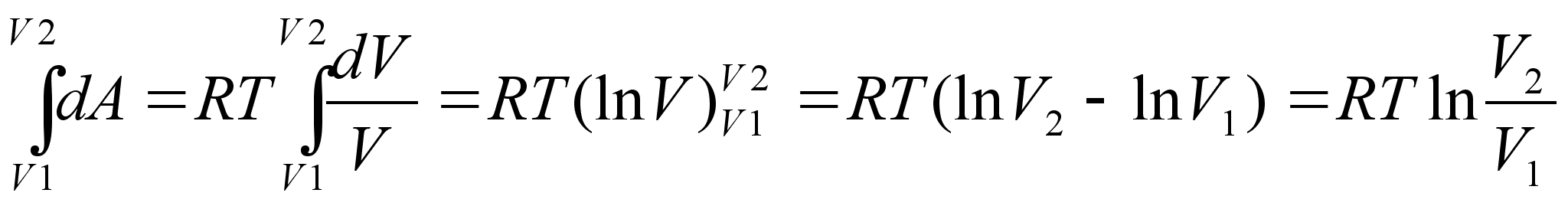
Gaasi oleku võrrandit kasutades saab avaldada sellesama töö ka alg ja lõpprõhkude kaudu:
Kuna konstantsel temperatuuril rõhk ja ruumala on pöördvõrdelised,
![]() ,
,
siis
![]()
Viimast valemit kasutame allpool, et leida rakumembraanil ainete kontsentratsioonide erinevusest tulenevat energiat, nn. membraani eneergiseritust. Tuletame meelde, et see valem esitab gaasi paisumistöö (kokkusurumistöö) konstantsel temperatuuril, samal ajal kui valem ?? esitas selle konstantsel rõhul.
Adiabaatne protsess.
Mõlemad ülalkäsitletud protsessid nõuavad pidevat gaasi temperatuuri jälgimist ja välise soojuse või jahutaja kaudu reguleerimist, sest neis mõlemis peab temperatuur igal juhul konstantne olema. Jalgratta- või autikummi pumbates oleme täheldanud, et pump kuumeneb, kuigi me seda otse ei soojenda, vaid ainult surume gaasi kokku. Me lihtsalt ei jahutanud pumpa küllalt kiiresti, et hoida temperatuuri konstantsena. Niisuguseid protsesse gaasidega, kus väline soojusvahetus on täielikult välditud, nimetatakse adiabaatseteks. Gaasi adiabaatsel kokkusurumisel gaasi temperatuur tõuseb. See tuleb sellest, et kokkusurumisel seinad liiguvad sissepoole ja seintelt tagasi põrkuvad molekulid suurema kiirusega kui nad seintele lähenesid, s.t., seina liikumise kiirus liitb molekuli liikumise kiirusele. Kokkuvõttes gaasi molekulide kineetiline energia suureneb. Gaasi ruumala vähendamisel on effekt vastupidine, tagasi põrkudes molekulid aeglustuvad. Selle tulemusena on adiabaatne protsess üsna keerukas: gaasi kokku surudes rõhk tõuseb kõigepealt ruumala vähenemise tõttu, aga lisaks veel temperatuuri tõusu tõttu, seega adiabaatses protsessis rõhk muutub rohkem kui isotermilise protsessi korral. Lahustes toimuvates protsessides, mis on bioloogias peamised, on temperatuur tavaliselt konstantne ja adiabaatseid nähtusi esineb harva.
Molekuli suurus, molekulidevaheline kaugus, vaba tee pikkus
nII
kaua kui gaasi kokkusurumisel molekulide elektronkatted ei asu
pidevalt üksteise mõjusfäaris (molekulid ei ‘puutu
kokku’), on rõhu ja ruumala vaheline sõltuvus
vastavuses gaasi olekuvõrrandiga. Rõhk tõuseb
ainult sellepärast, et molekulide tihedus ruumalaühikus
suureneb ja nad hakkavad tihedamini seinaga põrkuma. Öeldakse,
et gaas käitub nagu ‘ideaalne gaas’, mille molekulid
on nii väikesed, et kokkusurumist veel ei takista. Vaatame, kui
suured on molekulid põrkumisraadiuse seisukohast. Võtame
näiteks vee molekuli. Vedelas olekus on ühe mooli vee mass
18 g ja ruumala 18 cm3. Seega, Na
molekuli täidavad 18 cm3. Ühe molekuli all olev
ruumala on 18/6.023x1023= 2.989x10-23 cm3.
Sellise ruumalaga kuubi külje pikkus oleks ![]() 3.10x10-8
cm = 3.10 A. Põrkeraadius oleks seega 1.55 A. Ka teiste õhus
olevate gaaside molekulide põrkeraadiused on samas
suurusjärgus. Toatemperatuuril on õhu moolruumala 24.15 l
= 0.02415 m3. Ühe molekuli kohta tuleb ruumala
0.02415/Na = 4.0096x10-26 m3, vastav kuubi külg
oleks
3.10x10-8
cm = 3.10 A. Põrkeraadius oleks seega 1.55 A. Ka teiste õhus
olevate gaaside molekulide põrkeraadiused on samas
suurusjärgus. Toatemperatuuril on õhu moolruumala 24.15 l
= 0.02415 m3. Ühe molekuli kohta tuleb ruumala
0.02415/Na = 4.0096x10-26 m3, vastav kuubi külg
oleks ![]() Molekulide
keskmine kaugus õhus on umbes kümme korda suurem kui
nende diameeter. Õhku tuleks umbes 1000 korda kokku suruda, et
molekulid läheneksid kokkupuuteni (molekulidevaheline kaugus
väheneb kuupjuurega ruumalast). See on ka piir mille juures
ülaltoodud gaaside olekuvõrrand kehtivuse kaotab. Täpsuse
kaotab ta aga juba kümme korda madalamal rõhul, mõnede
gaaside puhul, nagu CO2 ja veeaur, isegi palju varem.
Molekulide
keskmine kaugus õhus on umbes kümme korda suurem kui
nende diameeter. Õhku tuleks umbes 1000 korda kokku suruda, et
molekulid läheneksid kokkupuuteni (molekulidevaheline kaugus
väheneb kuupjuurega ruumalast). See on ka piir mille juures
ülaltoodud gaaside olekuvõrrand kehtivuse kaotab. Täpsuse
kaotab ta aga juba kümme korda madalamal rõhul, mõnede
gaaside puhul, nagu CO2 ja veeaur, isegi palju varem.
Tähtis
gaasi parameeter on veel molekuli keskmine vaba tee pikkus, keskmine
liikumisruum põrkest põrkeni. See määrab
näiteks difusiooni kiiruse. Olgu meil gaas kus on n
molekuli m3 kohta. ühe molekuli raadius olgu r.
Lihtsustuseks kujutleme, et molekul liigub sirgjoneliselt ja lööb
põrgetel teised molekulid eemale ise trajektoori muutmata.
Niimoodi liikudes puudutab molekul kõiki teisi, mis asuvad
silindris raadiusega 2r. Kui molekul liigub 1 m pikkuse tee,
siis puudutab ta molekule, mille keskpunktid asuvad silindris
ruumalaga ![]() m3, ja neid oli
m3, ja neid oli ![]() .
Kuna 1 m tweepikkusel oli nimitu põrget, siis iga põrke
vaheline keskmine vaba tee pikkus oli
.
Kuna 1 m tweepikkusel oli nimitu põrget, siis iga põrke
vaheline keskmine vaba tee pikkus oli
![]() ,
,
kus d tähistab molekuli põrkediameetrit. Täpsem arvutus, mis arvestab ka põrgetel toimuvat trajektoorimuutust, annab veidi suurema keskmise vaba tee pikkuse:
![]()
Arvutame järgmiste andmetega:
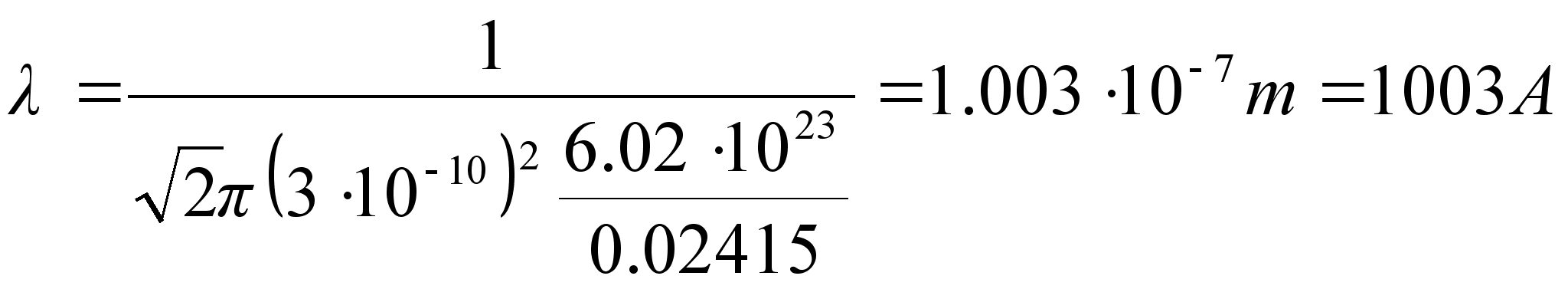
Molekuli vaba tee keskmine pikkus on 1000 A =100 nm, kui molekulide keskmine kaugus on 33 A ja diameeter 3 A.
Difusioon
Nagu nägime, on molekulide kiirus toatemperatuuril üle 400 m/s ja põrkumisteta kataksid nad ka sellesama vahmaa sekundi jooksul. Tegelikult nad põrkuvad ja muudavad liikumise suunda iga 100 nm järel, mille tulemusena nende tegelik edasiliikumine ruumis on juhuslik ja tunduvalt aeglasem. Aga nad liiguvad siiski ja niisugune molekulide juhuslik ümberpaiknemine ruumis kannabki nimetust difusioon. Difusioonil on bioloogias suur tähtsus, olles peamine ainete transpordi mehhanism raku piires, samuti taime ja keskkonna vahel. Difusiooniprotsessis molekulid liiguvad juhuslikult igas suunas. Seejuures kõrgema tihedusega (kontsentratsiooniga) piirkondadest eemale toimub likumine suurema tõenäosusega kui madalama kontsentratsiooniga piirkondadest kõrgama kontsentratsiooniga piirkondadesse. Niimoodi toimub difusiooni käigus aine kontsentratsiooni ühtlustumine. On loogiline, et molekulide difusiooniline ümberpaiknemine ruumis toimub seda kiiremini, mida kiiremini molekulid liiguvad ja mida suurem on kskmine põrgetevahelise vaba tee pikkus. Kontsentratsiooni ühtlustumine toimub seda kiiremini, mida järsem on kontsentratsiooni muutus ruumis, s.t., mida suurem on kontsentratsiooni gradient. Gradient on mingi pideva suuruse muutumise kiirus ruumi koordinaadi järgi.
Näiteks toome valemi difusioonikiiruse kohta silindrilises torus, kus ühes otsas hoitakse kontsentratsiooni C1 ja teises otsas C2, toru pikkus on l ja ristlõikepindala on s:
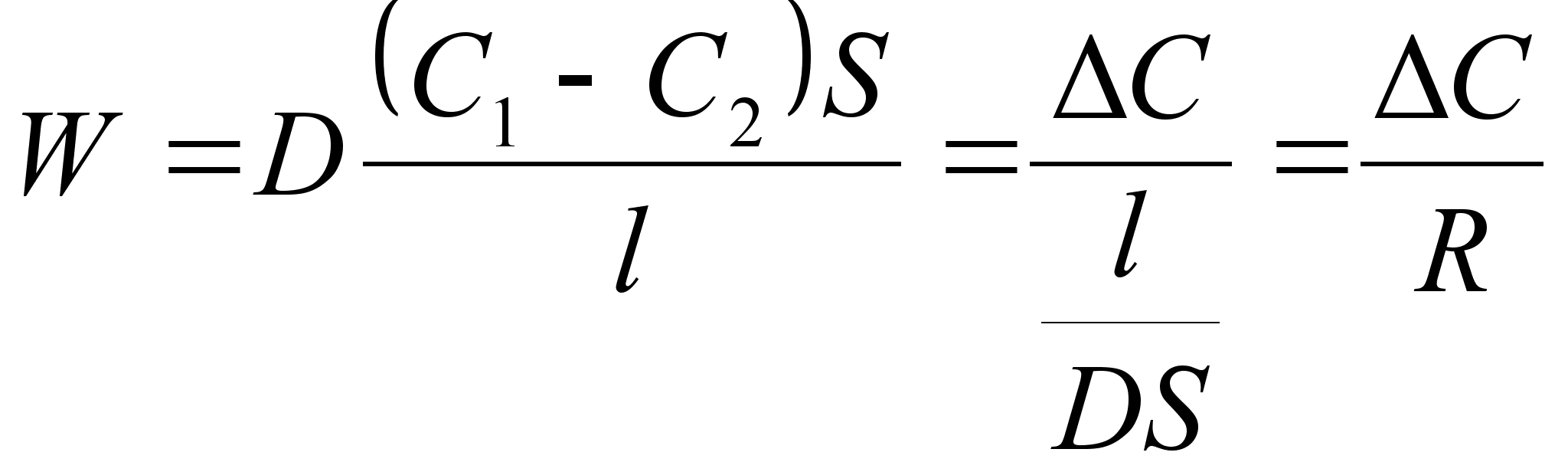
kus
![]()
Nendes valemites l ja S on geomeetrilised parameetrid, mis iseloomustavad difusiooniteed, difusioonikonstant D aga iseloomustab difundeerivat ainet ja difusioonitingimusi:
![]()
Nagu näeme, on difusioonikonstant sõltuv molekulide lineaar-keskmisest kiirusest ja vaba tee pikkusest, kordaja 1/3 tuleneb jällegi sellst, et liikumist vaadeldakse iga koordinaadi suunas eraldi. Difusioonikiiruse valem, nn Fick’i seadus, on sarnane Ohmi seadusele, mis määrab elektrivoolu kiiruse läbi takistust omava traadi.
Difusiooni kiirus ajas ja ruumis
Eelnevad seosed võimaldavad arvutada difusioonivoo kiirust ruumis konstantse kontsentratsioonivahe (või gradiendi) puhul. Gradiendi konstantsuse säilitamiseks peab molekule pidevalt kuhugi ära kaduma. Näiteks, taimelehes süsihappegaas pidevalt neeldub fotosünteesi käigus ja seetõttu säilib lehes madalam CO2 kontsentratsioon kui välisõhus. Kui molekule ära ei kao, siis esialgu tekitatud kontsentratsioonivahe kaob mõninga aja pärast. Aga kui kiiresti see toimub? Difusioonilise liikumise kiiruse teadmine võimaldab hinnata kui kiiresti molekulid raku sees ümber paiknevad.
Vaatleme lihtsuse mõttes ühemõõtmelist juhtu. Oletagem, et sünteesisime mingi kogse metaboliiti raku keskel asuval tasandil ja küsime, kui kiiresti see difundeerub rakus laiali? Tuletame kõigepealt meelde Fick’i seaduse statsionaarse difusioonivoo J kohta ja defineerime voo tiheduse:
![]()
Siin dC/dx on kontsentratsiooni gradient e. kontsentratsiooni muutumise kiirus x-telje suunas, J on defineeritud kui aine voo tihedus, mida mõõdetakse pinnaühikut ajaühukus läbinud aine hulgaga, seega mooli m-2 s-1. Voo tiheduse mõiste sissetoomine võimaldab Fick’I seaduse lihtsasti kirjutada, ilma difusioonitee pikkust ja ristlõiget kasutamata.Valime kaugusel x meie tasapinnast, kus aine eraldus, ühe ühikulise pindalaga ruudu ja selle kõrvale kaugusele x+dx kohe teise ruudu, nii et saame nagu õhukese kasti (Joonis). Kohal x, kasti sisenedes, on voo tihedus J, kohal x+dx, kastist väljudes, on voo tihedus muutunud. Kuna see muutus on väike, kasutame Taylori ritta arendust ja avaldame
![]()
Kuna väljavoolukiirus ei võrdu sissevoolukiirusega, peab kasti ainet kogunema (või sealt kaduma), sest ruumilisi neeljaid me praegu ei arvesta. Meie ühikulise pinnaga kastikeses olgu aine hulk alguses Cdx (C on kontsentratsioon, pindala=1). See muutub tänu aine kogunemisele (lahkumisele) järgmise kiirusega
![]()
Pärast dx ja J taandamisi saame nn. pidevuse seaduse:
![]()
![]()
Seadus põhineb aine jäävusel ja väidab, et kui voo tihedus ruumis muutub, siis aine koguneb. Asendame nüüd J Fick’i seadusest
![]()
See on difusiooni üldine ajalis-ruumiline diferentsiaalvõrrand. Kolmemõõtmelisel juhul tuleb teised tuletised võtta kolme koodinaadi suunas. Meie ühemõõtmelisel juhul on selle võrrandi lahendiks funktsioon
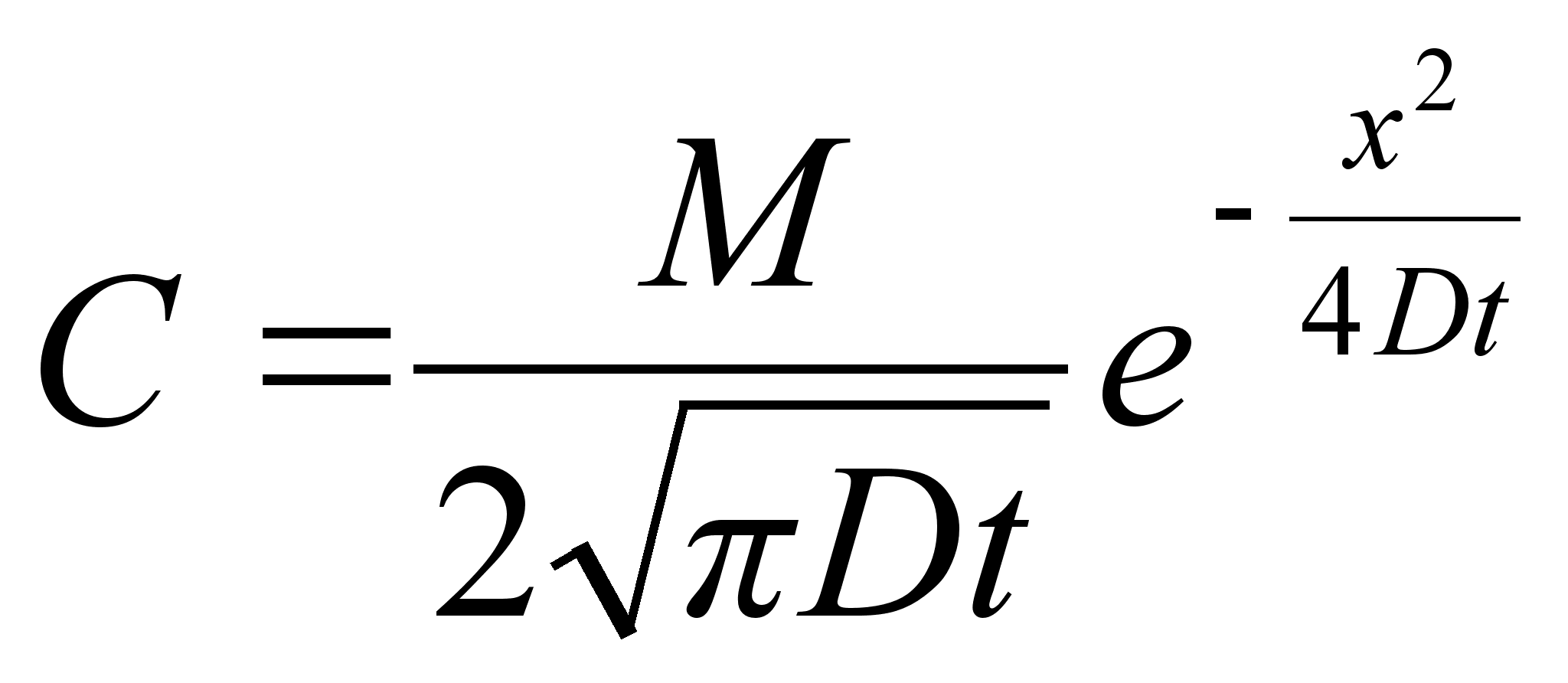
Kus M on aine kogumass, mis eraldus protsessi alguses tasapinnal x = 0.
Võrrandi lahend on eksponent, mis kahaneb x kasvades ruumis kiiresti, kuid ulatub siiski kõikjale, seega peame konkretiseerima küsimust, ‘kui kaugele aine difundeerub mingi aja jooksul’. Utleme, et meid huvitab, kui kaugel on frondi kõige järsem osa, seal kus funktsiooni väärtus on e-1=0.36. Tingimus, et e astendaja = 1 tähendab, et
![]() või
või ![]()
Difusioonifrondi levides selle kõige järsem koht kaugeneb võrdeliselt ruutjuurega ajast, näiteks 2 korda kui aeg kasvab neli korda. Aeg, mis kulub mingi distantsi läbimiseks kahaneb võrdeliselt kauguse ruuduga. Siit tulenebki, et väikestel distantsidel on difusiooniline transport efektiivne, kuid kaotab efektiivsuse distantsi kasvades väga kiiresti.
Anname mõned difusioonikonstandi väartused (ühikutes cm2s-1):
Vees: suhkur 0.52 10-5 Õhus: CO2 0.16
glükoos 0.67 veeaur 0.24
glütsiin 1.1 O2 0.20
Ca(Cl)2 1.9
Proteiin 0.1
DNA 0.01
Rusikareegel on, et õhus on difusioonikiirused ligikaudu 10000 korda suuremad kui vees. Vahe tuleneb väga väikesest molekuli vaba tee pikkusest vees võrreldes gaasiga. Raskemad molekulid difundeeruvad aeglasemalt, sest nende liikumise kiirused on väiksemad, kuna samal temperatuuril on energiad samad, suurema massiga molekulid aga liiguvad aeglasemalt. Kui võtame difusioonikonstandiks 10-5 cm2 s-1 siis difundeerumiseks kulub järgmine aeg:
5 m (raku organellid) 0.006 s = 6 ms
50m (rakud) 0.6s
1 m (organism) 8 aastat
Nagu näeme, on organellis difusioonikiirus sedavõrd suur, et molekul võib umbes 200 korda sekundis läbi organelli difundeeruda. Terve raku mõõtmes on see aga ainult paar koda sekundis. Difusiooniline ainete transport organismi piires on aga lootusetult aeglane. Seetõttu metaboliitide kaugtransport toimubki peamiselt voolamise abil, närvierutus aga liigub elektri-impulsside abil.
Soojusjuhtivus
Tahkes kehas on eriti hästi näha, et soojendades keha ühte osa jõuab soojus varsti jaguneda ühtlaselt üle kogu keha. Soojus nagu difundeeruks laiali. Sama toimub ka gaasides ja see ongi kehade soojusjuhtivus. Kuna soojus on põhimõtteliselt molekulide kineetiline energia, siis selle ‘laialidifundeerumine’ tähendab energia ülekannet põrgetel, kus kiiremini liikuvad molekulid jagavad oma energia teiste molekulidega. Nii kujuneb kehas lõpuks üsna ühtlane molekulide kiiruste jaotus. Et soojusjuhtivuse mehhanism on difusioonile sarnane, siis on ka vastavad valemid sarnased. Näiteks soojuse liikumine läbi varda pikkusega l ja ristlõikepinnaga S on
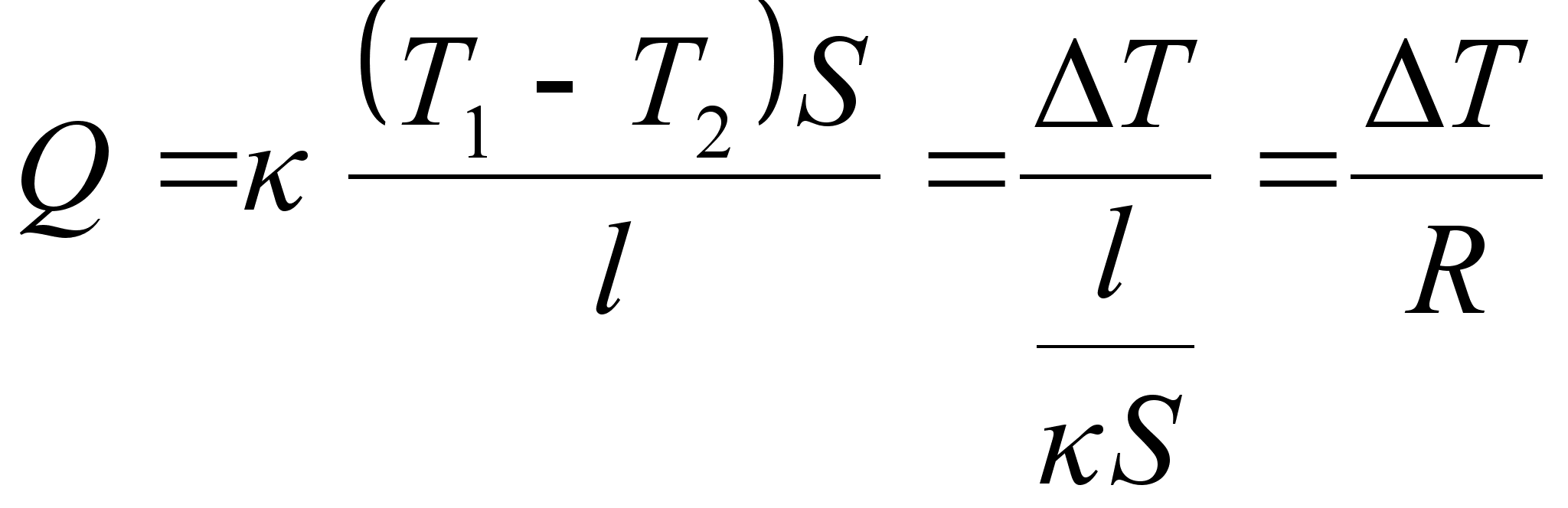
kus kontsentratsioonide vahet asendab temperatuuride vahe ja difusioonikonstanti soojusjuhtivuse konstant
![]()
Soojusjuhtivuse
konstant on difusioonikonstant korrutatud erisoojusega, mis on
tihedus korda massiühiku soojusmahtuvus ![]() .
.
Sisehõõrdumine, viskoossus
Voolamine on molekulide samaaegne ühesuunaline liikumine. Voolamine toimub näiteks torudes rõhkude vahe mõjul. Elusolendites toimub voolamine veresoontes loomadel ja juhtsoontes (ksüleem, floeem) taimedel. Voolamine on peamine viis molekulide transportimiseks pikematel distantsidel kui ühe raku piires. Voolamine võib olla laminaarne ja turbulentne. Laminaarse voolamise puhul vedeliku või gaasikihid torus segunevad ainult difusiooni tõttu, seega vähe, ja kihid, mis alustasid teekonda toru seinte lähedal, on seal toru lõpuni. Molekulid, mis alustasid teekonda toru keskosas jäävad samuti sinna kuni lõpuni. Laminaarne voolamine on tavaline peentes torudes, nagu kapillaarsooned ja taimede juhtsooned. Tubulentsel voolamisel toimub pidev keeriseline liikumine toru sees, selgeid kihte asendavad keerised, milles molekulid liiguvad kord sente lähehedale, kord jälle kaugemale. Turbulentne voolamine on tavaline jämedates torudes. Vaadake näiteks korstnast väljuvat suitsu, aga sarnane keeriselisus on ka vere voolamisel jämedamates veresoontes.
Ka voolamine allub sama tüüpi proportsionaalsele seadusele nagu difusioon ja soojusjuhtivus, ainult siin on liikumapanevaks jõuks rõhkude vahe:
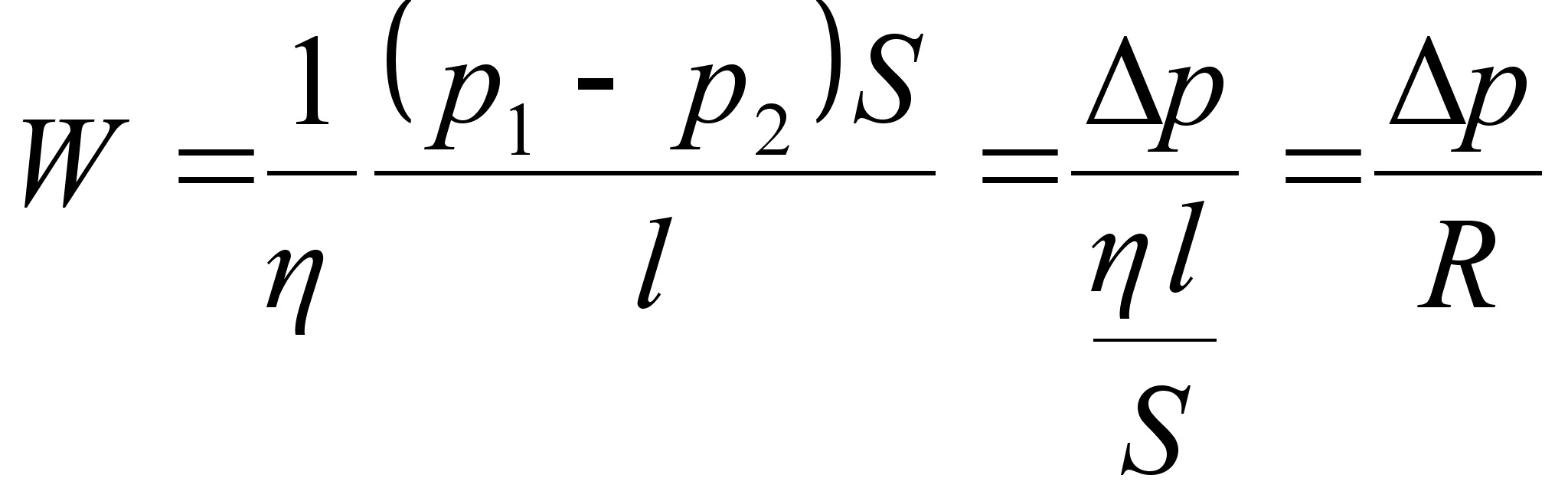
Pange tähele, et voolamise puhul on tavaks võrdetegurit esitada pöördsuurusena, viskoossusena. Mida suurem on viskoossus , seda aeglasem on voolamine sama rõhkude vahe ja sama voolu geomeetria puhul. Vedelike puhul on viskoossus põhjustatud peamiselt molekulidevahelistest sidemetest (tõmbejõududest). Kuna need temperatuuri tõustes nõrgenevad (molekulid liiguvad kiiremini ja kaugenevad üksteisest, keha paisub), siis vedelike viskoossus temperatuuri tõustes väheneb, voolamine kiireneb. Gaaside viskoossus põhineb teisel alusel, kuna nendes molekulidevahelised tõmbejõud ei ole tähtsad. Toru seinte lähedal liikuvad molekulid põrkuvad sageli seintega ja nende edasiliikumine piki toru on takistatud. Soojusliikumine aga pillutab molekule ka toru seintest eemale ja vastupidi, eemal olevaid molekule seinte suunas. Nii jäavad seinte poolt tulevad molekulid tsentri pool liikuvatele jalgu ja pidurdavad neid, aga tsentrist seinte poole liikuvad molekulid kiirendavad seinte lähedal asuvate voolusuunalist likumist. Kujuneb välja keskmine kiiruste profiil, mis on ruuthüperbooli kujuga, kusjuures kõige kiiremini voolavad molekulid toru keskel ja seinte äares on need peaaegu paigal (voolamise mõttes, mitte termilise liikumise mõttes). Kuna gaaside puhul viskoossus on tingitud molekulide difusioonist risti voolu suunaga, on ka viskoossustegur seotud molekulide soojusliikumise keskmise kiirusega ja vaba tee pikkusega:
![]() ,
,
kus on gaasi tihedus. Viskoossus ei sõltu gaasi rõhust, kuna rõhu suurenedes tihedus küll kasvab, kuid vaba tee pikkus proportsionaalselt kahaneb.
Ļīõīęčå šąįīņū
... . Żņč ļīķ˙ņč˙ īņšąęąžņ ļščšīäó īńķīāķūõ āēąčģīäåéńņāčé č ēąźīķīā äāčęåķč˙ ģąņåščč, ÷ņī, źąź čēāåńņķī, ńīńņąāė˙åņ ļšåäģåņ ōčēčźč – źąź ōóķäąģåķņąėüķīé åńņåńņāåķķīé ķąóźč. Ā öåķņšå āķčģąķč˙ įčīōčēčźč źąź įčīėīćč÷åńźīé ķąóźč ėåęąņ įčīėīćč÷åńźčå ļšīöåńńū č ˙āėåķč˙. Īńķīāķą˙ ņåķäåķöč˙ ńīāšåģåķķīé įčīōčēčźč – ļšīķčźķīāåķčå ķą ńąģūå ćėóįīźčå, żėåģåķņąšķūå óšīāķč, ńīńņąāė˙žłčå ģīėåźóė˙šķóž īńķīāó ...
... Ščńóķīź Źčķåņčźą įčīļšīöåńńīā Äčķąģč÷åńźčå ńāīéńņāą įčīļšīöåńńīā Źąęäą˙ ńčńņåģą ńīńņī˙łą˙ čē żėåģåķņīā įóäåņ õąšąźņåščēīāąņüń˙ äčķąģčźīé, ńźėąäūāąžłåéń˙ čē żėåģåķņīā. Źčķåņčźą įčīļšīöåńńīā – šąēäåė įčīōčēčźč, čēó÷ąžłčé äčķąģč÷åńźčå ńāīéńņāą įčīļšīöåńńīā. 1. Ļąšąģåņšū, ģåķ˙žłčå ńāīå ēķą÷åķčå ńī āšåģåķåģ. Ļåšåģåķķūå āåėč÷čķū: ÷čńėåķķīńņü źėåņīź, įčīģąńńą, źīķöåķņšąöč˙ ...
... ųźīėą, 1988. 10. Ąšņžõīā Ā.Ć., Źīāąėåāą Ņ.Ą., Ųģåėåā Ā.Ļ. Įčīōčēčźą. Āīšīķåę: Āīšīķåęńźčé ćīń. óķ-ņ 1994. 11. Ąķņīķīā Ā.Ō. Įčīōčēčźą. VI.: Ąšźņīń-Āčźąļšåńń, 2000. 12. Äīļīėķčņåėüķą˙ 13. Ģåõąķčźą č įčīģåõąķčźą 14. Ķčźčņčķ E. VI. Ņåīšåņč÷åńźą˙ ģåõąķčźą. VI.: Ķąóźą. 1968. Ąėåźńąķäåš Š. Įčīģåõąķčźą. VI.: Ģčš. 1970. 15. Ęóšąāėåāą Ą.Č., Išąåāńźą˙ Č.Ä. Ńļīšņčāķą˙ ģåäčöčķą č ėå÷åįķą˙ ...
... ńļīšņą ķą āūķīńėčāīńņü (ńļšąāą). Āūįīšźč ąķąėīćč÷ķū ļī ÷čńėó īįńėåäīāąķķūõ (65 ÷åėīāåź), ńīīņķīųåķčž ėčö ęåķńźīćī č ģóęńźīćī ļīėą (45-55%) č āīēšąńņó (18,1 ± 2,3 ćīäą) Ščń. 2į. Šåēóėüņąņū źėąńņåšķīćī ąķąėčēą äė˙ ćšóļļū āūńīźīźāąėčōčöčšīāąķķūõ ńļīšņńģåķīā ÓĪŠ-2 Ń.-Ļåņåšįóšćą (äčšåźņīš - Č.Č. Źīģąšīā). Ļī īń˙ģ īņėīęåķū ĆŠĀ ļąšąģåņš JSL äė˙ ėåāīé šóźč č äčńļåšńč˙ żņīćī ļąšąģåņšą DJSR äė˙ ļšąāīé ...
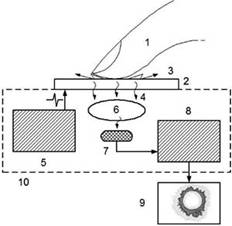
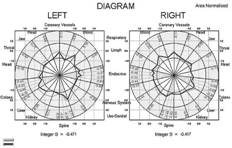
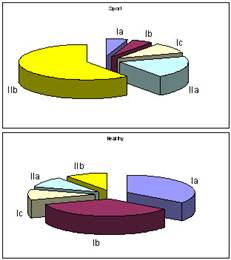
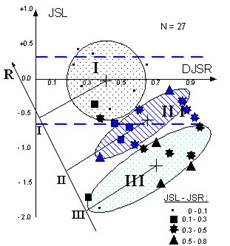
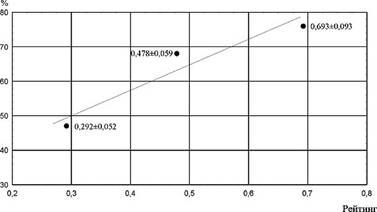
0 źīģģåķņąščåā