Движение заряженных частиц

Содержание 1. Движение электрона в равномерном магнитном поле, неизменном во времени и направленном перпендикулярно скорости……………………..3

2. Движение электрона в неизменном во времени магнитном поле, когда скорость электрона не перпендикулярна силовым линиям……………….4

3. Фокусировка пучка электронов по­стоянным во времени

магнитным полем (магнитная линза)……………………………………….6

4. Движение электронов в равномерном электрическом поле. Принцип работы электронного осциллографа………………………………………...7

5. Фокусировка пучка электронов постоянным во времени

электриче­ским полем (электрическая линза)……………………………….8

6. Движение электрона в равномерных, взаимно перпендикулярных, неизменных во времени магнитном и электрическом полях………………9

7. Движение заряженных частиц в кольцевых ускорителях………………11

Движение заряженных частиц в магнитном и электрическом полях

1. Движение электрона в равномерном магнитном поле, неизменном во времени и направленном перпендикулярно скорости.

В данных разделах под заряженной частицей мы будем подразумевать электрон. Заряд его обозначим q=-q_э  и массу m. Заряд примем равным q_э=1,601^.10^-19 Кл, при скорости движения, значительно меньшей скорости света, масса m=0,91^.10^-27 г. Полагаем, что имеет место достаточно высокий вакуум, так что при движении электрон не сталкивуается с другими частицами. На электрон, движущийся со скоростью в магнитном поле индукции,  действует сила Лоренца .

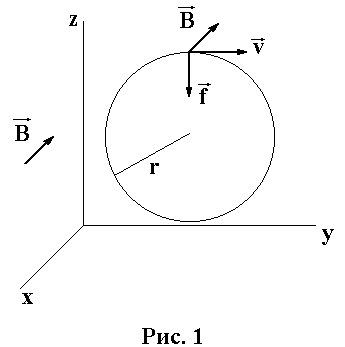На рис 1 учтено, что заряд электрона отрицателен, и скорость его направлена по оси y, а индукция по оси- x. Сила направлена перпендикулярно скорости и является центробежной силой. Она изменяет направление скорости, не влияя на числовое значение.

Электрон будет двигаться по окружности радиусом r с угловой частотой w_ц, которую называют циклотронной частотой. Центробежное ускорение равно силе f, деленной на массу .

Отсюда

(1)

Время одного оборота

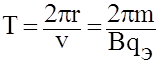
Следовательно

(2)

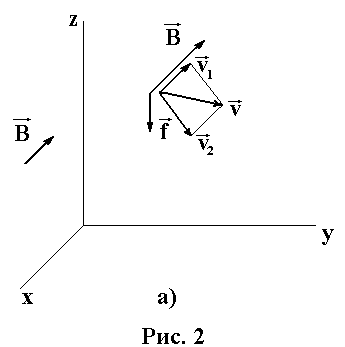
2. Движение электрона в неизменном во времени магнитном поле, когда скорость электрона не перпендикулярна силовым линиям.

Рассмотрим два случая: в первом- электрон будет двигаться в равномерном, во втором – в неравномерном поле.

а) Движение в равномерном поле. Через a на рис 2. Обозначен угол между скоростью электрона и индукцией . Разложим  на , направленную по  и численно равную , и на  , направленную перпендикулярно  и численно равную . Так как  , то наличие составляющей скорости  не вызывает силы воздействия на электрон. Движение со скоростью приводит к вращению электрона вокруг линии  подобно тому, как это было рассмотрено в первом пункте. В целом электрон будет двигатся по спирали рис. 2. б. Осевой линией которой является линия магнитной индукции. Радиус спирали  шаг спирали

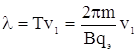(3)

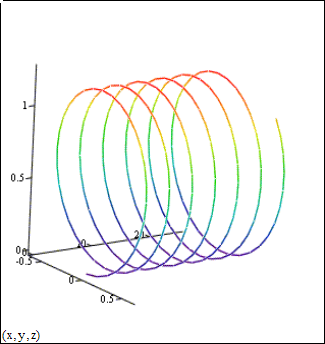Поступательное и одновременно вращательное движение иногда называют дрейфом электрона.

Рис 2. б.

б) Движение в неравномерном поле. Если магнитное поле неравномерно, например сгущается ( рис.2 в.), то при движении по спирали электрон будет попадать в точки поля, где индукция В увеличивается. Но чем больше индукция В, тем при прочих равных условиях меньше радиус спирали r. Дрейф электрона будет происходить в этом случае по спирали со всем уменьшающимся радиусом. Если бы

магнитные силовые линии образовывали расходящийся пучок, то электрон при своем движении попадал бы в точки поля со все уменьшающейся индукцией и радиус спирали возрастал бы.

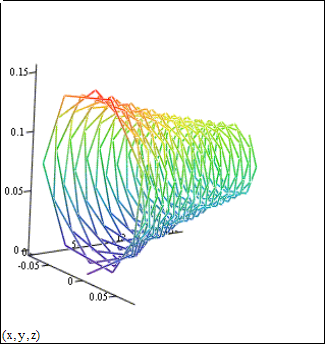
Рис 2. в.