Навигация
Фокусировка пучка электронов постоянным во времени магнитным полем (магнитная линза)
3. Фокусировка пучка электронов постоянным во времени магнитным полем (магнитная линза).
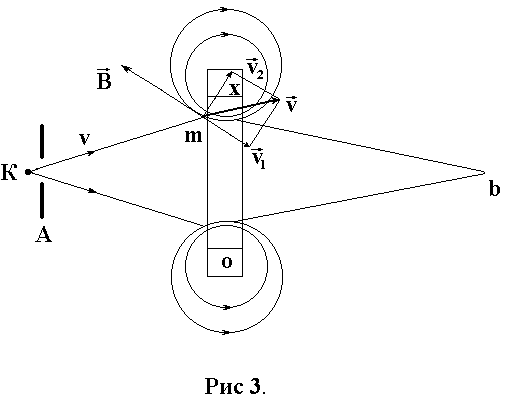
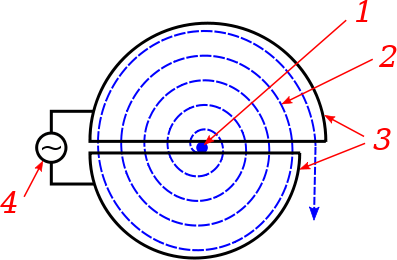
Из катода электронного прибора (рис. 3) выходит расходящийся пучок электронов. Со скоростью ![]() электроны входят в неравномерное магнитное поле узкой цилиндрической катушки с током.
электроны входят в неравномерное магнитное поле узкой цилиндрической катушки с током.
Разложим скорость электрона ![]() в произвольной точке т на две составляющие:
в произвольной точке т на две составляющие: ![]() и
и ![]() .
.
Первая ![]() направлена противоположно
направлена противоположно ![]() , а вторая
, а вторая ![]() -перпендикулярно
-перпендикулярно ![]() . Возникшая ситуация повторяет ситуацию, рассмотренную в пункте 2. Электрон начнет двигаться по спирали, осью которой является
. Возникшая ситуация повторяет ситуацию, рассмотренную в пункте 2. Электрон начнет двигаться по спирали, осью которой является ![]() . В результате электронный пучок фокусируется в точке b.
. В результате электронный пучок фокусируется в точке b.
4. Движение электронов в равномерном электрическом поле. Принцип работы электронного осциллографа.
Электрон, пройдя расстояние от катода К до узкого отверстия в аноде А (рис. 4, а), под действием ускоряющего напряжения Uак увеличивает свою кинетическую энергию на величину работы сил поля.
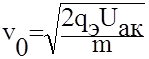 |
Скорость
![]()
При дальнейшем прямолинейном движении по оси х электрон попадает в равномерное электрическое поле, напряженностью Е между отклоняющими пластинами 1 и 2 (находятся в плоскостях, параллельных плоскости zох).
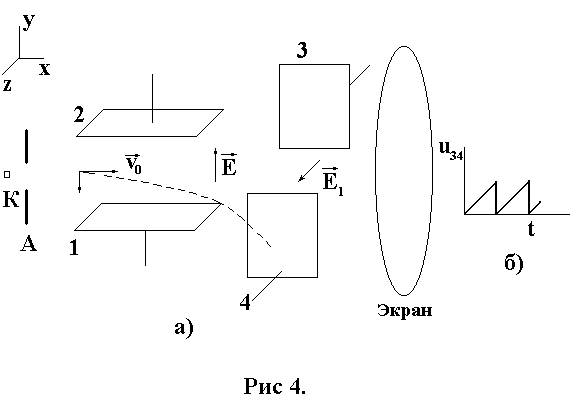 |
Напряженность Е направлена вдоль оси у. Пока электрон движется между отклоняющимися пластинами, на него действует постоянная сила Fy = —qэE. направленная но оси —у. Под действием этой силы электрон движется вниз равноускоренно, сохраняя постоянную скорость
5. Фокусировка пучка электронов постоянным во времени электрическим полем (электрическая линза).
Фокусировка основана на том что, проходя через участок неравномерного электрического поля, электрон отклоняется в сторону эквипотенциали с большим значением потенциала (рис. 5, а). Электрическая линза образована катодом, испускающим электроны, анодом, куда пучок электронов приходит сфокусированным, и фокусирующей диафрагмой, представляющей собой пластинку с круглым отверстием в центре (рис. 5, б). Диафрагма имеет отрицательный потенциал по отношению к окружающим ее точкам пространства, вследствие этого эквинотенциали электрического поля как бы выпучиваются через
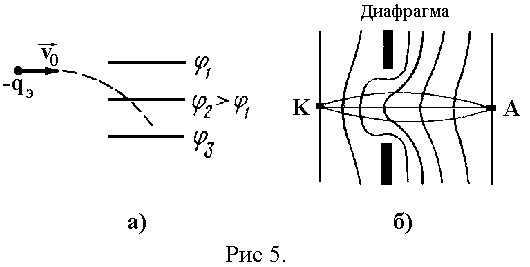 |
диафрагму по направлению к катоду. Электроны, проходя через отверстие в диафрагме и отклоняясь в сторону, фокусируются на аноде.
6. Движение электрона в равномерных, взаимно перпендикулярных, неизменных во времени магнитном и электрическом полях.
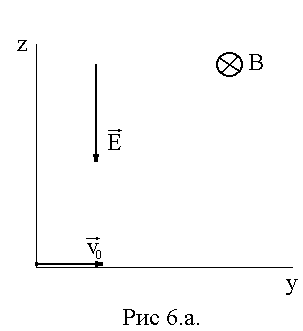 |
Пусть электрон с зарядом q= —qэ, и массой т с начальной скоростью
Уравнение движения ![]() или
или
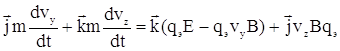
Следовательно, 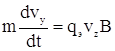 ;
; ![]()
В соответствии с формулой (2) заменим qэB/m на циклотронную частоту wц. Тогда
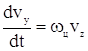 (4)
(4)
![]() (5)
(5)
Продифференцируем (4) по t и в правую часть уравнения подставим (5).
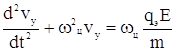 (6)
(6)
Решим уравнение классическим методом: vy=vy пр+vy св:
![]()
![]()
Составим два уравнения для определения постоянных интегрирования.
Так как при t=0 vy=v, то ![]() . При t=0 vz=0. Поэтому
. При t=0 vz=0. Поэтому ![]() или
или![]() . Отсюда
. Отсюда ![]() и
и ![]() .
.
Таким образом, 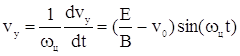
Пути, пройденные электроном по осям у и z:
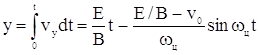
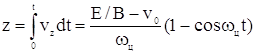
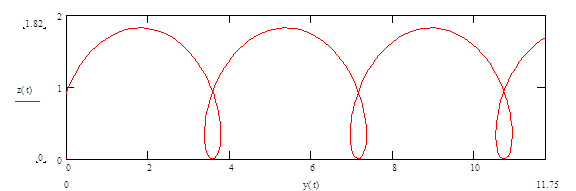
На рис. 6, б, в, г изображены три характерных случая движения при различных значениях v0. На рис. 6, б трохоида при v0=0, максимальное отклонение по оси z равно ![]() .
.
Если v0>0 и направлена по оси +y, то траекторией является растянутая
трохоида (рис. 6, в) с максимальным отклонением 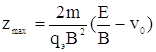 .
.
Если v0<0 и направлена по оси —у, то траекторией будет сжатая трохоида (рис. 6, г) с 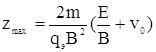 .
.
Когда магнитное и электрическое поля мало отличаются от равномерных, траектории движения электронов близки к трохоидам.
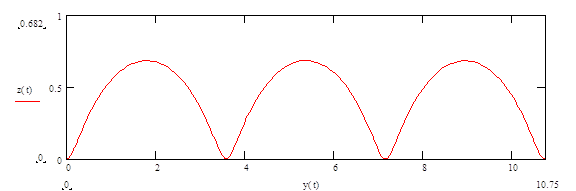 |
Рис 6.б
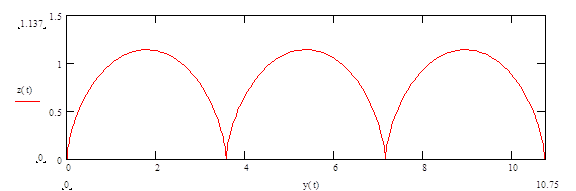 |
Рис 6.в
Рис 6.г
 |
7. Движение заряженных частиц в кольцевых ускорителях.
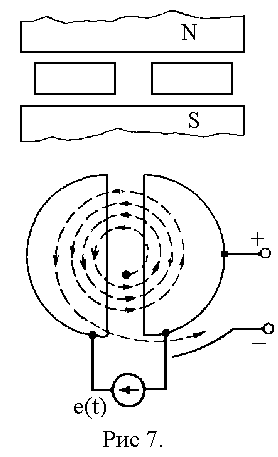 |
Циклотрон представляет собой две полые камеры в виде полуцилиндров из проводящего неферромагпитного материала. Эти камеры находятся в сильном равномерном магнитном поле индукции
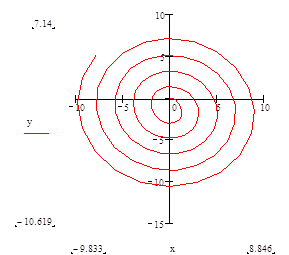 |
движение по окружности радиусом
Рис 8.
Вывод заряда из циклотрона осуществляется с помощью постоянного электрического поля, создаваемого между одной из камер (на рис. 7 правой) и вспомогательным электродом А. С увеличением скорости ![]() она становится соизмеримой со скоростью света, масса частицы т во много раз увеличивается. Возрастает и время t1, прохождения полуоборота. Поэтому одновременно с увеличением скорости частицы необходимо уменьшать либо частоту источника напряжения Umcos(wt) (фазотрон), либо величину индукции магнитного поля (синхротрон), либо частоту и индукцию (синхрофазотрон).
она становится соизмеримой со скоростью света, масса частицы т во много раз увеличивается. Возрастает и время t1, прохождения полуоборота. Поэтому одновременно с увеличением скорости частицы необходимо уменьшать либо частоту источника напряжения Umcos(wt) (фазотрон), либо величину индукции магнитного поля (синхротрон), либо частоту и индукцию (синхрофазотрон).
Похожие работы
... , разрезал его вдоль оси и раздвинул половинки (их сейчас называют дуантами). Эту разрезанную банку надо вложить между полюсами электромагнита, а в ее центре поместить источник не особенно быстрых заряженных частиц, подчиняющихся законам ньютоновской механики. В постоянном магнитном поле они станут закручиваться и двигаться по инерции по окружностям фиксированного радиуса (разумеется, в камере ...
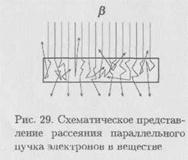
... свободных уровней электронами. При движении быстрых бета - частиц через поглощающую среду существенную роль играют потери на излучение. Взаимодействие бета - частиц с кулоновским полем атомных ядер приводит к торможению бета - частиц с испусканием тормозного излучения. В соответствии с классической электродинамикой заряд, испытывающий ускорение a, излучает энергию где e - заряд частицы, c - ...
... гамма-фотонов через вещество.» Курс физики. И.В.Савельев. 1989. Т.3. С.277. «... замкнутые токи и связанные с ними магнитные моменты.» Физическая энциклопедия. МАГНЕТИЗМ МИКРОЧАСТИЦ. Элементарные частицы обладают физическими свойствами, по которым можно судить об их строении. Устойчивые замкнутые токи можно экспериментально наблюдать, например, в сверхпроводниках, где токи проводимости ...
... на значения функции H. N_[N] Массив, в котором мы храним длины массивов. Функция main i Временные переменные. Счетчики. l j e Заряд частицы. С её помощью вычисляется H. v Скорость частицы. С её помощью вычисляется H. H Напряженность поля движущейся частицы. alfa Угол между направлением скорости и прямой, проведенной от частицы в данную точку поля.α=∏/2 t Время. res ...



0 комментариев