Кинетика двухатомного газа

 

«Кинетика двухатомного газа».Интересный курсовик по физике (копия с книги). «Автор» Степанов Евгений. ЭТ-9-00 МЭИ. Написан в 2002 . Зачтён с отметкой отл. на каф. физики имени Фабриканта. Обратите внимание на размер шрифта и отступы …. Лучше так не делайте. См. список литературы в конце.

План:

1. Введение

2. Двухатомный газ с молекулами из различных атомов. Вращение молекул.

3. Двухатомный газ. Колебания атомов.

4. Двухатомный газ.

 Влияние электронного момента.

5. Литература

1.Введение.

Простейшими молекулами газа являются двухатомные молекулы (частный случай идеального газа), представляющие устойчивое соединение двух различных атомов. Мы лишены возможности подробно разбирать вопрос о природе сил, приводящих к образованию молекул из свободных атомов, а также детально описывать движение атомов в молекулах. Поэтому мы ограничимся лишь поверхностной характеристикой молекул, приведя только те сведения, которые нам понадобятся для описания двухатомного газа (вращение молекул одинаковых и различных атомов, колебания атомов, влияние электронного момента).

2. Двухатомный газ с молекулами из различных атомов. Вращение молекул

Переходя к вычислению термодинамических величин двухатомного газа, прежде всего, укажем, что подобно тому, как одноатомные газы имеет смысл рассматривать лишь при температурах Т, малых по сравнению с энергией ионизации, двухатомный газ можно рассматривать как таковой лишь при условии малости Т по сравнению с энергией диссоциации молекулы. Это обстоятельство, в свою очередь приводит к тому, что в статистической сумме надо учитывать лишь нормальный электронный терм молекулы.

Мы начнем с изучения наиболее важного случая, когда в своем нормальном электронном состоянии молекула газа не имеет ни спина, ни орбитального момента вращения относительно оси (S=О, Λ=0);

такой электронный терм не обладает, конечно, тонкой структурой. Кроме того, следует различать случаи молекул, составленных из различных атомов (в том числе различных изотопов одного и того же элемента), и молекул, состоящих из одинаковых атомов, ибо последний случай обладает некоторыми специфическими особенностями. Мы будем считать, что молекула состоит из различных атомов.

Как известно, уровень энергии двухатомной молекулы складывается в известном приближении из трех независимых частей—электронной энергии (в которую включают также и энергию кулонового взаимодействия ядер в их равновесном положении и которую мы будем отсчитывать от суммы энергий разведенных атомов), вращательной энергии и энергии колебаний ядер внутри молекулы. Для синглетного электронного терма эти уровни могут быть написаны в виде:

(1)

 

 

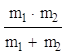Здесь —электронная энергия, ћω—колебательный квант, v—коле-бательное квантовое число, K—вращательное квантовое число (мо-мент вращения молекулы, I= m' —момент инерции молекулы (m'= приведенная масса обоих атомов, —равновесное

значение расстояния между ядрами).

При подстановке выражения (1) в статистическую сумму последняя распадается, очевидно, на три независимых множителя:

(2)

где «вращательная» и «колебательная» суммы определяются как

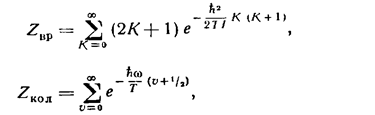
(3)

(4)

 

причем множитель учитывает вырождение

вращательных уровней по направлениям момента К. Соответственно, свободная энергия представится в виде суммы трех частей:

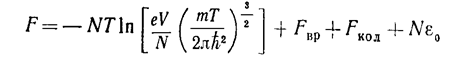
(5)

m= — масса молекулы). Первый член можно назвать поступательной частью Fпос (поскольку он связан со степенями свободы поступательного движения молекул), а

(6)

 

—вращательной и колебательной частями. Поступательная часть всегда выражается формулой типа (43,1)1 с постоянной теплоемкостью Спос=3/2 и химической постоянной:

 

(7)

Полная теплоемкость газа запишется в виде суммы нескольких членов:

(8)

каждый из которых связан с тепловым возбуждением соответственно поступательного движения молекулы, ее вращения и колебаний атомов внутри молекулы.

Займемся вычислением свободной вращательной энергии. Если температура настолько высока, что

(«вращательный квант» ћ²/2I мал по сравнению с T)1), то в сумме (3) основную роль играют члены с большими К. Но при больших значениях К вращение молекулы квазиклассично. Поэтому в этом случае статистическая сумма Zвр может быть заменена соответствующим классическим интегралом:

(9)

где ε(М)—классическое выражение кинетической энергии вращения как функции момента вращения М. Вводя связанную с молекулой вращающуюся систему координат ξ, η, ζ, с осью ζ, вдоль оси молекулы и, имея в виду то, что двухатомная молекула обладает двумя вращательными степенями свободы, а момент вращения линейной механической системы перпендикулярен к ее оси, пишем:

 

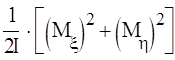
ε(M)= (10)

 

Элемент dτвр есть деленное на (2лћ)² произведение дифференциалов dMξdMη и дифференциалов соответствующих Mξ и Mη «обобщенных координат», т. е. бесконечно малых углов поворота вокруг осей

ξ и η: dφξdφη 1). Но произведение двух бесконечно малых углов поворота вокруг осей ξ и η есть не что иное, как элемент телесного угла d0ζ для направления третьей оси ζ; интегрирование по телесному углу даст 4π. Таким образом, имеем 2):

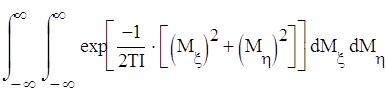
Zвр =4π/(2πћ)²  =

=2IT/ћ²

Отсюда свободная энергия

Fвр =-NTlnT-NTln2I/ћ² (10)

 

Таким образом, при рассматриваемых не слишком низких температурах вращательная часть теплоемкости оказывается постоянной и равной Cвр =1 в соответствии с общими результатами классического рассмотрения идеального газа (по ½ на каждую вращательную степень свободы). Вращательная часть химической постоянной равна ξвр =ln(2I/ћ²). Мы увидим ниже, что существует значительная область температур, в которой выполнено условие T>>ћ²/2I и в то же время колебательная часть свободной энергии, а с нею и колебательная часть теплоемкости отсутствуют. В этой области теплоемкость двухатомного газа равна Cν=Cпос+Cвр , т.е.

 

 Cν =5/2, Сp =7/2, (11)

а химическая постоянная ξ= ξпос+ ξвр:

(12)

В обратном предельном случае низких температур

T<<ћ²/2I

достаточно сохранить два первых члена суммы:

Zвр=1+3exp(-ћ²/IT),

и для свободной энергии получим в том же приближении:

Fвр=-3NTexp(-ћ²/IT). (13)

Отсюда энтропия

Sвр=3N ћ²/(IT)[exp(-ћ²/IT)](1+ IT/ ћ²) (14)

и теплоемкость

Свр=3N(ћ²/IT) ² exp(-ћ²/IT). (15)

Таким образом, вращательные энтропия и теплоемкость газа при T→0 обращаются в нуль в основном по экспоненциальному закону. При низких температурах,

Следовательно, двухатомный

газ ведет себя как одноатомный; Cвр как его теплоемкость, так и  химическая постоянная имеют те же значения, которые имел бы одноатомный газ с части- цами массы m.

В общем случае произвольных 2IT/ ћ²

температур сумма Zвр должна

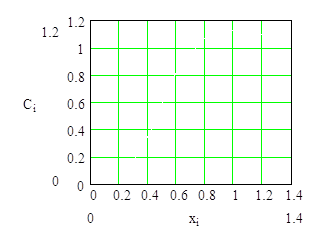
вычисляться численно. На рис. 1

приведен график Свр как функции

от 2IT/ ћ². Вращательная теплоемкость Рис. 1.

имеет максимум, равный 1.1 при T=0.81(ћ²/2I),

после чего асимптотически приближается к классическому значению 1 1).