Навигация
Двухатомный газ. Колебания атомов
3. Двухатомный газ. Колебания атомов.
Колебательная часть термодинамических величин газа становится существенной при значительно более высоких температурах, чем вращательная, потому что интервалы колебательной структуры термов велики по сравнению с интервалами вращательной структуры 1).
Мы будем считать, однако, температуру большой лишь настолько, чтобы были возбуждены в основном не слишком высокие колебательные уровни. Тогда колебания являются малыми (а потому и гармоническими), и уровни энергии определяются обычным выражением
Ћω(v+1/2) использованным в (4).
Вычисление колебательной статистической суммы Zкол (4) производится элементарно. Вследствие очень быстрой сходимости ряда суммирование можно формально распространить до v = оо. Условимся
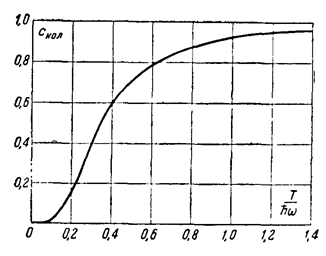
Рис. 2.
отсчитывать энергию молекулы от наиболее низкого (v=0) колебательного уровня (т. е. включаем ћω/2 в постоянную ε0 в (1)).
Тогда имеем:
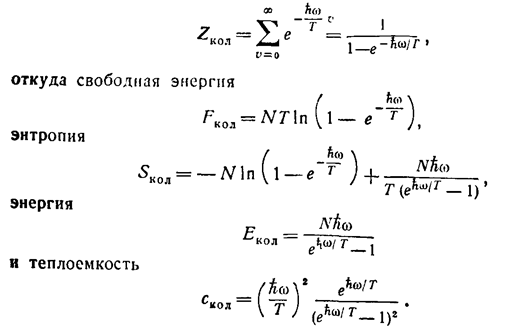
(21)
(22)
(23)
(24)
На рис. 2 изображен график зависимости Скол от T/ћω.
При низких температурах (ћω>>T) все эти величины стремятся экспоненциально к нулю:
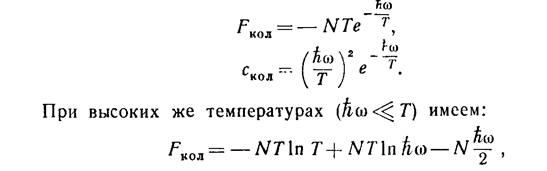
(25)
(26)
чему соответствует постоянная теплоемкость Скол=1 1) и химическая постоянная ξкол=-lnћω. Складывая со значениями (11), (12), найдем, что при температурах T>>ћω полная теплоемкость двухатомного газа равна 2)
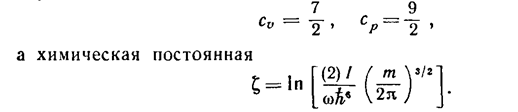
(27)
(28)
В этой формуле для молекул из одинаковых атомов множитель [(2)] должен быть опущен. Первые два члена разложения Eкол равны
![]()
(29)
Появление здесь постоянного члена — 1/2Nћω связано с тем, что, мы отсчитываем энергию от низшего квантового уровня (т. е. от энергии «нулевых колебаний»), между тем как классическая энергия должна была бы отсчитываться от минимума потенциальной энергии.
Выражение (26) для свободной энергии можно, конечно, получить и классическим путем, поскольку при T>>ћω существенны большие квантовые числа V, для которых движение квазиклассично. Классическая энергия малых колебаний с частотой ω имеет вид
![]()
(т'—приведенная масса). Интегрирование с этим выражением для ε даст для статистического интеграла значение
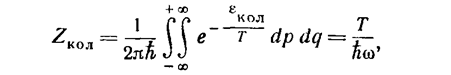
(30)
соответствующее (26) 1) (ввиду быстрой сходимости интеграла интегрирование по dq можно вести в пределах от -∞ до +∞).
При достаточно высоких температурах, когда возбуждены колебания с большими v, могут стать существенными эффекты ангармоничности колебаний и взаимодействия колебаний с вращением молекулы (эти эффекты, принципиально, одного порядка). Благодаря тому, что v велико, соответствующая поправка к термодинамическим величинам может быть определена классическим путем.
Рассмотрим молекулу как механическую систему двух частиц, взаимодействующих по закону U(r), в системе координат, в которой покоится их центр инерции. Энергия (функция Гамильтона), описывающая классически точным образом вращение и колебания системы, есть сумма кинетической энергии (как энергии частицы с приведенной массой т' ) и потенциальной энергии U(r). Статистический интеграл после интегрирования по импульсам сводится к интегралу по координатам:
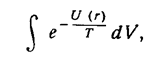
а после интегрирования по углам (в сферических координатах) остается интеграл
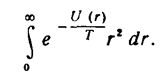
Приближение, соответствующее независимым гармоническим колебаниям и вращению молекулы, получается, если положить U(r)=U0+1/2m′ω²(r-r0)², и при интегрировании заменить медленно меняющийся множитель r² на г02, где r0—равновесное расстояние между обеими частицами; U0=U(r0). Чтобы учесть ангармоничность колебаний и их взаимодействие с вращением, пишем теперь
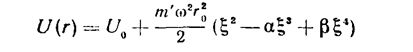
(31)
( ξ= (r/r0)—1, α и β — постоянные) и затем разлагаем все подин-тегральное выражение, выделив из него множитель
![]()
по степеням ξ. В разложении надо сохранить члены, дающие после интегрирования лишь первую после основной степень температуры; интегрирование по dξ, производится в пределах от -∞ до +∞.
Нулевой член разложения дает обычное значение статистического интеграла, а все остальные — искомую поправку. Опуская промежуточные вычисления, приведем окончательный результат для поправки к свободной энергии:
![]()
(32)
Таким образом, эффекты ангармоничности колебаний (и их взаимодействия с вращением) приводят к поправке в свободной энергии, пропорциональной квадрату температуры. Соответственно, к теплоемкости прибавляется член, пропорциональный первой степени температуры.
4. Двухатомный газ. Влияние электронного момента.
Некоторые (правда, весьма немногочисленные) молекулы обладают в своем нормальном электронном состоянии отличным от нуля орбитальным моментом или спином.
Существование отличного от нуля орбитального момента Λ приводит, как известно, к двукратному вырождению электронного терма, соответственно двум возможным направлениям этого момента относительно оси молекулы 1). Это обстоятельство отразится на термодинамических величинах газа в том отношении, что благодаря удвоению статистической суммы к химической постоянной добавится величина
![]()
(33)
Наличие не равного нулю спина S приводит к расщеплению на 2S+1 термов; интервалы этой тонкой структуры, однако, настолько ничтожны (при Λ=0), что при вычислении термодинамических величин ими можно всегда пренебречь. Наличие спина приводит лишь к увеличению кратности вырождения всех уровней в (2S+1) раз, соответственно чему к химической постоянной добавится величина
![]()
(34)
Особого рассмотрения требует тонкая структура, возникающая при S≠0, Λ≠0 . Интервалы тонкой структуры при этом могут достигать значений, делающих необходимым их учет при вычислении термодинамических величин. Выведем формулы для случая дублетного электронного терма 2).
Каждая компонента электронного дублета имеет свою колебательную и вращательную структуру, параметры которой для обеих компонент можно считать одинаковыми. Поэтому в статистической сумме (2) появится еще один множитель:
![]()
где g0,g1,—кратности вырождения компонент дублета, Δ—расстояние между ними. К свободной энергии соответственно прибавится «электронная» часть, равная
![]() (35)
(35)
Выпишем также «электронную» теплоемкость, которая должна быть добавлена к остальным частям теплоемкости:
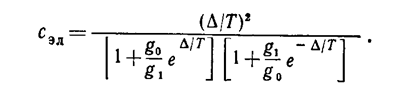
(36)
В обоих пределах Т→0 и Т→∞ Сэл, естественно, обращается в нуль, а при некоторой температуре Т~∆ имеет максимум.
Литература:
1. В. Г. Левич Курс Теоретической Физики .Том 1.
М. Наука. 1969
2. Л. Д. Ландау и Е. М. Лифшищ Статистическая Физика . Том 5. М. Наука. 1964
3. А. В. Митин и О. С. Зуева Введение в квантовую механику. Часть1. М. МЭИ. 1996
1 стр.151, Л.Д.Ландау, Е.М.Лифшиц: “Статистическая физика”.:1964 г.
1 Фактически это условие всегда выполняется для всех газов, за исключением обоих изотопов водорода. Для примера укажем значения ћ²/2kI для некоторых молекул: Н2:85,4°; D2:43°; HD:64°; N2:2,9°; O2:2,1°; Сl2:0,36˚; N0:2,4°; HCI:15,2°.
1 Необходимо иметь в виду, что такой способ написания в известном смысле условлен, так как dφξ и dφη не являются полными дифференциалами какой бы то ни было функции положения осей.
2 Это значение Zвр можно получить также и иным способом: считая числа К в сумме (3) большими и заменяя суммирование интегрированием по К, найдем:
Zвр ≈
1 Можно получить асимптотическое разложение термодинамических величин при больших значениях 2TI/ ћ². Для теплоемкости первые два члена разложения равны: Свр=1+1/45(ћ²/2TI)². Это разложение дает плохое приближение к функции Свр(T).
1 Для примера укажем значения ћω/k для некоторых двухатомных газов: Н2: 6100°; N2: 3340°; О2: 2230°; NO: 2690°; НСl: 4140°.
1 В соответствии с классическими результатами.
2 Как видно из рис. 2, Скол в действительности приближается к своему предельному значению 1 уже при Т≈ ћω (так, при T/ћω=1: Скол==0,93). Практическое условие применимости классических выражений можно написать как Т >> ћω/3.
1 Это же значение получается путем замены суммирования по v интегрированием по dv.
1 Строго говоря, происходит расщепление терма на два уровня (так называемое Λ-удвоение), расстояние между которыми, однако, настолько ничтожно, что им можно здесь полностью пренебречь.
2 Такой случай осуществляется у NO; нормальный электронный терм молекулы NO есть дублет П1/2,3/2, с шириной, равной (в градусах) ∆=178°. Обе компоненты дублета двукратно вырождены.
Похожие работы
... долей) исходных веществ. ► Стехиометрия – раздел химии, в котором рассматриваются массовые или объемные отношения между реагирующими веществами. Законы стехиометрии так же непреложны, как и любые другие естественнонаучные законы; кроме того, их знание очень полезно для прикладной химии, потому что позволяет количественно рассчитать выход химической реакции и необходимое количество исходных ...
... , т. е. к увеличению скорости реакции. Количественно зависимость между скоростью реакции и молярными концентрациями реагирующих веществ описывается основным законом химической кинетики — законом действующих масс. Скорость химической реакции при постоянной температуре прямо пропорциональна произведению концентраций реагирующих веществ. Для мономолекулярной реакции скорость реакции ...
... одним из основоположников статистической физики и физической кинетики австрийским физиком Людвигом Больцманом в 1872 году и носящее его имя. §1 Функция распределения. Для вывода кинетического уравнения Больцмана рассмотрим одноатомный идеальный газ, т.е. достаточно разряженный газ, состоящий из электрически нейтральных атомов или молекул. Единственным видом взаимодействия между частицами ...
... и отработка методов превращения последних в крезолы. Классическим методом синтеза фенолов является щелочное плавление сульфокислот ароматических углеводородов Этот метод до сих пор используют для получения фенола и β- нафтола из бензола и нафталина соответственно. Oн, по-видимому, наиболее перспективен для производства п-крезола из толуола и в этом варианте реализован в ряде стран. ...
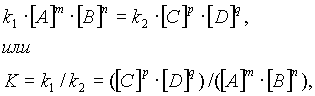
0 комментариев