Математическое моделирование в физике

1.  Математическое моделирование в физике

 

Понятие модели

Нас окружают сложные технические системы. В процессе проектирования новой или модернизации существующей технической системы решаются задачи расчета параметров и исследования процессов в этой системе. При проведении многовариантных расчетов реальную систему заменяют моделью.

Модель – это материальный или мысленно представленный объект, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.

В широком смысле модель определяют как отражение наиболее существенных свойств объекта.

Математическая модель технического объекта - совокупность математических объектов и отношений между ними, которая адекватно отражает свойства исследуемого объекта, интересующие исследователя.

Хорошо построенная модель доступнее для исследования – нежели реальный объект. Например, недопустимы эксперименты с элементарными частицами для школьников страны в познавательных целях, здесь без модели не обойтись.

Модель может быть представлена различными способами.

 инвариантная - запись соотношений модели с помощью традиционного математического языка безотносительно к методу решения уравнений модели;

аналитическая - запись модели в виде результата аналитического решения исходных уравнений модели;

алгоритмическая - запись соотношений модели и выбранного численного метода решения в форме алгоритма.

схемная (графическая) - представление модели на некотором графическом языке (например, язык графов, эквивалентные схемы, диаграммы и т.п.);

физическая

аналоговая

Наиболее универсальным является математическое описание процессов - математическое моделирование.

В понятие математического моделирования включают и процесс решения задачи на ЭВМ.

 
Обобщенная математическая модель

Математическая модель описывает зависимость между исходными данными и искомыми величинами. Элементами обобщенной математической модели являются (рис. 1):

множество входных данных (переменные) X,Y;
X - совокупность варьируемых переменных; Y - независимые переменные (константы);

математический оператор L, определяющий операции над этими данными; под которым понимается полная система математических операций, описывающих численные или логические соотношения между множествами входных и выходных данных (переменные);

множество выходных данных (переменных) G(X,Y); представляет собой совокупность критериальных функций, включающую (при необходимости) целевую функцию.

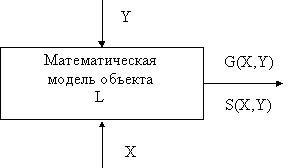
Рис. 1.

Математическая модель является математическим аналогом проектируемого объекта. Степень адекватности ее объекту определяется постановкой и корректностью решений задачи проектирования. Множество варьируемых параметров (переменных) X образует пространство варьируемых параметров R_x (пространство поиска), которое является метрическим с размерностью n, равной числу варьируемых параметров. Множество независимых переменных Y образуют метрическое пространство входных данных R_y. В том случае, когда каждый компонент пространства R_y задается диапазоном возможных значений, множество независимых переменных отображается некоторым ограниченным подпространством пространства R_y. Множество независимых переменных Y определяет среду функционирования объекта, т.е. внешние условия, в которых будет работать проектируемый объект.

Это могут быть:

- технические параметры объекта, не подлежащие изменению в процессе проектирования;
- физические возмущения среды, с которой взаимодействует объект проектирования;
- тактические параметры, которые должен достигать объект проектирования.

Выходные данные рассматриваемой обобщенной модели образуют метрическое пространство критериальных показателей R_G.

 Схема использования математической модели в системе автоматизированного проектирования показана на рис.2.

 

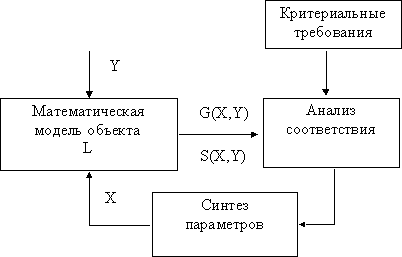
Рис. 2.

Основными требованиями, предъявляемыми к математическим моделям, являются требования адекватности, универсальности и экономичности.

Адекватность. Модель считается адекватной, если отражает заданные свойства с приемлемой точностью. Точность определяется как степень совпадения значений выходных параметров модели и объекта.
Точность модели различна в разных условиях функционирования объекта. Эти условия характеризуются внешними параметрами. В пространстве внешних параметров выделить область адекватности модели, где погрешность меньше заданной предельно допустимой погрешности. Определение области адекватности моделей - сложная процедура, требующая больших вычислительных затрат, которые быстро растут с увеличением размерности пространства внешних параметров. Эта задача по объему может значительно превосходить задачу параметрической оптимизации самой модели, поэтому для вновь проектируемых объектов может не решаться.

Универсальность - определяется в основном числом и составом учитываемых в модели внешних и выходных параметров.

Экономичность модели характеризуется затратами вычислительных ресурсов для ее реализации - затратами машинного времени и памяти.

Противоречивость требований к модели обладать широкой областью адекватности, высокой степени универсальности и высокой экономичности обусловливает использование ряда моделей для объектов одного и того же типа.

Методы получения моделей

 

Получение моделей в общем случае - процедура неформализованная. Основные решения, касающиеся выбора вида математических соотношений, характера используемых переменных и параметров, принимает проектировщик. В тоже время такие операции, как расчет численных значений параметров модели, определение областей адекватности и другие, алгоритмизированы и решаются на ЭВМ. Поэтому моделирование элементов проектируемой системы обычно выполняется специалистами конкретных технических областей с помощью традиционных экспериментальных исследований. Методы получения функциональных моделей элементов делят на теоретические и экспериментальные. Теоретические методы основаны на изучении физических закономерностей протекающих в объекте процессов, определении соответствующего этим закономерностям математического описания, обосновании и принятии упрощающих предположений, выполнении необходимых выкладок и приведении результата к принятой форме представления модели. Экспериментальные методы основаны на использовании внешних проявлений свойств объекта, фиксируемых во время эксплуатации однотипных объектов или при проведении целенаправленных экспериментов. Каким образом происходит построение математической модели?

Во–первых, формулируется цель и предмет исследования.

Во–вторых, выделяются наиболее важные характеристики, соответствующие данной цели.

В–третьих, словесно описываются взаимосвязи между элементами модели.

Далее взаимосвязь формализуется.

И производится расчет по математической модели и анализ полученного решения.

Используя данный алгоритм можно решить любую оптимизационную задачу, в том числе и многокритериальную, т.е. ту в которой преследуется не одна, а несколько целей, в том числе противоречивых. Оптимизационные модели, в том числе многокритериальные, имеют общее свойство– известна цель(или несколько целей) для достижения которой часто приходится иметь дело со сложными системами, где речь идет не столько о решении оптимизационных задач, сколько об исследовании и прогнозировании состояний в зависимости от избираемых стратегий управления. И здесь мы сталкиваемся с трудностями реализации прежнего плана. Они состоят в следующем:

сложная система содержит много связей между элементами

реальная система подвергается влиянию случайных факторов, учет их аналитическим путем невозможен

возможность сопоставления оригинала с моделью существует лишь в начале и после применения математического аппарата, т.к. промежуточные результаты могут не иметь аналогов в реальной системе.

В связи с перечисленными трудностями, возникающими при изучении сложных систем, практика потребовала более гибкий метод, и он появился – имитационное моделирование "Simujation modeling". Обычно под имитационной моделью понимается комплекс программ для ЭВМ, описывающий функционирование отдельных блоков систем и правил взаимодействия между ними. Использование случайных величин делает необходимым многократное проведение экспериментов с имитационной системой (на ЭВМ) и последующий статистический анализ полученных результатов. Таким образом, работа с имитационной системой представляет собой эксперимент, осуществляемый на ЭВМ. В чем же заключаются преимущества?

–Большая близость к реальной системе, чем у математических моделей;

–Блочный принцип дает возможность верифицировать каждый блок до его включения в общую систему;

–Использование зависимостей более сложного характера, не описываемых простыми математическими соотношениями.

Перечисленные достоинства определяют недостатки

–построить имитационную модель дольше, труднее и дороже;

–для работы с имитационной системой необходимо наличие подходящей по классу ЭВМ;

–взаимодействие пользователя и имитационной модели (интерфейс) должно быть не слишком сложным, удобным и хорошо известным;

–построение имитационной модели требует более глубокого изучения реального процесса, нежели математическое моделирование.

Встает вопрос: может ли имитационное моделирование заменить методы оптимизации? Нет, но удобно дополняет их. Имитационная модель – это программа, реализующая некоторый алгоритм, для оптимизации управления которым прежде решается оптимизационная задача.

Итак, ни ЭВМ, ни математическая модель, ни алгоритм для ее исследования порознь не могут решить достаточно сложную задачу. Но вместе они представляют ту силу, которая позволяет познавать окружающий мир, управлять им в интересах человека.

Вычислительная мощность современных компьютеров в сочетании с предоставлением пользователю всех ресурсов системы, возможностью диалогового режима при решении задачи и анализе результатов позволяют свести к минимуму время решения задачи.

При составлении математической модели от исследователя требуется:

изучить свойства исследуемого объекта;

умение отделить главные свойства объекта от второстепенных;

оценить принятые допущения.

Что положительного в любой модели? Она позволяет получить новые знания об объекте, но, к сожалению, в той или иной степени не полна.

Модель описывает зависимость между исходными данными и искомыми величинами. Последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к искомым величинам, называют алгоритмом.

2.  Историческое развитие моделей элементарных частиц 2.1 Три этапа в развитии физики элементарных частиц

Этап первый. От электрона до позитрона: 1897-1932гг (Элементарные частицы - "атомы Демокрита" на более глубоком уровне)

Когда греческий философ Демокрит назвал простейшие, нерасчленимые далее частицы атомами, то ему все представлялось в принципе не очень сложным. Различные предметы, растения, животные построены из неделимых, неизменных частиц. Превращения, наблюдаемые в мире, - это простая перестановка атомов. Все в мире течет, все изменяется, кроме самих атомов, которые остаются неизменными.

Но в конце XIX века было открыто сложное строение атомов и был выделен электрон как составная часть атома. Затем, уже в XX веке, были открыты протон и нейтрон - частицы, входящие в состав атомного ядра. Поначалу на все эти частицы смотрели точь-в-точь, как Демокрит смотрел на атомы: их считали неделимыми и неименными первоначальными сущностями, основными кирпичиками мироздания.

Этап второй. От позитрона до кварков: 1932-1970гг (Все элементарные частицы превращаются друг в друга)

Однако ситуация привлекательной ясности длилась недолго. Все оказалось намного сложнее: как выяснилось, неизменных частиц нет совсем. В самом слове элементарная частица заключается двоякий смысл. С одной стороны, элементарный - это само собой разумеющийся, простейший. С другой стороны, под элементарным понимается нечто фундаментальное, лежащее в основе вещей.

Считать известные сейчас элементарные частицы подобными неизменными атомам Демокрита мешает следующий простой факт. Ни одна из частиц не бессмертна. Большинство частиц, называемых сейчас элементарными, не могут прожить более двух миллионов долей секунды, даже в отсутствие какой-либо воздействие извне. Свободный нейтрон (нейтрон, находящийся вне атомного ядра) живет в среднем 15 минут.

Лишь фотон, электрон, протон и нейтрино сохраняли бы свою неизменность, если бы каждая из них была одна в целом мире.

Но у электронов и протонов имеются опаснейшие собратья - позитроны и антипротоны, при столкновении с которыми происходит взаимное уничтожение этих частиц и образование новых.

Фотон, испущенный настольной лампой, живет не более 10^-8с. Это то время, которое ему нужно, чтобы достичь страницы книги и поглотиться бумагой.

Лишь нейтрино почти бессмертно из-за того, что оно чрезвычайно слабо взаимодействует с другими частицами, хотя такие столкновения случаются крайне редко.

Итак, в извечном стремлении к отысканию неизменного в нашем изменчивом мире ученые оказались не на "гранитном основании", а на "зыбком песке".

Все элементарные частицы превращаются друг в друга, и эти взаимные превращения - главный факт их существования.

Представления о неизменности элементарных частиц оказались несостоятельными. Но идея об их неразложимости сохранилась.

Элементарные частицы уже далее неделимы, но они неисчерпаемы по своим свойствам. Вот что заставляет так думать. Пусть у вас возникло естественное желание исследовать, состоит ли, например, электрон из каких-либо других субэлементарных частиц. Что нужно сделать для того, чтобы попытаться расчленить электрон? Можно придумать только один способ. Это тот же способ, к которому прибегает ребенок, если хочет узнать, что находится внутри пластмассовой игрушки, - сильный удар.

Разумеется, по электрону нельзя ударить молотком. Для этого можно воспользоваться другим электроном, летящим с огромной скоростью, или какой-либо иной, движущейся с большой скоростью элементарной частицей.

Современные ускорители сообщают заряженными частицами скорости, очень близкие к скорости света.

Что же происходит при столкновении частиц сверхвысокой энергии? Они отнюдь не дробятся на нечто такое, что можно было бы назвать их составными частями. Нет, они рождают новые частицы из числа тех, которые уже фигурируют в списке элементарных частиц. Чем больше энергия сталкивающихся частиц, тем большее количество и притом более тяжелых частиц рождается. Это возможно благодаря тому, что при увеличении скорости масса частиц растет. Всего лишь из одной пары любых частиц с возросшей массой можно в принципе получить все известные на сегодняшний день частицы.

Возможно, что при столкновении частиц с недоступной пока нам энергией будут рождаться и какие-то новые, еще неизвестные частицы. Но сути дела это не изменит. Рождаемые при столкновениях новые частицы никак нельзя рассматривать как составные части частиц - "родителей". Ведь "дочерние" частицы, если их ускорить, могут, не изменив своей природы, а только увеличив массу, породить в свою очередь при столкновениях сразу несколько таких же в точности частиц, какими были их "родители", да еще и множество других частиц.

Итак, по современным представлениям элементарные частицы - это первичные, неразложимые далее частицы, из которых построена вся материя. Однако неделимость элементарных частиц не означает, что у них отсутствует внутренняя структура.

Этап третий. От гипотезы о кварках (1964г) до наших дней. (Большинство элементарных частиц имеет сложную структуру)

В 60-е годы возникли сомнения в том, что все частицы, называемые сейчас элементарными, полностью оправдывают это название. Основание для сомнений простое: этих частиц очень много.

Открытие элементарной частицы всегда составляла и сейчас составляет выдающийся триумф науки. Но уже довольно давно к каждому очередному триумфу начала примешиваться доля беспокойства. Триумфы стали следовать буквально друг за другом. Были открыта группа так называемых "странных" частиц: К-мезонов и гиперонов с массами, превышающими массу нуклонов. В 70-е годы к ним прибавилась большая группа "очарованных" частиц с еще большими массами. Кроме того, были открыты короткоживущие частицы с временем жизни порядка 10^-22-10^-23 с. Эти частицы были названы резонансами, и их число перевалило за двести.

Вот тогда-то в 1964г М. Гелл-Манном и Дж. Цвейгом была предложена модель, согласно которой все частицы, участвующие в сильных взаимодействиях, построены из более фундаментальных частиц - кварков.

В настоящее время в реальности кварков почти никто не сомневается, хотя в свободном состоянии они не обнаружены.