Электрический дипольный момент

Математическое моделирование в физике Первые модели элементарных частиц Элементарные частицы и фундаментальные взаимодействия Современная модель нейтрона Электрический дипольный момент Существование кварков Практическая часть

101982

знака

таблиц

изображений

Современная модель нейтрона Читать далее: Существование кварков

2.5 Электрический дипольный момент

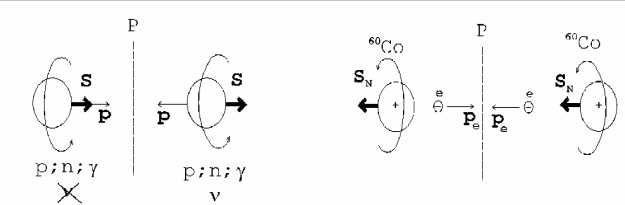
Рассмотрим движение свободного электрона, нейтрона или $\gamma$ -кванта, в котором спин частицы целиком проецируется на направление импульса, т.е. спин параллелен импульсу (рис. 5, слева). Зеркальное отражение преобразует импульс частицы и не трогает никак ориентацию спина. В зеркале мы увидим, что частица теперь движется в противоположную сторону, а "вращается" в первоначальном направлении, т.е. имеет отрицательную проекцию спина на направление импульса. Такое зеркально симметричное движение возможно как раз благодаря P-инвариантности законов распространения указанных свободных частиц. А поскольку электромагнитные взаимодействия между заряженными частицами осуществляются посредством обмена фотонами, то и любые электромагнитные процессы инвариантны относительно операции отражения в зеркале.

Рис 5

Cлева - Зеркальная симметрия свободно распространяющихся протона, нейтрона и фотона. Свободное нейтрино демонстрирует нарушение зеркальной инвариантности, поскольку нейтрино с положительной проекцией спина в природе не существует. Штриховая вертикаль символизирует зеркало. Cправа – Зеркально-неинвариантный $\beta$ -распад ⁶⁰Co.

Примером зеркально-неинвариантного процесса служит распространение нейтрино: в нашем мире, насколько мы знаем сегодня, не встречается нейтрино, спин которого параллелен импульсу. Впервые нарушение P-инвариантности, или, как чаще говорят, несохранение четности, было обнаружено при изучении $\beta$ -распада спин-поляризованных ядер ⁶⁰Co группой Ц. Ву, которая осуществила эксперимент, предложенный Ц. Ли и Ч. Янгом в 1956 г. Оказалось, что электроны предпочитают вылетать в направлении, противоположном направлению ядерного спина (рис. 5 справа). Однако симметрия все-таки может иметь место, но только относительно одновременного с зеркальным отражением перехода от частиц к античастицам. При таком преобразовании нейтрино с импульсом, направленным против спина, перейдет в реально существующее антинейтрино, спин которого параллелен импульсу. Это преобразование носит название "комбинированная инверсия" (СР). Гипотеза о возможной симметрии законов природы относительно операции СР была высказана Л.Д. Ландау. Тогда же им было замечено, что наличие электрического дипольного момента элементарной частицы требует одновременного нарушения как пространственной (Р), так и временной (Т), а следовательно, и СР-инвариантности.

Электрический дипольный момент у нейтрона, отражает неравномерное распределение заряда по объему частицы - смещение центра распределения положительного заряда относительно центра отрицательного. Представим нейтрон упрощенно в виде двух эксцентрических шариков с противоположными зарядами $\pm e$ (e - заряд электрона). Пусть d - вектор, соединяющий центры шариков и направленный от положительного заряда к отрицательному. По определению, ЭДМ - вектор $D=e \cdot d$ . Наличие присущего нейтрону выделенного направления, связанного со спином S, навязывает это направление и вектору D, который, следовательно, должен быть параллелен либо антипараллелен вектору спина. Однако между этими векторами есть существенное различие: вектор D - полярный, а S - аксиальный. Это значит, что при изменении знака всех пространственных координат вектор D переходит в - D, вектор же S никак не меняется.

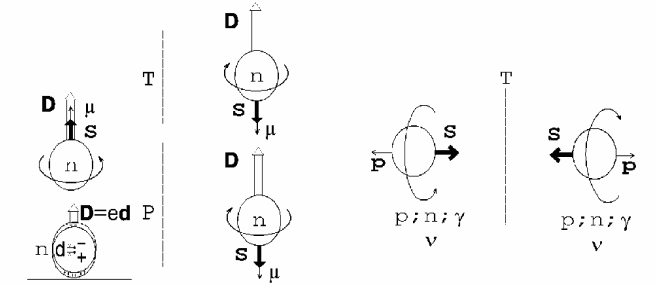
Рис 6

Слева - ЭДМ нейтрона, нарушающий пространственную и временную симметрии. Наличие у нейтрона только магнитного момента оставляло бы частицу P- и T-инвариантной. Если же нейтрон обладает и ЭДМ D, то частица в зеркальном и в обращенном во времени мире не эквивалентна исходной. Справа - T-инвариантные процессы распространения нейтрона, протона, фотона и нейтрино. При обращении движения одновременно изменяют знаки как импульс частицы, так и ее спин, поэтому частица со спином, антипараллельным импульсу, переходит в себя.

На рисунке 6 слева изображен нейтрон, полученный в результате эквивалентной операции - отражения в зеркале: здесь, наоборот, направление вектора D осталось прежним, а направление вращения изменилось на противоположное.

Аналогично и при изменении знака времени вектор D не меняется, тогда как вектор S знак меняет, поскольку направление "вращения" частицы меняется на противоположное. Другими словами, инвариантность относительно любого из этих преобразований означала бы равновероятные в противоположных направлениях ориентации вектора D, среднее значение которого из-за этого обращалось бы в нуль. Поскольку Р- инвариантность нарушается слабыми взаимодействиями и в то же время последние не нарушают Т-инвариантность (рис 6 справа), наличие ЭДМ может, с одной стороны, свидетельствовать о нарушении Т-симметрии, а с другой - о существовании какого-то, до сих пор неизвестного, взаимодействия.

В 1964 г. произошло важное событие: было непосредственно обнаружено нарушение CP-инвариантности в распаде нейтрального K-мезона на два заряженных $\pi$ -мезона. Природа этого нарушения остается загадкой до сих пор. Пока это единственный известный случай СР-нарушения. Косвенное свидетельство такого нарушения - барионная асимметрия Вселенной, т. е. тот факт, что наша Вселенная преимущественно состоит из частиц.

Хотя у нейтрона и отсутствует электрический заряд, тем не менее движущийся нейтрон взаимодействует с электрическим полем, поскольку имеет магнитный момент. Взаимодействие представляет собой релятивистский эффект, теоретическое описание которого в рамках квантовой электродинамики дал Ю. Швингер в 1948 г. Прежде всего, магнитный момент $\mu$ напрямую взаимодействует с магнитным полем напряженности H, давая основной вклад в энергию взаимодействия: $V^{\mu} = -(\mu \cdot H) = -\mu (\sigma \cdot H)$ , где $\sigma$ - единичный вектор вдоль направления спина.

Если есть электростатическое поле и незаряженная, но имеющая магнитный момент частица движется со скоростью v, то в связанной с частицей системе отсчета появляется магнитное поле $H^S = (1/c) [E \times v]$ . В результате энергия взаимодействия приобретает релятивистскую поправку, которая равна:

$V^S = - (\mu \cdot H^S) = -(1/c) (\mu \cdot [E \times v])$
Наконец, если у нейтрона есть ЭДМ, то должно появиться непосредственное взаимодействие с электрическим полем. Энергия этого взаимодействия равна

$V^D = - (D \cdot E) = - D(\sigma \cdot E)$
Прямое магнитодипольное взаимодействие нейтрона с магнитным полем вызывает прецессию вектора спина частицы вокруг вектора H., направляя электрическое поле, например, по магнитному полю или против него, мы уменьшим или увеличим угловую скорость прецессии
$\omega^{\pm} = (\mu \cdot H \pm D \cdot E)/ \hbar$ ,
Изменение угла $\Delta \varphi = (\omega^{+} - \omega^{-}) \tau = 2(D \cdot E) \tau / \hbar$ при переключении знака электрического поля непосредственно содержит информацию об ЭДМ и подлежит экспериментальному определению в методе УХН - магниторезонансном методе с использованием ультрахолодных нейтронов. Последние обладают столь низкой кинетической энергией, что полностью отражаются от стенок ловушки, не имея возможности преодолеть потенциальный барьер и проникнуть внутрь вещества. В результате их можно накапливать и хранить в полости. Идея о возможности хранения ультрахолодных нейтронов в замкнутой полости за счет полного внешнего отражения принадлежит Я.Б. Зельдовичу.

Очевидно, что эффекты, которые обусловлены наличием у нейтрона ЭДМ, должны расти с возрастанием электрического поля, приложенного к нейтрону, а также с увеличением времени пребывания нейтрона в этом поле. Абсолютная погрешность при измерениях ЭДМ указанным способом, характеризующая чувствительность метода, оценивается как

$\delta (D) = \hbar / (E \tau \sqrt{N})$

Величина $E \tau$ обусловливает экспериментально наблюдаемый эффект, например изменение скорости счета нейтронов в детекторе при изменении направления электрического поля или спина нейтрона. N - полное число зарегистрированных детектором событий за все время измерения. Таким образом, чтобы улучшить чувствительность метода, нужно увеличивать электрическое поле, действующее на нейтрон, время пребывания нейтрона в этом поле, а также стараться собрать в области действия поля как можно больше самих нейтронов.

Существование в веществе сильных межатомных электрических полей $\sim 10^8-10^9$ В/см следует из простых соображений: энергия выхода электронов из вещества лежит в интервале 1-10 эВ, значит, разность потенциалов на атомах и между ними 1-10 В; межатомные же расстояния около $10^{-8}$ см. Эти поля быстро осциллируют в веществе и поэтому при движении частиц обычно усредняются, обращаясь в нуль.

Однако бывают ситуации, например при дифракции нейтронов в монокристаллах, когда, в силу регулярности потенциала кристалла и соответствующей регулярности волновой функции нейтрона в нем, нейтрон может оказаться в сильном электрическом поле на протяжении всего времени прохождения кристалла. Именно это обстоятельство, т.е. эффективное взаимодействие с внутрикристаллическим полем нейтронов при их динамической дифракции по Лауэ в прозрачном нецентросимметричном кристалле, и было использовано при постановке нового - дифракционного - опыта по уточнению верхнего предела на величину ЭДМ нейтрона.

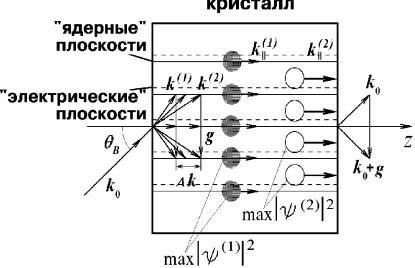
Физика явлений, лежащих в основе метода, следующая. Из динамической теории дифракции следует, что движение нейтрона в кристалле в направлениях, близких к брэгговским, можно описать волнами двух типов $\Psi^{(1)}$ и $\Psi^{(2)}$ . Это две волны, сформированные в результате многократного отражения нейтрона от кристаллографических плоскостей, причем стоячие в перпендикулярном к плоскостям направлении. Дифрагирующие нейтроны в этих состояниях, распространяясь в среднем вдоль плоскостей, оказываются сконцентрированными на "ядерных" плоскостях и между ними соответственно.

В нецентральносимметричных кристаллах для некоторых систем кристаллографических плоскостей положения максимумов электрического потенциала смещены относительно максимумов ядерного потенциала:

$V^{N}(r) = 2V^{N}_{g} \cos(gr)$ ,
$V^{E}(r) = 2V^{E}_g \cos(gr + \phi_g)$ .

Здесь $V^{N}(r)$ - ядерный потенциал, ответственный за дифракцию нейтронов, $V^{E}(r)$ - электрический, g - вектор обратной решетки, характеризующий выбранную систему плоскостей; $2V_{g}^{N}$ , $2V_{g}^{E}$ - амплитуды ядерного и электрического потенциалов соответственно. Величина $\phi_g$ характеризует смещение максимумов ядерного потенциала относительно максимумов электрического. В результате нейтроны в состояниях $\Psi^{(1)}$ и $\Psi^{(2)}$ оказываются в сильных ( $\sim 10^8$ В/см) межплоскостных электрических полях противоположного знака:

$E_g = \pm gV_{g}^{E} \sin {\phi_g}$ .

Наличия таких внутрикристаллических полей еще недостаточно для повышения точности измерения ЭДМ. Важное свойство приведенное на схеме дифракции по Лауэ - возможность увеличить время пребывания нейтрона в электрическом поле кристалла путем перехода к углам Брэгга $\theta_B$ , близким к $\pi/2$ . Причина в том, что при дифракции по Лауэ нейтрон, имея полную скорость v, вдоль кристаллографических плоскостей в среднем движется со скоростью $v \Vert = v \cos \theta_B$ , которая может быть существенно уменьшена по сравнению с v при выборе угла дифракции $\theta_B$ вблизи $\pi/2$ . Поскольку при этом $\cos \theta_B \approx \pi /2 - \theta_B$ , время $\tau = L/v_{\|} \sim (\pi/2 - \theta_B)^{-1}$ растет по мере приближения $\theta_B$ к $\pi/2$ . Максимально близкий к $\pi/2$ угол Брэгга определит максимальную чувствительность метода. Дальнейшее его увеличение, в принципе может оказаться невозможным.

Рис 7

Движение нейтронов вдоль кристаллографических плоскостей при дифракции. Кружками изображены области максимальной концентрации нейтронов в состояниях $\Psi^{(1)}$ и $\Psi^{(2)}$ , здесь частицы двигаются в электрических полях разного знака. k - волновые векторы нейтрона, связанные с его скоростью k=mv/h; так как нейтроны в состояниях $\Psi^{(1)}$ и $\Psi^{(2)}$ оказываются в разных потенциалах, их кинетические энергии, а значит, и k, отличаются. На выходе из кристалла показаны волновые векторы двух продифрагировавших пучков, прямого и отраженного. Их геометрическое расположение определяет условие наблюдения брэгговских пиков дифракции, задающее угол Брэгга.

3. Кварковая модель элементарных частиц

Современная модель нейтрона Читать далее: Существование кварков

Раздел: Физика
Количество знаков с пробелами: 101982
Количество таблиц: 6
Количество изображений: 13

Скачать

... уже после окончания ими школы, это поможет им в дальнейшем при получении профессии и при совершенствовании их профессиональных знаний и умений. 1.2 Психолого-педагогические проблемы формирования целостного миропонимания В Концепции модернизации российского образования на период до 2010 года как основные можно выделить следующие параметры качества образования: 1) научность, 2) ...

Скачать

... за пределами своей дискретности. Завершенная модель построения элементарных частиц должна соответствовать свойствам абсолютного взаимодействия и включать все виды материй, что достигается на основании матричного моделирования элементарных частиц. Конечный уровень построения материи представляет собой частицу лишенную внутренней структуры - пространственная точка (далее в тексте обозначена ...

Скачать

... друг от друга, поэтому их рассматривают как одну частицу — нуклон. Сильное взаимодействие действует на малых расстояниях (10-15 м) и превосходит электромагнитное и гравитационное, но оно уменьшается с увеличением расстояния. Атомное ядро любого химического элемента состоит из протонов и нейтронов, связанных между собой ядерными силами (сильным взаимодействием). Протон - ядро атома водорода имеет ...

Скачать

... может привести к очередной, третьей, научной революции, и физика сделает еще один шаг вперед в своем развитии(9. с. 409). Подводя короткий итог всему вышесказанному, можно отметить, что развитие физики во второй половине ХХ в. привело к открытиям, обладающим такой силой и мощью, которой вполне достаточно как для научно-технической революции, так и для уничтожения всего живого на Земле. Но ученые ...

Главная Новости Рефераты Статьи Вузы

О проекте Соглашение

Наверх

Войти на сайт

Навигация

Похожие работы

0 комментариев

Разделы

Инфо

Следите за новостями