Расчётная часть

2 Расчётная часть

2.1Задание на курсовую работу

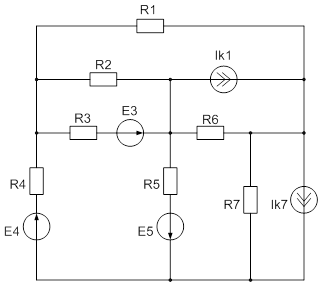
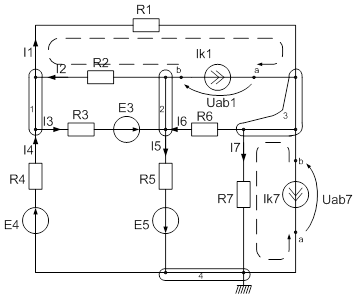
Расчет разветвлённой электрической цепи постоянного тока.

Для заданной электрической цепи необходимо:

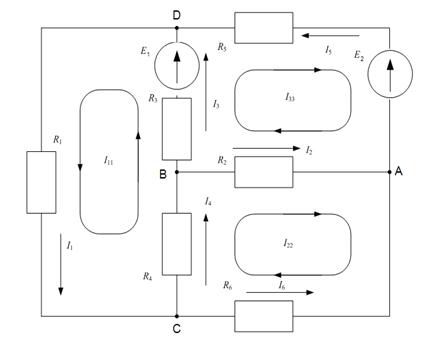
1)     Записать систему уравнений по законам Кирхгофа (без расчетов);

2)     Определить все токи и напряжения методами контурных токов и узловых потенциалов;

3)     Проверить результаты расчетов по уравнениям баланса мощностей;

4)     Построить потенциальные диаграммы для двух замкнутых контуров.

ЭДС=E1=E2=50 В

Резисторы R1=12 Ом

R2=24 Ом

R3=15 Ом

R4=18 Ом

R5=30 Ом

R6=30 Ом

R7=30 Ом

2.2 Составление уравнений по двум законам Кирхгофа.

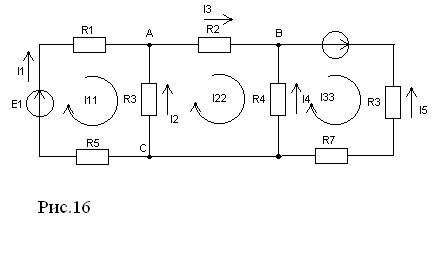
Записываем уравнения по первому закону Кирхгофа для любых двух узлов:

Узел А: I1+I2+I3=0

Узел B: I3+I4+I5=0

1)   Выбираем независимые контуры и направления их обходов.

3) Записываем уравнения по второму закону Кирхгофа для выбранных независимых контуров.

I1*(R1+R6)-I2*R3=E1

I3*R2+I2*R3-I4*R4=0

I4*R4-I5*R7-I5*R5=E2

4) Подставим численное значение:

I1+I2-I3=0

I3+I4+I5=0

I1*(12+30)-I2*15=50

I3*24+I2*15-I4*18=0

I4*18-I5*30-I5*30=50

2.3 Определение всех токов и напряжений методами контурных

токов.

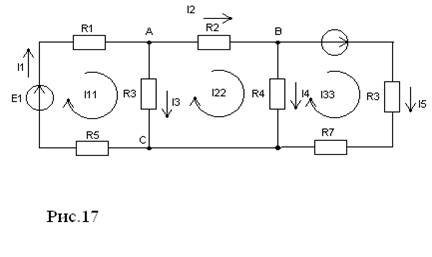
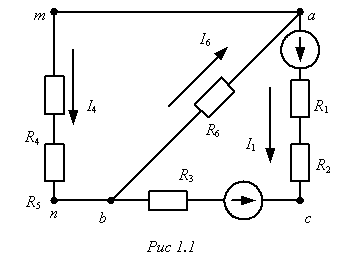
1)   Выбираем независимые контуры:

R6,E1,R1,R6;

R3,R2,R4;

R4,E2,R5,R7;

2)   Полагаем, что в каждом контуре течет свой контурный ток: I11,I22,I33.

3)   Произвольно выбираем их направления.

4)   Записываем уравнения по второму закону Кирхгофа относительно контурных токов, для выбранных независимых контуров:

I11(R1+R3+R6)-I22*R3=E1

I22(R2+R3+R4)-I11*R3-I33*R4=0

I33(R4+R5+R7)-I22*R4=E2

Подставим численные значения:

I11*57-I22*15+0=50

-I11*15+I22*57-I33*18=0

0-I22*18+I33*78=50

5)   Решаем полученную систему уравнений через определители:

Главный определитель:

|57 -15 0|

D= |-15 57 -18| = 253422+0+0-0-17550-18468=217404

|0 -18 78|

Вспомогательный определитель 1:

|50 -15 0|

D1= |0 57 -32| = 222300+0+13500-0-0-16200=219600

|50 -18 78|

Вспомогательный определитель 2:

|57 50 0|
D2= |-15 0 -18| = 0+0+0-0-(-58500)-(-51300)=109800

|0 50 78|

Вспомогательный определитель 3:

|57 15 50|
D3= |-15 57 0| = 162450+13500+0-0-11250-0=164700

|0 -18 50|

I11=D1/D=219600/217404=1.01(A)

I22=D2/D=109800/217404=0.505 (A)

I33=D3/D=-164700/217404=0.757 (A)

I1=I11=1.01 (A)

I2=I22=-0.505 (A)

I3=I11-I22=1.01-0.505=0.505 (A)

I4=I22-I33=0.505-0.757=-0.252 (A)

I5=I33=0.757 (A)

6)Энергетический баланс мощностей

На основании закона сохранения энергии количество теплоты выделяющиеся в единицу времени на резисторах должно равняться

энергии доставляемой за это же время источниками энергии.

SIE=SI²R

E1*I1+E2*I5=I1² *(R1+R5)+I2^2*R2+I3² *R3+I4²*R4+I5²*(R5+R7)

50.5+37.5=32.64+6.120+3.825+0.068+34.382

88.35=77.055 (Вт)

2.4 Метод узловых потенциалов.

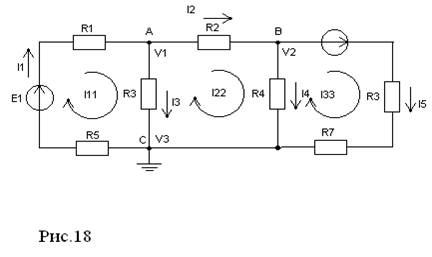1) Выбираем базисный узел (целесообразно за базисный принимать тот узел, в котором пересекается больше всего ветвей):

V3=0

2) Задаемся положительными направлениями узловых потенциалов от базисного узла.

3) Записываем собственные и взаимные проводимости узлов, исключая базисный:

g11=0.0238+0.0416+0.0666=0.132 (Сим)

g22=0.0416+0.0555+0.0166=0.1137 (Сим)

g12=0.0416 (Сим)

4) Введем узловые токи для всех узлов, исключая базисный:

I11,I22

I11=1.1904 (A)

I22= -0.8333 (A)

Узловой ток равен алгебраической сумме токов от действия ЭДС ветвей пересекающихся в данном узле.

Если ЭДС направлено к узлу, то ЭДС записываем со знаком «+»,
в противном случае «-».

5)     Записываем систему уравнений:

V1*g11-V2*g12=I11

V2*g22+V1*g21=I22

g12=g21=0.0416 (Сим)

V1*0.132+V2*(-0.0416)=1.1904

V2*0.1137+V1*(-0.0416)= -0,8333

V1*0.132-V2*0.0416=1.1904

-V1*(-0.0416)+V1*0.132= -0.8333

|0.132 -0.0416|

D= |-0.0416 0.132| = 0.0174-0.0174=0.0157

|1.1904 -0.0416|

D1= |-0.8333 0.132| = 0.1571+0.0346=0.1225

|0.132 1.1904|

D2= |-0.0416 -0.8333| = (-0.1099)-(-0.0495)= -0.0604

V1=D1/D= 0.125/0.0157= 7.8025

V2=D2/D= -0.0604/0.0157= -3.8471

I1=(V3-V1+E1)/(R1+R6)=42.1975/42=1.0047 (A)

I2=(V1-V2)/R2=11.6496/24=0.4854 (A)

I3=(V3-V1)/R3= -7.8025/15= -0.5201 (A)

I4=(V3-V2)/R4= 0.2137 (A)

I5=(V3-V2+E2)/(R5+R7)= 53.8471/60=0.8974 (A)

2.5 Энергетический баланс мощностей

На основании закона сохранения энергии количество теплоты выделяющиеся в единицу времени на резисторах должно равняться энергии доставляемой за это же время источниками энергии.

SIE=SI²R

Энергетический баланс мощностей методом контурных токов:

E1*I1+E2*I5=I1² *(R1+R5)+I2^2*R2+I3² *R3+I4²*R4+I5²*(R5+R7)

50.5+37.5=32.64+6.120+3.825+0.068+34.382

88.35=77.055 (Вт)

Энергетический баланс мощностей методом узловых потенциалов:

E1*I1+E2*I5=I1² *(R1+R5)+I2^2*R2+I3² *R3+I4²*R4+I5²*(R5+R7)

50.235+44.87=42.3948+5.6547+4.0575+0.8208+48.318

95.105=101.245 (Вт)

2.6 Построение потенциальных диаграмм для двух замкнутых контуров.

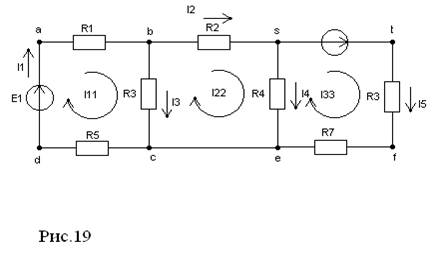Va=0

Vb=Va-I1*R1= -12.05 B (12;-12.0564)

R=12 (Ом)

Vc=Vb-I3*R3= -19.8579 C (27;-19.8579)

R=R+15 (Ом)

Vd=Vc-I1*R6= -50.02 D (57;-50.02)

R=R+30 (Ом)

Va=Vd+E1= 0 A (57;0)

R=57 (Ом)

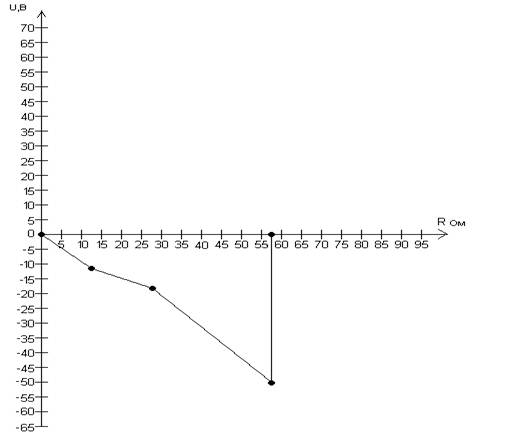
Рис. 20

Vt=0

Vf=Vt+I5*R5= 22.71 F(30;22.71)

R=30 (Ом)

Ve=Vf+I5*R7= 45.42 E(60;45.42)

R=R+30 (Ом)

Vs=Ve-I4*R4= 40.884 S(78;40)

R=R+18 (Ом)

Vt=Vs-E2= 10 T(78;10)

R=78 (Ом)

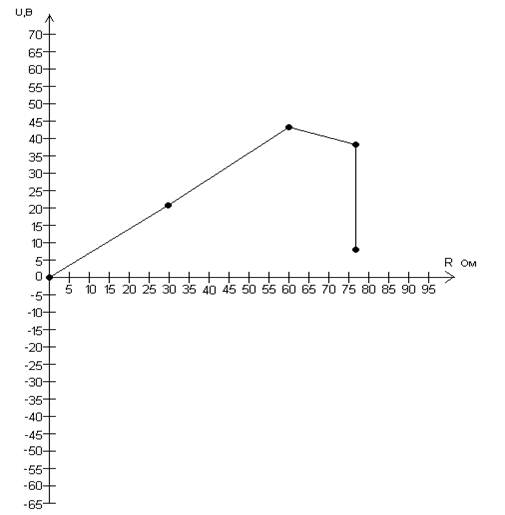
Рис. 21

Заключение.

В процессе выполненных заданий я проанализировал схему разветвленной электрической цепи постоянного тока, в полном объёме изучил её работу, различные методы определения токов и напряжений, узловых потенциалов, проверил на практике различные законы Ома, законы Кирхгофа, баланс мощностей. Наглядно графическим методом показал зависимость напряжения от сопротивления.

Список литературы.

Дятлаф А.А. Яворский Б.М. Курс физики//Высшая школа . 2000г.

Башин М. Л. Теория электрических цепей // Электротехника. 2001г.

Кринина М. Физика для высшеё школы // Физфакультет. 2000г.

Савельев И.Р. Курс общей физики // Москва 2000г.

Шабанова А.Р. Лекции // 2003г.