Обсуждение понятия скорости тела и построения полей времени в покоящейся и движущейся системах отсчета

4.10. Обсуждение понятия скорости тела и построения полей времени в покоящейся и движущейся системах отсчета.

Казалось бы, понятие скорости тела, как пройденного пути за определенный промежуток времени:

настолько ясно, что не требует вообще никаких пояснений. Конечно, если тело движется неравномерно, то надо вводить в рассмотрение мгновенную скорость

но не об этом сейчас речь. Вместе с тем в связи с данным определением скорости необходимо, однако, обсудить весьма существенный физический вопрос.

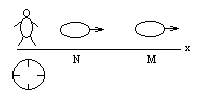
Чтобы лучше представить себе ситуацию, рассмотрим конкретный эксперимент, проводимый для измерения скорости тела. Пусть имеется движущееся тело и пусть оно в какой-то момент времени проходит или пролетает через то место N , где мы сами сейчас находимся. Засечём этот момент t1 на имеющемся у нас измерителе времени - часам.

Предположим, что мы находимся в месте N и наблюдаем из этого места за нашим движущимся телом. Через некоторое время, скажем в момент времени t2 , зарегистрированным по нашим часам, тело проходит через другое место M, расстояние до которого S2-S1 от нашего места N, мы можем измерить заранее. Тогда скоростью тела мы назовем отношение

Вроде бы всё совершенно ясно. Но это не так. Мы должны учесть, что когда мы увидели, что тело проходит через место M ,мы на самом деле просто зарегистрировали световой сигнал, приходящий к нам из места M, свидетельствующий о совпадении тела и места M. Так как сигнал распространяется с некоторой конечной скоростью С, то мы должны это учесть и ввести поправку на время распространения сигнала от места M до места N, т.е. поправку на время запаздывания .

Таким образом, мы должны в формуле для скорости V взять не момент t2, непосредственно экспериментально наблюдаемый и зафиксированный по нашим часам, а момент

и скоростью тела должны на самом деле назвать величину

которая лишь незначительно больше величины V, если тело движется не слишком быстро.

Так как скорость света C очень большая ( С=300000 км /c), то рассматриваемая поправка, конечно, будет для реально наблюдаемых движений тел на Земле чрезвычайно малой .

Однако она становится тем больше, чем дальше удалено место М от места N и чем скорее движется тело. Если скорость V тела будет близка к скорости света, то поправка будет очень большой .

Именно эта поправка в определении скорости тела и учитывается в специальной теории относительности .

Здесь следует сказать, что наше субъективное ощущение об окружающем нас мире в некоторый данный момент времени, действительно субъективно и неправильно. Дело в том, что удаленные предметы мы видим такими, какими они были в более ранние моменты времени, чем видимые нами близкие от нас предметы .

Скажем, мы видим на улице “одновременно” идущих людей, здания, Солнце .Но ведь, на самом деле, Солнце мы видим не в тот момент, в который мы на него смотрим, а в момент примерно на 8,5 минут раньше (так как время распространения света от Солнца до Земли составляет примерно 8 мин. 20 сек. ). А если мы “одновременно” взглянем в телескоп на удаленные от нас звезды и галактики, то галактики на самом деле сейчас мы видим в такие моменты, когда мы ещё и сами не родились, и даже ещё не появилась наша Земля и наша Солнечная система .

Таким образом, обсуждая понятие скорости движущегося тела, нам надо обязательно разобраться, что мы понимаем под временем в различных местах пространства. Чтобы экспериментально исследовать перемещение тела в пространстве с течением времени, лучше всего иметь локальные согласованные друг с другом измерители времени - часы, расставленные во всех точках пространства. Тогда совсем не нужно будет думать о поправках в отсчётах времени, скоростях световых сигналов и т.д. Множество локальных времен в различных точках системы отсчета образует то, что мы будем называть полем времени.

Построим сначала поле времени в “покоящейся“ системе отсчета К. Для этого в начале отсчета О организуем “производство” совершенно одинаковых, идентичных, измерителей времени - часов, ход которых, по возможности, одинаков. Затем эти измерители времени достаточно осторожно разнесём по различным точкам пространства M, N,… .

Если бы все эти часы мы сначала синхронизовали (выставили бы на них одинаковые показания времени), а затем разнесли по различным точкам пространства, то показания часов, помещенных в различных точках, мы могли бы и назвать временем в системе отсчета К.

Так поступать, однако, нельзя. Чтобы перенести часы, например из точки «О» в точку М, мы должны сначала эти часы в точке О ускорить, затем передвинуть, а затем замедлить для остановки в точке М. При ускоренном и замедленном движениях при этом ход часов обязательно нарушится и в показания времени будет введена неконтролируемая ошибка.

Поэтому поступим так, как поступил Эйнштейн в работе 1905 г. Будем все часы синхронизировать не в начале координат, до их разнесения, а лишь после того, как мы уже их разнесли и установили в разных точках пространства системы отсчета К.

Синхронизацию проведем при помощи бесконечно коротких световых сигналов, которые будем испускать из начала координат О. В момент времени t = 0, фиксируемый по часам в точке О, мы испустим из точки О сигнал по направлению к точке М, и зарегистрируем момент прихода этого сигнала в точку М по часам в этой точке М и, наконец, выставим на часах в точке М время

,

где r - расстояние между точками N и M. Величиной скорости c при этом мы просто зададимся, т.е. возьмем в качестве нее любое положительное число.

Очевидно, что если теперь, с помощью синхронизированных описанным способом локальных часов, мы будем измерять скорость используемых для синхронизации импульсных световых сигналов, то получим естественно значение c, причем эта скорость окажется изотропной, т.е. не зависящей от выбора направления в пространстве.

Однако надо отчетливо понимать, что это не измерение скорости света, так как само понятие времени мы установили с помощью световых сигналов и значением скорости света с мы просто задались.

Вместе с тем, для краткости, будем называть величину с - «скоростью света»(более точно, скоростью света в системе отсчета К ).

Теперь в точности таким же образом, с помощью импульсных световых сигналов, установим поле времени в «движущейся системе отсчета К'.

Конечно, можно было бы построить поле времени в системе отсчета К' и другим способом. Мы могли бы, например, рассудить следующим образом. Гипотетическая электромагнитная среда - эфир, колебаниями которой является свет, покоится в системе отсчета К, поэтому в системе отсчета К мы имеем свет в покоящейся среде. В системе отсчета К' имеем свет в движущейся среде, а поэтому скорость светового импульса, испущенного, например, в положительном направлении оси x' в системе отсчета К' равна не с, а c - u, а в отрицательном направлении оси x' равна c + u, где u - скорость движения системы К' относительно системы К. Но так сейчас мы поступать не будем, а просто примем, что в системе отсчета К' световые импульсы распространяются в точности так же, как в системе К. В этом заключено однако серьезное физическое предположение. При построении поля времени в системе отсчета К' используем то же самое число с, что и в системе отсчета К. Последнее по существу условное допущение, следуя работе Эйнштейна 1905 г., иногда неправильно называют «законом постоянства скорости света в инерциальных системах отсчета». Как мы видим, это вовсе не закон, а говоря словами Пуанкаре, «плод совершаемого неосознанного условного соглашения».

Приступим теперь к кинематическому выводу преобразований Лоренца. Объектом нашего рассмотрения будет так называемое мгновенное точечное событие, т.е. событие, происходящее в очень малом месте пространства и за очень короткий промежуток времени. Например, из некоторой точки N в фиксированный момент времени t = t₀испустим импульсную сферическую бесконечно тонкую световую волну.

Уточняем - испускаем не периодическую гармоническую волну, а очень короткий световой импульс. Испускание светового импульса в момент времени t = t₀в точке N и есть пример мгновенного точечного события. Разумеется, мгновенные точечные события могут быть какие - угодно.

Приведем еще один пример. Твердый стержень AB пусть движется в положительном направлении оси x.

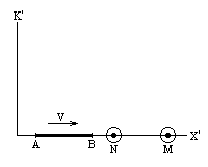
Мгновенным точечным событием теперь можно считать событие, заключающееся в совпадении, например, левого конца A стержня с фиксированной точкой N оси x. Другим мгновенным точечным событием является совпадение в какой-то момент времени правого конца B с фиксированной точкой M на оси x.

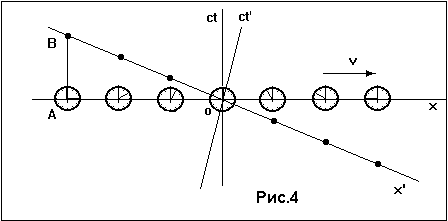
Теперь, одно и то же какое-нибудь мгновенное точечное событие будем изучать с помощью наблюдений его в двух инерциальных системах отсчета K и K', или в двух системах координат, движущихся равномерно и прямолинейно относительно друг друга - «покоящейся» системы К и «движущейся» системы K', - движущейся со скоростью u вдоль оси x относительно покоящейся системы отсчета, причем в обеих этих системах координат размещены локальные часы, синхронизированные так, как мы разъяснили выше.

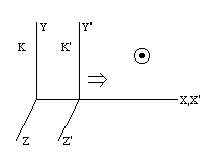
Пусть x, y, z, t - координаты и время нашего мгновенного точечного события, отсчитанные в системе отсчета К. Пусть x', y', z', t' - координаты и время нашего мгновенного точечного события, отсчитанные в системе отсчета К'.

Ради простоты дальше будем рассматривать только координаты x и x', считая что всегда y' = y и z' = z. Тогда в системах отсчета К и К' координаты одного и того же мгновенного точечного события будут x, t и x', t' соответственно, причем «координатой» будем называть не только координату x, а координату и время - x, t.

Так как эти числа относятся к одному и тому же событию (существующему в природе вне зависимости от наличия или отсутствия систем отсчета К и К'), то очевидно должны существовать однозначные математические зависимости вида

x' = j(x, t), t' = y(x, t).

Формулы указанных зависимостей будем называть формулами преобразования координат мгновенного точечного события (любого) от системы отсчета K системе отсчета К'.

Наша конечная цель - найти вид функций j и y в приведенных формулах преобразования. Чтобы это сделать, обратимся к так называемым основным, исходным для нас, соотношениям, которые мы сейчас сформулируем.

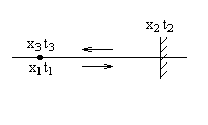
Рассмотрим три следующих мгновенных точечных события. Опишем их сначала в системе отсчета К. Пусть в точке x₁ оси x в момент t₁ мгновенно был испущен короткий световой импульс в положительном направлении оси x. Пусть в момент времени t₂ этот импульс оказался в точке x₂ оси x, в которой он зеркально отразился и стал двигаться в отрицательном направлении оси x. Пусть, наконец, в момент времени t₃ этот световой импульс снова оказался в исходной точке, так что x₃ = x₁.

Посмотрим теперь на три указанных мгновенных точечных события с точки зрения системы отсчета K'. Мы увидим, что в точке x₁' в момент времени t' был испущен в положительном направлении оси x' короткий световой импульс, который в момент времени t₂' достиг точки x₂', отразился в ней и в момент времени t₃' оказался в точке x₃', причем теперь x₃' № x₁'.

Согласно описанным выше процедурам построения полей времени в системах отсчета K и K' имеем следующие очевидные соотношения в системе отсчета K:

x₃ = x₁

и в системе отсчета K':

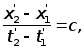
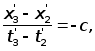
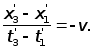
Точка x₁ = x₃ на оси x системы отсчета K движется со скоростью u в отрицательном направлении оси x', если ее наблюдать в системе отсчета K'.

Мы сформулировали шесть основных соотношений, исходя из которых мы теперь найдем вид функций j и y.

Нахождение функции j. Составим функциональное уравнение для определения функции j. Представим три соотношения для системы отсчета K в следующем виде:

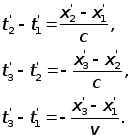
Вычитая первое соотношение из третьего, получаем

Используя второе соотношение, отсюда приходим к равенству

Следовательно,

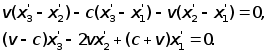
или

Таким образом, видим, что функция j удовлетворяет следующему функциональному уравнению:

В этом уравнении величины x₁, t₁, x₂, t₂, x₃, t₃, однако, не независимы, а связаны нашими основными соотношениями для системы отсчета K. Учтем наличие этих соотношений и оставим независимыми только следующие три величины: x₁, x₂ и t₁. Величины x₃, t₂ и t₃ можно выразить через указанные независимые величины. Действительно, из первого соотношения получаем

следовательно,

Далее, из второго соотношения имеем

а следовательно,

мы воспользовались выражением для t₂ и условием x₃ = x₁.

Таким образом, получаем следующее окончательное функциональное уравнение для определения функции j:

которое должно выполняться для произвольных значений x₁, x₂ и t₁.

Приступим к решению полученного функционального уравнения. Начнем с того, что продифференцируем это уравнение по x₂. Получим тогда соотношение, которое будем называть продифференцированным функциональным уравнением

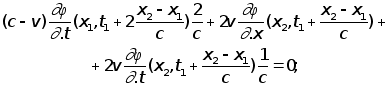
на общую двойку можно сократить все три слагаемые (производная от последнего, третьего слагаемого в исходном функциональном уравнении равна нулю, так как оно не зависит от ). В полученном дифференциальном уравнении положим теперь и . Тогда придем к следующему дифференциальному уравнению:

Общее решение полученного очень простого дифференциального уравнения легко найти, если перейти к переменным и и показать, что в новых переменных это уравнение имеет вид

Так получаем, что общее решение рассматриваемого дифференциального уравнения имеет вид

где F — пока произвольная функция.

Найдем вид этой функции. Для этого подставим полученную формулу для в наше дифференциальное функциональное уравнение. Получим тогда следующее функциональное уравнение:

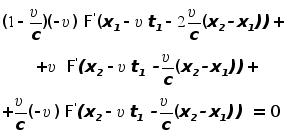
После элементарных алгебраических преобразований, отсюда получаем, что

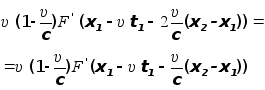
или

Так как при произвольных аргументы функций в правой и левой частях равенства различны и могут принимать совершенно произвольные значения, то приходим к заключению, что

а следовательно,

F

где — некоторые постоянные, которые нам еще предстоит найти.

Итак, мы показали, что исходная функция имеет следующий вид:

где — некоторые пока не определенные постоянные.

Нахождение функции . Найдем теперь аналогичным образом функцию . Три основных соотношения для системы отсчета представим в виде:

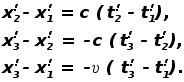
Вычитывая первое соотношение из третьего и сравнивая результат со вторым соотношением, получаем уравнение

т.е. уравнение

Видим, что функция удовлетворяет следующему функциональному уравнению:

в котором величины не независимые, а связаны нашими основными соотношениями для системы отсчета К. Используя эти соотношения, оставим независимыми только следующие три величины и. Величины и выразим через указанные величины:

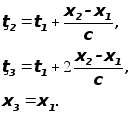
Таким образом, приходим к следующему основному функциональному уравнению для искомой функции:

которое выполняется при произвольных значениях и.

Приступим к решению полученного функционального уравнения. Начнем с того, что продифференцируем его по :

производная последнего, третьего слагаемого в исходном функциональном уравнении равна нулю, так как оно не зависит от . Положим теперь в выведенном уравнении,

и тогда придем к дифференциальному уравнению

или уравнение

Легко найти общее решение последнего дифференциального уравнения. Для этого надо перейти только к новым независимым переменным

и показать, что в новых переменных уравнение имеет вид

Таким образом получаем общее решение нашего дифференциального уравнения:

в котором — пока произвольная функция.

Найдем вид этой функции. Подставим полученное выражение для функции в продифференцированное функциональное уравнение. Получим тогда соотношение

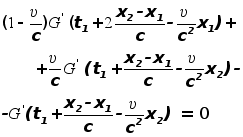
или соотношение

Так как аргументы у функций в правой и левой частях равенства при произвольных значениях

и совершенно произвольны, то получаем, что

а следовательно,

где — пока неопределенные постоянные.

Определение констант . Мы получили, что формулы преобразований координат и времен произвольного мгновенного точечного события в инерциальных системах отсчета и имеют вид

Для нахождения констант привлечем дополнительное требование.

Требование 1. Предположим, что общие начала отсчета координат и времени в системах отсчета K и согласованы таким образом, что мгновенное точечное событие с координатами 0,0 в системе отсчета K имеет в системе отсчета координаты 0,0 ( тоже нулевые координаты),и наоборот.

Применяя вышеприведенные формулы преобразования к событию 0,0 получаем, что и поэтому формулы преобразования координат мгновенно точечного события приобретают следующий вид:

Теперь неопределенными остались только константы и .

Учтем теперь то обстоятельство, что формулы преобразования мы получили как следствия наших шести основных соотношений. Подставим поэтому полученные простые формулы обратно в эти исходные основные соотношения и установим ограничения на значения констант и . Имеем:

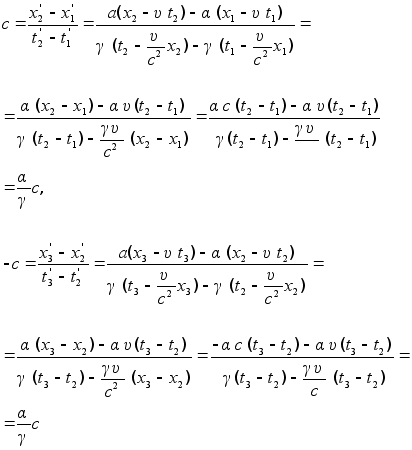
Таким образом, приходим к заключению, что константы и равны друг другу:

=

и поэтому формулы преобразования координат мгновенного точечного события имеют следующий вид:

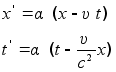
где — пока что неопределенная постоянная.

Разрешим теперь эти формулы преобразования относительно и . Имеем уравнения

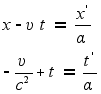
Следовательно,

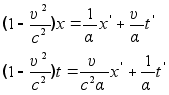
и поэтому

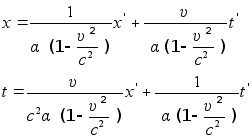
Полученные формулы сопоставим с формулами преобразования:

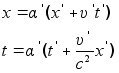
которые получаются с помощью рассуждений, совершенно аналогичных приведенным выше, но с заменой систем отсчета K и друг на друга. Следует при этом только учесть, что система отсчета K движется относительно системы отсчета не в положительном, а в отрицательном направлении оси с некоторой положительной скоростью (положительной), определенной в системе отсчета K . Здесь — некоторое пока неизвестное нам число.

Сравнивая друг с другом приведённые пары формул преобразований, приходим к заключению, что имеют место следующие четыре равенства:

из которых непосредственно заключаем, что

и что величины a и a’ удовлетворяют соотношению

Таким образом, мы показали, что имеются следующие формулы преобразований координат x, t и x’, t‘ мгновенного точечного события в системах отсчета K и K’:

и

где величины a’ и a связаны вышеуказанным соотношением.

Чтобы найти числа a’ и a, выставим ещё одно требование. Обратим внимание, что пока мы до конца не условились о выборе основных единиц измерения длинны и времени в системах отсчета K и K ’. Разумеется, отчасти этот выбор уже был выше ограничен требованием, чтобы скорость света в обеих системах отсчёта давалась одним и тем же числом c, которое мы учли, т.е. мы уже согласовали отчасти единицы измерения скоростей в системах K и K’. Но единица скорости есть только отношение единиц длины и времени. Поэтому остаётся произвол в выборе единицы измерения либо длины, либо времени. Фиксируем теперь окончательно этот произвол с помощью следующего требования.

Требование 2. Длины l и l’ двух покоящихся в системах отсчёта K и K’ стержней одинаковой собственной длинны l0 (измеренной в этих системах отсчёта, в которых каждый из этих стержней покоится), измеренные, соответственно, в системах отсчёта K и K’ , относительно которых эти стержни движутся одинаковы.

Возьмём стержень длинны l0 , покоящийся в “движущейся” системе отсчёта K’. Пусть он лежит на оси x’ и его левый конец пусть имеет координату x’A , а правый - координату x’B

Из мерим длину этого стержня в “покоящейся” системе отсчёта K. Пусть в одинаковые моменты времени tA и tB ( tA = tB ) левый и правый концы стержня, движущегося в системе отсчёта K, имели координаты xA и xB. (События A и B соответственно). Нам надо составить разность xA - xB = l , чтобы найти длину движущегося со скоростью u стержня, длина которого равна l0 в покоящейся системе координат.

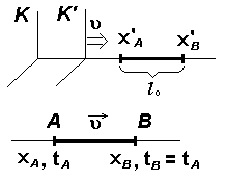
Согласно уже выведенным формулам преобразований координат и времён мгновенных точечных событий, имеем соотношения:

Вычтем из и учтём условие Тогда получим

Таким образом, имеем соотношение

Если теперь, наоборот, взять стержень длины l0 , расположенный в “неподвижной” системе отсчёта K , и измерить его длину l’ в “движущейся” системе отсчёта K’ , то для этой длины, рассуждая аналогично, получаем соотношение

Потребуем теперь, чтобы Тогда мы придём к равенству , а следовательно, с учётом выведенного соотношения

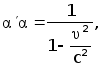
к равенствам

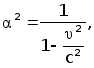
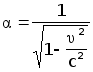
Знак минус перед корнем не подходит, так как не удовлетворяет очевидному требованию, что a = 1 при u = 0 , когда мы имеем формулы тождественных преобразований.

Длина движущегося стержня, как видим, меньше его собственной длины l0 . Движущийся стержень как бы сокращается вдоль направления своего движения. Однако это не истинное, а кажущееся сокращение, более точно, это исключительно кинематический эффект, целиком обязанный принятому определению локального поля времени в движущейся системе отсчёта.

Итак, мы вывели с помощью исключительно кинематических рассуждений следующие формулы преобразований:

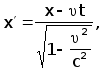
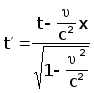
которые называют формулами преобразований Лоренца.

В заключение заметим, что кроме кажущегося, чисто кинематического сокращения длинны движущегося стержня в рассматриваемой кинематике, основанной на описаных выше процедурах построения полей времени в системах отсчёта K и K’ , имеется ещё и эффект кажущегося замедления хода движущихся часов.

Пусть мы имеем часы, неподвижные в “движущейся” системе K’ , находящиеся в точке x’A = x’B . Пусть в них произошел один период колебаний, начавшийся в момент времени t’A (событие A) и окончившийся в момент времени t’B (событие B), так что t’B - t’A = t0 , где t0 - период колебаний часов в “собственной” системе отсчёта

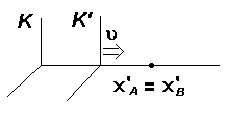
(где они покоятся). Обозначив через xA , xB , tA и tB координаты событий A и B в системе отсчёта K , получаем

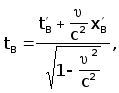
Вычитая второе равенство из первого для кажущегося периода колебаний t часов, определённого в “движущейся” системе K’ имеем следующую формулу

так как x’A = x’B . Следовательно, окончательно получаем формулу

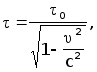
для кажущегося, т.е. кинематического, замедления хода движущихся часов.

4.12 Кинематический вывод преобразований Галилея.

Введём теперь, рассуждая совершенно аналогично тому, как мы это делали при выводе формул преобразований Лоренца, формулы преобразований Галилея, изменив процедуры построения полей времени в инерциальных системах отсчета K и K ’.

Построение полей времени в системах отсчета K и K ’. Будем теперь считать, что в системе отсчёта K среда, возбуждениями которой является свет, покоится. Тогда относительно системы отсчёта K’ эта Среда будет двигаться со скоростью u в отрицательном направлении оси x’.

Процедуру построения локальных времён и синхронизации часов в системе отсчёта K оставим прежней. Но процедуру построения локальных времён в системе отсчёта K’ изменим. При синхронизации часов, помещённых в точке M но оси x’ с координатой x’M>0 , с помощью короткого импульсного светового сигнала, выпущенного из начала координат x’ = 0 в начальный момент времени t’ = 0, в момент прихода сигнала в точку M , на часах в точке M теперь поставим не время r/c , где r - расстояние между O и M , а время

r .

c + u

Аналогично поступим с точкой M на оси x’ с координатой x’M0 , с помощью короткого импульсного светового сигнала, выпущенного из начала координат x’ = 0 в начальный момент времени t’ = 0, в момент прихода сигнала в точку M , на часах в точке M теперь поставим не время r/c , где r - расстояние между O и M , а время

r .

c + 

Аналогично поступим с точкой M на оси x’ с координатой x’M

Похожие работы

Физика (основные формулы)

Скачать

33451

1

3

... силы тока от напряжения носит название закон Ома. Согласно закону Ома, для участка цепи сила тока прямо пропорциональна приложенному напряжению U и обратно пропорциональна сопротивлению проводника R. Основная электрическая характеристика проводника – сопротивление. Сопротивление зависит от материала проводника и его геометрических размеров. , где S – площадь поперечного сечения (м2, мм2 ) l – ...

Исторические проблемы физики. Сила, масса, инерциальная система отсчета

Скачать

35347

0

0

... 1, т.к. она зависит не только от тела 1, но и от тела 2, иными словами с изменением тела 2 ускорение меняется: . Сделать это ускорение не зависящим от тела 2 можно путем перехода к другой системе отсчета (названной инерциальной СО или ИСО), движущейся ускоренно относительно СО1 (самого тела 1) с некоторым ускорением . Найти ИСО значит определить , зная . Пусть даны тело 1 совместно с его системой ...

Основные концепции физики ХХ века

Скачать

106409

0

0

... силы, теперь обречено постоянно думать над тем, как распорядиться ими. Эта проблема человечества в практически обозримое время - вечная. Поэтому человечество должно научиться жить с этой проблемой. Концепции физики элементарных частиц а) Современный статус понятия Элементарной частицы Представление о том, что все во Вселенной делится на вещество и силы, бытующие и в настоящее время, возникло ...

Классическая физика: самоорганизующиеся системы и микромир

Скачать

127339

0

4

... полюсов. Самоорганизация эти поля сохраняет. Из таких колебательных систем сами, как мозаика из магнитов, складываются “классические” самоорганизующиеся модели микромира. Не будем утверждать, что здесь изложены единственно правильные варианты решений "принципиально неразрешимых" задач классической физики. Важно было показать, что такие решения есть - вопреки самым авторитетным уверениям всей ...