Навигация
Основные идеи метода характеристик[6]
1.4. Основные идеи метода характеристик[6]
В данном разделе рассмотрим метод характеристик. Любое линейное дифференциальное уравнение второго порядка (при двух независимых переменных) может быть записано в следующем виде:
|
| (1.4.1) |
где а, b, с, d, e, f, g — заданные непрерывные функции от x и y (или в частном случае, постоянные).
Попытаемся упростить это уравнение с помощью замены независимых переменных:
|
| (1.4.2) |
Здесь
и
— новые
независимые
переменные.
Функции
и ,
связывающие
новые переменные
со старыми,
будут подобраны
позднее; пока
же мы будем
считать их
дифференцируемыми
нужное число
раз. Кроме того,
будем считать,
что система
уравнений
(1.4.2)
может быть
однозначно
разрешена
относительно
х и
у; это
надо
понимать следующим
образом: если
функции
и
и отображают
некоторую
область G
плоскости Оху
в область
G*
плоскости O,
то при этом
каждой точке
(
,)
области G*
соответствует
только
одна точка
области G
(иначе
говоря, отображение
области G
на G*,
даваемое функциями
и ,
является взаимно
однозначным).
Как
известно, для
этого достаточно,
чтобы якобиан
преобразования
(т. е. определитель 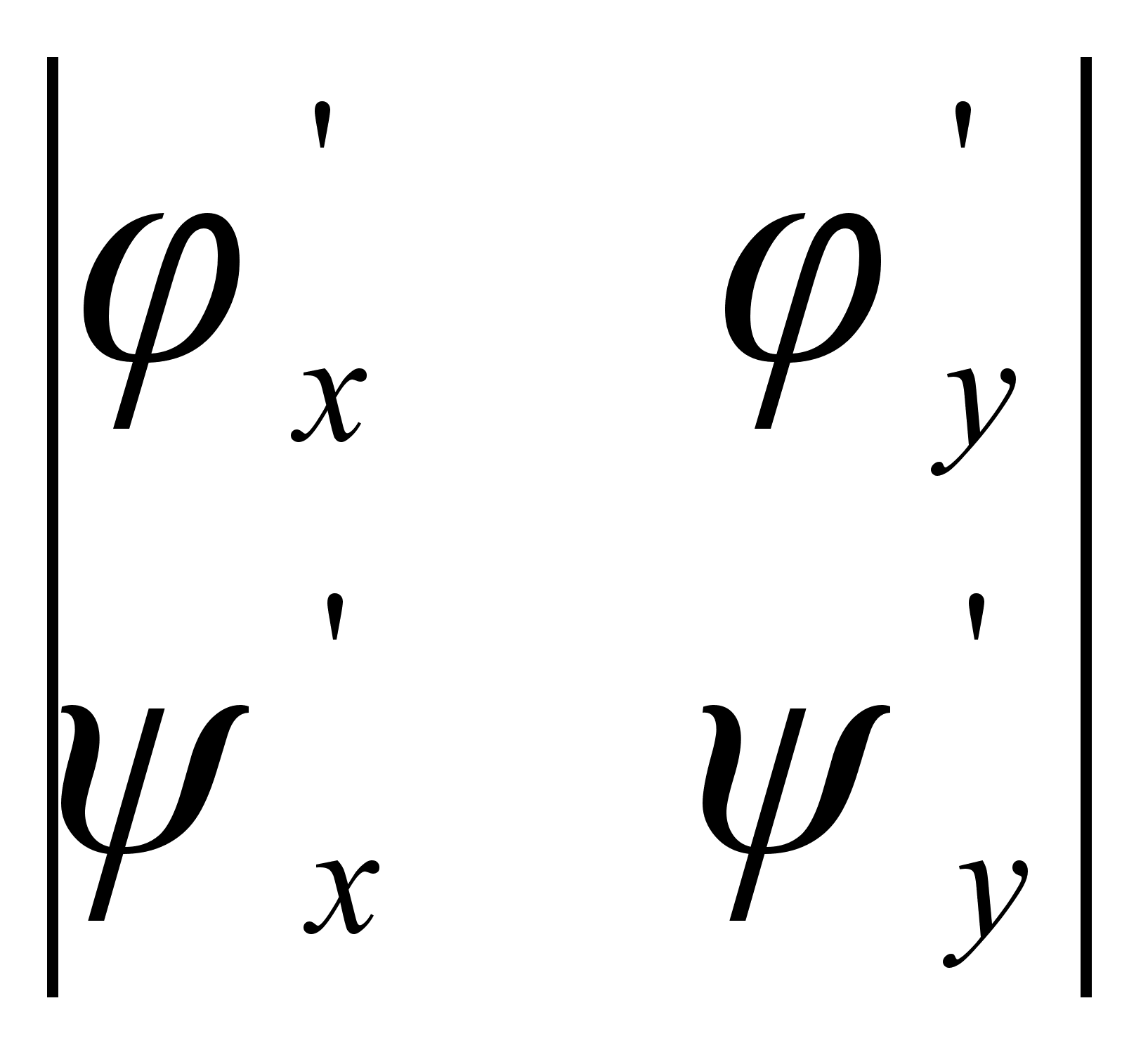 )
нигде в области
G
не обращался
в нуль.
)
нигде в области
G
не обращался
в нуль.
Для того чтобы сделать требуемую замену переменных, выразим частные производные от функции u по х и у через производные от и по и :
|
| (1.4.31) |
|
| (1.4.32) |
Это
записано на
основании
правила дифференцирования
сложной функции
от двух переменных
(здесь u
зависит от
и ,
которые,
в свою очередь,
зависят от x
и у).
Для того чтобы
выразить ![]() ,
через производные
по
и ,
учтем формулу
(1.4.31)
и применим
снова правило
дифференцирования
сложной функции:
,
через производные
по
и ,
учтем формулу
(1.4.31)
и применим
снова правило
дифференцирования
сложной функции:
|
|
Следовательно,
|
| (1.4.41) |
Аналогично найдем:
|
| (1.4.42) |
|
| (1.4.43) |
Правые
части равенств
(1.4.31),
(1.4.32),
(1.4.41),
(1.4.42),
(1.4.43)
представляют собой линейные
функции относительно
частных производных
![]() ,
,
![]()
![]()
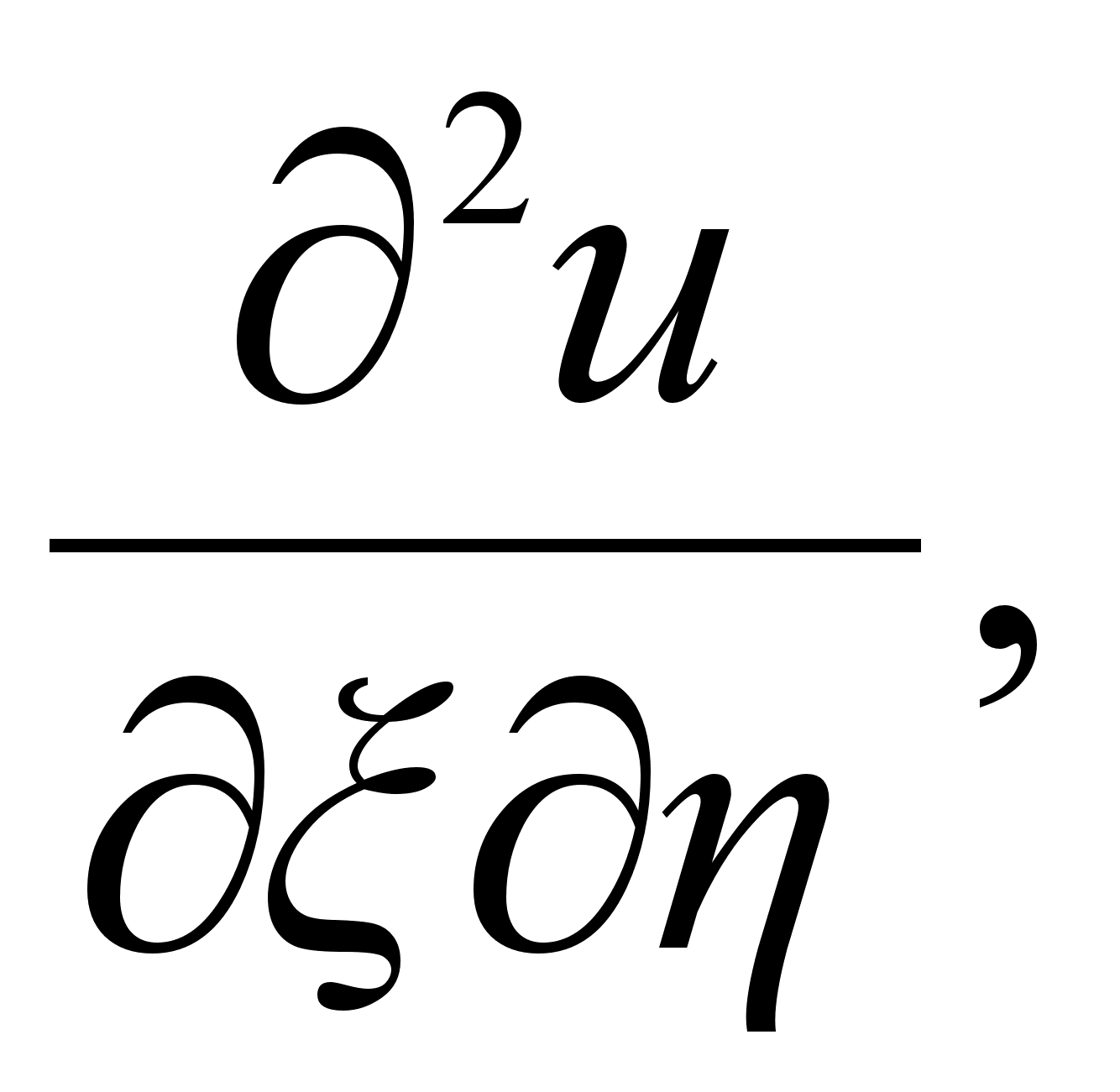
![]() Подставляя
u'x,
u'y,
u'xx,...
из
этих формул
в уравнение
(1), мы получим
снова линейное
уравнение
второго порядка
с
неизвестной
функцией и
и
независимыми
переменными
и :
Подставляя
u'x,
u'y,
u'xx,...
из
этих формул
в уравнение
(1), мы получим
снова линейное
уравнение
второго порядка
с
неизвестной
функцией и
и
независимыми
переменными
и :
|
| (1.4.5) |
где
|
| (1.4.5’) |
a
![]() — функция,
линейная относительно
и’
, u’
, u
.
— функция,
линейная относительно
и’
, u’
, u
.
Уравнение (1.4.5) становится особенно простым, если в нем коэффициенты а и с окажутся равными нулю. Для того чтобы первоначально заданное уравнение (1.4.1) можно было привести к такому простому виду, надо в нем сделать замену переменных
|
|
подобрав функции и так, чтобы они являлись решениями уравнения:
|
| (1.4.6) |
Это уравнение является нелинейным уравнением в частных производных первого порядка. Следующая теорема покажет, как связаны его решения с общим решением некоторого обыкновенного уравнения.
Теорема. Для того чтобы функция z = f(x, у) во всех точках области G удовлетворяла уравнению (6), необходимо и достаточно, чтобы, семейство
|
| (1.4.7) |
было общим интегралом уравнения
|
| (1.4.8) |
в той же области G.
Доказательство. Необходимость. Пусть z = f(x, у)— решение уравнения (1.4.6). Рассмотрим семейство кривых f(x, у) — k и докажем, что любая кривая этого семейства удовлетворяет уравнению (1.4.7).
В любой точке, лежащей на кривой f(x, у) = k (где k — фиксировано), выполняется следующее равенство:
|
|
действительно вдоль данной кривой функция f(x, у) постоянна, и поэтому ее полный дифференциал равен нулю.
Следовательно, всюду на кривой имеет место равенство:
|
|
обозначим каждое из этих отношений через ; тогда
|
|
Подставляя эти выражения для dx и dy в левую часть уравнения (1.4.8), получим:
|
|
Выражение, стоящее в квадратных скобках, равно нулю, так как, по условию, функция f(x, у) есть решение уравнения (1.4.6). Следовательно, во всех точках нашей кривой имеет место равенство
|
|
откуда вытекает, что она является интегральной кривой уравнения (1.4.8).
Итак, любая кривая вида f(x, у) = k является интегральной кривой уравнения (1.4.8); с другой стороны, через каждую точку области G проходит кривая такого вида; это вытекает из того, что функция f(x, у) определена всюду в области G и поэтому, например, через точку (х0, у0) проходит кривая f(x,y)=f(x0,y0).
Отсюда следует, что семейство f(x, у) = k является общим интегралом уравнения (1.4.8).
Достаточность. Пусть семейство f(х, у)= k будет общим интегралом уравнения (1.4.8). Возьмем произвольную точку (х0, у0) из G и выделим ту кривую семейства, которая проходит через эту точку:
f(x, у) = k0.
Так же, как и при доказательстве необходимости, убеждаемся, что всюду вдоль этой кривой выполняется равенство
|
|
откуда
|
| (1.4.10) |
Так как кривая является интегральной кривой уравнения (1.4.8), то при подстановке в это уравнение dx и dy из (1.4.10), получим тождество:
|
|
или, после сокращения на 2:
|
|
В частности, в точке (х0, у0) имеет место:
|
|
Но последнее равенство означает, что функция двух переменных f(x, у) удовлетворяет в точке (х0, у0) уравнению (1.4.7). Так как точка (х0, y0) была взята произвольно в области G, то функция f(x, у) удовлетворяет уравнению (1.4.7) во всех точках этой области, т. е. эта функция является одним из решений уравнения (1.4.7).
Таким образом, теорема доказана.
Рассмотренная теорема открывает путь для упрощения исходного уравнения (1.4.1). Для этого сначала составляем вспомогательное уравнение (1.4.8); оно называется характеристическим уравнением для данного уравнения (1.4.1). Характеристическое уравнение есть обыкновенное дифференциальное уравнение первого порядка, но второй степени. Разрешая его относительно y’x (предварительно разделив все члены уравнения на dx2), получим два уравнения:
|
| (1.4.101) |
|
| (1.4.102) |
(предполагается, что ас — b20 всюду в области G). Пусть общий интеграл уравнения (1.4.101) имеет вид
| (х, у)= k , | (1.4.111) |
а общий интеграл уравнения (1.4.102)
| (х, у)= k. | (1.4.112) |
Интегральные кривые характеристического уравнения (т. е. все кривые, входящие в семейства (1.4.111) и (1.4.112)) называются характеристиками заданного дифференциального уравнения (1.4.1). В связи с этим рассматриваемый метод упрощения уравнения (1.4.1) называется методом характеристик.
Семейства (1.4.111) и (1.4.112) можно рассматривать, как общие интегралы уравнения (1.4.8) (это уравнение распадается на два уравнения (1.4.101) и (1.4.102)).
Следовательно, согласно доказанной теореме, функции
z=(х, у) и z=(х, у)
являются решениями уравнения в частных производных (1.4.6).
Функции (х, у) и (х, у) независимы друг от друга (можно доказать, что их якобиан отличен от нуля, если ас- b2
Похожие работы
... . Однако полного выравнивания температур никогда не происходит, так как конвективный теплоперенос гораздо мощнее теплообмена. Относительный вклад теплообмена возрастает с уменьшением скорости потока. Квазистационарное распределение температуры в стволе скважины выше продуктивных пластов для потока жидкости описывается следующей приближенной формулой (Чекалюк Э.Б.) T(z) = То- Гг + ГВ (1 - е -т ) ...
... влияния – RТ и чистой воды – Rwдля некоторого момента времени 3.6. Выводы В нулевом и первом приближениях решена задача о температурном поле, вызванном закачкой радиоактивного раствора в глубокозалегающие пласты. На основании полученного решения установлены расчетные формулы для полей температуры, вызванных энергией распада и различием температур пласта и закачиваемой жидкости. ...

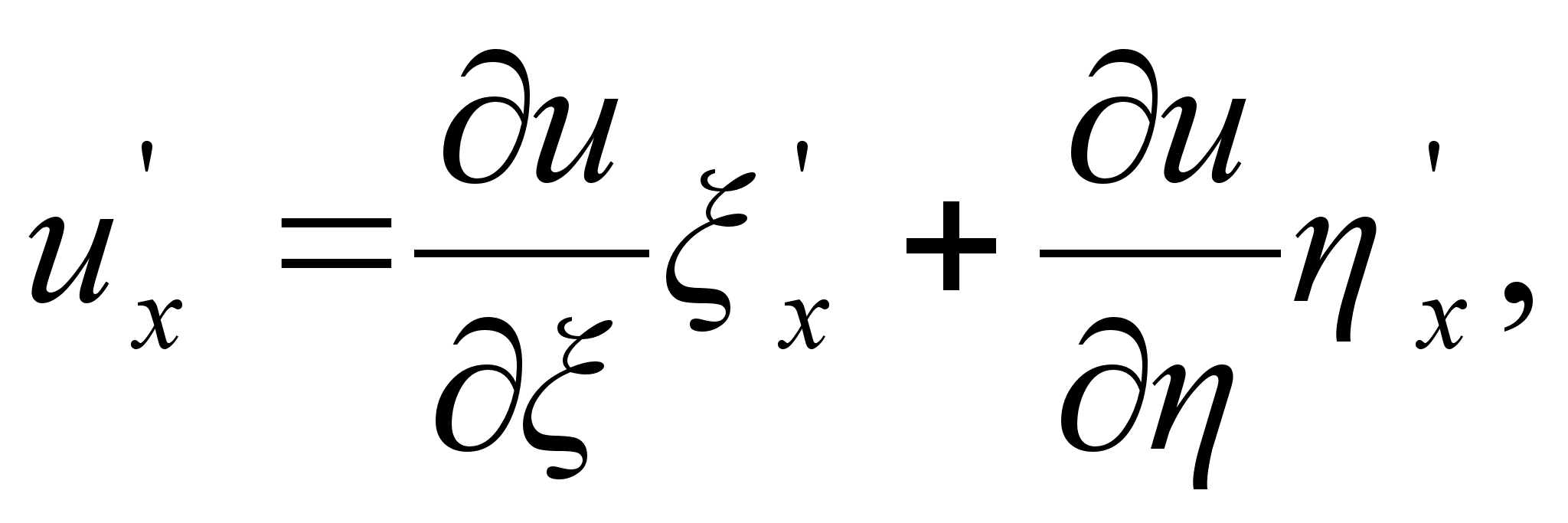


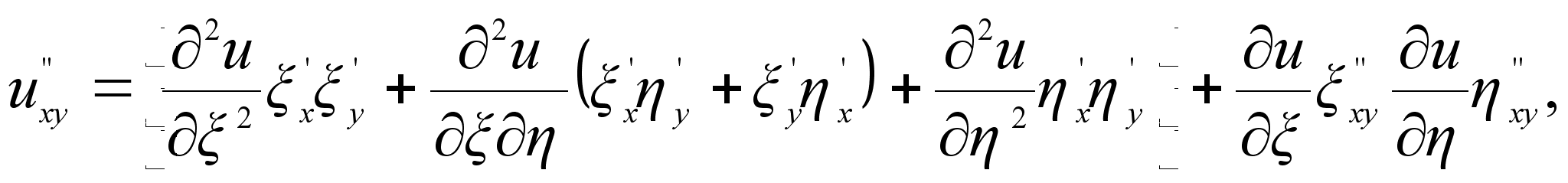

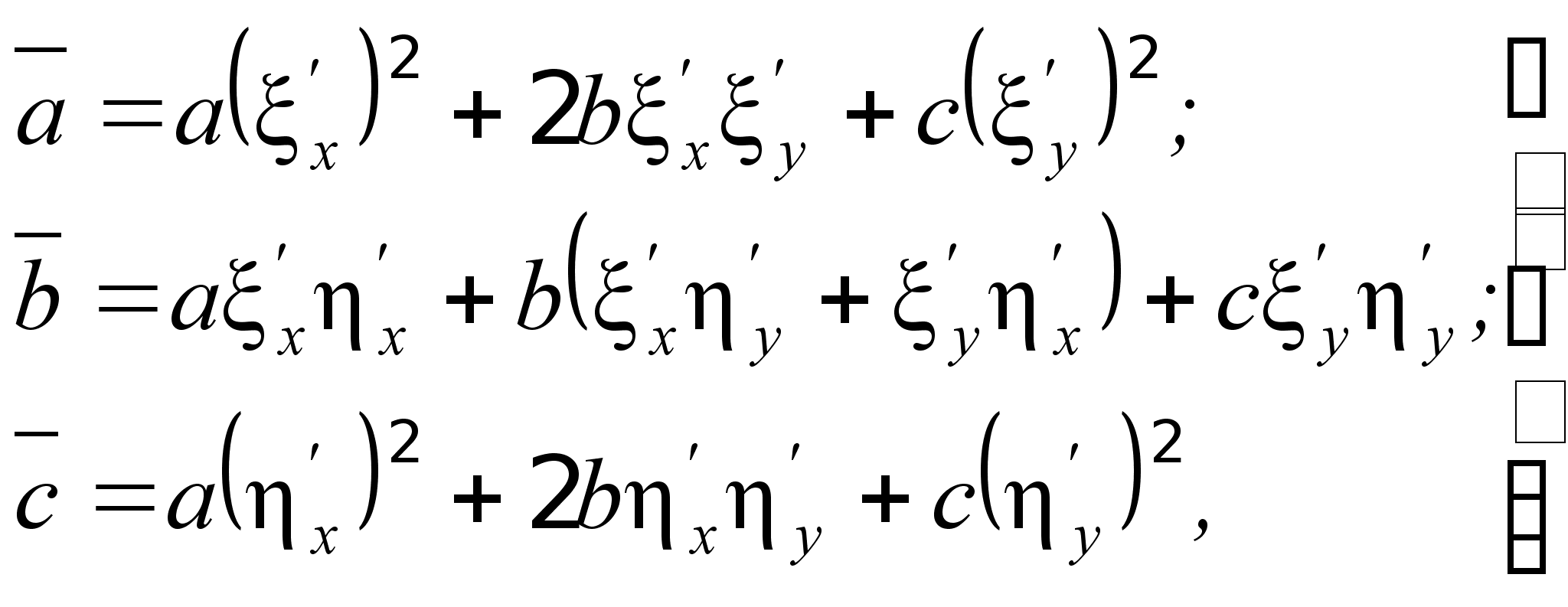
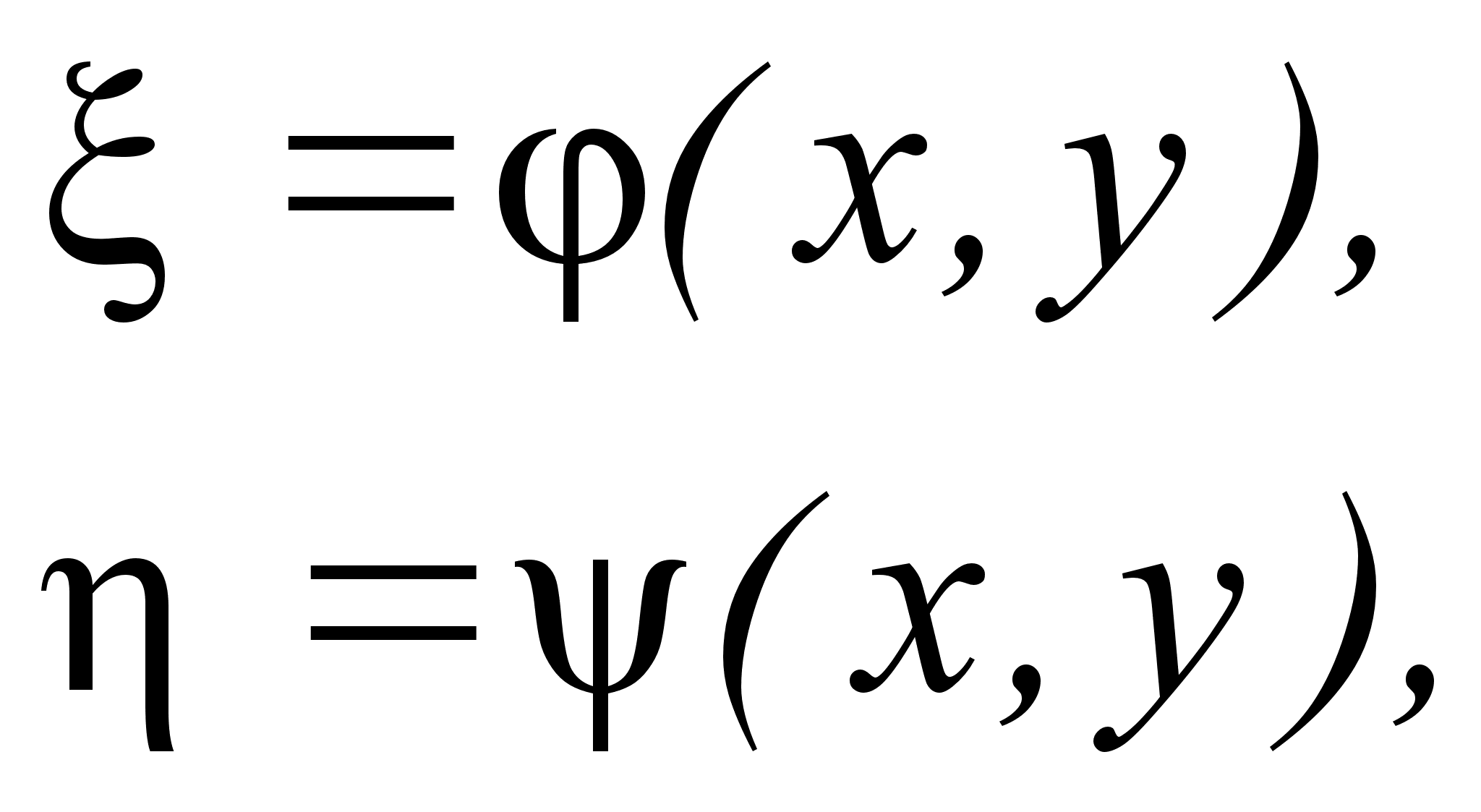
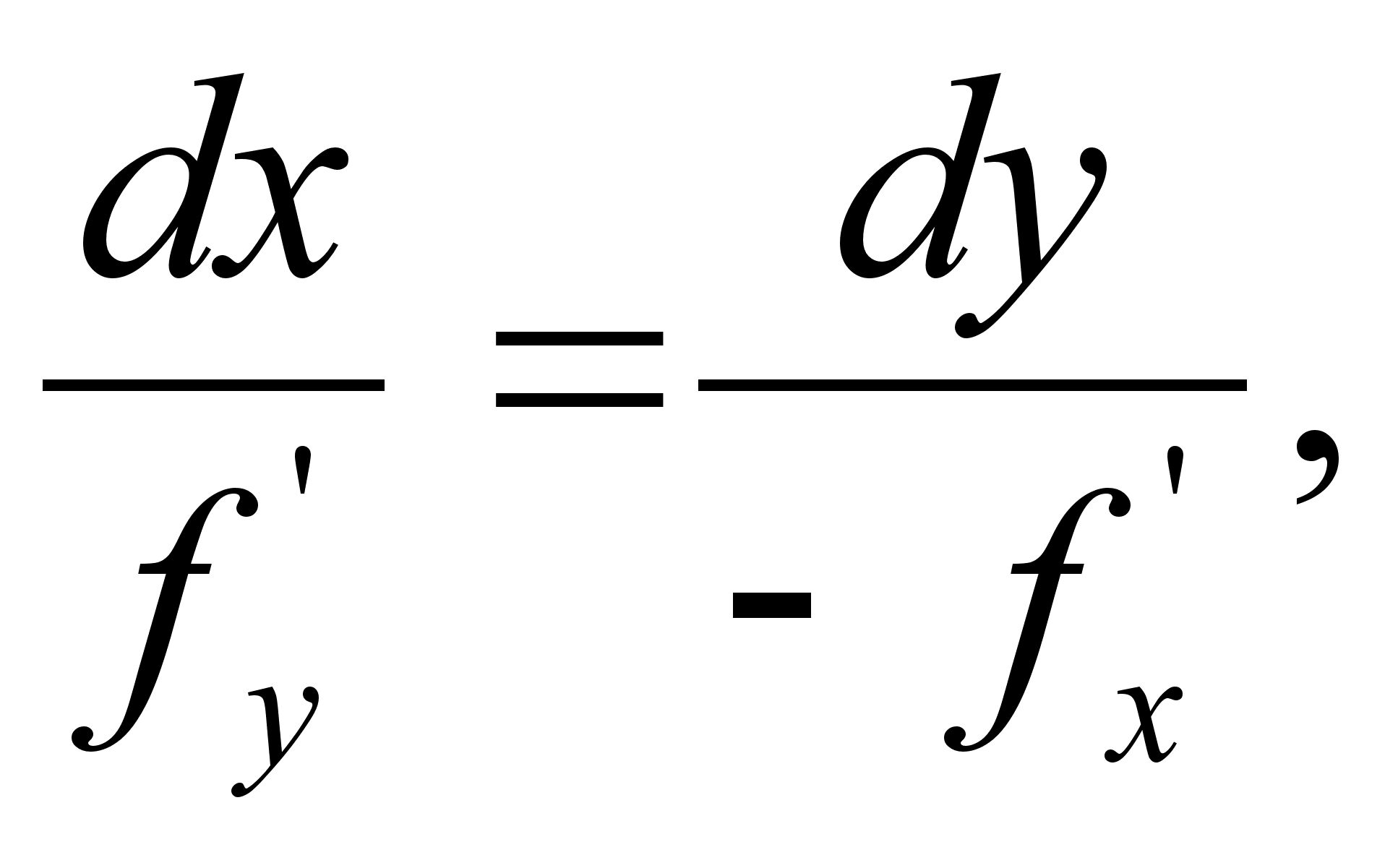


0 комментариев