Навигация
Импульс тела. 2. Закон сохранения импульса. 3. Применение закона сохранения импульса. 4. Реактивное движение
1. Импульс тела. 2. Закон сохранения импульса. 3. Применение закона сохранения импульса. 4. Реактивное движение.
Простые наблюдения и опыты доказывают, что покой и движение относительны, скорость тела зависит от выбора системы отсчета; по второму закону Ньютона, независимо от того, находилось ли тело в покое или двигалось, изменение скорости его движения может происходить только при действии силы, т. е. в результате взаимодействия с другими телами. Однако существуют величины, которые могут сохраняться при взаимодействии тел. Такими величинами являются энергия и импульс.
Импульсом тела называют векторную физическую величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Единица измерения импульса Р — кг • м/с. Импульс тела равен произведению массы тела на его скорость: р = mv. Направление вектора импульса р совпадает с направлением вектора скорости тела v (рис. 4).

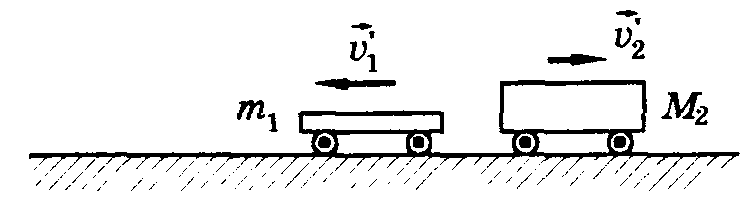
Рис. 4
Для импульса тел выполняется закон сохранения, который справедлив только для замкнутых физических систем. В общем случае замкнутой называют систему, которая не обменивается энергией и массой с телами и полями, не входящими в нее. В механике замкнутой называют систему, на которую не действуют внешние силы или действие этих сил скомпенсировано. В этом случае р1 = р2 где р1 — начальный импульс системы, а р2 — конечный. В случае двух тел, входящих в систему, это выражение имеет вид m1v1 + т2v2 = m1v1' + т2v2' где т1 и т2 — массы тел, а v1 и v2, — скорости до взаимодействия, v1' иv2' — скорости после взаимодействия. Эта формула и является математическим выражением закона сохранения импульса: импульс замкнутой физической системы сохраняется при любых взаимодействиях, происходящих внутри этой системы.
Другими словами: в замкнутой физической системе геометрическая сумма импульсов тел до взаимодействия равна геометрической сумме импульсов этих тел после взаимодействия. В случае незамкнутой системы импульс тел системы не сохраняется. Однако, если в системе существует направление, по которому внешние силы не действуют или их действие скомпенсировано, то сохраняется проекция импульса на это направление. Кроме того, если время взаимодействия мало (выстрел, взрыв, удар), то за это время даже в случае незамкнутой системы внешние силы незначительно изменяют импульсы взаимодействующих тел. Поэтому для практических расчетов в этом случае тоже можно применять закон сохранения импульса.
Экспериментальные исследования взаимодействий различных тел — от планет и звезд до атомов и элементарных частиц — показали, что в любой системе взаимодействующих тел при отсутствии действия со стороны других тел, не входящих в систему или равенстве нулю суммы действующих сил, геометрическая сумма импульсов тел действительно остается неизменной.
В механике закон сохранения импульса и законы Ньютона связаны между собой. Если на тело массой т в течение времени t действует сила и скорость его движения изменяется от v0 до v, то ускорение движения a тела равно a = (v - v0)/t. На основании второго закона Ньютона для силы F можно записать F = та = m(v - v0)/t, отсюда следует Ft = mv - mv0.
Ft — векторная физическая величина, характеризующая действие на тело силы за некоторый промежуток времени и равная произведению силы на время t ее действия, называется импульсом силы.
Единица импульса в СИ — Н • с.
Закон сохранения импульса лежит в основе реактивного движения. Реактивное движение — это такое движение тела, которое возникает после отделения от тела его части.
Пусть тело массой т покоилось. От тела отделилась какая-то его часть т1 со скоростью v1. Тогда
оставшаяся часть придет в движение в противоположную сторону со скоростью v2, масса оставшейся части т2 Действительно, сумма импульсов обоих частей тела до отделения была равна нулю и после разделения будет равна нулю:
т1v1 +m2v2 = 0, отсюда v1 = -m2v2/m1.
Большая заслуга в развитии теории реактивного движения принадлежит К. Э. Циолковскому.
Он разработал теорию полета тела переменной массы (ракеты) в однородном поле тяготения и рассчитал запасы топлива, необходимые для преодоления силы земного притяжения; основы теории жидкостного реактивного двигателя, а так же элементы его конструкции; теорию многоступенчатых ракет, причем предложил два варианта: параллельный (несколько реактивных двигателей работают одновременно) и последовательный (реактивные двигатели работают друг за другом). К. Э. Циолковский строго научно доказал возможность полета в космос с помощью ракет с жидкостным реактивным двигателем, предложил специальные траектории посадки космических аппаратов на Землю, выдвинул идею создания межпланетных орбитальных станций и подробно рассмотрел условия жизни и жизнеобеспечения на них. Технические идеи Циолковского находят применение при создании современной ракетно-космической техники. Движение с помощью реактивной струи, по закону сохранения импульса, лежит в основе гидрореактивного двигателя. В основе движения многих морских моллюсков (осьминогов, медуз, кальмаров, каракатиц) также лежит реактивный принцип.
Билет№4
Закон всемирного тяготения. Сила тяжести. Вес тела. Невесомость
План ответа
1. Силы гравитации. 2. Закон всемирного тяготения. 3. Физический смысл гравитационной постоянной. 4. Сила тяжести. 5. Вес тела, перегрузки. 6. Невесомость.
Исаак Ньютон выдвинул предположение, что между любыми телами в природе существуют силы взаимного притяжения. Эти силы называют силами гравитации, или силами всемирного тяготения. Сила всемирного тяготения проявляется в Космосе, Солнечной системе и на Земле. Ньютон обобщил законы движения небесных тел и выяснил, что F = G(m1*m2)/R2, где G — коэффициент пропорциональности, называется гравитационной постоянной. Численное значение гравитационной постоянной опытным путем определил Кавендиш, измеряя силу взаимодействия между свинцовыми шарами. В результате закон всемирного тяготения звучит так: между любыми материальными точками существует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними, действующая по линии, соединяющей эти точки.
Физический смысл гравитационной постоянной вытекает из закона всемирного тяготения. Если m1 = m2 = 1 кг, R = 1 м, то G = F, т. е. гравитационная постоянная равна силе, с которой притягиваются два тела по 1 кг на расстоянии 1 м. Численное значение: G = 6,67 • 10-11 Н • м2/кг2. Силы всемирного тяготения действуют между любыми телами в природе, но ощутимыми они становятся при больших массах (или хотя бы масса одного из тел велика). Закон же всемирного тяготения выполняется только для материальных точек и шаров (в этом случае за расстояние принимается расстояние между центрами шаров).
Ч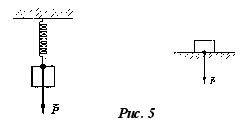 астным
видом силы
всемирного
тяготения
является сила
притяжения
тел к Земле
(или к другой
планете). Эту
силу называют
силой тяжести.
Под действием
этой силы все
тела приобретают
ускорение
свободного
падения. В
соответствии
со вторым законом
Ньютона
g
= fт/m,
следовательно,
fт
= mg.
Сила
тяжести
всегда направлена
к центру Земли.
В зависимости
от высоты
h
над поверхностью
Земли и географической
широты положения
тела ускорение
свободного
падения приобретает
различные
значения. На
поверхности
Земли и в средних
широтах ускорение
свободного
падения равно
9,831 м/с2.
астным
видом силы
всемирного
тяготения
является сила
притяжения
тел к Земле
(или к другой
планете). Эту
силу называют
силой тяжести.
Под действием
этой силы все
тела приобретают
ускорение
свободного
падения. В
соответствии
со вторым законом
Ньютона
g
= fт/m,
следовательно,
fт
= mg.
Сила
тяжести
всегда направлена
к центру Земли.
В зависимости
от высоты
h
над поверхностью
Земли и географической
широты положения
тела ускорение
свободного
падения приобретает
различные
значения. На
поверхности
Земли и в средних
широтах ускорение
свободного
падения равно
9,831 м/с2.
В технике и быту широко используется понятие веса тела. Весом тела называют силу, с которой тело давит на опору или подвес в результате гравитационного притяжения к планете (рис. 5). Вес тела обозначается Р. Единица измерения веса — 1 Н. Так как вес равен силе, с которой тело действует на опору, то в соответствии с третьим законом Ньютона по величине вес тела равен силе реакции опоры. Поэтому, чтобы найти вес тела, необходимо найти, чему равна сила реакции опоры.
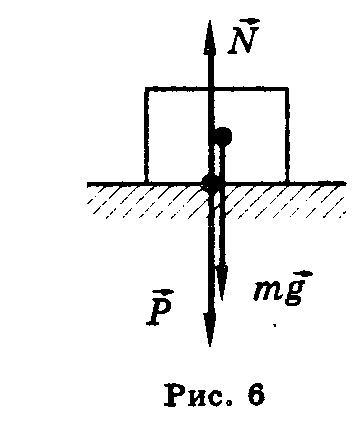
Рассмотрим случай, когда тело вместе с опорой не движется. В этом случае сила реакции опоры, а следовательно, и вес тела равен силе тяжести (рис. 6):р = N = mg.
 В
случае движения
тела вертикально
вверх вместе
с опорой с
ускорением,
по второму
закону Ньютона,
можно записать
mg
+ N = та
(рис. 7, а).
В
случае движения
тела вертикально
вверх вместе
с опорой с
ускорением,
по второму
закону Ньютона,
можно записать
mg
+ N = та
(рис. 7, а).
В проекции на ось OX: -mg + N = та, отсюда N = m(g + а).
Следовательно, при движении вертикально вверх с ускорением вес тела увеличивается и находится по формуле Р = m(g + а).
Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают на себе космонавты как при взлете космической ракеты, так и при торможении корабля при входе в плотные слои атмосферы. Испытывают перегрузки и летчики при выполнении фигур высшего пилотажа, и водители автомобилей при резком торможении.
Если тело движется Вниз по вертикали, то с помощью аналогичных рассуждений получаем mg +
+N = та; mg -N = та; N = m(g -а); Р = m(g - а), т. е. вес при движении по вертикали с ускорением будет меньше силы тяжести.
Если тело свободно падает, в этом случае Р = (g - g)m = 0.
Состояние тела, в котором его вес равен нулю, называют невесомостью. Состояние невесомости наблюдается в самолете или космическом корабле при движении с ускорением свободного падения независимо от направления и значения скорости их движения. За пределами земной атмосферы при выключении реактивных двигателей на космический корабль действует только сила всемирного тяготения. Под действием этой силы космический корабль и все тела, находящиеся в нем, движутся с одинаковым ускорением, поэтому в корабле наблюдается состояние невесомости.
Билет5
Превращение энергии при механических колебаниях. Свободные и вынужденные колебания. Резонанс
План ответа
Похожие работы
... в широкую практику разработки программ объектно-ориентированного программирования, впитавшего в себя идеи структурного и модульного программирования, структурное программирование стало фактом истории информатики. Билет № 9 Текстовый редактор, назначение и основные функции. Для работы с текстами на компьютере используются программные средства, называемые текстовыми редакторами или текстовыми ...
... признаков в популяции Задачи генетики: 1. В области с/х - выведение новых сортов растений и новых пород животных, а также усовершенствование существующих 2. Медицинская генетика - разработка методов диагностики неследственных заболеваний, разработка их профилактики 3. Генная инженерия 43. Особенности наследования при моногибридном скрещивании, установленные Г.Менделем. ...
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
... могут быть данные различных типов (целые или вещественные числа, строки, логические значения). Соответственно переменные бывают различных типов: целочисленные (А%=5), вещественные (А=3.14), строковые (А$="информатика'1), логические (A=True). Массивы являются набором однотипных переменных, объединенных одним именем. Массивы бывают одномерные, которые можно представить как одномерные ...

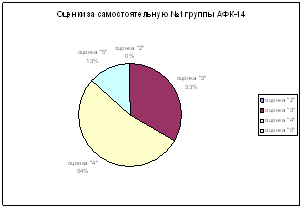

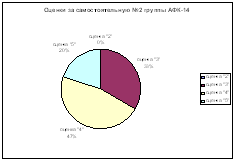
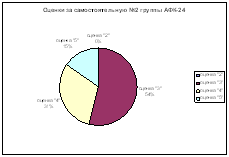

0 комментариев