Определение колебательного движения. 2. Свободные колебания. 3. Превращения энергии. 4. Вынужденные колебания

1. Определение колебательного движения. 2. Свободные колебания. 3. Превращения энергии. 4. Вынужденные колебания.

М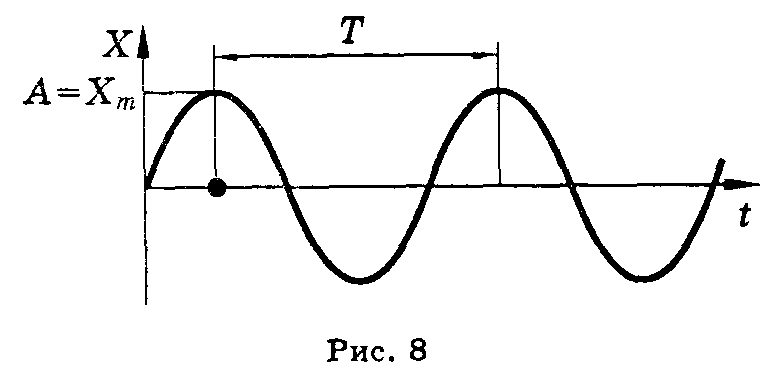еханическими колебаниями называют дви­жения тела, повторяющиеся точно или приблизи­тельно через одинаковые промежутки времени. Основ­ными характеристиками механических колебаний являются: смещение, амплитуда, частота, период. Смещение — это отклонение от положения равнове­сия. Амплитуда — модуль максимального отклоне­ния от положения равновесия. Частота — число полных колебаний, совершаемых в единицу времени. Период — время одного полного колебания, т. е. ми­нимальный промежуток времени, через который происходит повторение процесса. Период и частота связаны соотношением: v = 1/T.

Простейший вид колебательного движения — гармонические колебания, при которых колеблю­щаяся величина изменяется со временем по закону синуса или косинуса (рис. 8).

С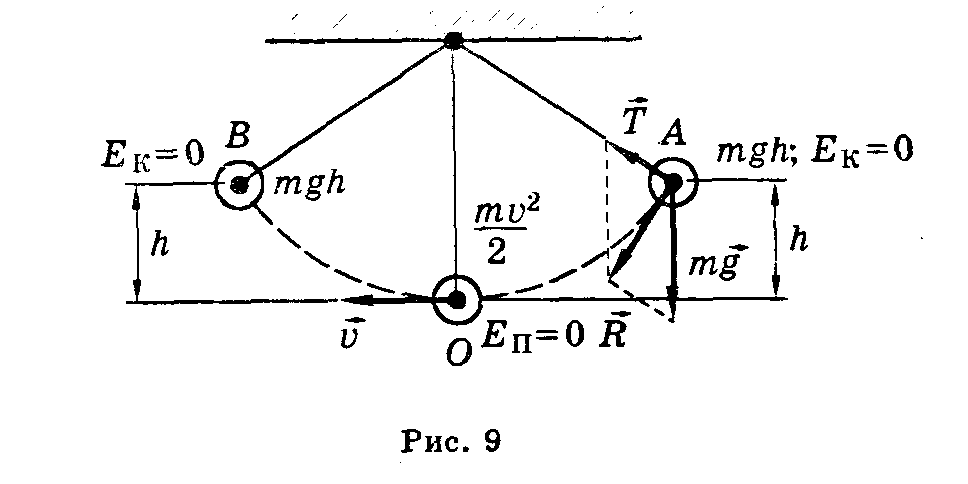вободными — называют колебания, которые совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воз­действий на систему, совершающую колебания. На­пример, колебания груза на нити (рис. 9).

Рассмотрим процесс превращения энергии на примере колебаний груза на нити (см. рис. 9).

При отклонении маятника от положения рав­новесия он поднимается на высоту h относительно нулевого уровня, следовательно, в точке А маятник обладает потенциальной энергией mgh. При движе­нии к положению равновесия, к точке О, уменьшает­ся высота до нуля, а скорость груза увеличивается, и в точке О вся потенциальная энергия mgh превратит­ся в кинетическую энергию mv^г/2. В положении равновесия кинетическая энергия имеет максималь­ное значение, а потенциальная энергия минимальна. После прохождения положения равновесия происхо­дит превращение кинетической энергии в потенци­альную, скорость маятника уменьшается и при мак­симальном отклонении от положения равновесия становится равной нулю. При колебательном движе­нии всегда происходят периодические превращения его кинетической и потенциальной энергий.

При свободных механических колебаниях не­избежно происходит потеря энергии на преодоление сил сопротивления. Если колебания происходят под действием периодически действующей внешней си­лы, то такие колебания называют вынужденными. Например, родители раскачивают ребенка на каче­лях, поршень движется в цилиндре двигателя авто­мобиля, колеблются нож электробритвы и игла швейной машины. Характер вынужденных колеба­ний зависит от характера действия внешней силы, от ее величины, направления, частоты действия и не зависит от размеров и свойств колеблющегося тела. Например, фундамент мотора, на котором он закреп­лен, совершает вынужденные колебания с частотой, определяемой только числом оборотов мотора, и не зависит от размеров фундамента.

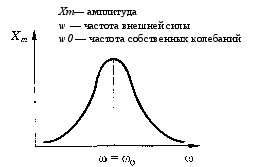
При совпадении частоты внешней силы и час­тоты собственных колебаний тела амплитуда вынуж­денных колебаний резко возрастает. Такое явление называют механическим резонансом. Графически за­висимость вынужденных колебаний от частоты дей­ствия внешней силы показана на рисунке 10.

Явление резонанса может быть причиной раз­рушения машин, зданий, мостов, если собственные их частоты совпадают с частотой периодически дей­ствующей силы. Поэтому, например, двигатели в ав­томобилях устанавливают на специальных амортиза­торах, а воинским подразделениям при движении по мосту запрещается идти «в ногу».

При отсутствии трения амплитуда вынужден­ных колебаний при резонансе должна возрастать со временем неограниченно. В реальных системах ам­плитуда в установившемся режиме резонанса опре­деляется условием потерь энергии в течение периода и работы внешней силы за то же время. Чем меньше трение, тем больше амплитуда при резонансе.

Билет №6

Опытное обоснование основных положений МКТ строения вещества. Масса и размер молекул. Постоянная Авогадро

План ответа

1. Основные положения. 2. Опытные доказа­тельства. 3. Микрохарактеристики вещества.

Молекулярно-кинетическая теория — это раз­дел физики, изучающий свойства различных состоя­ний вещества, основывающийся на представлениях о существовании молекул и атомов, как мельчайших частиц вещества. В основе МКТ лежат три основных положения:

1. Все вещества состоят из мельчайших час­тиц: молекул, атомов или ионов.

2. Эти частицы находятся в непрерывном хао­тическом движении, скорость которого определяет температуру вещества.

3. Между частицами существуют силы притя­жения и отталкивания, характер которых зависит от расстояния между ними.

Основные положения МКТ подтверждаются многими опытными фактами. Существование моле­кул, атомов и ионов доказано экспериментально, мо­лекулы достаточно изучены и даже сфотографирова­ны с помощью электронных микроскопов. Способ­ность газов неограниченно расширяться и занимать весь предоставленный им объем объясняется непре­рывным хаотическим движением молекул. Упругость газов, твердых и жидких тел, способность жидкостей

смачивать некоторые твердые тела, процессы окра­шивания, склеивания, сохранения формы твердыми телами и многое другое говорят о существовании сил притяжения и отталкивания между молекулами. Явление диффузии — способность молекул одного вещества проникать в промежутки между молекула­ми другого — тоже подтверждает основные положе­ния МКТ. Явлением диффузии объясняется, напри­мер, распространение запахов, смешивание разно­родных жидкостей, процесс растворения твердых тел в жидкостях, сварка металлов путем их расплавле-ния или путем давления. Подтверждением непре­рывного хаотического движения молекул является также и броуновское движение — непрерывное хао­тическое движение микроскопических частиц, не­растворимых в жидкости.

Движение броуновских частиц объясняется хаотическим движением частиц жидкости, которые сталкиваются с микроскопическими частицами и приводят их в движение. Опытным путем было дока­зано, что скорость броуновских частиц зависит от температуры жидкости. Теорию броуновского движе­ния разработал А. Эйнштейн. Законы движения час­тиц носят статистический, вероятностный характер. Известен только один способ уменьшения интенсив­ности броуновского движения — уменьшение темпе­ратуры. Существование броуновского движения убе­дительно подтверждает движение молекул.

Любое вещество состоит из частиц, поэтому количество вещества принято считать пропорцио­нальным числу частиц, т. е. структурных элементов, содержащихся в теле, v.

Единицей количества вещества является моль. Моль — это количество вещества, содержащее столько же структурных элементов любого вещества, сколько содержится атомов в 12 г углерода С¹². От­ношение числа молекул вещества к количеству ве­щества называют постоянной Авогадро:

n_a = N/v. na = 6,02 • 10²³ моль^-1.

Постоянная Авогадро показывает, сколько ато­мов и молекул содержится в одном моле вещества. Мо­лярной массой называют величину, равную отноше­нию массы вещества к количеству вещества:

М = m/v.

Молярная масса выражается в кг/моль. Зная молярную массу, можно вычислить массу одной мо­лекулы:

m₀ = m/N = m/vN_A = М/N_A

Средняя масса молекул обычно определяется химическими методами, постоянная Авогадро с вы­сокой точностью определена несколькими физиче­скими методами. Массы молекул и атомов со значи­тельной степенью точности определяются с помощью масс-спектрографа.

Массы молекул очень малы. Например, масса молекулы воды: т = 29,9 •10 ^-27 кг.

Молярная масса связана с относительной мо­лекулярной массой Mr. Относительная молярная масса — это величина, равная отношению массы мо­лекулы данного вещества к 1/12 массы атома угле­рода С¹². Если известна химическая формула вещест­ва, то с помощью таблицы Менделеева может быть определена его относительная масса, которая, будучи выражена в килограммах, показывает величину мо­лярной массы этого вещества.

Диаметром молекулы принято считать мини­мальное расстояние, на которое им позволяют сбли­зиться силы отталкивания. Однако понятие размера молекулы является условным. Средний размер моле­кул порядка 10^-10 м.

Билет №7

Идеальный газ. Основное уравнение МКТ идеального газа. Температура и ее измерение. Абсолютная температура

План ответа

1. Понятие идеального газа, свойства. 2. Объ­яснение давления газа. 3. Необходимость измерения температуры. 4. Физический смысл температуры. 5. Температурные шкалы. 6. Абсолютная темпера­тура.

Для объяснения свойств вещества в газообраз­ном состоянии используется модель идеального газа. Идеальным принято считать газ, если:

а) между мо­лекулами отсутствуют силы притяжения, т. е. моле­кулы ведут себя как абсолютно упругие тела;

б) газ очень разряжен, т. е. расстояние между молекулами намного больше размеров самих молекул;

в) тепловое равновесие по всему объему достигается мгновенно. Условия, необходимые для того, чтобы реальный газ обрел свойства идеального, осуществляются при со­ответствующем разряжении реального газа. Некото­рые газы даже при комнатной температуре и атмо­сферном давлении слабо отличаются от идеальных.

Основными параметрами идеального газа являются давление, объем и температура.

Одним из первых и важных успехов МКТ было качественное и количественное объяснение давления газа на стенки сосуда. Качественное объяснение за­ключается в том, что молекулы газа при столкнове­ниях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела и передают свои импульсы стенкам сосуда.

На основании использования основных поло­жений молекулярно-кинетической теории было по­лучено основное уравнение МКТ идеального газа, ко­торое выглядит так: р = 1/3 т₀пv².

Здесь р — давление идеального газа, m₀ —

масса молекулы, п — концентрация молекул, v² — средний квадрат скорости молекул.

Обозначив среднее значение кинетической энергии поступательного движения молекул идеаль­ного газа Е_k получим основное уравнение МКТ иде­ального газа в виде: р = 2/3nЕ_k.

Однако, измерив только давление газа, невоз­можно узнать ни среднее значение кинетической энергии молекул в отдельности, ни их концентра­цию. Следовательно, для нахождения микроскопиче­ских параметров газа нужно измерение какой-то еще физической величины, связанной со средней кинети­ческой энергией молекул. Такой величиной в физике является температура. Температура — скалярная физическая величина, описывающая состояние тер­модинамического равновесия (состояния, при кото­ром не происходит изменения микроскопических па­раметров). Как термодинамическая величина температура характеризует тепловое состояние системы и измеряется степенью его отклонения от принятого за нулевое, как молекулярно-кинетическая величина характеризует интенсивность хаотического движения молекул и измеряется их средней кинетической энергией.

E_k = 3/2 kT, где k = 1,38 • 10^-23 Дж/К и назы­вается постоянной Больцмана.

Температура всех частей изолированной си­стемы, находящейся в равновесии, одинакова. Изме­ряется температура термометрами в градусах раз­личных температурных шкал. Существует абсолют­ная термодинамическая шкала (шкала Кельвина) и различные эмпирические шкалы, которые отличают­ся начальными точками. До введения абсолютной шкалы температур в практике широкое распростра­нение получила шкала Цельсия (за О °С принята точка замерзания воды, за 100 °С принята точка ки­пения воды при нормальном атмосферном давлении).

Единица температуры по абсолютной шкале называется Кельвином и выбрана равной одному гра­дусу по шкале Цельсия 1 К = 1 °С. В шкале Кельви­на за ноль принят абсолютный ноль температур, т. е. температура, при которой давление идеального газа при постоянном объеме равно нулю. Вычисления да­ют результат, что абсолютный ноль температуры ра­вен -273 °С. Таким образом, между абсолютной шкалой температур и шкалой Цельсия существует связь Т = t °С + 273. Абсолютный ноль температур недостижим, так как любое охлаждение основано на испарении молекул с поверхности, а при приближе­нии к абсолютному нулю скорость поступательного движения молекул настолько замедляется, что испарение практически прекращается. Теоретически при абсолютном нуле скорость поступательного движения молекул равна нулю, т. е. прекращается тепловое движение молекул.

Билет №8

Уравнение состояния идеального газа. (Уравнение Менделеева—Клапейрона.) Изопропессы

План ответа

Похожие работы

Экзаменационные билеты по информатике 2000/2001 учебный год

Скачать

177159

29

21

... в широкую практику разработки программ объектно-ориентированного программирования, впитавшего в себя идеи структурного и модульного программирования, структурное программирование стало фактом истории информатики. Билет № 9 Текстовый редактор, назначение и основные функции. Для работы с текстами на компьютере используются программные средства, называемые текстовыми редакторами или текстовыми ...

Ответы на экзаменационные билеты по биологии за 11 класс медицинского лицея

Скачать

91327

1

0

... признаков в популяции   Задачи генетики: 1.   В области с/х - выведение новых сортов растений и новых пород животных, а также усовершенствование существующих 2.   Медицинская генетика - разработка методов диагностики неследственных заболеваний, разработка их профилактики 3.   Генная инженерия 43. Особенности наследования при моногибридном скрещивании, установленные Г.Менделем. ...

Организация и содержание элективного курса "Основы теории вероятностей и математической статистики" в классах оборонно-спортивного профиля

Скачать

138817

24

10

... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1.  Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...

Ответы к экзаменационным билетам по Информатике. 2001-2002 год

Скачать

132621

8

0

... могут быть данные различных типов (целые или вещественные числа, строки, логи­ческие значения). Соответственно переменные бывают различных типов: целочисленные (А%=5), веществен­ные (А=3.14), строковые (А$="информатика'1), логиче­ские (A=True). Массивы являются набором однотипных перемен­ных, объединенных одним именем. Массивы бывают одномерные, которые можно представить как одномер­ные ...