Устойчивое и неустойчивое состояния

1.4. Устойчивое и неустойчивое состояния

Когда ВАХ имеет падающий характер, нагрузочная прямая зачастую пересекает ее не в одной, а в двух точках (рис.5). Одно из состояний, а именно верхнее, является неустойчивым и поэтому не реализуется. В самом деле, если по какой-то причине ток случайно повышается, для его поддержания достаточно будет меньшего напряжения, чем фактическое, которое при данных ЭДС и внешнем сопротивлении непременно соответствует нагрузочной прямой.

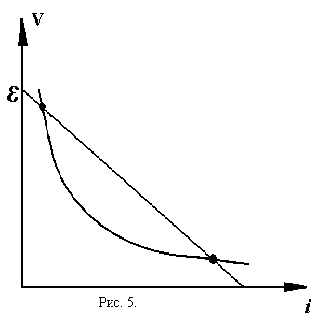
Возникнет дисбаланс между ионизацией и гибелью электронов, ионизация начнет расти, сопротивление разряда падать, ток расти, пока состояние не достигнет нижней точки пересечения. Нижнее состояние устойчиво. При n_e>0, i>0 напряжение станет меньше необходимого и повышенная гибель вернет степень ионизации в исходное состояние.

Опыт показывает, что разряд редко сохраняет диффузную форму, если газ в нем нагревается заметным образом, скажем вдвое, происходит контракция - стягивание столба в шнур, где степень ионизации, плотность тока и газовая температура резко повышаются - это преддверие к переходу тлеющего разряда в дугу при еще больших токах. Приведенные масштабы характеризуют верхние границы реализации слабоионизированной холодной плазмы диффузного тлеющего разряда. Чем выше давление, тем ниже по току и плотности электронов эта верхняя граница, тем сильнее нагревается газ при данном токе. Значит, для осуществления неравновесной слабоионизированной плазмы благоприятны низкие давления, для осуществления равновесной - высокие, порядка атмосферного.

Однородное состояние положительного столба тлеющего разряда часто оказывается неустойчивым, в особенности когда разряд происходит в больших объемах при повышенных давлениях, когда сильны ток и выделение джоулева тепла. Случайные возмущения катастрофически нарастают и плазма переходит в иное, пространственно неоднородное состояние. Вызываемые неустойчивостями неоднородные формации страты - разбиение положительного столба вдоль тока на чередующиеся светлые и темные слои [16]; контракция - стягивание плазмы в ярко светящийся токовый шнур известны давно [17,18]. Но в последнее время эти эффекты стали объектом особого внимания из-за тех затруднений, которые они вносят в создание мощных газовых лазеров. Преодоление тенденции к шнурованию разряда вылилось в центральную и самую трудную проблему при создании мощных электроразрядных лазеров.

Феноменологический признак устойчивости или неустойчивости

Неоднородность плазмы нередко видна на глаз. Неодинаковость свечения вызывается в первую очередь неодинаковостью плотности электронов. Стали быть, причины, приводящие к неоднородности, связаны с процессами, которые управляют плотностью электронов, их рождением, гибелью, переносом в пространстве.

Стационарному состоянию отвечает равенство скоростей и рождения и гибели Z₊=Z_- . Точке пересечения функций Z₊(n_e) и Z_-(n_e) соответствует стационарная плотность электронов n_e⁽⁰⁾, которая в конечном счете определяется внешними условиями: ЭДС источника, геометрией, более непосредственно - величиной тока, пропускаемого через разряд.

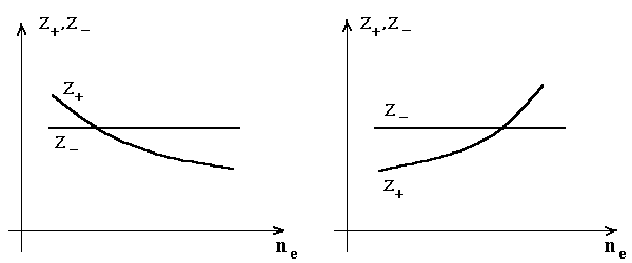
Рис. 6 а. Рис. 6 б.

Об устойчивости стационарного состояния можно судить по взаимному расположению кривых в его окрестности. Если при n_e>n_e⁽⁰⁾ Z_- проходит выше, а при n_e0 возмущения будут нарастать по экспоненциальному закону. Характерное время развития неустойчивости . Если  , возмущения затухают, то есть состояние устойчиво.

Рассасывание объемного заряда = n₊ - n_e - n_- в среде с постоянной проводимостью  определяется

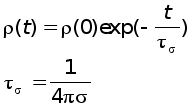
_ время исчезновения объемного заряда.

Давление выравнивается в пространстве со скоростью звука с. Электронная теплопроводность в слабо ионизированном газе kn_eD_e; соответствующая температуропроводность _e=D_e .

1.6. Механизмы неустойчивостей

Ионизационно-перегревная неустойчивость.

Приводит к контракции разряда, образованию токовых шнуров, в которых степень ионизации и температура газа резко повышены по сравнению с тлеющим разрядом. Развивается неустойчивость из поперечных неоднородностей, когда Е остается однородным вдоль направления тока.

Механизм неустойчивости отражается следующей замкнутой цепочкой причинных связей

Скорость нарастания возмущений лимитируется нагреванием газа.

Прилипательная неустойчивость.

Возникает при неслишком больших (n_e max [6D_a/_r , T₀/eEv_eb].

Примечательно, что из этого выражения следует ограничение на ток, J_max, который может протекать в неконтрагированном тлеющем разряде. Действительно, полный ток разряда записывается в виде

J = en_e_eER².

При пропускании большего тока либо за счет увеличения плотности плазмы, либо при переходе к трубкам с большим радиусом тлеющий разряд контрагирует. Таким образом, тепловая контракция является принципиальным физическим явлением, ограничивающим ток однородного тлеющего разряда в цилиндрических трубках.

Особенности контракции тлеющего разряда в молекулярных газах

Особенности разряда в молекулярных газах определяются в первую очередь тем, что у молекул есть низколежащие энергетические уровни, соответствующие внутримолекулярным колебаниям. Энергия колебательного кванта ~0.1 эВ, так что при значениях температуры электронов, типичных для плазмы тлеющего разряда, значительная часть энергии, вводимой в разряд молекулярного газа, расходуется на возбуждение колебательных уровней молекул. Вероятность релаксации энергии внутримолекулярных колебаний в температуру газа (V, T-релаксация) весьма мала. Значения характерного времени V, T - релаксаци в молекулярном масштабе, естественной единицей которого является время свободного пробега молекул между столкновениями, достигают десятков и даже сотен тысяч единиц. Поэтому в довольно широком диапазоне изменения условий разряда молекулярный газ может находиться в неравновесном состоянии. В этом состоянии запас колебательной энергии молекул существенно превышает равновесное значение, соответствующее температуре газа, которая в свою очередь может быть близка к температуре стенок разрядной трубки. По этой причине вытеснение газа из приосевой зоны разряда, приводящее к тепловой контракции тлеющего разряда в трубках, в молекулярном газе будет не слишком большим, как в атомарном. Примечательно, что с ростом температуры газа скорость V, T - релаксации растет [22].

С другой стороны, известно, что если скорость выделения тепла в газовой среде является функцией, достаточно быстро растущей с температурой, а отвод тепла осуществляется за счет теплопроводности газа, то в среде при достижении определенного запаса энергии произойдет “тепловой взрыв”. В результате теплового взрыва в рассматриваемом случае вся энергия, запасенная в колебательных степенях свободы молекул, преобразуется в температуру газа, посе чего, естесвенно произойдет тепловая контракция тлеющего разряда. При описании этого явления потупают также, как при описании классического теплового взрыва [21], то есть ищут условие, при котором стационарное решение уравнений, описывающих распределение температуры газа в разрядной трубке будет невозможным.

Для установления условий контракции разряда в сильнонеравновесном молекулярном газе необходимо учитывать в энергетическом балансе плазмы кинетику обмена энергией между разными степенями свободы. Система уравнений, описывающих баланс поступательной и колебательной энергий:

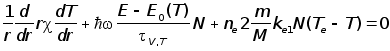(1)

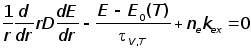(2)

где  - теплопроводность газа; D - коэффициент диффузии возбужденных молекул; N и n_e, M и m - концентрации и массы молекул и электронов соответственно; E(T) - среднее число колебательных квантов, приходящихся на одну молекулу; Е₀(Т) - равновесное значение, отвечающее темепратуре газа Т; - энергия колебательного кванта; _V,T -характерное время V, T - релаксации молекул; k_e1 - коэффициент упругого рассеяния электронов на молекуле; k_ex - коэффициент возбуждения колебательных уровней молекул; Т_е - температура электронов.

В уравнении теплопроводности (1), имеющем стандартные граничные условия, второе слагаемое описывает нагрев газа в результате V, T - релаксации молекул, а третье - нагрев газа за счет упругих электронно-молекулярных соударений.

В уравнениии баланса колебательной энергии (2) с граничными условиями

первое слагаемое описывает уход колебательно-возбужденных молекул на стенки трубки за счет диффузии, второе- процесс девозбуждения таких молекул в объеме разряда в результате V, T - релаксации, третье слагаемое описывает процесс образования колебательно-возбужденных молекул в результате электронно-молекулярных соударений.

Численные оценки [20] показывают, что рассмотренный механизм конракции разряда реализуется в таких газах, как, например, N₂ и CO при значениях NR>10¹⁷ см^-2. Это качественно согласуется с результатами экспериментальных исследований конракции разряда.

Устойчивость и характерные времена физических процессов

При соответствующей организации начальных условий можно реализовать в газе пространственно однородный стримерный пробой. Однако опыт показывает, что спустя некоторое время в объеме газоразрядной плазмы возникают сильные неоднородности, проявляющиеся в виде «шнуров» или страт. Это означает, что объемная низкотемпературная плазма газового разряда неустойчива по отношению к тем или иным пространственно неоднородным возмущениям. Естественно, что время развития этих неустойчивостей и определяет время горения объемных самостоятельных разрядов.

Стационарная процедура исследования на устойчивость однородного стационарного состояния некоторой системы, которое определяется параметрами n_e⁽⁰⁾, T⁽⁰⁾, N⁽⁰⁾ и др., заключается в том, что уравнения, описывающие поведение системы во времени и пространстве, линеаризуют, представляя все параметры в виде n_e(r, t) = n_e⁽⁰⁾ + n_e(r, t), . . . и считая отклонения от стационарного состояния малыми. Решение системы линейных уравнений для n_e(r, t), Т(r, t), . . . ищут в виде плоской волны:

n_e = (n_e)^(а)exp[i(t-kr)]

T = (T)^(а)exp[i(t-kr)], ...

Условием существования нетривиального решения системы однородных алгебраических уравнений, возникающей при подстановке приведенных выше выражений в уравнения для n_e(r, t), . . . , относительно амплитуд (n_e)^(а), . . . является равество нулю ее детерминанта, что и дает дисперсионное уравнение для определения . В общем случае это дисперсионное уравнение имеет комплексные корни, число которых равно числу параметров и уравнений. Если найдется хотя бы один корень, у которого Re(i)>0, малые отклонения от состояния равновесия будут нарастать с течением времени как exp(t). Величина , найденная с помощью линейной теории, характеризует инкремент развивающейся неустойчивости. Однако то, с какой точностью по значению этого инкремента можно определить полное время развития нейстойчивости, зависит от следующих обстоятельств.

Линейная теория развития неустойчивости предсказывает экспоненциальный закон роста флуктуаций, так что время, требуемое для усиления флуктуаций до некоторого минимального измеряемого уровня, зависит от начальной амплитуды возмущений. Поэтому чтобы определить, в какой степени величина =1/ характеризует полное время развития неустойчивости, необходимо, вообще говоря, рассматривать и нелинейную стадию роста флуктуаций. В случае, когда на нелинейной стадии своего развития неустойчивость развивается взрывным образом, величина =1/ дает полное время развития неустойчивости.

Кроме того, следует помнить, что каждая из рассматриваемых неустойчивостей может развиваться не из стационарного состояния, как это предполагается при использовании линейной теории развития возмущений, а на фоне нестационарности плазменных параметров объемного импульсного разряда. Поэтому линейная теория развития возмущений должна хорошо описывать реальную ситуацию, если характерное время изменения плазменных параметров, определяющих исследуемое на устойчивость состояние, превосходит время развития неустойчивости. Иными словами, исследуемое на устойчивость состояние является как бы «замороженным» по отношению к развивающимся процессам.

Анализ физических процессов и, соответственно, уравнений, которые описывают поведение низкотемпературной плазмы даже в простейшем молекулярном газе, показывает, что дисперсионное уравнение для определения (k) имеет по крайней мере десятый порядок. Хотя, конечно, численное решение всегда возможно, однако понять физическую суть явлений при этом крайне трудно.

Выход из столь непростого положения подсказывает оценка и сопоставление значений характерного времени для процессов, определяющих установление различных физических параметров. Дело в том, что в низкотемпературной плазме область значений характерных времен простирается от величины порядка 10^-12 с (характерное время релаксации объемного заряда) до величин порядка 10^-2 с (характерное время процесса переноса - диффузии, теплопроводности - в нейтральном газе). По этой причине при изучении неустойчивости неопределенного типа, связанной с действием какого-то главного для данных физических условий процесса и развивающейся за время , обычно удается отобрать как более быстрые процессы, которые протекают за время, гораздо меньшее, так и более медленные. Естественно, что быстро устанавливающиеся параметры можно считать квазистационарными, полагая, что они мгновенно «подстраиваются» к текущим значениям главных для данной физической ситуации параметров. Относительно более медленных процессов можно сказать, что за время развития неустойчивости данного типа соответствующие параметры вообще не успевают измениться и остаются «замороженными».

ПОСТАНОВКА ЗАДАЧИ

Исходя из вышеизложенного в данной дипломной работе поставлены следующие задачи:

исследовать влияние силы тока разряда на нормальную скорость горения;

исследование зависимости предельного значения тока разряда перехода диффузного разряда в шнуровой от состава горючей смеси;

теоретически исследовать устойчивость системы “пламя+разряд” по отношению к малым возмущениям температуры, плотности, концентрации заряженных частиц и так далее.

37

ОГЛАВЛЕНИЕ

Предисловие .........................................................................................................3

Введение ................................................................................................................4

Глава I. Обзор литературы. Постановка задачи ................................................6

Ионизация в зоне горения углеводородного топлива........................6

Диффузный электрический разряд ....................................................11

Положительный столб дуги высокого давления ..............................13

Устойчивое и неустойчивое состояния .............................................17

Инкремент нарастания неустойчивости ...........................................21

Механизмы неустойчивостей ............................................................22

Контракция положительного столба ...............................................22

Диффузионный режим горения тлеющего разряда в трубках ........24

Глава II. Экспериментальная установка и методика исследования ................33

Глава III. Анализ и обсуждение экспериментальных данных .........................36

3.1. Изучение воздействия электрического разряда на зону горения ....36

3.2. Расчет поля показателя преломления по интерферограмамм .........39

3.3. Теоретический анализ устойчивости системы “пламя+разряд” по отношению к малым возмущениям ..................................................46

Выводы ................................................................................................................52

Литература ..........................................................................................................53

Приложение ........................................................................................................55

ПРЕДИСЛОВИЕ

Автор дипломной работы выражает глубокую благодарность Станиславу Владимировичу Ильину и Владимиру Васильевичу Афанасьеву за постоянное внимание, поддержку и интерес к данной работе.

Автор также благодарит других сотрудников ПНИЛ “Физики неустойчивого горения” Николая Арсентьевича Тарасова и Александра Кириловича Кузьмина за помощь в работе.

ГЛАВА III

АНАЛИЗ И ОБСУЖДЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

В ходе экспериментов были получены: 1) прямая фотография процесса перехода диффузного электрического разряда в контрагированное состояние (см. рис. 14); 2) определены предельные токи шнурования разряда для пропано-воздушной смеси; 3) интерференционные снимки системы «пламя+разряд» в пропано-воздушной смеси; 4) фотографии системы «пламя+разряд» в пропано-кислородной смеси.

3.1.Изучение воздействия электрического разряда на зону горения углеводородных топлив.

В результате обработки экспериментальных данных были построены графики зависимости предельного тока шнурования от состава смеси (рис. 15), а также безразмерной высоты пламени (см. рис. 16) и нормальной скорости горения (рис. 17) от тока разряда при различных концентрациях пропана.

График зависимости относительного значения нормальной скорости горения от тока разряда представлен на рис. 17. Из него видно, что увеличение нормальной скорости горения происходит только до определенных значений тока разряда, т.е. наблюдается насыщение по току.

В работе также было исследовано влияние тока разряда на высоту пламени. Получен график зависимости относительного значения высоты пламени от тока разряда, который представлен на рис. 16. Из графика видно, что уменьшение высоты пламени происходит только до определенных значений тока разряда, т.е. также наблюдается насыщение по току. Полученные графические зависимости свидетельствуют о том, что режим насыщения наступает раньше в богатых смесях (при I=17 мА), потом в бедных (при I=19 мА) и потом в стехиометрических смесях (при I=25 мА).

В работе также определялись предельные значения токов шнурования диффузного разряда в зависимости от состава смеси. По экспериментальным данным построен график зависимости предельного значения тока перехода тлеющего разряда в дуговой от состава смеси (см рис.15). Из графика видно, что ток шнурования у стехиометрических смесей равен примерно 25 мА, у бедных - 19 мА, а у богатых - 17 мА. Следовательно, с увеличением содержания пропана в смеси шнурование происходит при меньших значениях тока

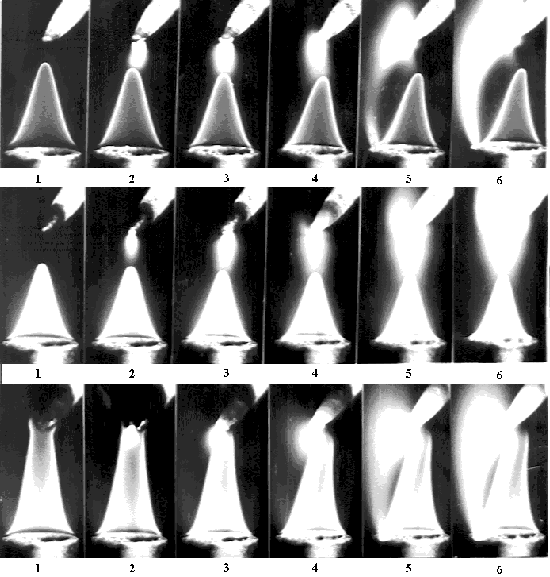
Рис. 14.

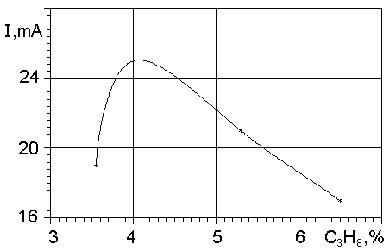
Рис. 15. Зависимость предельного значения тока перехода диффузного разряда в дуговой от состава пропано-бутано-воздушной смеси.

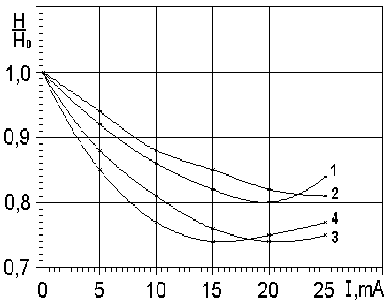
Рис.16. Зависимость относительного значения высоты пламени от тока разряда для различных составов горючей смеси.1-3,55% С₃Н₈; 2-4,1% С₃Н₈; 3-5,3% С₃Н₈; 4-6,5% С₃Н₈.

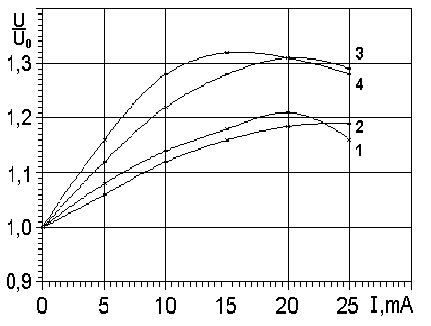
Рис. 17. Зависимость относительного значения нормальной скорости горения от силы тока разряда. 1- 3,55% С₃Н₈; 2 -4,1% С₃Н₈;3 -5,3% С₃Н₈; 4 -6,5%С₃Н₈.

Для пропано-кислородной смеси построены графики зависимостей безразмерной относительной высоты (см. рис. 18) и площади поверхности (см. рис. 19) пламени от тока (плотности тока) разряда. Все графики построены в GRAPHER.

3.2.Расчет поля показателя преломления по интреферограммам системы “пламя+разряд”.

По полученным интерферограммам были рассчитаны поля изменения показателя преломления, построены топограммы (см. рис. 20-30) для различных расходов и токов разряда. Для этих целей была написана компьютерная программа (см. приложение 1). Интерферограммы снимались на видеокамеру, после чего вводились в компьютер и оцифровывались программным продуктом ASYMETRICS DIGITAL VIDEO PRODUSER CAPTURE в графический файл формата bmp. Затем обрабатывались и оптимизировались пакетом FOTOFINISH. Топограммы строились с помощью программы SURFER.

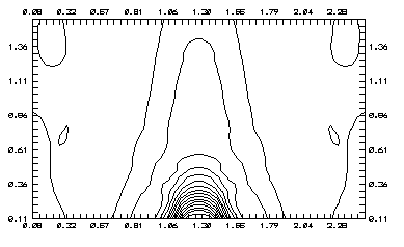
Рис. 20. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 2 см³/сек; воздух - 28 см³/сек. Без разряда

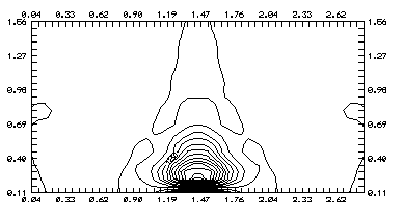
Рис. 21. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 2 см³/сек; воздух - 28 см³/сек. Разряд 5 mA.

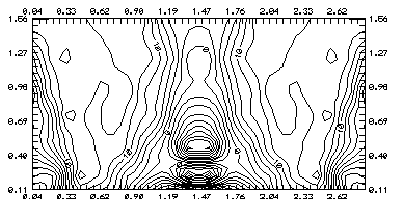
Рис. 22. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 3.8 см³/сек; воздух - 62 см³/сек. Без разряда

Рис. 23. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 3.8 см³/сек; воздух - 62 см³/сек. Разряд 10 mA.

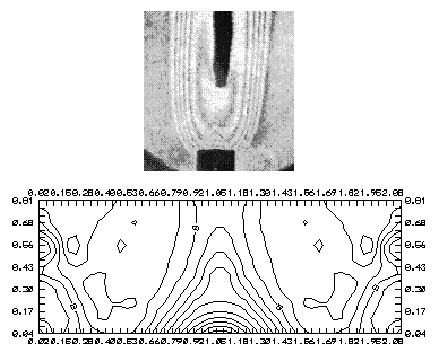
Рис. 24. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 1.3 см³/сек; воздух - 28 см³/сек. Без разряда.

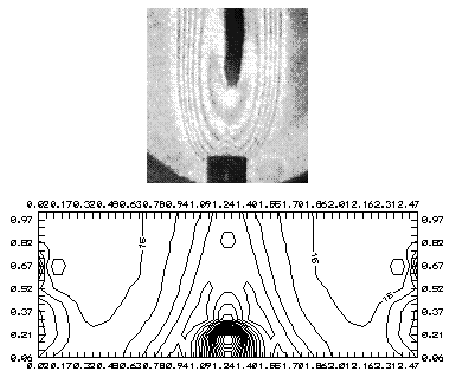
Рис. 25. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 1.3 см³/сек; воздух - 28 см³/сек. Разряд 5 mA.

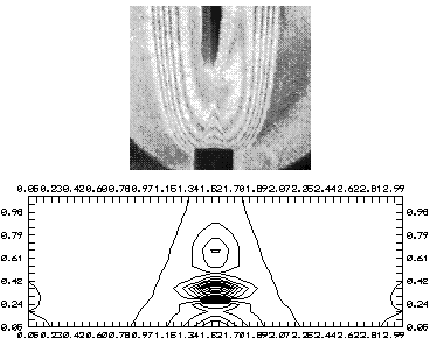
Рис. 26. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 3.2 см³/сек; воздух - 62 см³/сек. Без разряда.

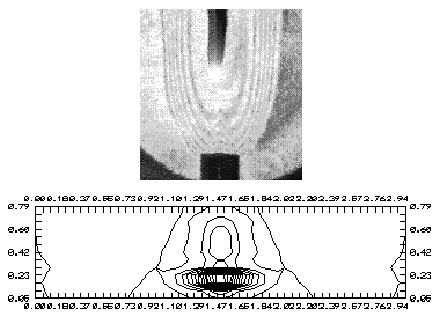
Рис. 27. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 3.2 см³/сек; воздух - 62 см³/сек. Разряд 10 mA.

Рис. 28. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 3.2 см³/сек; воздух - 62 см³/сек. Разряд 30 mA.

Рис. 29. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 2.7 см³/сек; воздух - 62 см³/сек. Без разряда.

Рис. 30. Смесь С₃Н₈ + воздух: расход С₃Н₈ - 2.7 см³/сек; воздух - 62 см³/сек. Разряд 30 mA.

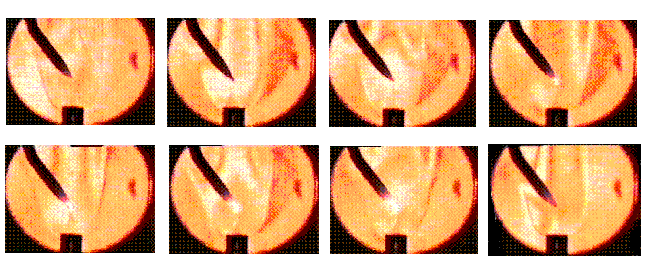
Рис. 31.

На рисунке 31 предсавлена серия фотографий, полученных методом двойной экспозиции относительно горящего пламени. Из этих сников видно, что в отсутствие разряда поверхность пламени не видна. В случае наложения разряда на пламя его поверхность сразу становится видимой. Это объясняется тем, что ток разряда идет по поверхности пламени и, следовательно, температура пламени повышается, в результате чего изменяется показатель преломления.

Для пропано-кислородной смеси была сделана попытка определить ток шнурования, но безуспешно. Для этого требуется более мощный источник питания. Если ток шнурования для пропано-воздушной смеси составлял ~ 25 mA, то для пропано-кислородной смеси он на порядок выше. По полученным данным построены графики зависимости безразмерной высоты пламени (рис. 32) и нормальной скорости горения (рис. 33) от тока (плотности тока) разряда.

Из сравнения результатов по воздуху и кислороду видно, что плотность тока для пропано-кислородной смеси на порядок больше.