Навигация
ЛАБОРАТОРНАЯ РАБОТА 1
СИНТЕЗ КОМБИНАЦИОННЫХ СХЕМ
1 Цель работы
Настоящая лабораторная работа знакомит студентов с основными логическими функциями и реализующими их элементами широко распространенной I55 серии интегральных микросхем, развивает навык в составлении уравнений, описывающих структуру логических устройств, их минимизации и реализации с учетом имеющегося набора логических элементов.
2 Краткая теория вопроса
2.1 Минимизация булевых функций
Для получения минимальной дизъюнктивной нормальной формы булевой функции воспользуемся методом карт Карно. Карты Карно позволяют достаточно быстро и эффективно минимизировать функции от малого числа (четыре - шесть) аргументов. При этом весьма просто минимизируются неполностью определённые функции. Такой класс функций наиболее часто встречается в проектировании простых узлов ЭВМ, в частности, узлов, синтезируемых на основе конечных автоматов.
Чтобы быстрее нанести булеву функцию, заданную таблично или алгебраически (СДНФ), рекомендуется следующий практический прием.
Основой будем считать карту Карно для четырех аргументов; из двух таких карт формируется карта для пяти аргументов, из четырех таких карт - карта Карно для шести аргументов. Так как аргументы являются переменными двоичного алфавита, то наборы аргументов можно рассматривать как целые двоичные числа.
Взаимное расположение аргументов должно быть чётко фиксированно, например, будем считать, что X1 - это первый разряд (младший), X2 - второй разряд, X3 - третий разряд, X4 - четвертый разряд и X5 - старший разряд. Четыре младших разряда определяют номер клетки внутри ос-
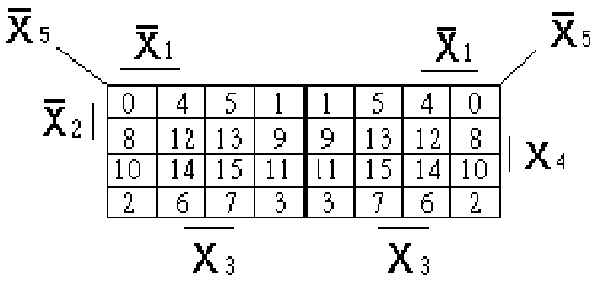
а) Карта Карно
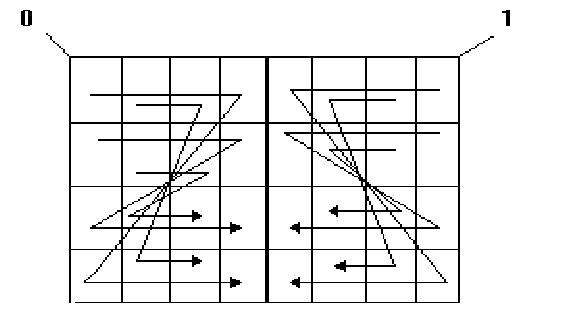
б) Карта Карно - “правило четырех Z”
Рисунок 1 - Карты Карно для пяти переменных
новной карты Карно, а пятый разряд задает номер такой карты (0 или 1). Если вместо двоичного кода воспользоваться десятичным эквивалентом, то номера наборов на карте Карно для пяти аргументов можно записать в виде изображённом на рисунке 1.а.
Расположение номеров наборов (клеток) в основной карте Карно легко запоминается по мнемоническому “правилу четырёх Z”. Это правило заключается в следующем: Z большое - это клетки 0,1,2,3; Z узкое - 4,5,6,7; Z широкое - 8,9,10,11; Z малое - 12,13,14,15.
В других картах принцип четырёх Z сохраняется, изменяются только направления и начальные точки (рисунок 1.б).
Если в таблице истинности отсутствуют некоторые строки, что соответствует неиспользованным кодам состояний (избыточное состояние) и запрещенным комбинациям входных сигналов, то в соответствующих клетках карты Карно ставятся прочерки или звёздочки.
На этих наборах (клетках) доопределяются значения функций так, чтобы получилась минимальная ДНФ булевой функции.
2.2 Пороговый элемент
Пороговым элементом называется логический элемент с n двоичными входами Xn , ... ,Xi , ... , X1 и одним выходом F, причем каждому входу Xi приписан некоторый “вес” Pi .
Сигнал на выходе порогового элемента принимает значение “1” только тогда , когда сумма весов входов , на которых сигнал имеет значение “1” (Xi =1), превосходит некоторый порог l. Таким образом, действие такого однопорогового элемента может быть описано функцией:
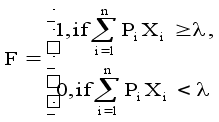
Структурой порогового элемента называется упорядоченный набор {Pn ,...,Pi ,...,P1 , l). При этом веса и порог могут быть любые действительные значения, однако будем считать их только целочисленными, как положительными, так и отрицательными. Логическая функция, которую реализует пороговый элемент, определяется только его структурой, т.е. значениями весов и порога.
Рассмотрим синтез порогового элемента.
Пример: Построить пороговый элемент в базисе И-НЕ со структурой {-2,1,3,2},т.е. веса P1=3,P2=1,P3=-2 , порог l=2 .
Решение: 1
этап. Построим
таблицу функционирования
такого элемента
с заданной
структурой.
Для этого нам
необходимо
заполнить
столбец суммы.
Значения суммы
мы найдем по
формуле
![]() PiXi.
PiXi.
Таблица 1 - Таблица
функционирования
| X3 -2 | X2 1 | X1 3 |
| F l=2 | |
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 3 | 1 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 4 | 1 | |
| 1 | 0 | 0 | -2 | 0 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | -1 | 0 | |
| 1 | 1 | 1 | 2 | 1 | |
2 этап.
Запишем СДНФ
полученной
функции F=![]() X2X1+X3X2X1
X2X1+X3X2X1
3 этап. После минимизации получим
F= X1
X2+
X1![]() =
X1(X2+
=
X1(X2+![]() )
)
4 этап. Приведем полученную функцию в базис И-НЕ
![]()
5 этап. Строим схему (рисунок 2).
Частным случаем порогового элемента является мажоритарный элемент с нечетным числом n входов.
2.3 Мажоритарный элемент
Мажоритарным элементом называют логический элемент, работающий по принципу большинства. Принцип большинства
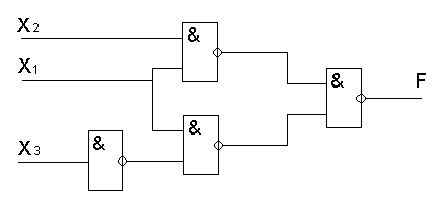
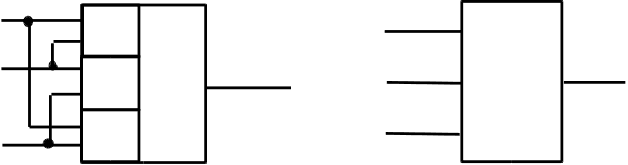
Рисунок 2 - Пороговый элемент
заключается в том, что если большинство входных сигналов равно 1 или 0, то и выходной сигнал будет соответственно равен 1 или 0. Хотя принципиально количество входов мажоритарного элемента может быть равно любому нечётному числу, на практике чаще всего применяются элементы с количеством входов 3 и 5.
Работа мажоритарного элемента на три входа описывается булевой функцией M(X,Y,Z) , определяемой следующей таблицей истинности (таблица 2).
Таблица 2 - Таблица
истинности
| X | Y | Z | M(X,Y,Z) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
СДНФ
данной функции
мажоритарности
запишется M(X,Y,Z)=![]() YZ+X
YZ+X![]() Z+XY
Z+XY![]() .
.
Минимизируя это выражение при помощи карт Карно, получим M(X,Y,Z)=XY+XZ+YZ.
Для этой функции вводится специальное обозначение, которое сокращает запись функции M(X,Y,Z)=XY+XZ+YZ=X#Y#Z.
Такая запись означает, что для получения из неё первоначальной минимальной ДНФ надо взять по коньюкции второго ранга по каждой переменной и объединить их знаком дизъюнкции. На рисунке 3 показана схема мажоритарного элемента на три входа и его условное обозначение.
X
& 1
![]() 2
2
Y & M
Z &
а) Мажоритарный элемент б) Условное обозначение
Рисунок 3 - Схема мажоритарного элемента и его условное обозначение
Похожие работы
... , выражать свою позицию, рефлексировать собственное поведение, самостоятельно принимать решения и т.п.» [20, с.351]. Именно такие ситуации возможно создавать при проведении лабораторного практикума. Студент, выполняя самостоятельно творческое задание исследовательского характера, проходит от начала до конца путь исследователя, решающего реальную научную проблему. Пройдя такой путь несколько раз ...
... работы со справочной системой работа практикума приостанавливается. 3. Организационно-экономическое обоснование проекта В ходе дипломного проекта был разработан компьютерный лабораторный практикум по курсу «Теория оптимизации и численные методы». В данном разделе рассмотрена экономическая сторона проекта. Рассмотрены следующие вопросы: 1) сетевая модель 2) расчёт ...
... был посвящен стендовый доклад на конференции ФССО-2001 [1]. Мы полагаем, что минимально необходимое число вариантов заданий разной степени трудности к одной лабораторной работе - три. Такое число обуславливается тем, что студентов, приступающих к выполнению лабораторного практикума, мы условно разделили по степени развития экспериментаторских навыков на три группы: большая группа студентов, для ...
... (ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ) НОВОТРОИЦКИЙ ФИЛИАЛ кафедра экономики и информатики КУРСОВАЯ РАБОТА РАЗРАБОТКА ЛАБОРАТОРНОГО ПРАКТИКУМА Исполнитель: Студент группы Руководитель: Дата допуска к защите: «__»_______200__г. Новотроицк 2001 1. СОЗДАНИЕ ТЕСТИРУЮЩИХ ПРОГРАММ С ИСПОЛЬЗОВАНИЕМ ВИЗУАЛЬНЫХ КОМПОНЕНТОВ1.1. Аналитический обзор В качестве ...
0 комментариев