Навигация
5. Выводы.
В результате моделирования работы СМО, а также анализ полученных данных и были сделаны следующие выводы:
1. При времени функционирования системы меньше 2000, работа системы нестабильна, трудно выявить какие-либо закономерности в поведении системы. Поэтому, чтобы сделать выводы об эффективности работы СМО, следует рассматривать её функционирование на временном интервале более 2000 единиц.
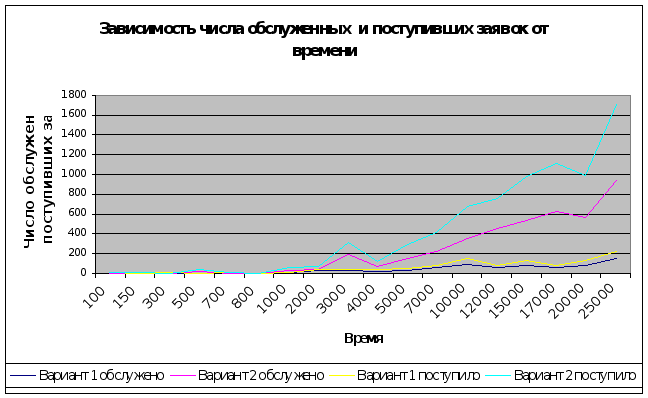
2. При увеличении времени функционирования системы соответственно увеличивается и количество заявок, поступивших в систему. Количество поступивших и обслуженных заявок увеличивается пропорционально увеличению времени работы системы. Причем, чем больше значения интенсивностей, тем больше быстрее увеличивается количество поступающих заявок с увеличением времени.
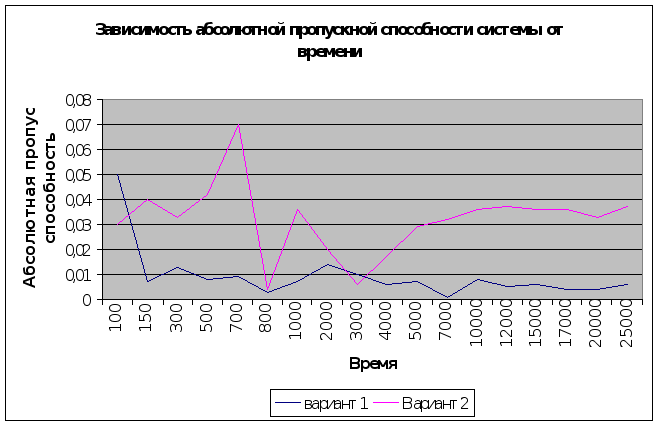
3. На интервале времени до 3000 значение абсолютной пропускной способности системы хаотически колебалось (особенно это заметно при втором варианте реализации). При времени больше 3000 амплитуда колебаний снизилась, а при времени Т7000 значения абсолютной пропускной способности системы для обоих вариантов приобретают стационарный характер, и примерно равны 0,004 для первого варианта работы системы и 0,036- для второго.
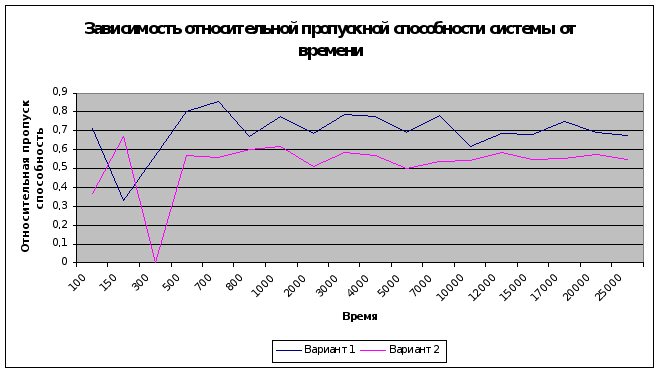
4. Значение относительной пропускной способности системы хаотически колебалось при всех временах функционирования. Однако, при больших временах амплитуда колебаний значительно снизилась. С увеличением времени заметна тенденция к стационарности в поведении величины относительной пропускной способности.
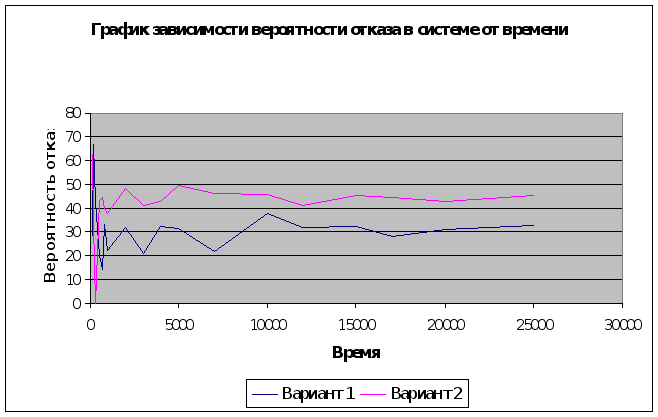
5. Т. к. вероятность отказа системы величена обратная относительной пропускной способности системы, то их поведение аналогично. При малых значениях времени (до 7000) вероятность отказа хаотично колебалась. А при увеличении времени, амплитуда колебания значительно снизилась. Практически вероятность отказа принимает стационарный характер при значении времени больше 17000.
Заключение.
Целью данного курсового проекта было построение модели двухканальной СМО с отказами и абсолютным приритетом. Модель СМО была и реализована с помощью программы в среде TURBO PASKAL. В процессе нескольких реализаций работы СМО для двух вариантов значений интенсивностей поступления заявок в были получены результаты функционирования системы. На основе полученных данных были построены графики, позволяющие провести исследование работы СМО. С помощью графиков проведен анализ полученных данных и сделаны выводы о работе систстемы.
Проведенное исследование наиболее наглядно отображают графики, приведенные в приложениях 2-4.
Приложение 1.
Результаты работы СМО.
| Характеристики работы СМО | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 |
| Время работы СМО | 100 | 100 | 150 | 150 | 300 | 300 | 500 | 500 | 700 | 700 | 800 | 800 | 1000 | 1000 | 2000 | 2000 |
| Поступило заявок | 7 | 8 | 3 | 9 | 7 | 3 | 5 | 37 | 7 | 9 | 3 | 5 | 9 | 58 | 41 | 78 |
| Обслужено заявок | 5 | 3 | 1 | 6 | 4 | 3 | 4 | 21 | 6 | 5 | 2 | 3 | 7 | 36 | 28 | 40 |
| Не обслужено заявок | 2 | 5 | 2 | 3 | 3 | 0 | 1 | 16 | 1 | 4 | 1 | 2 | 2 | 22 | 13 | 38 |
| Абсолютная пропускная способность системы | 0,05 | 0,03 | 0,007 | 0,04 | 0,013 | 0,1 | 0,008 | 0,042 | 0,009 | 0,07 | 0,003 | 0,004 | 0,007 | 0,036 | 0,014 | 0,02 |
| Относительная пропускная способность системы | 0,714 | 0,37 | 0,33 | 0,667 | 0,571 | 0 | 0,8 | 0,568 | 0,857 | 0,556 | 0,667 | 0,6 | 0,778 | 0,62 | 0,683 | 0,513 |
| Вероятность отказа, % | 28,6 | 62,5 | 66,7 | 33,3 | 42,9 | 0 | 20 | 43,2 | 14,3 | 44,4 | 33,3 | 40 | 22,2 | 37,9 | 31,7 | 48,7 |
| Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 | Вар 1 | Вар 2 |
| 3000 | 3000 | 4000 | 4000 | 5000 | 5000 | 7000 | 7000 | 10000 | 10000 | 12000 | 12000 | 15000 | 15000 | 17000 | 17000 | 20000 | 20000 | 25000 | 25000 |
| 38 | 318 | 37 | 121 | 48 | 291 | 87 | 413 | 147 | 672 | 88 | 762 | 124 | 975 | 88 | 1120 | 129 | 989 | 218 | 1707 |
| 30 | 187 | 25 | 69 | 33 | 147 | 68 | 222 | 91 | 363 | 60 | 448 | 84 | 533 | 66 | 618 | 89 | 566 | 147 | 932 |
| 8 | 131 | 12 | 52 | 15 | 144 | 19 | 191 | 56 | 309 | 28 | 314 | 40 | 442 | 22 | 502 | 40 | 423 | 71 | 775 |
| 0,01 | 0,006 | 0,006 | 0,017 | 0,007 | 0,029 | 0,001 | 0,032 | 0,008 | 0,036 | 0,005 | 0,037 | 0,006 | 0,036 | 0,004 | 0,036 | 0,004 | 0,033 | 0,006 | 0,037 |
| 0,789 | 0,588 | 0,776 | 0,57 | 0,688 | 0,505 | 0,782 | 0,538 | 0,619 | 0,54 | 0,682 | 0,588 | 0,677 | 0,547 | 0,75 | 0,552 | 0,69 | 0,572 | 0,674 | 0,546 |
| 21,1 | 41,2 | 32,4 | 43 | 31,3 | 49,5 | 21,8 | 46,2 | 38,1 | 46 | 31,8 | 41,2 | 32,3 | 45,3 | 28 | 44,8 | 31 | 42,8 | 32,6 | 45,4 |
Приложение 2.
Приложение 3.
Приложение 4.
Приложение 5.
Приложение 6.
Листинг программы.
PROGRAM CAN_SMO;
TYPE
CHANNAL = (FREE, CLAIM1, CLAIM2);
TIME = word;
INTENSITY = word;
STATISTICS = word;
VAR
CHANNAL1, CHANNAL2 : CHANNAL;{Каналы }
_T_, t, tc1, tc2 : TIME; {Время}
l1, l2, n1, n2 : INTENSITY; {Интенсивности }
served1, not_served1,
served2, not_served2,
S : STATISTICS; {Статистика}
M,N:INTEGER;{число реализаций}
FUNCTION W(t : TIME; l : INTENSITY) : boolean;{Определяет появилась ли заявка}
Begin {по интенсивности потока l}
if random < l/60 then W := TRUE else W := FALSE;
End;
FUNCTION F(t : TIME; n : INTENSITY) : TIME;{Определяет сколько будет обрабатываться заявка}
Begin {по интенсивности обслуживания заявок n}
F := t +round(60/(n));
End;
BEGIN
M:=0;
WRITELN('ВВЕДИТЕ ЧИСЛО РЕАЛИЗАЦИЙ РАБОТЫ СМО');
READLN(N);
REPEAT
M:=M+1;
writeln(M, '-ая реализация');
randomize;
CHANNAL1 := FREE; CHANNAL2 := FREE;
l1 := 3; l2 := 1; n1 := 2; n2 := 1;
served1 := 0; not_served1 := 0;
served2 := 0; not_served2 := 0;
write('Введите время исследования СМО - Т: '); readln(_T_);
repeat
if tc1 = t then
begin
if CHANNAL1 = CLAIM1 then inc(served1) else inc(served2);
CHANNAL1 := FREE;
writeln('Канал1 выполнил заявку');
end;
if tc2 = t then
begin
if CHANNAL2 = CLAIM1 then inc(served1) else inc(served2);
CHANNAL2 := FREE;
writeln('Канал2 выполнил заявку');
end;
if W(t,l1) then
begin
writeln('Поступила заявка1');
if CHANNAL1 = FREE then
begin CHANNAL1 := CLAIM1; tc1 := F(t,n1); writeln('Канал1 принял заявку1'); end
else if CHANNAL2 = FREE then
begin CHANNAL2 := CLAIM1; tc2 := F(t,n1); writeln('Канал2 принял заявку1'); end
else if CHANNAL1 = CLAIM2 then
begin CHANNAL1 := CLAIM1; tc1 := F(t,n1); inc(not_served2); writeln('Канал1 принял заявку1 вместо заявки2'); end
else if CHANNAL2 = CLAIM2 then
begin CHANNAL2 := CLAIM1; tc2 := F(t,n1); inc(not_served2); writeln('Канал2 принял заявку1 вместо заявки2'); end
else begin inc(not_served1); writeln('заявка1 не обслужена'); end;
end;
if W(t,l2) then
begin
writeln('Поступила заявка2');
if CHANNAL1 = FREE then
begin CHANNAL1 := CLAIM2; tc1 := F(t,n2); writeln('Канал1 принял заявку2');end
else if CHANNAL2 = FREE then
begin CHANNAL2 := CLAIM2; tc2 := F(t,n2); writeln('Канал2 принял заявку2');end
else begin inc(not_served2); writeln('заявка2 не обслужена'); end;
end;
inc(t);
until _T_ = t;
S := served1 + not_served1 + served2 + not_served2;
writeln('время работы СМО ',_T_);
writeln('обслужено каналом1: ' ,served1);
writeln('обслужено каналом2: ',served2);
writeln('Поступило заявок : ',S);
writeln('Обслужено заявок : ',served1+served2);
writeln('Не обслужено заявок : ',not_served1+not_served2);
{writeln('Интенсивность поступления заявок в систему : ',(served1+served2)/_T_:2:3);}
writeln('Абсолютная пропускная способность системы : ',(served1+served2)/T:2:3);
writeln('Вероятность отказа : ',(not_served1+not_served2)/S*100:2:1,'%');
writeln('Относительная пропускная способность системы: ',(served1+served2)/S:2:3);
readln;
UNTIL M>=N;
writeln('моделирование закончено');
END.
Список литературы.
Фомин Г.П., Математические методы и модели в коммерческой деятельности. М: Финансы и статистика, 2001.
Вентцель Е.С., Овчаров Л.А. Теория вероятностей и её инженерные приложения, М: Наука, 1988.
Вентцель Е.С. Исследование операций, М:Наука, 1980.
Лифшиц А.Л. Статистическое моделирование СМО, М., 1978.
Советов Б.А., Яковлев С.А. Моделирование систем, М: Высшая школа, 1985.
Гмурман В.Е. Теория вероятностей и математическая статистика, М: Высшая школа, 2001.
Похожие работы
... техники на 2000 рублей в день. Это позволит получить прибыль 1779337 рублей в месяц. ЗАКЛЮЧЕНИЕ В данном курсовом проекте представлена тема "Математическое моделирование и оптимизация системы массового обслуживания". Системы массового обслуживания имеют огромное практическое применение в наше время, что показано в рассмотренном примере. Целью данного курсового проекта было определение - ...
... сколько их уже исправно и ждет наладки. Классификация СМО далеко не ограничивается приведенными разновидностями, но этого достаточно.2. Системы массового обслуживания с ожиданием 2.1 Одноканальная СМО с ожиданием Рассмотрим простейшую СМО с ожиданием — одноканальную систему (n - 1), в которую поступает поток заявок с интенсивностью ; интенсивность обслуживания (т.е. в среднем непрерывно ...
... как точки на временной оси. Для достижения основной цели моделирования достаточно наблюдать систему в моменты реализации основных событий. Рассмотрим пример одноканальной системы массового обслуживания. Целью имитационного моделирования подобной системы является определение оценок ее основных характеристик, таких, как среднее время пребывания заявки в очереди, средняя длина очереди и доля ...
... 2-3 Поиск литературы 7 1 7 2-4 Разработка модели разветвленной СМО 6 1 6 3 Поиск литературы завершен 3-6 Изучение литературы по теории массового обслуживания 10 1 10 4 Модель разработана 4-5 Разработка алгоритма программы 10 1 10 5 Алгоритм программы разработан 5-7 Выбор среды программиро-вания и создание программы 30 1 ...


0 комментариев