Навигация
3.3 Принцип сбора данных.
Данные были собраны путем просмотра “прайс-листов” за период с 14.10.97 по 15.12.97 , которые фирма хранила как в базе данных компьютера, в глобальной сети Internet, а так же и в “подшитом” виде.
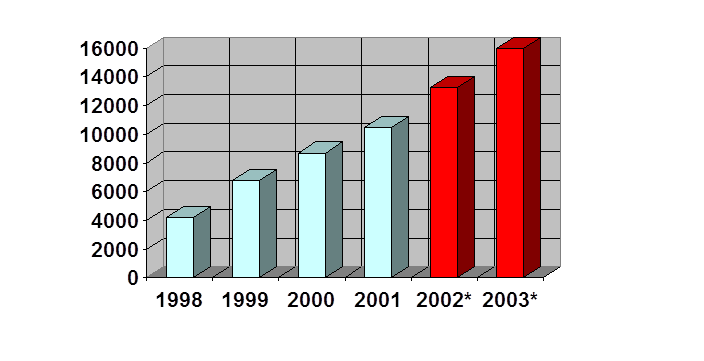
График исходных данных.
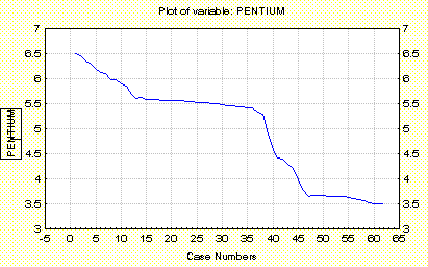
ГЛАВА 4. Компонентный анализ.
Оценка Тренда.
Тренд - это некоторая функция времени. Тренд характеризует основную закономерность движения во времени, свободную в основном (но не полностью) от случайных воздействий.
Обычно полученная траектория связывается исключительно со временем. Предполагается, что рассматривая любое явление как функцию времени, можно выразить влияние всех остальных факторов. Механизм их влияния в явном виде не учитывается. Исходя из вышесказанного под трендом понимается регрессия на время. Более общее понятие тренда весьма удобное на практике, - это детерминированная составляющая динамики развития, определяемая влиянием постоянно действующих факторов. Отклонения от тренда являются случайной составляющей.
Оценка тренда возможна на основе двух подходов:
оценка на основе гладких функций х = f(x); (параметрические методы)
на основе разного рода скользящих средних (непараметрические методы)
Я оценивала тренд методом вторых разностей.
X - 0.000-1.00*X(t-1); X-0.000-1.00*x(t-1)
Удаление Тренда
Иногда из некоторых временных рядов нужно удалить линейный ил медленно меняющийся тренд . Такого рода тренды наблюдаются в рядах, например, при суммировании одной или нескольких компонент, приводящим к ошибкам двух типов. Во-первых при неправильной калибровке нулевой точки каждый момент отбора данных будет возникать небольшая ошибка. После суммирования эта постоянная величина даст прямую. Такой линейный тренд может привести к большим ошибкам при определении плотности спектра мощности и в связанных с этим вычислениях . Ошибка второго типа возникает из-за возрастания в процессе суммирования мощности, соответствующей низкочастотному шуму. Как правило такой шум в данных всегда есть. При суммировании он обретает форму случайного, но медленно меняющегося тренда. Насколько быстро меняется такой тренд, до некоторой степени зависит от интервала квантования.
Наилучшим способом удаления тренда служит применение высокочастотных фильтров. Полимиальный тренд можно удалять методом наименьших квадратов. Если требуется удаление многочленов только низких порядков, то решение соответствующей системы методом обратной матрицы можно свести к непосредственному вычислению коэффициентов с использованием памяти ЭВМ.
После того как удалили тренд, то получили стационарный ряд.
На графике можно увидеть остатки после удаления тренда.
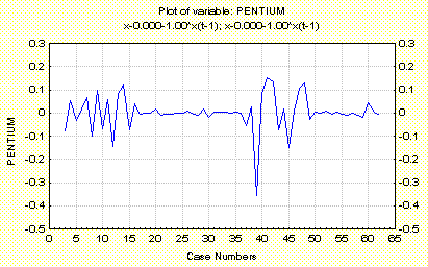
Стационарный ряд выглядит как не совсем регулярные колебания, около некоторого среднего уровня.
Стационарный случайный процесс может быть представлен в виде суммы гармонических колебаний различных частот, называемых гармониками.
Функция, описывающая распределение амплитуд этого процесса по различным частотам, называется спектральной плотностью. График называется спектром.
Спектр (периодическая шкала).
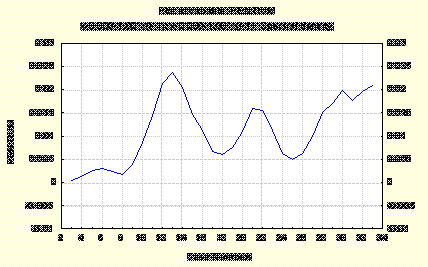
Спектр показывает, какого рода колебания преобладают в данном процессе, какова его внутренняя структура.
Стационарная случайная функция Х(t) может быть представлена ввиде канонического разложения:
Ґ
X(t) = е (UkCOSWkT + VkSINWkT)
k=0
где Uk,Vk - некоррелированные случайные величины с математическими ожиданиями, равными нулю, и одинаковыми дисперсиями, т.е.
D(Uk) = D(Vk ) = Dk.
Такое разложение называется спектральным разложением стационарного случайного процесса X = Х(t). Спектр стационарной случайной функции описывает распределение дисперсий по различным частотам.
Дисперсия стационарной случайной функции равна сумме дисперсий всех гармоник ее спектрального разложения.
Отсюда делаем вывод, что дисперсия величины Х(t) определенным образом распределена по различным частотам: одним частотам соответствует большая дисперсия, другим - меньшая дисперсия.
Функция x(w) = Dk/W называется спектральной плотностью дисперсии или спектральной плотностью стационарной случайной функци Х(t).
При анализе временных рядов применяется спектральный анализ стационарных случайных функций.
Целью спектрального анализа временных рядов является оценка спектра ряда. Спектром временного ряда, является разложение дисперсии ряда по частотам для определения существенных гармонических составляющих.
Значение спектра оценивается по формуле:
m
f (Wj ) = 1/2p {hoco+2 е hk ck cos Wj k}
k=1
где Wj - частоты, для которых оцениваются спектры:
Wj =p j/ ; j = 1,2,...m;
где ck - автоковариационная функция;
hk - специально подобранные веса значений ковариационной функции,
зависящие от частоты m;
hk - еще называют кореляционным окном;
m - целое число называемое точкой усечения или числом
используемых сдвигов и представляющее собой число частотных
полос, для которых оценивается спектр.
Чем больше m , тем больше точек оцениваемого спектра, а следовательно, и больше дисперсия оценки в каждой точке.
Чем меньше m, тем лучше оценка.
Величина m зависит от длины временного ряда.
На графике где изображен спектр можно проследить возрастание и убывание спектра, на графике также можно наблюдать пики т.е. отклонения от тренда.
Но также исходя из этого, можно увидеть что временной ряд не имеет периодичности, т. е. нет исходных повторяющихся особенностей ряда.
Кроме того, спектральный анализ можно еще рассмотреть путем изучения сезонных колебаний. Это бы позволило выявить периодические составляющие исследуемого ряда с целью повышения точности прогнозирования.
В данной работе удаление сезонной компоненты не представляет возможности, так как исследуемый ряд не имеет сезонности.
11
Башкирский Государственный Университет
Кафедра финансов и налогообложения
ПРИЛОЖЕНИЕ к курсовой работе на тему: Прогнозирование цены на комьютер Pentium 166 на 19 декабря 1997 года.
Выполнила: студентка дн.от.
эк.ф-та,3-го курса,гр. 3.4ЭЮ
Хакимова Д.И.
Проверила: научный рук-ль,
доцент ,к.э.н.
Саяпова А.Р.
г. Уфа 1997 г.
Содержание приложения:
Удаление тренда различными способами используемые программой Statistika версии 4.3
Модель Holt (a =0.300,a=0.800)
Модель Winters (a =0.300,a=0.800)
Модель Брауна (a =0.300,a=0.800)
Регрессионная модельУдаление тренда различными способами используемые программой Statistika версии 4.3
Я работала в программе Statistica 4.3 которая позволяет удалить тренд, исходя из ниже предложенных графиков можно увидеть различные способы для его удаления. Но эти способы не явились более подходящими, и поэтому представлены для анализа проделанной курсовой работе.
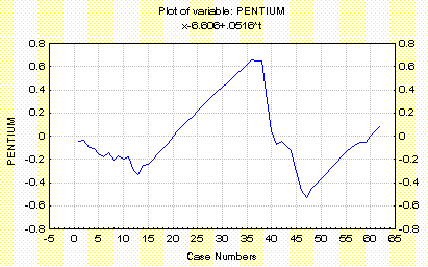
На этом графике использовался метод Trend subtract
(x=x-(a+b*t)), где а= 6.606, b = -0.52 .
Тренд в данном случае неудалился, так как сам тренд не линейный.
Сделав вывод, что тренд не линейный, я проделала попытку удалить тренд в Nonlinear Estimatoin получила следущее:
| Model: PENTIUM = b1+b2/t+b3/t**2 | |||
N=62 | Dep.var: PENTIUM loss (OBS - PRED)**2 FINAL loss:31.852464424 R=.67433 variance explained: 45.473% | ||
| b1 | b2 | b3 | |
| Estimate | 4.34597 | 11.85681 | -10.0804 |
График удаления тренда не линейным способом:
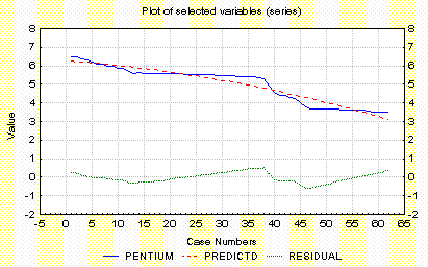
Выше описанным способом тренд тоже не удалился.
Модель Holt (a =0.300,a=0.800)
Примером адаптивной модели предназначенной для прогнозирования сезонных процессов, является модель Хольта. Эта модель предполагает мультипликативное объединение линейного тренда и сезонные составляющие во временном ряду.
Модель Хольта при a = 0.300
Exp.smoothing: SO=6.534 TO = 0.49
| TIME SERIES Summury of error | Lin.trend; no season; Alpha= 0.300 Gamma=0.1 PENTIUM Error |
| Mean error | .00731672825436 |
| Mean absolute error | .13134104302219 |
| Sums of squares | 1.96424677027454 |
| Mean squares | .03168139952056 |
| Mean percentage error | .26328877539247 |
| Mean abs. pers. | 3.01698849598955 |
График по Хольту с a = 0.300
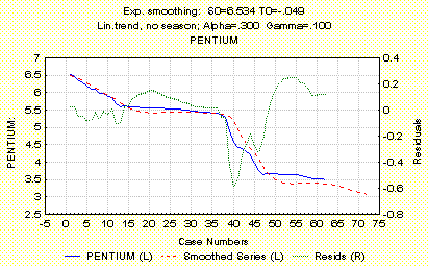
Exp.smoothing: SO=6.534 TO = 0.49
| CASE | SMOOTHED SERIES |
| 16.12.97 | 3.379367 |
| 17.12.97 | 3.343613 |
| 18.12.97 | 3.307860 |
| 19.12.97 | 3.272107 |
Модель Хольта при a = 0.800
Exp.smoothing: SO=6.534 TO = 0.49
| TIME SERIES Summury of error | Lin.trend; no season; Alpha= 0.800 Gamma=0.1 PENTIUM Error |
| Mean error | .00315177373958 |
| Mean absolute error | .05706002635321 |
| Sums of squares | .48259413419920 |
| Mean squares | .00778377635805 |
| Mean percentage error | .12944834490985 |
| Mean abs. pers. | 1.26337346085392 |
График по Хольту с a = 0.800
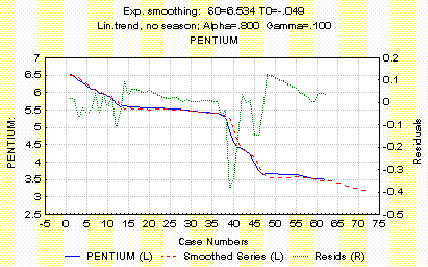
Exp.smoothing: SO=6.534 TO = 0.49
| CASE | SMOOTHED SERIES |
| 16.12.97 | 3.457111 |
| 17.12.97 | 3.423383 |
| 18.12.97 | 3.398655 |
| 19.12.97 | 3.355927 |
Модель Winters (a =0.300,a=0.800)
Модель Уйнтерса при a = 0.300
Exp.smoothing:Multipl.season(12) SO=6.433 TO = 0.52
| TIME SERIES Summury of error | Lin.trend; no season; Alpha= 0.300 Delta=.100; Gamma=0.1 PENTIUM Error |
| Mean error | .00850967552279 |
| Mean absolute error | .13196744584935 |
| Sums of squares | 2.02519074270767 |
| Mean squares | .03266436817876 |
| Mean percentage error | .27239869561423 |
| Mean abs. pers. | 3.02001823889308 |
График по Уинтерсу с a = 0.300
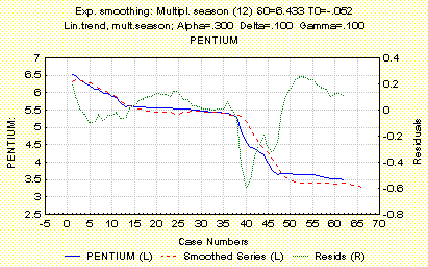
Exp.smoothing:Multipl.season(12) SO=6.433 TO = 0.52
| CASE | SMOOTHED SERIES |
| 16.12.97 | 3.373012 |
| 17.12.97 | 3.337162 |
| 18.12.97 | 3.309019 |
| 19.12.97 | 3.283079 |
Модель Уйнтерса при a = 0.800
Exp.smoothing:Multipl.season(12) SO=6.433 TO = 0.52
| TIME SERIES Summury of error | Lin.trend; no season; Alpha= 0.800 Delta=.100; Gamma=0.1 PENTIUM Error |
| Mean error | .00387269483310 |
| Mean absolute error | .06040575200437 |
| Sums of squares | .54276104822497 |
| Mean squares | .00875421046649 |
| Mean percentage error | .14058659957529 |
| Mean abs. pers. | 1.32624409579650 |
График по Уинтерсу с a = 0.800

Exp.smoothing:Multipl.season(12) SO=6.433 TO = 0.52
| CASE | SMOOTHED SERIES |
| 16.12.97 | 3.453841 |
| 17.12.97 | 3.429777 |
| 18.12.97 | 3.407928 |
| 19.12.97 | 3.380729 |
Модель Брауна (a =0.300,a=0.800)
Модель Брауна может отображать развитие не только в виде линейной тенденции, нои в виде случайного процесса, не имеющего тенденции, а также ввиде изиеняющейся параболической тенденции.
Модель Брауна при a = 0.300
Exp.smoothing: SO=4.982
| TIME SERIES Summury of error | Lin.trend; no season; Alpha= 0.300 PENTIUM Error |
| Mean error | -.0780414476807 |
| Mean absolute error | .1978141110028 |
| Sums of squares | 6.8610393089365 |
| Mean squares | .1106619243377 |
| Mean percentage error | -2.2104491142263 |
| Mean abs. pers. | 4.0726990990745 |
График по Брауну с a = 0.300

Exp.smoothing: SO=4.982
| CASE | SMOOTHED SERIES |
| 16.12.97 | 3.530736 |
| 17.12.97 | 3.530736 |
| 18.12.97 | 3.530736 |
| 19.12.97 | 3.530736 |
Модель Брауна при a = 0.800
Exp.smoothing: SO=4.982
| TIME SERIES Summury of error | Lin.trend; no season; Alpha= 0.300 PENTIUM Error |
| Mean error | -.0298811251614 |
| Mean absolute error | .08804695430620 |
| Sums of squares | 3.1058602054085 |
| Mean squares | .05009465809765 |
| Mean percentage error | -.90807550618029 |
| Mean abs. pers. | 1.70449937474829 |
График по Брауну с a = 0.800
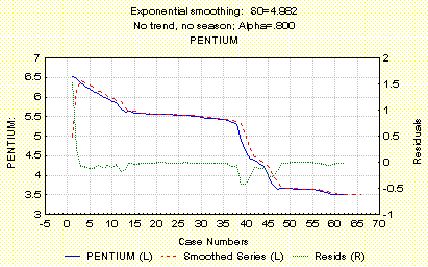
Exp.smoothing: SO=4.982
| CASE | SMOOTHED SERIES |
| 16.12.97 | 3.500203 |
| 17.12.97 | 3.500203 |
| 18.12.97 | 3.500203 |
| 19.12.97 | 3.500203 |
Прогнозирование по вышеуказанным моделям получается не совсем стабильным.
Регрессионная модель
В экономической деятельности очень часто требуется не только получать прогнозные оценки исследуемого показателя, но и количественно охарактеризовать степень влияния на него других факторов.
Рассматривая зависимость цены на компьютер Pentium166 и инфляции я получаю:
REGRESSION SUMMARY for Dependent Variable: PENTIUM
| R=.68998993 RI=.47608611 Abjusted RI=.45593557 F(1,26)=23.626 p | ||||||
Похожие работы
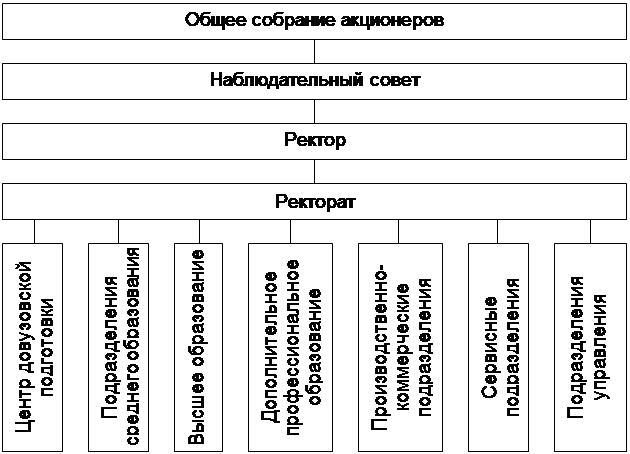
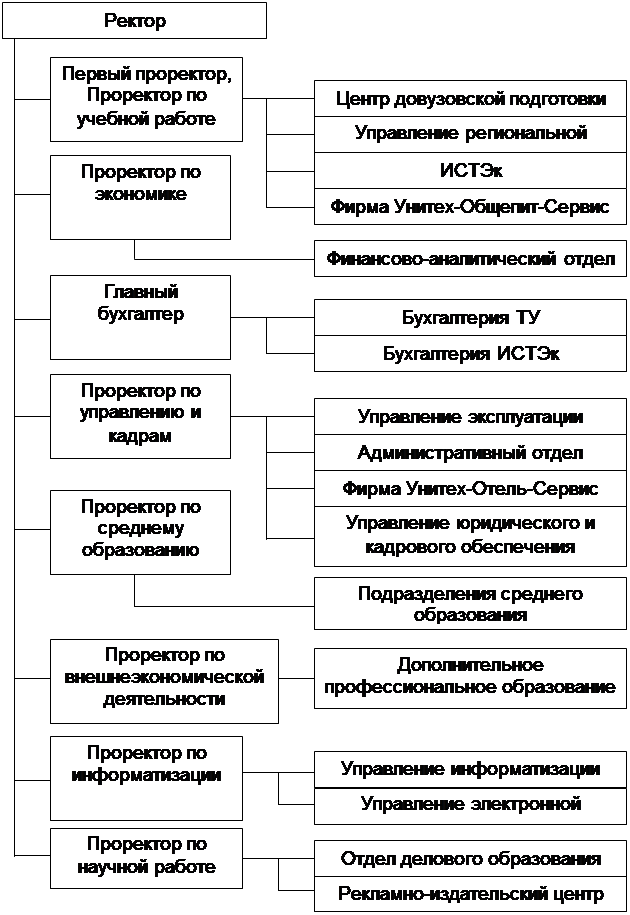
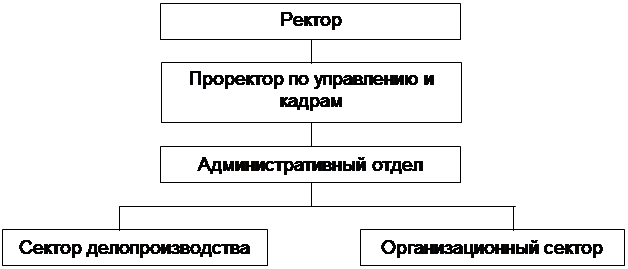
... , несмотря на такое лидерство, еще рано говорить о том, что информационные системы прочно вошли жизнь современных управленцев. 2 АНАЛИЗ ИНФОРМАЦИОННОГО ОБЕСПЕЧЕНИЯ УПРАВЛЕНИЯ ПРЕДПРИЯТИЕМ 2.1 Общая характеристика объекта исследования ОАО «Технический университет КубГТУ» был создан 9 октября 1992 года. Новые экономические условия требовали создания в Кубанском государственном ...
... период подготовки планов. Еще одна категория систем, используемых для бюджетирования - корпоративные системы управления (ERP-системы). ERP (Enterprise Resource Planning) - автоматизация и оптимизация внутренних бизнес-процессов, планирование как материальных, так и финансовых ресурсов в масштабе предприятия; - используется для описания компонентов "производство", "логистика", "финансы". ERP- ...
... владельцев компьютеров увеличилась более чем в 2 раза, что говорит о больших перспективах для развития нашего бизнеса. Потенциал павлодарского рынка можно оценить в 50-60 тысяч человек. Статистические данные были собраны путем опроса продавцов компьютерных компаний, а также благодаря информации предоставленной Областным управлением по статистике и анализу информации. 2.2 ИССЛЕДОВАНИЯ РЫНКА Г. ...
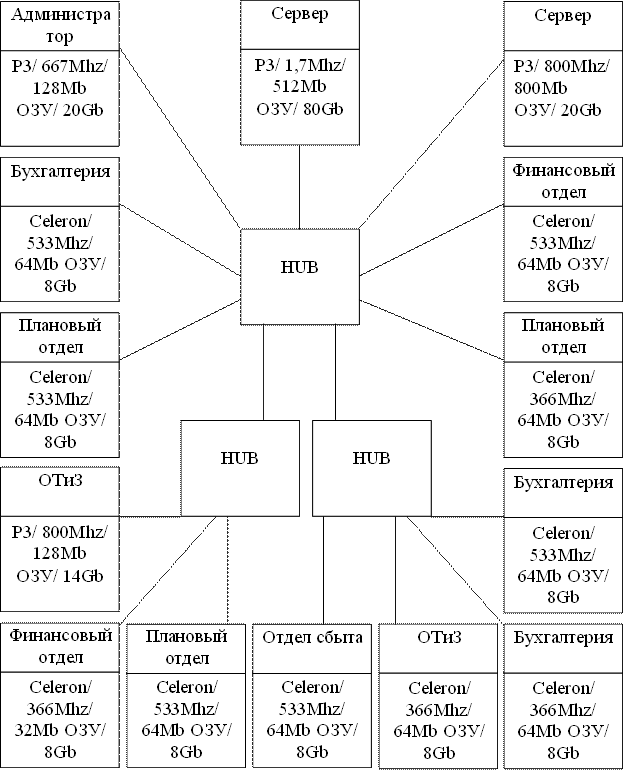
... ; - отдельная пиктограмма для форматирования; - появление механизма Drag & Plot, предназначенного для быстрой активизации диаграмм. 4.6. Техническое обеспечение. Автоматизированная система бухгалтерского учета Министерства здравоохранения Республики Тыва может функционировать при следующей конфигурации аппаратных средств: IBM совместимый компьютер с процессором 80386 фирмы Intel, ...
0 комментариев