Долговременный экономический рост

8.5. Долговременный экономический рост

В длинное время цикличность экономического роста перестает быть заметной, основное значение приобретают средние темпы эко­номического роста. При долговременном экономическом росте даже небольшие различия в темпах прироста выпуска со временем накап­ливаются и ведут к существенному росту ВНП на душу населения и тем самым к высокому уровню жизни. При росте ВНП на душу насе­ления на 2% в год его удвоение происходит каждые 35 лет.

В 50-80-е гг. наиболее впечатляющие темпы экономического рос­та наблюдались в Японии(в %):

1955-1973 1973	1979	1980	1981	1982-1983	1984	1985	1986	1987	1988	1900
10	5,2	4,8	4.0	3,15	5,1	4,6	3,25	3	4,9	4.0

Это позволило Японии занять первое место по ВНП на душу на­селения,

Большая часть длинного времени относится к прошлому време­ни, в котором исчезает неопределенность, присущая будущему вре­мени. Поэтому основную роль в долговременном росте играют реальные факторы, а номинальные величины выполняют вспомогатель­ные функции.

Для теоретического моделирования долговременного экономи­ческого роста используют понятие производственной функции. Оно определяет максимальную величину выпуска продукции, которая мо­жет быть получена при использовании данных значений капитала, труда, земли и сырья и данном технологическо-организационном уровне:

Y=AF(K,L), (1)

 где А — инновационные изменения. Соответственно прираще­ние дохода рассматривается в виде:

Y =Δмрк*Δк + mplxΔl + ΔAF (2)

где первое слагаемое есть увеличение производства в результате роста объема капитала, второе — увеличение производства в резуль­тате роста затрат труда, третье — действие инновационного потока (напомним, что МРК — предельная производительность капитала, MPL — предельная производительность труда). Преобразуем (2) следующим образом:

(МРК*К)ΔК/К + (MPL*L)ΔL/L + ΔА/А(А*F), откуда

Y/Y = ((мрк*к)/Y)*(Δк/к) + ((MPL*L)/Y) * (ΔL/L)*ΔA/A(A*F)/Y (3)

При совершенной конкуренции и постоянной отдаче от масшта­ба доход факторов равен их предельному продукту, а вознагражде­ние факторов. Поэтому (MPK*K)/Y = Pr/Y = (доля капитала в ВНП) и (MPL*L)/Y= W/Y = 1- (доля труда в ВНП). С использованием этих равенств из (1) и (3) получаем

ΔY/Y = a(ΔК/К) + (l-a)(ΔL/L) + ΔА/А (4)

Это уравнение выведено в предположении постоянной отдачи от масштабов производства. Если ΔК/К = 1 % и ΔL/L = 1 %, то и ΔY/Y = 1 %. При возрастающей отдаче от масштаба в этом случае ΔY/Y > 1 %. Из (4) сразу следует равенство ΔА/А= ΔY/Y - а(ΔК/К) - (1-a)(ΔL/L) (5) Из него видно, что ΔА/А есть та часть темпа прироста выпус­ка, которая не может быть объяснена изменением затрат факторов (остаток Солоу) и которая, следовательно, представляет собой до­лю совокупного выпуска, произведенную за счет технологических и иных изменений (инноваций различного рода). Строго говоря, ос­таток Солоу — это просто часть экономического роста, которая обусловлена факторами, не поддающимися прямым измерениям. Вопрос о правильной интерпретации этого остатка все еще остает­ся проблемой.

Тем не менее в первом приближении остаток Солоу определяет­ся техническим прогрессом (ростом совокупной производительности факторов). Выпуск растет за счет улучшения методов производства при неизменных затратах труда и капитала (с помощью тех же количеств факторов можно получить больше продукции). Значительную часть это­го остатка дает улучшение знаний и улучшение размещения ресурсов.

Зная величины, входящие в (5) справа, можно вычислить и до­лю технологического прогресса в экономическом росте. Пусть, на­пример, ΔY/Y =3,1%, ΔК/К = 2,5%, ΔL/L = 1,5%, а = 1/4. Тогда ΔА/А = 3,1% - 2,5%*0,25 - 1,5%*0,75 = 1,35%.

Для развитых стран именно технологическая составляющая об­разует основу экономического роста. Так, за 1909-1949 гг. выпуск в США на одного работающего удвоился. При этом только 12% этого роста были получены за счет увеличения капитала, остальные 88% пришлись на долю остатка Солоу. Сходная картина во всех развитых странах, но в развивающихся странах картина обратная. Резкое ослаб­ление темпов экономического роста после 1973 г. частично может быть объяснено ростом цен на нефть, увеличившим издержки и сократив­шим экспорт, а частично — уменьшением воздействия на рост остат­ка Солоу (ослаблением инновационных потоков).

Для того, чтобы показать важность технологического прогресса для рыночной экономики, т.е. справедливости неравенства ΔА/А > 0, допу­стим, напротив, что технологический прогресс отсутствует: ΔА/А = 0. Допустим также, что К > L. Тогда величины K/L и Q/L растут. Каждый рабочий приводит в действие больше капитала, его предельная произ­водительность растет, поэтому в конкурентной экономике растет и его реальная заработная плата, пропорциональная его предельной произво­дительности.

Графически имеем следующую картину (ΔА/А = 0, L = const.):

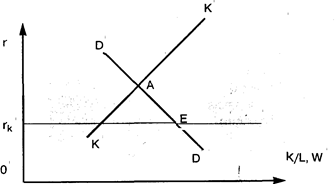
При сделанных предположениях кривая DD спроса на капитал наклонена вниз, так как для данного количества труда увеличение накопления капитала при неизменной технологии уменьшает его про­изводительность.

Действительно,

(6) Q/L = Q/K*K/L

С ростом К производительность труда Q/L растет, но меньшим темпом, чем капиталовооруженность труда K/L, поэтому производи­тельность капитала Q/K уменьшается. Падение предельной произво­дительности капитала уменьшает долгосрочное значение г.

КК — кривая предложения капитала. Она имеет положитель­ный наклон, поскольку предложение капитала растет с ростом г. Точка А пересечения DD и КК соответствует равновесию рынка ка­питалов.

Это равновесие, однако, неустойчиво в длинное время. Его не­устойчивость связана с существованием критической величины про­цента rk. Если r > rk, то чистые сбережения в экономике положитель­ны, при r = rk они равны нулю, а при г < rk отрицательны. Поэтому при любом r > rk предложение капитала увеличивается, но интен­сивность этого предложения падает с уменьшением r. На диаграмме этому соответствует сдвиг КК вправо. В результате состояние эко­номики скользит вниз по DD, приближаясь постепенно к Е. При этом W, K/L и Q/L растут, а r падает. В точке Е r = rk и уменьшение же­лания сберегать прекращает дальнейшее накопление капитала. W и r перестают изменяться. Это может произойти при высоком уровне дохода и выпуска, если было накоплено значительное количество ка­питала.

Допустим теперь, что ΔA/A > 0. Тогда можно увеличить Q при тех же К и L. Кривая DD сдвигается вправо и вверх, и r увеличивает­ся. При постоянном сдвиге DD вправо вместо движению к равнове­сию с постоянными Q, W и г экономика сдвигается в состояние, в котором K/L, Q/L и W растут со временем, а r не уменьшается. В про­тивном случае Маркс был бы прав, говоря о неизбежном падении нор­мы прибыли.

Наблюдения за последние 100 лет показывают, что для промышленно развитых стран:

1. Население и предложение труда растут, но более скромным темпом, чем запас капитала, и это ведет к росту капиталовооружен­ности K/L.

2. Имеется явная тенденция к повышению реальной заработной плати. Доля совокупной заработной платы в ВНП медленно растет на больших интервалах времени.

3. Вместо падения нормы прибыли на капитал (и тем самым уменьшения величины процента) наблюдаются значительные её коле­бания на протяжении делового цикла без какой-либо строгой тенден­ции к увеличению или понижению. Пои этом величина Q/K растет.

4. После сглаживания траекторий деловых циклов обнаружива­ется, что ВНП устойчиво растет с темпом 3-4% в год. Это значитель­но выше средневзвешенных затрат капитала, труда и ресурсов.

Это позволяет заключить, что модель Солоу приблизительно пра­вильно описывает долговременный экономический рост. При заданных значениях технологических изменений и прироста капитала вы­пуск растет в зависимости от уровня занятости, что соответствует классической модели.

Вместе с тем модель позволяет улавливать важные нюансы, анализ которых мы начнем с упрощающего предположения о посто­янстве отдачи от масштаба. В этом случае AF(K, L) = LΔF(K/L). Обо­значим через q выпуск на одного работающего и через k — количест­во капитала на единицу труда: q = Y/L, k = K/L. Тогда Y/L = AF(K/L) и (1) можно записать в виде:

q=AF(k) (2)

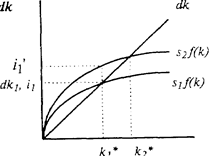
т.е. выпуск на душу населения является возрастающей функци­ей отношения «капитал — труд». Графически имеем:

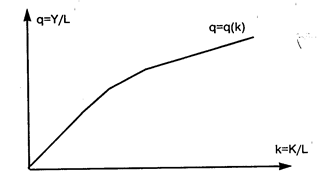
Как видим, график q растет с ростом k, но с убывающим тем­пом. Угол наклона этой функции равен предельной производитель­ности капитала, которая падает с ростом К.

Положим в основном уравнении (4) DA/A = 0 (инновационные потоки в экономике отсутствуют), ΔL/L = п (темп прироста рабочей силы постоянен и равен п). Тогда в (4) остается только одна перемен­ная — темп прироста капитала, зависящая от S и Y.

Назовем состояние экономики стационарным, если DA/A = 0 и Y/L = const (т.е. если производительность труда не изменяется). В этом случае Y/L = ΔY/ΔL, или ΔY/Y = ΔL/L. Но ΔL/L = п, поэто­му и ΔY/Y = n. Из (4) получаем, что в стационарном состоянии верно также ΔК/К = п. Таким образом, в стационарном состоянии темп прироста запаса капитала и темп экономического роста равны тем­пу роста населения.

Обратим теперь внимание на то, что величина ΔК есть просто ин­вестиции I, которые в закрытых моделях без государства равны сбе­режениям. Поэтому имеем:

1.    ΔK=I-dK (d - норма замещения капитала)

2.    S=sY (s=const)

3.    ΔK=sY-dK 1),2)

4.    ΔK/K=sY/K-d 3), деление на K

5.    n=sY/K-d 4), подстановка ΔK/K=n

6.    sY=(n+d)K 5)

Последнее равенство означает, что в стационарном состоянии сбе­режений хватает как раз для того, чтобы обеспечить достаточно инве­стиций для покрытия амортизации и оснащения новых работников стандартной величиной капитала. Если бы сбережения были больше этой величины, то капитал на душу населения увеличивался бы, ведя к росту выпуска на душу населения. Если бы сберегалось недостаточ­но, то капитал и доход на душу населения сокращались бы. В стацио­нарном состоянии, следовательно, нет ни избыточных сбережений, ни избыточных инвестиций.

Разделив обе стороны равенства 6) на L, получаем

7. sy = (n + d)k

С достижением равенств б) и 7) объем капитала на одного рабо­тающего и объем выпуска на одного работающего достигают своих равновесных значений и больше не меняются, если только экономи­ка не подвергается сильным экзогенным воздействиям. Значение k, удовлетворяющее равенству 7), обозначим через k*.

Допустим теперь, что экономика не находится в стационарном состоянии. В этом случае темп прироста капиталовооруженности ра­вен разности между темпами прироста капитала и труда:

8. Δk/k = ΔK/K-n

Далее рассуждаем следующим образом:

9. Δk/k = (sY-dK)/K-n 8), 3)

10. Δk/k = sY/K - d-n 9)

11. Δk/k = s(Y/L)/(K/L) - d-n

12. Δk/k = sy/k-d-n

13. Δk = sy + k(d+n)

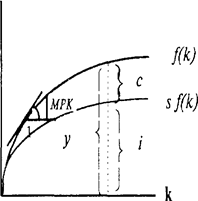
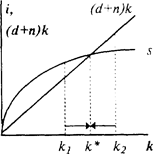
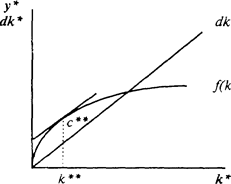
Это основное уравнение для накопления капитала. Интерпрета­ция его такова. Ежегодно в экономику поступает n рабочих сил. Обес­печивая каждую из них капиталом k, расходуем nk. Замена выбывше­го капитала требует расходов dk. Таким образом, для поддержания отношения K/L а постоянном уровне k требуется sy удельных сбере­жений. Экономика находится в стационарном состоянии (нет ни из­быточных сбережений, ни недостаточных инвестиций), когда Δk = 0. В этом случае 13) сводится к 7).

Подведем промежуточные итоги:

1. Для поддержания постоянного уровня капиталовооруженно­сти сбережения и инвестиции должны быть достаточными для того, чтобы компенсировать уменьшение величины капитала на одного ра­ботающего, обусловленное ростом населения и амортизацией.

2. Если S = sY, то капиталовооруженность стремится к стационар­ному уровню k*, при котором выпуск (а тем самым сбережения и инве­стиции) достаточен для поддержания k = const.

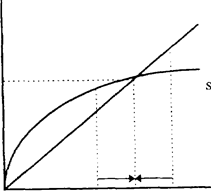
3. Достижение уровня k* обеспечивается тем, что при малых k верно S > I, обеспечивая Δk > 0 (при больших k верно S < I, создавая ^ < 0).

Отметим также, что в этой модели Солоу уровень (норма) сбе­режений не оказывает никакого влияния на темп роста в устойчивом состоянии, равный n. Независимо от того, каково s, в долгосрочном периоде экономика растет с темпом п. Однако уровень сбережений может влиять на время приближения к равновесию и на доход на ду­шу населения в долгосрочном устойчивом состоянии. Чем больше s, тем больше доход, но долгосрочный темп роста этого дохода не зави­сит от s (в предположении постоянной отдачи от масштаба и отсутст­вии НТП).

Это позволяет понять, что произойдет, если в стране возрастет уровень сбережений. С ростом уровня сбережений объем сбереже­ний начнет превышать потребности расширения капитала и величи­на K/L начинает расти. Возникает переходный период, когда темп роста экономики превышает n, поскольку ΔY/Y > ΔL/L= n. По ме­ре приближения к равновесию темп роста уменьшается до величи­ны п.

Таким образом, рост сбережений ведет к временному увеличе­нию темпов экономического роста и к росту уровня капиталовоору­женности. Однако окончательный темп экономического роста (темп роста в новом стационарном состоянии) по-прежнему будет равен п.

Другим фактором, определяющим темп экономического роста и величину Y/L, является темп роста населения (рабочей силы). При этом возникают двоякого рода изменения. Во-первых, более высо-кий темп роста населения способствует увеличению темпа долговре­менного экономического роста, поскольку в долгосрочном равнове­сии Y/ К и L увеличиваются темпом, равным темпу роста населения.

Во-вторых, темп роста населения определяет количество сбере­жений, направленных на расширение капитала (оно равно nk) Это ведет к уменьшению величины у = Y/L. Иными словами, при прочих равных условиях более высокий темп роста населения ведет к сниже­нию дохода на душу населения в устойчивом состоянии.

До сих пор мы предполагали, что ΔА/А = 0. Тогда, если n = 0, то экономический рост отсутствует. Однако технический прогресс воз­растающая отдача от масштаба и совершенствование человеческого капитала ведут к возможности экономического роста даже при n = 0.

Рассмотрим технологические изменения. Основное предположе­ние состоит в том, что они являются трудосберегающими: количест­во вложенного труда, измеряемого в неизменных величинах астро­номического времени, растет за счет улучшения качества услуг труда Соответственно производственная функция принимает вид-

Y=F(K,TL) (3)

Более высокий уровень технического прогресса, выражаемый ростом Т, означает просто увеличение вклада труда при неизменном L. Величина

Le = TL (4)

называется эффективным трудом. Из его определения (9) вид­но, что

ΔLe/ Le = ΔТ/Т + ΔL/L = n + o, (5)

где o = ΔТ/Т — темп технологических изменений. Темп роста эф­фективного труда равен n + o .

Таким образом, эффективный труд растет по двум каналам: за счет роста населения и за счет возрастания качества услуг труда. Поэтому технологические изменения увеличивают темп экономического роста в устойчивом состоянии. В этом состоянии выпуск на одного эффек­тивного рабочего и количество капитала на одного эффективного ра­ботающего не изменяются. Однако, если o > 0, то выпуск на одного реального рабочего и количество капитала на одного реального рабо­чего растут со скоростью o. Таким образом, скорость технологических изменений определяет темп роста Y/L в устойчивом состоянии, т е темп роста ВНП на душу населения. Вместо Y/L = const теперь в ус­тойчивом состоянии возникает равенство ΔY/L = const.

Прием замены простого труда эффективным в результате воздей­ствия НТП на производство можно распространить и на капитал. Тех­нологический прогресс рассматривается в этом случае не как само­стоятельный фактор производства, вклад которого в прирост выпуска измеряется «остатком Солоу», а в качестве силы, увеличивающей про­изводительность труда и капитала по сравнению с их базовой (исход­ной) производительностью.

Повышая эффективность факторов производства, технологиче­ский прогресс ведет не только к ускоренному экономическому рос­ту, но и к перераспределению национального дохода и изменению экономической конъюнктуры. Не менее важна и неопределенность, свя-эанная с определением эффективных значений труда и капитала. Невозможность их прямого представления в виде конкретных физи­ческих величин приводит к тому, что эффективный труд и эффек­тивный капитал могут быть измерены только в денежных единицах, причем само это измерение может быть осуществлено только в про­цессе функционирования финансового рынка, непрерывно коррек­тирующего денежные оценки. Это заставляет экономических субъ­ектов уделять событиям в мире денег все большее внимание.