Навигация
Математическая модель оценки показателей качества ДО
3. Математическая модель оценки показателей качества ДО.
3.1 Поглощающие марковские цепи
Как указывалось выше, у поглощающих ДМЦ имеется множество, состоящее из одного или нескольких поглощающих состояний.
Для примера рассмотрим переходную матрицу, описывающую переходы в системе, имеющей 4 возможных состояния, два из которых являются поглощающими. Матрица перехода такой цепи будет иметь вид:
 (1)
(1)
Практически важным является вопрос о том, сколько шагов сможет пройти система до остановки процесса, то есть поглощения в том или ином состоянии. Для получения дальнейших соотношений путем переименования состояний матрицу (1) переводят к блочной форме:
 (2)
(2)
![]()
Такая форма позволяет представить матрицу (2) в каноническом виде:
 (2а)
(2а)
где  - единичная матрица;
- единичная матрица;
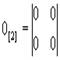 - нулевая матрица;
- нулевая матрица;
 - матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество;
- матрица, описывающая переходы в системе из невозвратного множества состояний в поглощающее множество;
 - матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний.
- матрица, описывающая внутренние переходы в системе в невозвратном множестве состояний.
На основании канонической формы (2а) получена матрица, называемая фундаментальной:
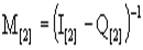 (3)
(3)
В матрице (3) символ (-1) означает операцию обращения, то есть
![]() (4)
(4)
После соответствующих преобразований матрица (3) примет вид:
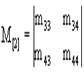 (3а)
(3а)
Каждый элемент матрицы (3а) соответствует среднему числу раз попадания системы в то или иное состояние до остановки процесса (поглощения).
Если необходимо получить общее среднее количество раз попадания системы в то или иное состояние до поглощения, то фундаментальную матрицу М необходимо умножить справа на вектор-столбец, элементами которого будут единицы, то есть
![]() (4а)
(4а)
где 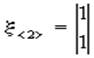 .
.
Для иллюстрации приведем конкретный числовой пример: пусть известны значения переходных вероятностей матрицы ![]() с одним поглощающим состоянием:
с одним поглощающим состоянием: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Переходная матрица в блочной системе будет выглядеть так:

В данном случае
![]() ;
; ![]() ;
;  ;
; 
Проделаем необходимые вычисления:
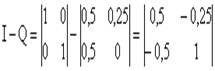 ;
;
 ;
;
 .
.
В данном случае компоненты вектора ![]() означают, что если процесс начинается с состояния
означают, что если процесс начинается с состояния ![]() , то общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния
, то общее среднее число шагов процесса до поглощения будет равно 3,34 и, соответственно, если процесс начинается с состояния ![]() , то - 2,26.
, то - 2,26.
В конкретных задачах, конечно, более информативным результатом будет не количество шагов, а какие-либо временные или экономические показатели. Этот результат легко получить, если связать пребывание в каждом состоянии с соответствующими характеристиками. Очевидно, набор этих характеристик составит вектор, на который нужно умножить ![]() слева.
слева.
Так, если задать в нашем примере время пребывания в состоянии ![]()
![]() , а в состоянии
, а в состоянии ![]() -
- ![]() , то общее время до поглощения будет равно:
, то общее время до поглощения будет равно:
![]()
В случаях, когда марковская цепь включает несколько поглощающих состояний, возникают такие вопросы: в какое из поглощающих состояний цепь попадет раньше (или позже); в каких из них процесс будет останавливаться чаще, а в каких - реже? Оказывается, ответ на эти вопросы легко получить, если снова воспользоваться фундаментальной матрицей.
Обозначим через ![]() вероятность того, что процесс завершится в некотором поглощающем состоянии
вероятность того, что процесс завершится в некотором поглощающем состоянии ![]() при условии, что начальным было состояние
при условии, что начальным было состояние ![]() . Множество состояний
. Множество состояний ![]() снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы - всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом:
снова образует матрицу, строки которой соответствуют невозвратным состояниям, а столбцы - всем поглощающим состояниям. В теории ДМЦ доказывается, что матрица В определяется следующим образом:
![]() (4.б)
(4.б)
где
М - фундаментальная матрица с размерностью S;
R - блок фундаментальной матрицы с размерностью r.
Рассмотрим конкретный пример системы с четырьмя состояниями ![]() , два из которых-
, два из которых- ![]() - поглощающие, а два -
- поглощающие, а два - ![]() - невозвратные (рис.10):
- невозвратные (рис.10):
![]()
Система с четырьмя состояниями
Для наглядности и простоты вычислений обозначим переходные вероятности следующим образом:
![]() ;
; ![]() ;
; ![]()
Остальные значения вероятностей будут нулевыми. Каноническая форма матрицы перехода в этом случае будет выглядеть так:

Фундаментальная матрица после вычислений примет вид:
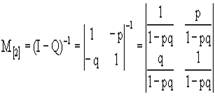
Тогда, согласно формуле (5), матрица вероятностей поглощения вычисляется так:
 .
.
Поясним вероятностный смысл полученной матрицы с помощью конкретных чисел. Пусть![]() , а
, а![]() . Тогда после подстановки полученных значений в матрицу
. Тогда после подстановки полученных значений в матрицу ![]() получим:
получим:
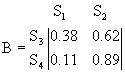
Таким образом, если процесс начался в ![]() , то вероятность попадания его в
, то вероятность попадания его в ![]() равна
равна ![]() , а в
, а в ![]() -
- ![]() . Отметим одно интересное обстоятельство: несмотря на то, что, казалось бы, левое поглощающее состояние (“левая яма”) находится рядом с
. Отметим одно интересное обстоятельство: несмотря на то, что, казалось бы, левое поглощающее состояние (“левая яма”) находится рядом с ![]() , но вероятность попадания в нее почти в два раза меньше, чем в “удаленную яму” -
, но вероятность попадания в нее почти в два раза меньше, чем в “удаленную яму” - ![]() . Этот интересный факт подмечен в теории ДМЦ, и объясняется он тем, что
. Этот интересный факт подмечен в теории ДМЦ, и объясняется он тем, что ![]() , то есть процесс имеет как бы “правый уклон”. Рассмотренная выше модель называется в теории ДМЦ моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр.
, то есть процесс имеет как бы “правый уклон”. Рассмотренная выше модель называется в теории ДМЦ моделью случайного блуждания. Такими моделями часто объясняются многие физические и технические явления и даже поведение игроков во время различных игр.
В частности, в рассмотренном примере объясняется тот факт, что более сильный игрок может дать заранее значительное преимущество (“фору”) слабому противнику и все равно его шансы на выигрыш будут более предпочтительными.
Кроме указанных выше средних характеристик вероятностного процесса с помощью фундаментальной матрицы можно вычислить моменты и более высоких порядков. В частности, дисперсия числа пребывания в том или ином состоянии - D определяется с помощью следующей матрицы:
![]() (6)
(6)
где
![]() - диагональная матрица, т.е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (3а) будет иметь вид:
- диагональная матрица, т.е. матрица, полученная из М путем оставления в ней лишь диагональных элементов и замены остальных элементов нулями. Например, приведенная выше матрица (3а) будет иметь вид:
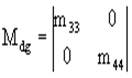
В свою очередь, матрица М представляет собой матрицу, полученную из М путем возведения в квадрат каждого ее элемента, то есть для (3а) будем иметь:

Аналогичным образом определяема и дисперсия для общего количества раз пребывания в том или ином состоянии ![]() . Обозначим ее
. Обозначим ее ![]() :
:

Похожие работы
... с положительностью сальдо поступлений и расходов и малым сроком окупаемости. 6. Обеспечение безопасности жизнедеятельности в системе ДО В данном дипломном проекте разработана автоматизированная информационная система дистанционного обучения по дисциплине “Финансы и кредит”. Ее использование тесно связано с применением ПЭВМ, поэтому организация рабочего места пользователя системы должна ...
... результаты отчета. Они являются кульминационным пунктом отчета и должны быть разумными, хорошо определенными, перечисленными и обоснованными [11].Практика дистанционного образования с использованием Internet Шутилов Ф.В. Особенности заочного образования - в необходимости обеспечить высокий уровень знаний при значительно меньшем времени непосредственного личного общения студентов с преподавателем. ...
... ). В России экономическая и технологическая ситуация такова, что выбор средств зависит не от их педагогического потенциала и даже не от их стоимости, а от их распространенности. Телекоммуникации добавляют новую размерность к дистанционному обучению и очень быстро развиваются в России в виде применения асинхронной электронной почты. Проведенный анализ позволил выделить базовые параметры, которые ...
... лишь прагматическими представителями значительно более широкого перечня алгоритмов, применяющихся в планировании и других экономических расчетах. IV. Заключение Как видно из всего вышесказанного, значение математических моделей и информатики в управлении велико. В ближайшие 10 лет мир изменится сильнее, чем за предыдущие 50. И от того, насколько правильно мы сможем организовать свою жизнь, ...
0 комментариев