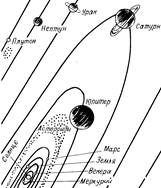
Рис. 1. Солнечная система
Солнечная система включает девять крупных планет, которые со своими 57 спутниками обращаются вокруг массивной звезды по эллиптическим орбитам. По своим размерам и массе планеты можно разделить на две группы: планеты земной группы, расположенные ближе к Солнцу, - Меркурий, Венера, Земля и Марс и планеты-гиганты - Юпитер, Сатурн, Уран и Нептун, находящиеся на значительно более удаленных от центральной звезды орбитах. Последняя из известных планет - Плутон - своей орбитой с радиусом около 6 млрд. км очерчивает границы Солнечной системы. Плутон не относится к планетам-гигантам, его масса почти в 10 раз меньше массы Земли. Аномальные характеристики этой крошечной планеты позволяют рассматривать ее как бывший спутник Нептуна.
Кроме больших планет между орбитами Марса и Юпитера вращается более 2300 малых планет - астероидов, множество более мелких тел - метеоритов и метеорной пыли, а также несколько десятков тысяч комет, двигающихся по сильно вытянутым орбитам, некоторые из которых далеко выходят за границы Солнечной системы.
Все планеты и астероиды обращаются вокруг Солнца в направлении движения Земли - с запада на восток. Это так называемое прямое движение. Основные закономерности движения планет полностью определяются законами Кеплера. Рассмотрим эти законы и охарактеризуем основные элементы эллиптических орбит.
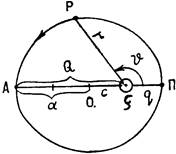
Рис. 2. Элементы планетной орбиты: АП - большая полуось орбиты, ось апсид; П - перегилий; А - афелий;
r - радиус-вектор
Согласно первому закону, все планеты обращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. На рис. II.2 показаны элементы планетных орбит с Солнцем (С) в фокусе. Линия АП называется линией апсид, крайние точки которой афелий (А) и перигелий (П) характеризуют наибольшее и наименьшее удаление от Солнца. Расстояние планет (Р) на орбите от Солнца (гелиоцентрическое расстояние) определяется радиусом-вектором r=СР. Отношение полуфокального расстояния (с) к большой полуоси (а) называется эксцентриситетом орбиты:
e = 
. (II.1)
Если обозначить через q перигельное расстояние, а через Q - афелийное расстояние, то их значения легко определить из выражений:
q = а - с = а(1 - е), (II.2)
Q = а + с = а(1 + е). (II.3)
Тогда, определив большую полуось (а), мы найдем среднее годичное расстояние планеты до Солнца:
а = 
. (II.4)
Cреднее гелиоцентрическое расстояние Земли от Солнца равно 149,6 млн. км. Эта величина называется астрономической единицей и принимается за единицу измерений расстояний в пределах Солнечной системы.
Согласно второму закону Кеплера, радиус-вектор планеты описывает площади, прямо пропорциональные промежуткам времени. Если обозначить через S1 площадь перигелийного сектора (рис. II.3), а через S2 - площадь афелийного сектора, то их отношение будет пропорционально временам t1 и t2, за которые планета прошла соответствующие отрезки дуг орбиты:
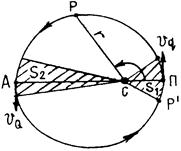
Рис. 3. Площади, описываемые радиус-вектором планеты
= 
. (II.5)
Отсюда следует, что секториальная скорость -
V = 
= 
= const - (II.6)
величина постоянная.
Время, в течение которого планета сделает полный оборот по орбите, называется звездным, или сидерическим, периодом Т (рис. II.3). За полный оборот радиус-вектор планеты опишет площадь эллипса:
S= pab=p a2 
. (II.7)
Поэтому секториальная скорость
V = 
= 
(II.8)
оказывается наибольшей в перигелии, а наименьшей - в афелии. Используя второй закон, можно вычислить эксцентриситет земной орбиты по наибольшему и наименьшему суточному смещению Солнца по эклиптике, отражающему движение Земли (см. § 2). Земля в перигелии пребывает в начале января (hmax=61'), а в афелии в начале июля (hmax=57'). По второму закону Кеплера скорость Земли в афелии и перигелии определяется из выражений:
VQ=hminQ, Vq=hmaxq. (II.9)
Учитывая закон сохранения момента количества движения
Vq· q = VQ· Q (II.10)
и подставив сюда значения (II.9) с учетом выражений (II.2) и (II.3), найдем:
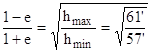= 1,03397, откуда е=0,0167.
Таким образом, орбита Земли лишь ненамного отличается от окружности.
Согласно третьему Закону Кеплера, квадраты сидерических периодов обращения планет (Т12 и Т22) прямо пропорциональны кубам их средних расстояний от Солнца (а13 и а23):
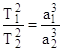. (II.11)
Если одна из планет - Земля, период ее сидерического обращения равен Т1=1 году, а расстояние от Солнца а1 положить равным а1=1 а. е., то выражение (II.11) принимает простой вид:
Т22 = а23. (II.12)
Полученное выражение позволяет по известным из наблюдений периодам обращения планет, других небесных тел вокруг Солнца вычислять их средние гелиоцентрические расстояния.
Найденные эмпирически из наблюдательной астрономии законы Кеплера показали, что Солнечная система представляет собой механическую систему с центром, находящимся в солнечной массе.
Законы Кеплера послужили Ньютону основой для вывода своего знаменитого закона всемирного тяготения, который он сформулировал так: каждые две материальные частицы взаимно притягиваются с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
Математическая формулировка этого закона имеет вид:
F = G
, (II.13)
где M и m - взаимодействующие массы, r - расстояние между ними, G - гравитационная постояная. В системе СИ G = 6,672· 10-11 м2· кг-1· с-2. Физический смысл гравитационной постоянной заключается в следующем: она характеризует силу притяжения двух масс весом в 1 кг каждая на расстоянии в 1 м. Величина G впервые была определена в 1798 г. английским физиком Кавендишем с помощью крутильных весов.
Закон Ньютона решил задачу о характере действия силы, управляющей движением планет. Это сила тяготения, создаваемая центральной массой Солнца. Именно эта сила не дает планетам разлететься, а сохраняет их в связной системе последовательных орбит, по которым, как на привязи, сотни миллионов лет кружатся большие и малые планеты.
Решая задачу движения двух тел под действием взаимного притяжения, Ньютон аналитически определил законы движения планет в поле тяготения Солнца. Тем самым эмпирические законы Кеплера получили строгое математическое доказательство. Третий же закон был уточнен путем введения масс планет и Солнца:
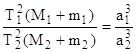. (II.14)
Теперь с его помощью оказалось возможным вычислять массы небесных тел. Полагая в выражении (II.14) массы спутников планет m1 и m2 равными нулю (ввиду их малости в сравнении с массой планет, за исключением Луны) и приняв массу Земли M2 = 1, получим соотношение (II.14) следующего вида:
= М1. (II.15)
Воспользуемся законом тяготения и определим массу Земли, полагая, что взаимодействуют две массы - Земли (М) и некоторого тела, лежащего на ее поверхности. Сила притяжения этого тела определяется законом Ньютона:
F = G
. ( II.16)
Но одновременно из второго закона механики эта же сила равна произведению массы на ускорение:
F = mg, (II.17)
где g - ускорение силы тяжести; R - радиус Земли.
Приравнивая правые части выражений (II.16) и (II.17): G = mg, найдем выражение для определения массы Земли:
М = 
. (II.18)
Подставив в (II.18) известные значения G = 6,672 · 10-11 м2 · кг-1 · с-2, g = 9,81 м/с2, R = 6,371 · 106 м, в итоге получим M3 = 5,97 · 1024 кг, или в граммах: M3 = 5,97 · 1027 г. Такова масса Земли. Обращаем внимание на формулы (II.16), (II.17), (II.18) - их надо твердо помнить. В дальнейшем мы часто будем пользоваться ими как исходными для определения входящих в них параметров.
Теперь воспользуемся уточненным третьим законом Кеплера и найдем из выражения (II.15) массу Солнца. Для этого рассмотрим две системы тел - Солнце с Землей и Землю с Луной. В первой системе a1 = 149,6 · 106 км, Т1 = 365,26 сут; во второй системе а2 = 384,4·103 км, Т2 = 27,32 сут. Подставляя эти значения в формулу (II.15), находим массу Солнца в относительных единицах массы Земли М0 = 328700 М3. Полученный результат отличается от более точных расчетов, так как в сравнении с массой Земли массу Луны нельзя приравнивать к нулю (масса Луны составляет 1/81 массы Земли). Зная массу Земли в абсолютных единицах (килограммах или граммах) и взяв более точное определение массы Солнца (М0 = 333000 М3), определим его абсолютную массу: М0 = 333000·5,97·1027 г = 1,98·1033 г.
В настоящее время для более точного определения массы и фигуры планет и их спутников используются параметры орбиты искусственных спутников, запускаемых с Земли.
Список литературы
Для подготовки данной работы были использованы материалы с сайта http://www.i-u.ru/
Похожие работы
... в 1609, раскрывают характер движения каждой планеты по отдельности, что не удовлетворило Кеплера. Он продолжил поиски «гармонии» в движении всех планет, и спустя 10 лет ему удалось сформулировать третий закон Кеплера. Квадраты звёздных периодов обращения планет относятся между собой как кубы больших полуосей их орбит. Формула, выражающая третий закон Кеплера, такова: A13 ...
... или гравитационными силами. И так: между телом и Землей, между планетами и Солнцем, между Луной и Землей действуют силы всемирного тяготения, обобщенные в закон. ТЕМА. ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ. В ходе занятия мы будем использовать знания истории физики, астрономии, математики, законы философии и сведения из научно-популярной литературы. Познакомимся с историей открытия закона всемирного ...
... , это наличные деньги, т.е. агрегат МО. А самые неликвидные – это большие долгосрочные вклады и ценные бумаги, их содержат агрегаты М3 и L. 2.1 Особенности денежного обращения в современной экономике США и России (содержание) Денежный агрегат M1 - в США - наиболее узкая мера денежного предложения, включающая, вклады не являющиеся собственностью федерального правительства, ...
... цессами, происходящими на поверхности планеты, или конкретнее, что тут мы имеем дело с проявлением вулканической деятельности. В связи с этим необходимо пересмотреть модель внутреннего строения планет-гигантов. Что же касается окончательного выяснения механизма происхождения низкочастотного радиоизлучения Юпитера, то ответ на этот вопрос следует отнести к будущему. Теперь же можно сказать лишь ...
0 комментариев