Халфина А.А.
Известно, что в некоторых магнитоупорядоченных кристаллах образуется длиннопериодическая магнитная структура, называемая сверхструктурой. В простейшем случае сверхструктуры вектор плотности магнитного момента поворачивается вокруг избранной оси так, что конец вектора вычерчивает в пространстве геликоид. Теория геликоидальных структур (ГС) в антиферромагнетиках (АФМ) построена И.Е.Дзялошинским [1]. Показано, что их существование может быть связано с наличием в свободной энергии линейных по пространственным производным слагаемых. Так, например, сверхструктура одноосных АФМ обусловлена инвариантом лифшицевского вида l(ly×дlx/дz-lx×дly/дz). Здесь l - вектор антиферромагнетизма, ось z направлена вдоль оси анизотропии. Такой инвариант допускает кристаллографический класс Cn, и ГС является «врожденным» свойством этих АФМ. При наличии внешних магнитного H и электрического E полей появление таких слагаемых в свободной энергии с l=l0Ez или l=l0Hz возможно и в АФМ иной симметрии, т.е. ГС можно индуцировать полями H и E [2, 3].
Магнитная симметрия АФМ с магнитоэлектрическим эффектом допускает линейный неоднородный обменный инвариант Dmдl/дz [4], где m - вектор ферромагнетизма. Статические свойства таких АФМ и линейные возбуждения в них без учета вышеуказанного инварианта изучены достаточно подробно (см. напр. [5-7]). Нами показано сильное влияние этого инварианта на формирование доменной структуры центроантисимметричных АФМ в магнитном поле [8]. В настоящем сообщении обсуждается возможность индуцирования длиннопериодической структуры в АФМ с магнитоэлектрическим эффектом.
Рассмотрим двухподрешеточный ромбоэдрический центроантисимметричный АФМ со структурой ![]() . Исходим из плотности свободной энергии
. Исходим из плотности свободной энергии
F=Fm+Fmp+Fp,
включающей магнитную, магнитоэлектрическую энергии и энергию электрической поляризации. В приближении ml=0, m2+l2=1 каждое из слагаемых энергии имеет следующий вид [4, 7]:
![]()
![]() ,
, ![]() .
.
Здесь ![]() - константа однородного обмена, c - поперечная антиферромагнитная восприимчивость,
- константа однородного обмена, c - поперечная антиферромагнитная восприимчивость, ![]() , D~Ba0 - константы квадратичного и линейного неоднородного обмена, a0 - постоянная кристаллической решетки; a>0, a1<0 - константы магнитной анизотропии,
, D~Ba0 - константы квадратичного и линейного неоднородного обмена, a0 - постоянная кристаллической решетки; a>0, a1<0 - константы магнитной анизотропии, ![]() – тензор магнитоэлектрического взаимодействия,
– тензор магнитоэлектрического взаимодействия, ![]() , кz – компоненты тензора электрической поляризуемости, p – вектор электрической поляризации.
, кz – компоненты тензора электрической поляризуемости, p – вектор электрической поляризации.
Свободную энергию в полях H<<HE=B/4M0 после минимизации по p и m можно представить в виде
|
| (1) |
Нp=[(g1ly+g3lz)Ex+g1lxEy, g1lxEx+(g3lz-g1ly)Ey, g2(Exlx+Eyly)-g0Ezlz].
Здесь для краткости принято ![]()
Пусть H || z, E || x, l=(sinqcosj, sinqj, cosq). Рассмотрим случай одномерной неоднородности вдоль оси z. Тогда плотность энергии (1) примет вид:
|
| (2) |
где A*=A(1-m2), m2=D2/AB, a*=a-cH2.
Для простоты рассмотрим случай A*>0 и a1=-a*, соответствующий полю спин-флоп перехода. В отсутствие полей H и E решение уравнения Эйлера для угла j дает значение j=const. Сделав замену q=p/4-n/2, получим:
|
| (3) |
Уравнение Эйлера для функционала (3) имеет первый интеграл
| A*(dv/dz)2+|a1|sin2v=|a1|/k2. | (4) |
Решение уравнения (4) имеет вид:
| cos2q=sn(kz/d, k), | (5) |
где sn(u, k) - эллиптическая функция Якоби, ![]() - характерный размер магнитной неоднородности. Выражение (5) описывает геликоид вектора l , иначе - модуляцию чисто антиферромагнитного состояния q=0, p или q=p/2, 3p/2 (спины вдоль 3z или 2х-осей), поэтому называется еще модулированной магнитной структурой (ММС).
- характерный размер магнитной неоднородности. Выражение (5) описывает геликоид вектора l , иначе - модуляцию чисто антиферромагнитного состояния q=0, p или q=p/2, 3p/2 (спины вдоль 3z или 2х-осей), поэтому называется еще модулированной магнитной структурой (ММС).
Из (2) с учетом (4), (5) получим прирост энергии, обусловленный ММС:
|
| (6) |
|
| (7) |
где K(k) и E(k) – полный эллиптический интеграл I и II рода соответственно; a=cg – магнитоэлектрическая восприимчивость. Из (6) и (7) видно, что плоскость геликоида фиксируется линейным неоднородным обменом. Положим для определенности k0>0. Тогда минимуму (6) соответствует значение j=0 .
Модуль эллиптического интеграла k, а вместе с ним и период структуры L=4Kkd можно определить из условия минимума энергии (6) по k. Рассмотрим два случая, соответствующие предельным значениям k®0 и k®1.
Используя разложения E(k) и K(k) при малых k, имеем:
![]()
Условие dF/dk=0 удовлетворяется значением ![]() . Прирост энергии равен
. Прирост энергии равен
|
| (8) |
а период структуры
|
| (9) |
Из условия k<1 следует, что ММС в рассматриваемых АФМ может возникнуть, только если поле Е превышает пороговое значение Еп (7), величина которого вблизи спин-флоп фазового перехода определяется константой анизотропии четвертого порядка и магнитоэлектрической восприимчивостью. Это связано с тем, что инвариант Dmдl/дz имеет существенно нелифшицевский вид, а индуцирование ММС электрическим полем происходит через механизм магнитоэлектрического взаимодействия.
В случае k®1 km=1+2b/lnb, где b=p/2k0-1<<1. Прирост энергии, обусловленный наличием ММС, равен
|
| (10) |
Период структуры ![]() , величина L/d=2|lnb|>>1, и теперь (5) описывает периодическую структуру с узкими переходными слоями, в которых вектор антиферромагнетизма l меняет направление на p/2. В отличие от обычной доменной структуры прирост энергии ММС относительно однородного состояния (10) отрицателен, т.е. ММС энергетически выгодна.
, величина L/d=2|lnb|>>1, и теперь (5) описывает периодическую структуру с узкими переходными слоями, в которых вектор антиферромагнетизма l меняет направление на p/2. В отличие от обычной доменной структуры прирост энергии ММС относительно однородного состояния (10) отрицателен, т.е. ММС энергетически выгодна.
Проведенные исследования показывают, что условием существования длиннопериодической магнитной структуры в антиферромагнетиках с магнитоэлектрическим эффектом является малость анизотропии (чему может способствовать близость к точкам фазового перехода) и большая величина магнитоэлектрической восприимчивости материала.
Список литературы1. Дзялошинский И.Е. // ЖЭТФ. 1964. Т. 47. № 3 (9). С. 992–1003.
2. Витебский И.М. // ЖЭТФ. 1982. Т. 82. № 2. С. 57–361.
3. Барьяхтар В.Г., Яблонский Д.А. // ФТТ. 1982. Т. 24. № 8. С. 2522–2524.
4. Шавров В.Г. // ЖЭТФ. 1965. Т. 48. С. 1419–1426.
5. Tankeyev A.P., Shamsutdinov M.A., Kharisov A.T. // J.Phys.: Condens. Matter. 2000. V. 12. P. 1053–1064.
6. Харрасов М.Х., Абдулин А.У. // ДАН. 1994. Т. 336. С. 335–337. 7. Туров Е.А.// ЖЭТФ. 1993. Т. 104. № 5. С. 3886–3896.
Khalfina A.A., Shamsutdinov M.A.// Abstract Book. EASTMAG-2001. Ekaterinburg, 2001. P.
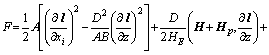
0 комментариев