Абзалимов Р.Р.
В настоящей работе предлагается метод расчета приближенных собственных чисел и собственных функций краевой задачи на полуоси для дифференциального уравнения второго порядка. Для численного расчета собственных чисел интервал ![]() заменяется на
заменяется на ![]() , после чего задача решается на конечном отрезке. Точность приближенных собственных чисел будет зависеть от выбора граничного условия в точке R.
, после чего задача решается на конечном отрезке. Точность приближенных собственных чисел будет зависеть от выбора граничного условия в точке R.
I. Регулярная задача
Рассмотрим следующую краевую задачу:
![]() , (1.1)
, (1.1)
![]() , (1.2)
, (1.2)
![]() . (1.3)
. (1.3)
Здесь предполагается, что q(x) кусочно-непрерывна на [a, b]. Наряду с данной задачей рассмотрим дифференциальные операторы вида:
![]() , (1.4)
, (1.4)
![]()
с граничными условиями
![]() , (1.5)
, (1.5)
![]() , (1.6)
, (1.6)
где
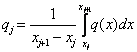 .
(1.7)
.
(1.7)
Под собственными функциями краевой задачи (1.4)-(1.6) будем понимать функцию y(x), удовлетворяющую следующим условиям (см. [1]):
![]() ;
;
![]() ;
;
![]() удовлетворяет граничным условиям (1.5) и (1.6);
удовлетворяет граничным условиям (1.5) и (1.6);
![]() удовлетворяет так называемым условиям сопряжения
удовлетворяет так называемым условиям сопряжения
![]() (1.8)
(1.8)
В каждом интервале ![]() решения
решения ![]() уравнения (1.4) имеют вид:
уравнения (1.4) имеют вид:
![]() . (1.9)
. (1.9)
Из условий сопряжения (1.8) и (1.9) имеем:
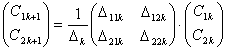 , (1.10)
, (1.10)
где ![]() ,
, ![]() выписываются явно (i=1,2; j=1,2; k=1..N). Таким образом, получаем:
выписываются явно (i=1,2; j=1,2; k=1..N). Таким образом, получаем:
 (1.11)
(1.11)
Из первого краевого условия получаем зависимость ![]() от
от ![]() , затем, подставляя во второе краевое условие (1.6), получаем уравнение для собственных значений задачи (1.4)-(1.6):
, затем, подставляя во второе краевое условие (1.6), получаем уравнение для собственных значений задачи (1.4)-(1.6):
![]() , (1.12)
, (1.12)
где ![]() выписывается явно.
выписывается явно.
Пусть ![]() - собственные значения и
- собственные значения и ![]() - соответствующие им собственные функции задачи (1.4)-(1.6), где через h обозначено
- соответствующие им собственные функции задачи (1.4)-(1.6), где через h обозначено
![]() ,
,
и пусть![]() - собственные значения задачи (1)-(3) и
- собственные значения задачи (1)-(3) и ![]() соответствующие им собственные функции. Введем обозначение:
соответствующие им собственные функции. Введем обозначение:
![]() . (1.13)
. (1.13)
Заметим прежде, что ![]() при
при ![]() .
.
Тогда имеет место следующая
ТЕОРЕМА 1.1 Справедливы равенства
![]() , (1.14)
, (1.14)
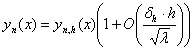 . (1.15)
. (1.15)
Доказательство. Вначале докажем равенство (1.15). Для этого рассмотрим уравнение (1.1) на интервале ![]() . Представим ее в виде
. Представим ее в виде
![]() , (1.16)
, (1.16)
где ![]() вычисляется по формуле (1.7). Для уравнения (1.16) получаем интегральные уравнения:
вычисляется по формуле (1.7). Для уравнения (1.16) получаем интегральные уравнения:
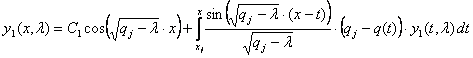 ,
,
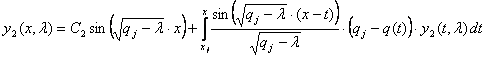 .
.
Применяя метод последовательных приближений, получаем:
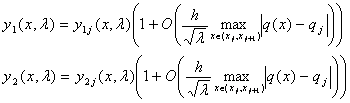 , (1.17)
, (1.17)
где ![]() - решения уравнения (1.4).
- решения уравнения (1.4).
Следовательно, для всего промежутка [0,p] справедливо равенство (1.15).
Из (1.15) нетрудно установить неравенство:
![]() , (1.18)
, (1.18)
где ![]() при
при ![]() .
.
Тогда имеет место следующее равенство:
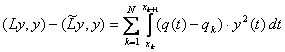 (1.19)
(1.19)
при ![]() , где
, где ![]() - оператор Штурма-Лиувилля задачи (1.1)-(1.3), а
- оператор Штурма-Лиувилля задачи (1.1)-(1.3), а ![]() - оператор задачи (1.4)-(1.6). Из (1.18) и (1.19) нетрудно показать справедливость оценки (1.14). Теорема доказана.
- оператор задачи (1.4)-(1.6). Из (1.18) и (1.19) нетрудно показать справедливость оценки (1.14). Теорема доказана.
Следствие 1.1 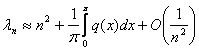 ,
,
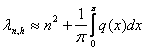 .
.
Следствие 1.2 ![]() , где
, где ![]() - характеристическое уравнение для собственных значений задачи (1.4)-(1.6),
- характеристическое уравнение для собственных значений задачи (1.4)-(1.6), ![]() - характеристическое уравнение для собственных значений задачи (1.1)-(1.3).
- характеристическое уравнение для собственных значений задачи (1.1)-(1.3).
Следствие 1.3 ![]() и
и ![]() совпадают со всеми корнями уравнения
совпадают со всеми корнями уравнения ![]() .
.
Следствие 1.4 ![]() образуют полную систему собственных функций.
образуют полную систему собственных функций.
II. Сингулярная задача. Случай ![]() .
.
Будем рассматривать задачу
![]() , (2.1)
, (2.1)
![]() , (2.2)
, (2.2)
где ![]() монотонно, т.е. уравнение (2.1) имеет не более одной точки поворота. Таким образом, для любого
монотонно, т.е. уравнение (2.1) имеет не более одной точки поворота. Таким образом, для любого ![]() . В случае, когда
. В случае, когда ![]() , спектральная задача имеет дискретный спектр. Из представленного метода решения регулярной задачи следует, что
, спектральная задача имеет дискретный спектр. Из представленного метода решения регулярной задачи следует, что ![]() ; таким образом, для каждого
; таким образом, для каждого ![]() задачи на полуоси ставится в соответствие своя регулярная задача на конечном отрезке
задачи на полуоси ставится в соответствие своя регулярная задача на конечном отрезке ![]() . Если бы мы знали все значения собственных функций
. Если бы мы знали все значения собственных функций ![]() , соответствующие собственным числам
, соответствующие собственным числам ![]() задачи на полуоси, в точке
задачи на полуоси, в точке ![]() , то, решая задачи на конечном промежутке
, то, решая задачи на конечном промежутке ![]() с дополнительным граничным условием
с дополнительным граничным условием ![]() , мы могли бы вычислить все собственные числа задачи на
, мы могли бы вычислить все собственные числа задачи на ![]() достаточно точно. Исходя из сказанного, можно утверждать, что погрешность определения собственных чисел тем меньше, чем точнее выбор второго краевого условия. В связи с этим рассмотрим два краевых условия
достаточно точно. Исходя из сказанного, можно утверждать, что погрешность определения собственных чисел тем меньше, чем точнее выбор второго краевого условия. В связи с этим рассмотрим два краевых условия ![]() (условие Дирихле) и
(условие Дирихле) и ![]() (условие Неймана). Пусть
(условие Неймана). Пусть ![]() - собственные числа задач на конечном промежутке с дополнительными условиями Дирихле и Неймана соответственно. С помощью метода решения регулярной задачи доказываются следующие утверждения:
- собственные числа задач на конечном промежутке с дополнительными условиями Дирихле и Неймана соответственно. С помощью метода решения регулярной задачи доказываются следующие утверждения:
ТЕОРЕМА 2.1 Справедлива асимптотическая формула собственных чисел задачи на полуоси
 , (2.3)
, (2.3)
где 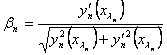 [1] .
[1] .
Справедливость теоремы 2.1 следует из следствия 1.1.
ТЕОРЕМА 2.2 Справедливо неравенство:
![]() .
(2.4)
.
(2.4)
Доказательство теоремы 2.2 можно провести с помощью функций распределения собственных чисел (см. [2]) или с помощью метода, предложенного в первой части работы, и следствия 1.1.
Замечание В случае полуограниченного оператора (![]() ), данный выбор краевых условий позволяет получать лишь верхнюю и нижнюю оценку собственных чисел.
), данный выбор краевых условий позволяет получать лишь верхнюю и нижнюю оценку собственных чисел.
Следствие 2.1 ![]() , где
, где ![]() - длина промежутка
- длина промежутка ![]() .
.
Пример
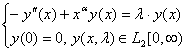 .
.
Известно, что ![]() , где
, где ![]() вычисляется явно. Из следствия 2.1 следует:
вычисляется явно. Из следствия 2.1 следует:
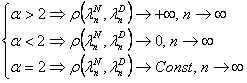 .
.
III. Сингулярная задача. Случай ![]() .
.
Будем рассматривать задачу
![]() , (2.1)
, (2.1)
![]() . (2.2)
. (2.2)
Имеет место следующая (см. [3])
ТЕОРЕМА 3.1 Пусть потенциальная функция ![]() удовлетворяет следующим условиям
удовлетворяет следующим условиям
![]() ;
;
![]() , при
, при ![]() ;
;
![]() сохраняет знак для больших
сохраняет знак для больших ![]() ;
;
![]() , где
, где ![]() , при
, при ![]() ;
;
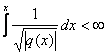 .
.
Тогда спектр оператора ![]() - чисто дискретный и состоит из двух серий собственных чисел, уходящих на
- чисто дискретный и состоит из двух серий собственных чисел, уходящих на ![]() и
и ![]() .
.
Аналогично (как и для полуограниченного оператора) задача на полуоси для расчета собственных чисел ![]() заменяется на регулярную задачу, т.е. интервал
заменяется на регулярную задачу, т.е. интервал ![]() заменяется на
заменяется на ![]() , где
, где ![]() - достаточно большое положительное число с дополнительным краевым условием
- достаточно большое положительное число с дополнительным краевым условием ![]() . Нетрудно установить, что погрешность приближенных собственных чисел неполуограниченного оператора (при
. Нетрудно установить, что погрешность приближенных собственных чисел неполуограниченного оператора (при ![]() ) стремится к нулю при
) стремится к нулю при ![]() . С помощью решения регулярной задачи доказывается следующая
. С помощью решения регулярной задачи доказывается следующая
ТЕОРЕМА 3.2 Пусть выполнены все условия теоремы 3.1. Тогда если ![]() - собственные числа задачи (2.1)-(2.2) на конечном промежутке
- собственные числа задачи (2.1)-(2.2) на конечном промежутке ![]() с дополнительным краевым условием
с дополнительным краевым условием ![]() , то справедливо равенство
, то справедливо равенство ![]() для всех
для всех ![]() .
.
Замечание 1 Известны более общие условия дискретности спектра задачи (2.1)-(2.2) (см. например [4]).
Замечание 2 Для расчета собственных чисел ![]() задачи (2.1)-(2.2), промежуток
задачи (2.1)-(2.2), промежуток ![]() заменяется на
заменяется на ![]() , где
, где ![]() - достаточно большое положительное число, с краевыми условиями
- достаточно большое положительное число, с краевыми условиями ![]() и
и ![]() .
.
IV. Сингулярная задача. Случай ![]() .
.
Будем рассматривать задачу
![]() , (3.1)
, (3.1)
![]() (3.2)
(3.2)
с дополнительными условиями:
![]() ;
;
![]() голоморфна в точке
голоморфна в точке ![]() , причем
, причем ![]() ;
;
![]() при
при ![]() монотонно, и
монотонно, и ![]() , где
, где ![]() ;
;
![]() при
при ![]() ,
, ![]() .
.
Данная задача рассматривалась в работе Е.ПЖидкова. и А.Г.Соловьева (см. [5]). Известно, что задача имеет собственные числа и собственные функции такие, что все ее собственные числа простые, отрицательные и образуют бесконечно возрастающюю последовательность ![]() с единственной предельной точкой
с единственной предельной точкой ![]() , а собственные функции
, а собственные функции ![]() , отвечающие собственным значениям
, отвечающие собственным значениям ![]() , имеют в интервале
, имеют в интервале ![]() в точности
в точности ![]() нулей. В этом случае справедливы все результаты, полученные для случая полуограниченного оператора.
нулей. В этом случае справедливы все результаты, полученные для случая полуограниченного оператора.
Пример
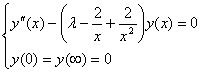 .
.
Известно (см. [3]), что ![]() - собственные числа.
- собственные числа.
Введем обозначения: ![]() - приближенные собственные числа, полученные Е.П.Жидковым и А.Г.Соловьевым, а
- приближенные собственные числа, полученные Е.П.Жидковым и А.Г.Соловьевым, а ![]() - приближенные собственные числа, полученные методом, описанным выше. Были рассчитаны собственные числа, которые представлены в таблице (см. ниже). Используя асимптотическую формулу (2.3), можно показать (достаточно грубая оценка), что
- приближенные собственные числа, полученные методом, описанным выше. Были рассчитаны собственные числа, которые представлены в таблице (см. ниже). Используя асимптотическую формулу (2.3), можно показать (достаточно грубая оценка), что
![]() ,
,
где ![]() вычисляется явно. Для более точной асимптотики необходимо точно решить уравнение
вычисляется явно. Для более точной асимптотики необходимо точно решить уравнение
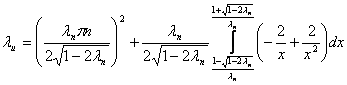 .
.
| n |
|
|
| Промежуток | ||
|
|
|
| ||||
| 1 | 0.2500 | 0.25000… | 0.247… |
|
| (1.16,6.82) |
| 2 | 0.1111 | 0.11107… | 0.111… |
|
| (1.06,16.9) |
| 3 | 0.0625 | 0.06249… | 0.063… |
|
| (1.03,30.9) |
| 4 | 0.0400 | 0.39995… | 0.041… |
|
| (1.02,48.9) |
| 5 | 0.0277 | 0.0277715 | 0.028… |
|
| (1.01,70.9) |
Митрохин С.И. // ДАН. 1997. Т. 356. № 1. С. 13-15.
Рид, Саймон. Методы современной математической физики. М.: Мир, 1977. Т. 1, 4
Титчмарш. Разложения по собственным функциям, связанные с дифференциальными уравнениями второго порядка. Т. 1. М.: Наука, 1960. 276 с.
Султанаев Я.Т. // ДАН. 1984. Т. 276. № 5. С. 1072-1074.
Жидков Е.П., Соловьев А.Г. // ЖВММФ. 1999. Т. 39. № 3. С. 1098-1
0 комментариев