Е.Г. Атавин, Омский государственный университет, кафедра органической химии
1. ВведениеИнтерес к геометрическому строению циклических молекул, интенсивно изучаемых как экспериментальными, так и расчетными методами, определяется не только их важнейшей ролью в органической химии и биохимии, но также сложностью и практически неисчерпаемым количеством соответствующих конформационных вариантов, особенно в случае гетероциклических соединений. Для построения модели (т.е. вычисления 3N декартовых координат) N-атомной молекулы в общем случае достаточно задать 3N-6 значений структурных параметров - межъядерных расстояний, валентных углов и углов внутреннего вращения, называющихся также внутренними или естественными переменными и легко оценивающихся по имеющимся эмпирическим закономерностям [1]. Оставшиеся 6 степеней свободы связаны с выбором положения и ориентацией молекулы в пространстве. Тем не менее, число структурных параметров, описывающих строение N-атомных моноциклических молекул, равно 3N (N межъядерных расстояний, N валентных углов и N углов внутреннего вращения). Из этих параметров лишь 3N-6 являются независимыми, и их значения можно выбирать произвольно (в пределах условия замыкания цикла). Оставшиеся 6 параметров называются зависимыми и определяются значениями независимых параметров.
Отметим, что пространственное строение нециклических молекул полностью описывается заданием значений N-1 межъядерных расстояний, N-2 валентных углов и N-3 углов внутреннего вращения. Замыкание цепи атомов в цикл увеличивает на единицу количество независимых межъядерных расстояний. При этом количество независимых угловых переменных уменьшается и становится недостаточным для непосредственного использования ранее рассмотренных алгоритмов построения нециклических молекул [2].
Алгоритмы построения циклических молекул по естественным переменным можно разделить на две группы.
Для итерационных методов (методы "стягивающего потенциала" и Шераги) характерна слабая чувствительность к качеству стартового приближения значений структурных параметров. Однако низкое быстродействие делает их малоэффективными при решении задач, требующих многократного построения модели молекулы (решение обратной задачи при поиске структурных параметров в дифракционных методах исследования, уточнение геометрии в методах молекулярной механики и квантовой химии, конформационный поиск и т.д.).
Алгоритмы построения геометрической модели молекулы неитерационными методами (метод Нордландера) опираются на вспомогательные геометрические построения, отличаются способом выбора 3N-6 назависимых параметров из общего их количества, работают значительно быстрее методов первой группы, однако требуют аккуратного выбора значений независимых геометрических параметров, не противоречащих условию замыкания цикла.
При сравнении алгоритмов полезно иметь в виду, что точность задания структурных параметров на основании эмпирических закономерностей существенно падает в ряду "межъядерные расстояния", "валентные углы", "торсионные углы", и включение в число зависимых параметров максимального количества торсионных углов является предпочтительным.
2. Метод "стягивающего потенциала" [3]
Очевидно, что линейная цепь атомов может быть неотличима от циклической, если подобрать соответствующие значения геометрических параметров. Подбор осуществляется итерационно, так, чтобы расстояние между концами линейной цепочки атомов постепенно приближалось к длине соответствующей химической связи. Для этого к обычному минимизируемому функционалу прибавляется так называемый "стягивающий потенциал", исчезающи по мере приближения расстояния между концами цепи к эталонному значению.
3. Метод Шераги
Авторам [4] удалось включить в набор независимых структурных параметров все N межъядерных расстояний и N валентных углов. Теперь лишь N-6 углов внутреннего вращения требуется задавать во входных данных. Оставшиеся шесть зависимых торсионных углов должны удовлетворять системе из шести уравнений, формулирующих условия замыкания цикла, сводящейся к уравнению с весьма громоздкими коэффициентами, решаемому итерационно.
4. Метод Нордландера [5]
Строится линейная цепь из N-1 атома. Если расстояние между концами этой цепи не превышают суммы длин двух оставшихся связей, то замыкание легко обеспечивается достраиванием последнего атома между этими концами. Метод формально неитерационный, но обеспечить отмеченное требование к стартовому набору структурных параметров практически невозможно без итерационного подбора.
Набор независимых параметров содержит N межъядерных расстояний, N-2 валентных угла и N-4 угла внутреннего вращения.
5. Метод построения пространственных моделей циклических молекул
Недостатки предыдущего метода в конечном итоге вытекают из неудачного выбора замыкающего (одноатомного) фрагмента, предопределяющего жесткие требования к расстоянию между концами основной цепи. В предлагаемом методе роль замыкающего фрагмента играет цепочка, равная примерно половине длины строящегося цикла. Значительно больший диапазон возможных значений расстояний между ее концами, с учетом сопоставимости длин обеих цепочек, обеспечивает построение цикла практически при любых разумных вариациях стартового набора структурных параметров с помощью следующей схемы:
1. Разбиваем цикл на две примерно одинаковые по длине цепи (основную и рабочую), состоящие из M и L атомов соответственно (M + L = N + 2). Строим обе цепочки с помощью одного из алгоритмов построения нециклических молекул [2], обеспечивая их ориентацию относительно оси OX в соответствии с рис. 1а. б.
2. Вычисляем расстояния (R1 и R2) между концами цепей.
3. Поворотом правой ветви рабочей цепи вокруг оси OX на угол добиваемся, чтобы расстояния между концами цепей совпали. Это возможно при двух значениях угла (1 и 2):
1 = Arcsin(C/) - Arcsin(B/),
2 = - Arcsin(C/) - Arcsin(B/),
где = Sign(A) * sqrt(A2 + B2)
A = y1 * zm - z1 * ym
B = y1 * ym + z1 * zm
C = (R22 - R21) / 2 + B.
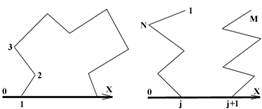
Рис. 1. Ориентация основной (а) и рабочей (б) цепей.
Знак параметра A совпадает со знаком вспомогательного торсионного угла F1,J,J+1,M . В случае, если в исходной цепи четыре атома 1,J,J+1,M попадают в плоскость (то есть F = 0,p), параметр A обращается в ноль. При этом y1 = -y2. Однако при смене знака параметра A решения скачком меняются местами. При этом малые изменения структурных параметров приведут к большим изменениям геометрии молекулы, в частности, возможен самопроизвольный переход от одного оптического размера к другому. Анализ показывает, что избежать зависимости результата от выбора стартового приближения и обеспечить непрерывное изменение геометрии можно, если выбирать окончательное решение следующим образом:
| f = | { | y1, если sgn1 * Sign(A) > 0 y2, если sgn1 * Sign(A) < 0 |
Параметр sgn1 введен для управлением выбором нужного решения. Значение sgn1 = 1 приводит к конформации цикла, наиболее близкой к стартовой в том смысле, что вспомогательный торсионный угол F при построении цикла не будет менять знак. Значение sgn1 = -1 изменит знак F и приведет к конформеру, отвечающему тому же набору независимых параметров, но с другими значениями зависимых параметров.
В случае abs(C/r) > 1 построение цикла с заданным набором параметров невозможно, поскольку значение R1 не попадает в интервал [Rmin , Rmax] изменения расстояния R2. Для корректировки вводимых значений структурных параметров полезно иметь в виду, что если C < 0, то R1 > Rmax, а если C > 0, то R1 < Rmin.
4. Цепочки соединяются концами (рис. 2).
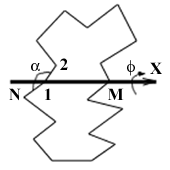
Рис. 2. Замыкание цикла.
5. Цикл перегибается по линии соединения до придания независимому валентному углу a 21N заданного значения. Соответствующий угол f 21MN может быть вычислен по формулам пункта (3), если в качестве параметров R1 и R2 взять легко вычисляемое конечное и исходное значения межъядерного расстояния R2,N. При этом также возникает два варианта решения, для выбора из которых необходимо ввести второй знаковый параметр sgn2. Если заданный угол a несовместим с условием замыкания цикла (при этом abs(C/r) > 1), то его следует увеличить, если C > 0, или уменьшить, если C < 0.
Пошаговый перебор значений независимых торсионных углов для всех четырех комбинаций знаковых параметров sgn1 и sgn2 позволит получить полный набор конформеров исследуемой циклической системы.
Отметим также, что, в отличие от предыдущего метода, содержащего два зависимых валентных угла, предлагаемый алгоритм использует лишь один зависимый валентный угол M-1,M,M+1. Следовательно, в наборе независимых параметров содержится на один труднооцениваемый торсионный угол меньше. Это уменьшает на единицу размерность пространства перебора структур и значительно ускоряет конформационный поиск.
Предлагаемый алгоритм формально применим к карбо- и гетероциклам, начиная с пятичленного, однако его достоинства (быстродействие и работоспособность в относительно широком диапазоне заданных значений независимых параметров) в наибольшей степени проявляются для макроциклических систем.
Список литературы
Mastryukov V.S., Simonsen S.H. Empirical correlations in structural chemistry // Molecular Structure Research 1996. V.2. P.163-189.
Атавин Е.Г., Тихоненко В.О. Построение 3D-моделей нециклических молекул в естественных переменных // Вестник Омского университета. 1998. №2. С.35-37.
Дашевский В.Г. Конформационный анализ органических молекул. М.: Химия, 1982.
Go N., Scheraga H.A. Ring closure and local conformational deformation of chain molecules. Macromolecules. Vol.3. N2. P.178-187. 1969.
Nordlander J.E., Bond A.F., Bader M. Atcoor: a program for calculation and utilization of molecular atomic coordinates from bond parameters // Computers & Chemistry. 1985. V.3. P.209-235.
Для подготовки данной работы были использованы материалы с сайта http://www.omsu.omskreg.ru/
Похожие работы
... мере, синергетическим стилем мышления может быть некой платформой для открытого творческого диалога между учеными, мыслителями, деятелями искусства, имеющими различные творческие установки и взгляды на мир. 2. Некоторые парадоксальные следствия синергетики Множество новых парадоксальных идей, образов и представлений возникает в синергетике. Кроме того, с точки зрения синергетики может быть ...
... могут быть данные различных типов (целые или вещественные числа, строки, логические значения). Соответственно переменные бывают различных типов: целочисленные (А%=5), вещественные (А=3.14), строковые (А$="информатика'1), логические (A=True). Массивы являются набором однотипных переменных, объединенных одним именем. Массивы бывают одномерные, которые можно представить как одномерные ...
... и в тех, когда физическое качество переходит в химическое, химическое в биологическое, биологическое в надбиологическое, профанное в сакральное и наоборот, - мы неизменно имеем дело с синергетикой, с феноменологией сопряжении и метаморфоз, с ситуацией взаимопревращений противоположностей, с теми неаддитивно-мета-системными переходами, которые в конкретно-образной (мифологической, поэтической) или ...
... , ведении войны, обороне и т.д. Таким образом, культура - это класс символизированных предметов и явлений, рассматриваемых в экстрасоматическом контексте. До появления культурологии в процессе расширения сферы наукиi натуралистическое (т.е. немифологическое, нетеологическое) объяснение поведения людей носило биологический, психологический или социологический характер. Соответственно то или иное ...
0 комментариев