Условие на оси симметрии

3.4 Условие на оси симметрии

(9)

Задача, сформулированная в выражениях (1-9) есть краевая задача, которая решается численным методом.

Аппроксимировав на сетке методом конечных разностей (МКР), получим дискретное сеточное решение.

T_i=f(x_i;t^k).

Метод расчета

Будем использовать МКР – метод конечных разностей.

Сформулированную краевую задачу дискретизируем на сетке.

= - шаг по пространству постоянный; - шаг по времени переменный

Для аппроксимации задачи на выбранной сетке можно использовать разные методы – шаблоны. Наиболее известные из них для данного типа задач четырех точечный конечно разностный шаблон явный и неявный.

Явный четырех точечный шаблон Неявный четырех точечный шаблон

Использование явного шаблона для каждого временного шага получаем n+1 уравнение с n неизвестными и система решается методом Гауса, но сходимость решения только при очень малых шагах.

Использование неявного шаблона обеспечивает абсолютную сходимость, но каждое из уравнений имеет 3 неизвестных, обычным методом их решить невозможно.

По явному:

(10)

По неявному:

(11)

Сходимость обеспечивается при:

при явном шаблоне (12)

-точность аппроксимации

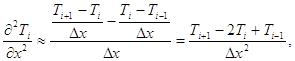(13)

Схема апроксимации

Аппроксимируем задачу 1-9 на четырех точечном неявном шаблоне

Начальные условия:

(14)

(15)

(16)

(17)

(18)

Граничные условия:

(19)

(20)

(21 a)

=> (21)

Условие идеального контакта на границе отливка форма

(22)

Расчет временного шага :

Величина -var рассчитывается из условия, что за промежуток времени  фронт перейдет из точки nf в точку nf+1

Расчет ведут итерационными (пошаговыми) методами

Строим процедуру расчета следующим образом:

Вычисляем нулевое приближенное для каждого шага,

За шаг итерации примем S,

Нулевое приближение S=0.

(23)

Уточняем шаг: S+1

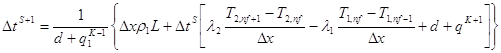(24)

d – параметр итерации от 0 до 1

для расчета возьмем d=0.

Число S итераций определяется заданной точностью:

Временного шага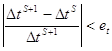 (25)

И по температуре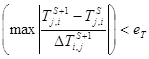 (26)

e_t и e_T – заданные точности по времени и температуре

e_t=0,01c, e_T=0,1°C

Dt^I=0,01c – время за которое образовалась корочка.

Описанный итерационный процесс называют ''Ловлей фазового фронта в узел''.

Можно задать Dх, Dt^K=const, тогда неизвестно будет положение фронта, при помощи линейной интерполяции.

Расчет температурных полей:

Метод «прогонки»:

Считается наиболее эффективным для неявно заданных конечно-разностных задач.

Суть метода:

Запишем в общем виде неявно заданное конечноразностное уравнение второго порядка (14) в общем виде:

A_iT_i-1 – B_iT_i + C_iT_i+1 + D_i = 0 ; i = 2, 3, 4, …n-1 (27)

действительно для всех j и k.

и краевые условия для него:

T₁ = p₂T₂ + q₂ (28 а)

T_n = p_nT_m-1 + q_n (28 б)

T_i = f(A_i; X_i; t_k) - сеточное решение.

A_i, B_i, C_i, D_i – известные коэффициенты, определенные их условий однозначности и дискретизации задачи.

Решение уравнения (27) – ищем в том же виде, в котором задано краевое условие (28 а)

T_i = а_i+1T_i+1 + b_i+1 ; i = 2, 3, 4, …n-1(29)

A_i+1, b_i+1 – пока не определенные «прогоночные» коэффициенты (или коэффициенты разностной факторизации)

Запишем уравнение (29) с шагом назад:

T_i-1 = а_iT_i + b_i (30)

Подставим уравнение (30) в уравнение (27):

A_i(a_iT_i + b_i) – B_iT_i + C_iT_i+1 + D_i = 0

Решение нужно получить в виде (29):

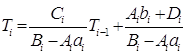(31)

Найдем метод расчета прогоночных коэффициентов.

Сравним уравнение (29) и (31):

(32)

(33)

(32),(33)– рекуррентные прогоночные отношения позволяющие вычислить прогоночные коэффициенты точке (i+1) если известны их значения в точке i.

Процедура определения коэффициентов а_i+1 и b_i+1 называется прямой прогонкой или прогонкой вперед.

Зная коэффициенты конечных точек и температуру в конечной точке Т_i+1 можно вычислить все Т_i.

Процедура расчета температур называется обратной прогонкой. То есть, чтобы вычислить все Т поля для любого t_k нужно вычислить процедуры прямой и обратной прогонки.

Чтобы определить начальные а₂и b₂, сравним уравнение (29) и уравнение (28 а):

a₂ = p₂; b₂ = q₂

Запишем уравнение 29 с шагом назад:

T_n = p_nT_n-1 + q_n

T_n-1 = q_nT_n + b_n

(34)

Новая задача определить p_n , q_n

Вывод расчетных формул:

Преобразуем конечноразностное уравнение (14) в виде (27)

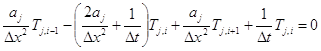, j=1,2 (35)

относиться к моменту времени k

Из (35) => A_i=C_i= B_i=2A_i+ D_i= (36)

Определим значения коэффициентов для граничных условий:

на границе раздела отливка-форма

(37)

приведем это выражение к виду (28 а)

 отсюда (38)

b₂=q₂= a₂=p₂=1 (39)

на границе раздела Me_тв - Ме_ж

из (29), T_nf=T_n=> a_nf+1=0, b_nf+1=T_s (40)

условие на оси симметрии

T_n-1=T_nв соответствии с (21)

p_n=1, q_n=0 (41)

подставив (41) в (34) получим

(42)

Алгоритм расчета

1)   Определить теплофизические характеристики сред, участвующих в тепловом взаимодействии λ₁, λ₂, ρ₁, ρ₂, L, а₁, а₂, Т_s, Т_н, Т_ф.

2)   Определить размеры отливки, параметры дискретизации и точность расчета

2l₀=30 мм, l₀=R=15 мм=0,015 м

n=100,

первый шаг по времени: Δt¹=0,01 с, t=t+Δt

е_t=0,01 с, e_t=0,1 ^оC

3)   Принять, что на первом временном шаге к=1, t₁=Δt¹, nf=1, Т₁=Т₃, Т_i=Т_н, , i=2,…,n, Т₄=Т_ф

4)   Величина плотности теплового потока на границе раздела отливка – форма

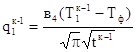(43)

, s=0, (нулевое приближение)

к=2, (44)

5)   Найти нулевое приближение Δt^{к, 0} на к-том шаге

переход nf → i → i+1 по формуле (23)

6)   Найти коэффициенты A_i, С_i, В_i, D_i по соответствующим формулам для сред Ме_тв. и Ме_ж. В нулевом приближении при s=0

7)   Рассчитать прогоночные коэффициенты a_i+1, b_i+1 для Ме_тв. и Ме_ж., s=0 с учетом что Т_nf=Т_з.

Т₁=р₂Т₂+g₂

Т_i=а₂Т₂+в₂

Найти а₂ и в₂:

а₂=1, (45)

(46)

8)   Рассчитать температуру на оси симметрии

(47)

9)   Рассчитать температурное поле жидкого и твердого металла

(48)

10)    Пересчитать значения ∆t_к по итерационному процессу (24)

d – параметр итерации (d=0…1)

проверяем точность;

11)    Скорость охлаждения в каждом узле i рассчитать по формуле:

, ^оС/с (50)

12)    Скорость затвердевания на каждом временном шаге:

, м/с (51)

13)    Средняя скорость охлаждения на оси отливки:

14)    Положение фронта затвердевания по отношению к поверхности отливки

, к – шаг по времени (52)

15)    Полное время затвердевания

, к′ - последний шаг (53)

16)    Средняя скорость затвердевания отливки

(54)

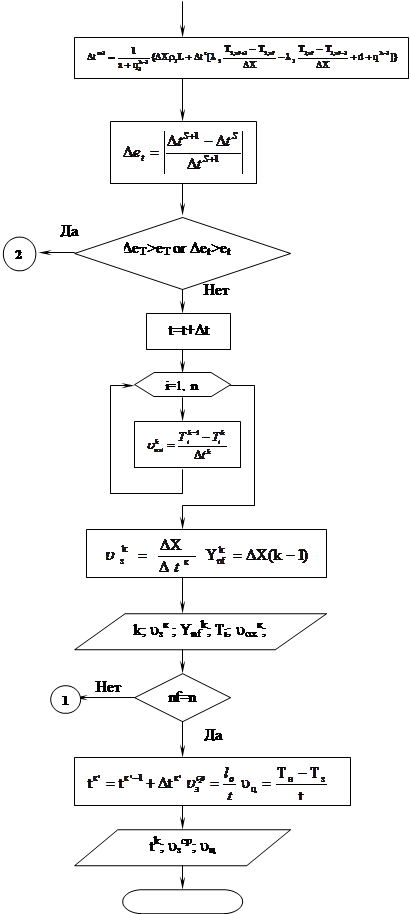
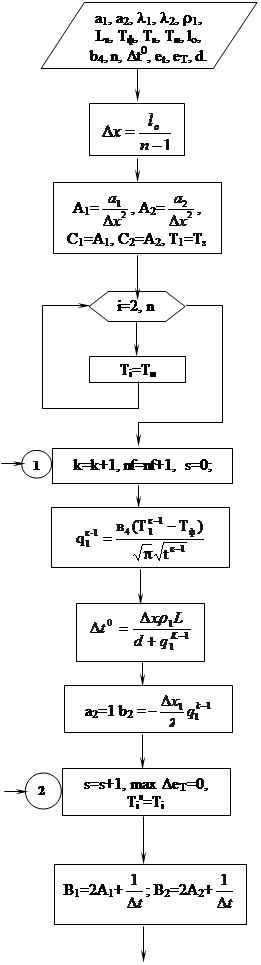Идентификаторы Блок-схема

- [Вводим исходные данные

- [Вычисляем шаг по пространству

- [Вычисляем коэффициенты А_j, С_j для подстановки в (32), (33) и задаем температуру в первой точке

- [Температурное поле для первого шага по времени

- [Делаем шаг по времени

- [Вычисляем плотность теплового потока

- [Шаг по времени в нулевом приближении

- [Начальные прогоночные коэффициенты

- [Шаг по итерации

- [Вычисляем коэффициенты B_j для подстановки в (32), (33)

- [Вычисляем прогоночные коэффициенты по твердому металлу

- [Прогоночные коэффициенты для фронта

- [Вычисляем прогоночные коэффициенты по жидкому металлу

- [Температура на оси симметрии

- [Расчет температурного поля

- [Ищем максимальный температурный шаг

- [Уточняем Dt

- [Точность временного шага

- [Проверка точности

- [Расчет времени

- [Скорость охлаждения в каждом узле

- [Скорость затвердевания и положение фронта

- [Вывод результатов

- [Проверка достижения фронтом центра отливки

- [Расчет полного времени, ср. скорости затвердевания ср. скорости охлаждения на оси отливки

Вывод результатов

- [Конец.

Программа

CLEAR , , 2000

DIM T(1000), T1(1000), AP(1000), BP(1000), Vox(1000), N$(50)

2 CLS

N = 100: KV = 50: N9 = 5: L = .015

TM = 293: TI = 1345: TS = 1312.5

BM = 1300: a1 = .000036: a2 = .000021

TA0 = .01: ETA = .01: E = .01

l1 = 195: l2 = 101

R0 = 8600: LS = 221000

AF = 0: Pi = 3.14159265359#