Навигация
Колесо изображено на рисунке 2.6
1. Колесо изображено на рисунке 2.6.
Описание колеса в статике:
Упомянутым в патенте изобретением снабдили колесо, состоящее из круглого остова или обода, соединённого множеством пружин с центральной ступицей. Круглый обод лежит в плоскости вращения, ось которой преимущественно перпендикулярна данной плоскости и проходит через середину плоскости вращения, образуемой ободом. Более того, механизм колеса включает в себя дугообразные элементы пружин, которые расходятся лучами по спирали в радиальном направлении от ступицы до обода и обеспечивают наружную жесткость обода колеса с целью повышения эластичности и добавления большей ударопрочности.
Также в конструкции колеса предусмотрены два набора спиралевидных пружин, по одному с каждой стороны от плоскости вращения, передвигающихся, в основном, конически от каждой из сторон ступицы до обода колеса.
Еще в реализованном изобретении каждая из пружин в каждом из наборов имеет сопряженную пружину в другом наборе так, что первая пара сопрягается со второй парой в точке расхождения по длине до точки прикрепления к ступице.
Далее конструкция отличается тем, что спиральные элементы в одном блоке не выровнены относительно друг друга, соседа или оппозитного элемента, так чтобы не организовать заранее отобранные шаблоны.
Спиральные элементы в одной группе растягиваются по спирали по часовой стрелке от центра к периферии, тогда как пружины другой группы растягиваются против часовой стрелки, если смотреть на колесо сбоку от плоскости вращения.

 Также в конструкции ось колеса разъединена между ступицами, т.е. колесо закреплено двумя вставками, соединяющими с обеих сторон вилку и ступицу. Промежуток между ступицами остаётся, то есть отсутствует соединение между оппозитными ступицами.
Также в конструкции ось колеса разъединена между ступицами, т.е. колесо закреплено двумя вставками, соединяющими с обеих сторон вилку и ступицу. Промежуток между ступицами остаётся, то есть отсутствует соединение между оппозитными ступицами.
Выбор специфической конфигурации или модели двойных спиралевидных деталей в изобретенном колесном устройстве позволяет, по крайней мере, добиться искомого распределения усилий или достичь требуемой в ряде задач поворачиваемости и сцепления. Таким образом, горные велосипедные шины могут нуждаться в соприкосновении обоих сторон спиралевидных элементов для передачи наибольшей гибкости и улучшенной упругости, поскольку в значительной степени идентичность или согласованность блоков спиральных шестерен может придать большую поворачиваемость единичному колесу лопастного типа роликовых коньков, т.е. так называемым роликовым лезвиям.
2. Цель изобретения. Данный патент США можно считать логическим завершением целой цепочки изобретений (патенты США №№ 813423, 1141078, 515456, 2869608, 1253975), постепенно развивающих и улучшающих данный конструкционный узел машины путем введения и модернизации связей различного типа в колесе с внутренним подрессориванием. Например, патент США №813423 Хилла показывает когтеобразное удерживающее устройство для прикрепления колеса к оси. Конструкция Хилла включает в себя прочные спицы из металлической проволоки, которые соединяют каждую ступицу с ободом колеса, что распределяет усилия так же, как и ось, располагающаяся, как правило, между этими ступицами. Патент США №1141078 Шеффела улучшает конструкцию Хилла путём исключения удерживающих устройств, крепящих ступицу к оси. Шеффел также предлагает ввести прочные спицы из проволоки и единый вал колеса. Патент США №515456 Вуда направлен, в основном, на конструкцию ступицы колеса, и показывает дугообразные спицы, лежащие вне плоскости вращения колеса, и перемещающиеся по дуге от ступицы к ободу колеса. Патент США №2869608 Чамберлена и др. защищает конструкцию пружинного колеса под автомобильные шины, имеющую плоские ленточные пружины (вместо спиц), которые внутренне расходятся от каждой ступицы до обода колеса, при этом полностью находясь вне плоскости вращения обода. Наконец, патент США №1253975 Ховарда и др. защищает конструкцию с множеством некомпланарных спиц, прикрепленных к множеству независимых ободов. Данный же патент США №5125443, в свою очередь, содержит колесо открытого типа, имеющее круглый обод, расположенный в плоскости вращения колеса, две оппозитные ступицы, размещённые по обе стороны плоскости вращения колеса на его оси вращения, саму ось, пересекающую плоскость вращения в центре круга, очерченного ободом, и множественные пружины, расположенные противоположно друг другу, причем каждая из этих пружин расходится от центра к периферии по радиальной и спиралевидной траектории от точек прикрепления к ободу до точек прикрепления к ступицам, в связи с чем колесо наделяется способностью лучше противостоять радиальным и/или боковым деформациям, обеспечивая притом хорошую самоцентровку и возврат в начальное положение, когда обод колеса перемещается из нормального положения в плоскости вращения или по оси вращения.
2.2.5 Достоинства и недостатки рассмотренных конструкцийВсе вышеописанные изобретения обладают рядом недостатков, не позволяющих применить эти колёса как ведущие на гусеничных тракторах.
Первый недостаток всех изобретений — они проектировались не для гусеничных тракторов, следовательно, абсолютно не учитывают специфику работы данного тапа машин. Более того, каждое из приведенных выше изобретений, несмотря на оригинальные идеи, не подходят конструктору гусеничных машин по ряду причин. Так у первого изобретения значительная металлоёмкость и небольшая величина хода обода, что значительно снижает плавность хода и удорожает конструкцию. То же можно сказать и о третьем из списка изобретении, которое идеально подходит для применения в опорных катках гусеничного движителя. Второе из описанных изобретений имеет и малую металлоемкость, и хорошую плавность хода, но всё же оно недостаточно удовлетворяет требованием жесткости в боковом направлении для данного типа ведущих колес. Последний из описанных патентов и авторских свидетельств хотя и обладает достаточно малой металлоемкостью и хорошей плавностью хода, что не маловажно, тем не менее, не содержит возможность обратимости движения (за исключением последней из предложенных конструкций), имеет большую степень детализации, что снижает его эксплуатационные качества, а главное, идеология данного изобретения подразумевает наличие гибкого обода колеса, что недопустимо в гусеничных движителях из-за необходимости обеспечивания адекватного натяжения гусеницы и обеспечения её несоскальзывания.
Несмотря на все описанные выше недостатки, большинство оригинальных идей, примененных в данных изобретениях требуют отдельного более пристального изучения при синтезе новой конструкции опущенного на грунт ведущего колеса с внутренним подрессориванием гусеничного трактора.
3. Анализ работы объекта исследования 3.1 Требования, предъявляемые к конструкции
Ведущее колесо наматывает гусеничную цепь, обеспечивая движение трактора. К ведущему колесу предъявляются следующие требования:
— надежное зацепление с гусеницей (независимо от её износа) как в ведущем, так и в тормозном режиме. Это требование соблюдается путем правильного выбора геометрии зацепления. Оно легко выполняется в гусеницах, шаг которых в процессе эксплуатации не изменяется или изменяется незначительно [8];
— высокая износостойкость зубьев. Обеспечивается геометрией зацепления, подбором износостойких материалов для зубчатых венцов и технологическими мероприятиями по повышению их поверхностной твёрдости;
— самоочистка от пыли, грязи и снега.
В данной работе рассматривается возможность создания на базе гусеничного трактора (прототип — трактор ВТ–100, выпускаемый ВГТЗ) варианта сельскохозяйственного трактора общего назначения с подрессоренным ведущим колесом.
Ведущее колесо опускается на землю, тем самым оно выполняет две роли: ведущую и опорную [15, 16].
Опуская ведущее колесо на грунт, получаем следующие преимущества:
— увеличение КПД;
— уменьшение удельного давления на почву;
— уменьшение буксования;
— увеличение опорной длины гусеницы;
— почвосбережение.
Однако простое увеличение продольной базы трактора путём опускания ведущего колеса на грунт ведёт к увеличению момента сопротивления повороту. А самое главное, на ведущее колесо теперь будут действовать ничем не компенсируемые силы, которые приведут к выходу из строя конечной передачи. Поэтому ведущее колесо необходимо подрессоривать.
3.2 Описание конструкции и принципа работы ведущего колеса с внутренним подрессориваниемПредложенное в данной работе ведущее колесо состоит из (см. рисунок 3.1):
1. вала конечной передачи;
2. ведущей ступицы;
3. нескольких ведомых ступиц;
4. зубчатого венца;
5. системы подрессоривания;
6. дополнительной системы подрессоривания;
7. втулок-упоров.

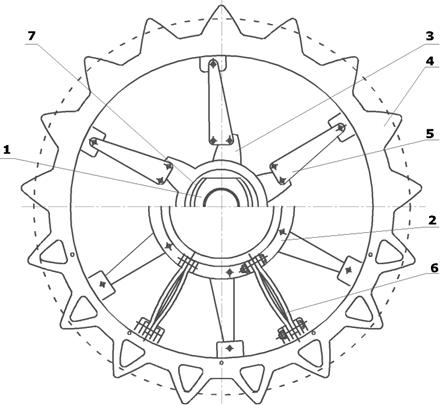
Предлагаемая к защите конструкция системы подрессоривания состоит из четного количества упругих элементов треугольной формы 5 расположенными между ведущей 2 и ведомыми 3 ступицами колеса с одной стороны и зубчатым венцом 4 — с другой. Упругие элементы верхним концом шарнирно закреплены на зубчатом венце. Снизу они также шарнирно крепятся на ведущей ступице и попарно закрепляются с возможность совершать вращательное движение в плоскости колеса на ведомых ступицах. Следовательно, количество ведомых ступиц 4 равно числу упругих элементов, размещенных на колесе, делённое на два.
 |
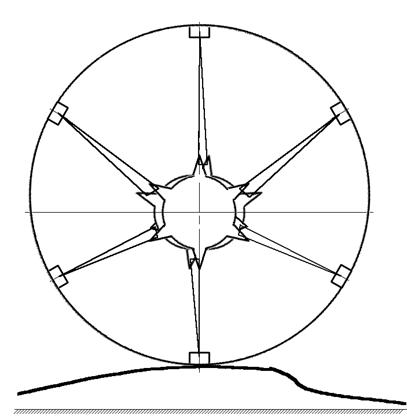
Упругие элементы 6 числом равные числу упругих элементов 5 и расположенные в плоскости, параллельной оси вращения колеса, установлены для компенсирования действия сил боковой нагрузки Данные элементы могут быть заменены защитным кожухом, напрямую соединяющем ведущую ступицу 2 с зубчатым ободом 4, и также выполняющему роль компенсатора боковых возмущений.
Колесо работает следующим образом (рисунок 3.2).
Крутящий момент независимо от направления движения передаётся от ведущего вала конечной передачи 1 через ведущую ступицу 2 на упругий элемент 5, и через него на зубчатый венец 4 и, вследствие взаимодействия последнего с гусеницей и почвой, реализуется в тяговое усилие колеса. Передача крутящего момента осуществляется за счет того, что за счёт того, что с одной ведомой ступицей 3 связаны два упругих элемента, расположенных противоположно друг другу относительно оси ведущего колеса, которые создают усилие направленные в центр колеса, благодаря чему ведомая ступица 3 остаётся неподвижной и каждый из упругих элементов 5 работает как жесткая спица. При наезде на неровность (см. рисунок 3.2) зубчатый обод перемещается вверх, упругий элемент 5 проворачивается вокруг оси шарнира нижней опоры с ведущей ступицей 2 и вокруг оси шарнира верхней опоры с зубчатым ободом 4. Ведомая ступица при этом совершает плоско-параллельное перемещение по направляющим упора-втулки 7 в плоскости, перпендикулярной продольной оси вала, чем и обеспечивается свободный ход зубчатого обода. Подрессоривание при этом реализуется за счёт упругой деформации элементов 5 в плоскости, параллельной продольной оси вала. Деформация каждого из выше обозначенных элементов тем больше, чем ближе элемент к вертикальному положению, то есть своего максимального значения достигает в момент, когда шарниры крепления упругого элемента к зубчатому ободу и ведущей ступице расположены на одной линии, строго перпендикулярной поверхности качения. Исходя из вышесказанного следует, что динамические возмущения воспринимают все упругие элементы 5 конструкции, а в случае «открытого» исполнения к ним также присоединяются и упругие элементы 6. Гашение колебаний осуществляется за счет сил трения в шарнирах креплений упругих элементов 5 к другим деталям конструкции, сил трения между ведомыми ступицами 3 и упором-втулкой 7, а также за счет сил упругости, возникающих в элементах 5.
Стабилизацию колеса в поперечном направлении осуществляют упругие элементы 6 («открытая» компоновка) или защитная крышка-кожух.
3.3 Кинематический расчет исследуемой конструкцииВ данной части работы исследуется возможность работы предложенной конструкции с точки зрения её геометрической осуществимости. Необходимо определить размеры и месторасположение каждого из элементов колеса и сделать анализ их взаимодействия.
3.3.1 Определение точек кривой траектории движения конца упругого элемента
|
![]()
где а — перемещение ведомой ступицы;
R — радиус ведомой ступицы.


Далее также по теореме косинусов определим из треугольника ACD углы a1 и a2
|
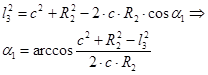
|
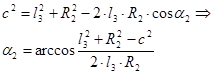
где l3 — сторона упругого элемента, соединяющая ведущую и ведомую ступицы.
По теореме синусов из треугольника АВС найдём углы s1, s2и a3:
|
|
|
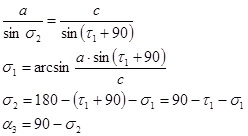
Из треугольника DME также по теореме синусов найдем е2 — высоту треугольника ADE, опущенную из точки Е и угол g2:
|
|
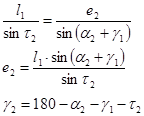
Далее из треугольника CFK находим e1 и а1 (см. рисунок. 3.3):
|
|
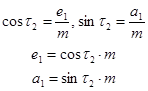
|
|
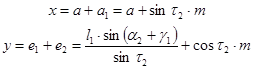
Данные результаты расчетов служат основой для компьютерного моделирования работы упругого колеса при движении по пересечённой местности.
3.3.2 Определение радиуса ведущего колеса по трём точкамВ связи с внесением изменений в конструкцию ведущего колеса, изменяется также и его радиус. Определить радиус колеса возможно методом «трёх точек», суть которого заключается в существовании и единственности окружности, проходящей через три точки с известными координатами, так называемыми «координатными точками».
Определим размеры отрезков а1, а2, а3 — хорд между координатными точками:
|
|
|
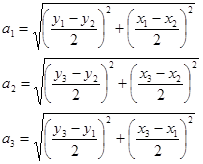
Из треугольника 123 (см. рисунок 3.4) найдём углы a1 и a2:
|
|
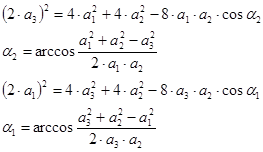
|
![]()
![]()
|
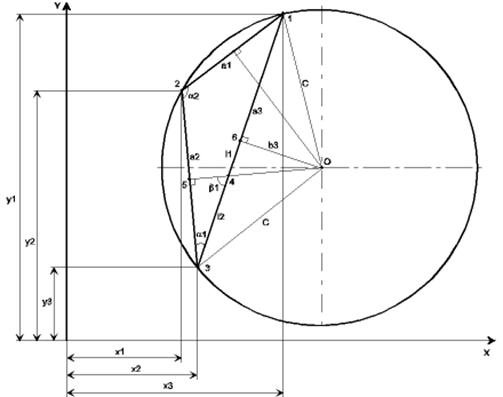
Из треугольников О46 и О63 найдём l2 — один из катетов треугольника О46
|
Далее из треугольника О46 находится второй катет b3:
|
![]()
Из треугольника О36 находим радиус с (см. рисунок 3.4):
|
что, с учетом выражений (3.1–3.3) запишется как
|
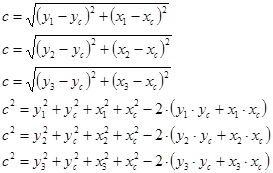
Основываясь на полученных выше соотношениях, определим координату центра по оси ординат:
|
|
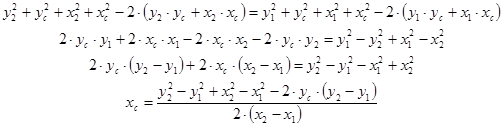
|
|
|
![]()
|
![]()
Проведём дальнейшие преобразования с целью определения координаты центра ведущего колеса по оси абсцисс.
|
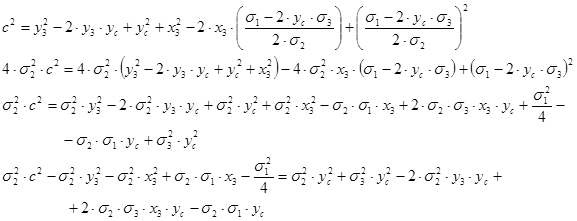
|
|
|
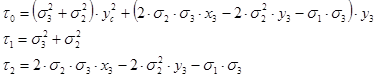
|
![]() ,
,
откуда:
|
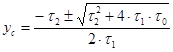
Избыточный корень отсекается по условию физической осуществимости.
Аналогичным образом поступим при определении координаты центра ведущего колеса по оси абсцисс:
|
|
|
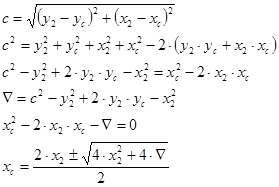 3.3.3 Определение координат шарниров упругих элементов колеса в любой момент времени
3.3.3 Определение координат шарниров упругих элементов колеса в любой момент времени Для построения модели работы ведущего колеса с внутренним подрессориванием необходимо определить, какое положение в каждый момент времени занимает каждый из упругих элементов системы подрессоривания. колеса. Первым шагом на пути решения этой задачи является определение координат точек шарниров упругих элементов.
Исходные данные:
—
|
![]()
— максимальное смещение зубчатого обода относительно оси вращения колеса:
|
— закон изменения угла поворота колеса:
|
—
|
![]() ,
,
|
— радиус ведущей ступицы:
|
—
|
![]() .
.
|
|
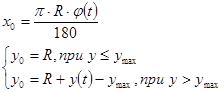 .
. Тогда координаты точки шарнира К, принадлежащей ведущей ступице определятся, как
|
Теперь можно определить координаты точки шарнира L, принадлежащей зубчатому ободу колеса:
|
По известным координатам двух точек шарнира и размерам прямоугольного треугольника, чью форму имеет упругий элемент, вычисляем координаты точки шарнира К, физически принадлежащей ведомой ступице. Для этого определим расстояние а между точками М и L (см. рисунок 3.5):
|

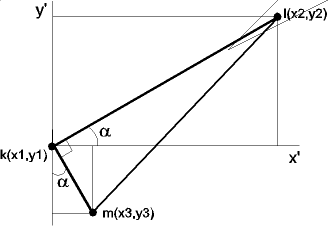
Далее определим величину угла a, угла между прямой KL и осью ОХ’ и равному ему, как углу со взаимно перпендикулярными сторонами, углу между прямой KM и осью OY’:
|
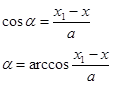
Отсюда координаты точки шарнира М найдутся как:
|
Расчет данных параметров при помощи вычислительной техники позволит точно закоординировать положение любого из элементов ведущего колеса в процессе движения. Использование результатов данных расчетов делает возможной реализацию программного симулятора движения упругого колеса по неровной поверхности при помощи одноимённого пакета прикладного моделирования работы механизмов американской фирмы AEngiCAD.
4. Физическая осуществимость кинематической модели ведущего колеса с внутренним подрессориванием 4.1 Кинетостатический анализ работы ведущего колеса с внутренним подрессориванием. 4.1.1 Расчетная схема
Расчетная схема для кинетостатического анализа приведена на рисунке 4.1.

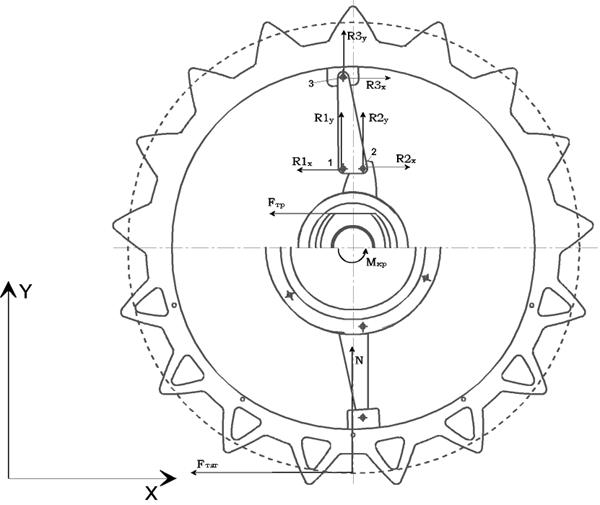
Принятые допущения:
— все тела абсолютно жесткие;
— на обод воздействует только нижняя ветвь гусеницы с силой Fтр;
— крутящий момент передаётся к любой точке обода колеса без потерь;
— упругий элемент в данный момент времени не деформирован, то есть с его стороны на обод, ведущую и ведомые ступицы не действуют силы упругости;
— центр вращения колеса, шарниры 1 и 3 всегда лежат на одной прямой;
— сила трения линейно зависит от реакции опорной поверхности;
— модуль реакции опорной поверхности равен силе тяжести машины, приходящейся на данный узел.
4.1.2 Определение неизвестных реакций в шарнирах упругого элементаЗапишем уравнения кинетостатики для данной системы:
|

|
|
![]()
|
где х — расстояние от поверхности трения до шарнира 1 (определяется из конструкции механизма).
|
|
|
![]() .
.
Тогда выражения (4.1) примут вид
|
|
![]()
|
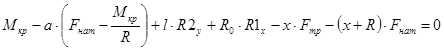
|
|
|
![]()
Данные зависимости выведены для крайнего вертикального положения колеса. Уравнения для определения реакций в общем случае не приводятся в данной работе ввиду их громоздкости.
Таким образом, подставляя в полученные соотношения данные, полученные при конструкторском анализе механизма, и передавая полученные данные в программу, работающую на компьютере, становится возможным получить статистику распределения реакций в шарнирах за один цикл, равный одному обороту колеса.
4.2 Расчет на изгиб пластинчатых упругих элементов, расположенных в плоскости, перпендикулярной оси ступицыВопрос расчета упругих элементов треугольной формы выходит далеко за рамки обычного курса сопротивления материалов и не решается стандартными методами. Безусловно, данная задача имеет приоритет в дальнейших исследованиях. Однако, повторюсь, это отдельный вопрос, требующий внимательного изучения с точки зрения теории упругости.
В данной работе производится оценочные расчеты в первом приближении, позволяющие сделать вывод о физической реализуемости предлагаемой конструкции.
Предположим, что пластинчатый упругий элемент имеет форму прямолинейного центрально сжатого стержня.
Данный стержень при определённой величине нагрузки может оказаться в опасном (критическом) состоянии безразличного равновесия. При этом прямолинейная форма оси стержня будет неустойчива, и стержень может «выпучиться». Нагрузка, при которой прямолинейная форма перестаёт быть формой устойчивого равновесия, называется критической. При критической нагрузке стержень переходит к новой, криволинейной форме равновесия, что связано с появлением качественно новых деформаций. Сжимающая сила вызывает дополнительные изгибающие моменты, линейная зависимость между нагрузками и деформациями нарушается; наблюдается сильное нарастание прогибов при малом увеличении сжимающей силы. Это явление называется продольным изгибом. Переход в критическое состояние, как правило, сопровождается потерей несущей способности стержня и называется потерей устойчивости. Для обеспечения устойчивости заданного деформированного состояния в конструкциях и сооружениях допускаются нагрузки, составляющие лишь часть критических. Отношение критической нагрузки к её допускаемой величине называется коэффициентом запаса устойчивости:
|
Коэффициент ny зависит от материала стержня (рессоры). Его рекомендуемые величины находятся в пределах: для стальных стоек — 1,5¸3; для деревянных — 2,5¸3,5; для чугунных —4,5¸5,5.
Допускаемая нагрузка при расчётах на устойчивость не должна превышать значения
|
Ниже приводится методика расчета для определения критических (эйлеровых) сил центрально сжатых стержней. Эти формулы справедливы лишь при статистических нагрузках, вызывающих сжимающее напряжение ниже предела пропорциональности материала стержня sп. Другими словами, применимость этих формул определяется условием:
|
где sкр — критическое напряжение;
F — площадь поперечного сечения;
Е — модуль продольной упругости материала;
![]() — приведенная гибкость стержня при продольном изгибе;
— приведенная гибкость стержня при продольном изгибе;
imin — наименьший радиус инерции поперечного сечения;
m — коэффициент приведённой длины;
l — длина стержня (рессоры).
В общем случае сжатого монолитного стержня (рессоры) критическая сила определяется как:
|
где Jmin — наименьший из главных центральных моментов инерции сечения
l — полная длина стержня;
 — коэффициент критической нагрузки.
— коэффициент критической нагрузки.
Коэффициенты h и m зависят от способа закрепления торцовых и промежуточных сечений рессоры, характера её нагружения продольными силами, закона изменения сечения стержня по длине.
Для рессор постоянного сечения, нагруженных продольными силами, приложенными к их торцевым сечениям, коэффициент h зависит только от условий закрепления концов рессоры. При сжатии рессоры с эксцентриситетом в пределах упругих деформаций наблюдается сложная нелинейная зависимость между напряжениями и сжимающей силой. Величина эксцентриситета е влияет на быстроту нарастания деформаций: чем больше эксцентриситет, те быстрее нарастают прогибы при увеличении сжимающей силы Р.
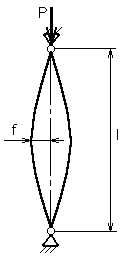
Рассмотрим рессору, шарнирно закреплённую на концах (см. рисунок 4.2).
Если сжимающие силы приложены на концах с эксцентриситетом е, прогиб посредине стержня приближенно равен:
|

Если сжимающая сила Р стремится к эйлеровой критической силе, ![]() , прогиб быстро возрастает. Если до загружения стержень (рессора) имела начальное искривление, которое приближенно можно считать синусоидой с одной полуволной и амплитудой f0, то при действии продольной силы Р дополнительный прогиб посредине будет равен:
, прогиб быстро возрастает. Если до загружения стержень (рессора) имела начальное искривление, которое приближенно можно считать синусоидой с одной полуволной и амплитудой f0, то при действии продольной силы Р дополнительный прогиб посредине будет равен:
|
В этом случае прогиб также неопределённо возрастает, если сжимающая сила приближается к критическому значению.
Исходя из сказанного выше, применительно к нашей задаче можно сказать, что критическая сила для конической консольной балки может быть вычислена по формуле (4.16) как
|
Дополнительный прогиб, связанный с начальным искривлением:
|
|
![]()
Напряжения в крайних сжатых волокнах стойки от сжимающей силы Р и изгибающего момента Ру будет, согласно [22]:
|
следовательно, прочность стойки обеспечена.
Данные для расчетов взяты из программы расчета реакций в шарнирах упругих элементов, входящей в пакет программ прикладного моделирования AEngiCAD.
5. Анализ результатов проведённых исследований 5.1 Программная эмуляция работы ведущего колеса с внутренним подрессориванием на поверхности с неровностями почвы
Как уже неоднократно упоминалось выше, результаты кинематического и кинетостатического анализа передаются в ПЭВМ с целью построения адекватной модели движение колеса по поверхности с неровностями почвы.
Данная программная эмуляция, преследуя определенные и описанные выше цели, в качестве объектов исследования использует ключевые точки колеса. В данном случае в их роли применяются координаты точек шарниров упругих элементов как необходимые и достаточные условия, однозначно определяющие положение каждого из элементов колеса в пространстве и времени. Более того, для каждой из указанных точек также измерялись величины реакций, размер деформации упругого элемента, величину крутящего момента. В силу громоздкости вычислений и невозможности проверки полученных данных на опытно-экспериментальной модели остановимся лишь на геометрическом моделировании работы.
Обратимся к рисункам 5.1–5.3. На них в виде графических примитивов, заменяющих элементы колеса, изображены стадии движения колеса при наезде на неровность. Рассмотрим их подробнее.
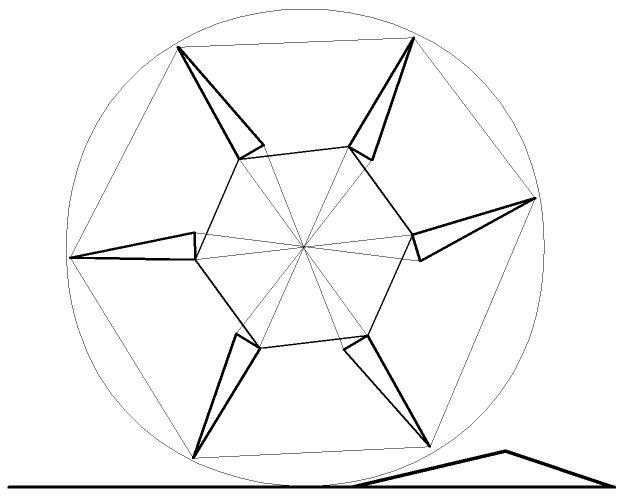

На рисунке 5.1 мы видим, что колесо занимает нейтральное положение, обод равноудален от ведомых ступиц, упругие элементы равнодеформируемы. В таком режиме колесо движется с наименьшими потерями крутящего момента (98%–100% от номинала), не вызывая каких либо перемещений в механизме подрессоривания.
Рисунок 5.2 показывает стадию наезда колеса на неровность почвы, когда высота неровности меньше вертикального хода обода, составляющего 70–90 мм, в зависимости от конструктивных параметров.

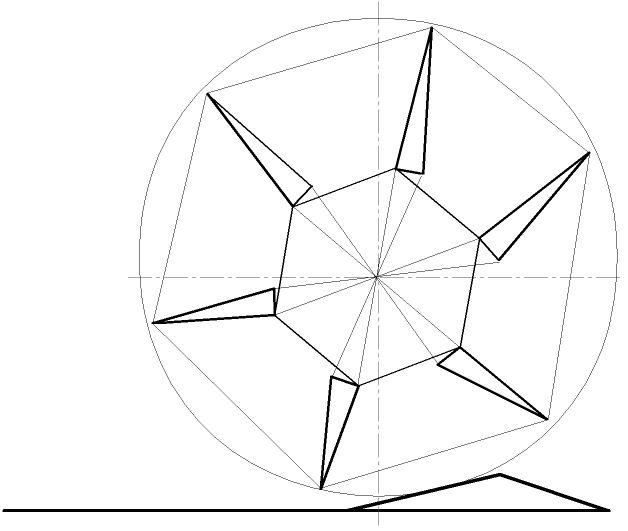

Зубчатый обод, замененный в программе на окружность соответствующих пропорций, перемещается по вертикали относительно центра вращения самого колеса, приводя в движение упругие элементы (треугольники) и ведомые ступицы (прямые линии). Упругие элементы претерпевают деформацию, расширяясь в верхней части колеса и сжимаясь в нижней. Колесо движется с небольшими потерями крутящего момента (92%–98% от номинала, по оценочным расчётам программы). Перемещения ведущих ступиц укладываются в расчетные. Реакции в шарнирах не превышают максимально предусмотренные.
И, наконец, на рисунке 5.3 показан момент максимального перемещения обода колеса, с максимальной упругой деформацией подрессоривающих элементов.


При этом ведомые ступицы максимально перемещаются вдоль направляющих, выбирая весь заложенный зазор, упругие элементы испытывают максимальную деформацию (до 3/5 от запаса прочности), крутящий момент падает до 88%–90% от номинала (однако, так как данный режим работы колеса занимает не более 1,2–2% от всего времени работы, это не вызывает беспокойства с точки зрения физической реализации движения трактора).
Основываясь на результатах описанного выше моделирования процесса работы ведущего колеса с внутренним подрессориванием, можно сделать вывод о принципиальной реализуемости идей, заложенных в конструкцию данного колеса. Однако не следует забывать, что проведенный эксперимент — все лишь моделирование в машинных условиях, и его результаты обязательно требуют подтверждения экспериментом «в железе».
5.2 Расчет навесоспособности трактора с ведущим колесом с внутренним подрессориваниемТак как у трактора с опущенной ведущей звёздочкой в связи с увеличением базы и перемещением центра тяжести, возможно, ожидать увеличение навесоспособности, необходимо произвести расчет навесоспособности по методике, предложенной в ГСКБ ВГТЗ.
Согласно ГОСТ 26817–86 навесоспособность определяется массой груза, при котором центр масс смещается на 0,2 длины опорной поверхности от середины опорной поверхности назад. Однако данная формулировка страдает некоторыми недостатками. Во-первых, смещение центра масс не вполне характеризует способность трактора нести тот или иной вес на большем или меньшем плече с сохранением минимально допустимой нагрузки на передние колёса или катки ходового аппарата. Во-вторых, в вышеприведенной редакции отсутствуют даже указания на необходимость определения навесоспособности при различных положениях центра масс орудия. А поскольку эти положения для различных операций или перемещения полезного груза существенно отличаются, то, в зависимости от конструкции ходового аппарата, механизма навески и положения центра масс трактора, превосходство одного положения навешиваемого груза над другим не гарантирует его превосходства при расположении груза на другом расстоянии от центра масс трактора. В этой связи применяемую в ряде испытательных организациях методику оценки навесоспособности, когда максимальный навешиваемый груз определяется из условия сохранения контакта передних опорных катков или колес с поверхностью или максимальной нагрузки на них, следует считать более рациональной с точки зрения объективной оценки данного свойства.
Вертикальная нагрузка, приложенная к трактору сзади и приводящая к отрыву переднего катка, определяется из условия равенства нулю суммы моментов от веса трактора и веса навешиваемого груза относительно предполагаемой оси вращения остова при опрокидывания трактора назад вокруг оси ведущей звёздочки. При этом не учитывается остающаяся неподвижной и не создающая момент часть массы трактора в виде нижней ветви гусеницы, задних опорных катков или, как в нашем случае, ведущей звездочки.
Минимальная масса груза или орудия, обуславливающая опрокидывание трактора назад определяется из выражения
|
где М — масса трактора;
х2 — расстояние от середины опорной поверхности до предполагаемой или фактической точки опрокидывания, измеренное по горизонтали;
х — горизонтальная координата центра тяжести трактора относительно середины опорной поверхности;
х1 — горизонтальная координата центра тяжести сзади расположенного орудия или груза относительно середины опорной поверхности.
Подставляя физические параметры реально существующего трактора ВТ–100 и проектируемого трактора получим:
для трактора ВТ–100
М = 8060 кг;
х2 = 615 мм;
х = 187 мм;
х1 = 3163 мм;
|
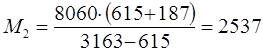 (кг).
(кг). для конструкции трактора с опущенным на грунт ведущим колесом
М = 8060 кг;
х2 = 1150 мм;
х = 98 мм;
х1 = 3500 мм;
|
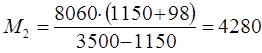 (кг).
(кг). Таким образом, навесоспособность N определится, как отношение минимальной массы груза или орудия, обуславливающей опрокидывание трактора назад к массе трактора
|
для трактора ВТ–100
![]()
для конструкции трактора с опущенным на грунт ведущим колесом
![]()
Увеличение навесоспособности вновь проектируемого трактора по сравнению с серийным трактором семейства ВТ–100 составит
|
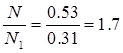 раза.
раза. Данное увеличение достаточно весомое, что является неоспоримым преимуществом, так как потребность в тракторах с повышенной навесоспособностью, как уже говорилось выше, в последнее время значительно возросла.
5.3 Расчет угловой жесткости трактора с ведущим колесом с внутренним подрессориваниемОдним из преимуществ новой конструкции, по нашим предположением, должно явиться улучшение характеристик плавности хода, что значительно улучшить ряд характеристик, связанных с условиями работы тракториста.
Параметром, непосредственно влияющим на плавность хода трактора, является угловая жесткость подвески.
Для определения данного параметра сначала необходимо найти положение центра тяжести вновь спроектированного трактора. Положение центра тяжести (центра масс) гусеничного трактора устанавливают так, чтобы получить равномерное распределение вертикальных нагрузок по опорным каткам при наиболее вероятном тяговом усилии. Оптимальная координата центра тяжести определяется из формулы
|
где Lг — длина опорной поверхности гусеницы;
hкр — высота линии тяги над плоскостью контакта колёс с почвой;
РН — номинальное тяговое усилие по типажу;
y — коэффициент перераспределения номинального усилия, равный 1,5¸1,75;
G — эксплуатационный вес трактора (см. рисунок 5.4).


Подставляя размеры конструкции трактора, получим, что центр масс располагается на расстоянии 1223 мм от оси ведущей звездочки.
Найдём угловое перемещение рамы трактора при статической нагрузке (Q=0). Считаем, что жесткость упругих элементов звёздочки равна жесткости пружин катков, то есть с1=с2=с3.
Находим расстояния от середин подрессоренных отрезков до центра масс:
![]() (мм)
(мм)
![]() (мм)
(мм)
![]() (мм)
(мм)
Угловое перемещение рамы вычислится из формулы:
|
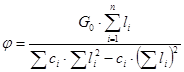 ,
, где G0 — вес подрессоренной части трактора;
|
![]() (кг)
(кг)
сi — жесткость упругих элементов;
li — расстояние от упругих элементов до центра тяжести.
Подставляя данные по конструируемому трактору в формулу (5.7) получим следующее:
|
Найдем величину углового перемещения рамы для случая движения трактора с поднятым плугом массой Q=600 кг.
Вначале определим координаты смещенного центра тяжести трактора и новые плечи — расстояния от упругих элементов трактора до центра тяжести:
|
где ![]() — горизонтальная координата сзади расположенного орудия или груза относительно середины опорной поверхности (базы) трактора;
— горизонтальная координата сзади расположенного орудия или груза относительно середины опорной поверхности (базы) трактора;
а — смещение центра тяжести;
х — горизонтальная координата центра тяжести трактора относительно середины опорной поверхности.
Согласно [11], величина горизонтальной координаты сзади расположенного орудия составит
![]() мм.
мм.
Отсюда:
|
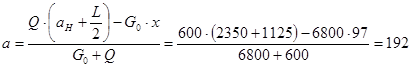 мм
мм Как и следовало ожидать, центр масс сместился по направлению к ведущей звёздочке.
Следовательно,
![]() (мм)
(мм)
![]() (мм)
(мм)
![]() (мм)
(мм)
|
![]() рад.
рад.
Угловые перемещения трактора с ведущим колесом с внутренним подрессориванием, опущенным на грунт значительно меньше соответствующих перемещений серийного трактора, что ведет к повышению угловой жесткости машины, приводящей, в свою очередь, к улучшению характеристик плавности хода.
6. Заключение
На основании вышеизложенного материала следует ряд общих выводов:
1. Сравнительный анализ и сопоставление колесных и гусеничных машин при эксплуатации их в тяжелых дорожных, а особенно во внедорожных, условиях показывает преимущество последних по таким важнейшим показателям, как проходимость, производительность, манёвренность, тягово-сцепные качества, удобство и надежность работы.
2. На эффективность работы гусеничного движителя влияет целый ряд факторов, среди которых расположение центра масс трактора, тип привода ведущего колеса, форма обвода гусеницы, тип ленты гусеницы и шаг гусеничной цепи, число опорных катков, а также некоторые другие.
3. Среди факторов, влияющих на эффективность работы гусеничного движителя можно выделить конструктивное положение ведущего колеса трактора и тип его подрессоривания.
4. Как один из способов повышения эффективности работы гусеничного движителя предложено применить ведущее колесо с внутренним подрессориванием, опущенное на грунт. Предположительно это позволит увеличить базу трактора, навесоспособность машины, угловую жесткость машины, характеристики плавности хода.
5. Патентный обзор с глубиной поиска до тридцати пяти лет показал, что существующие аналоги конструкций не применяются в силу ряда причин на гусеничных сельскохозяйственных тракторах.
6. Кинематическое исследование предложенной конструкции колеса показало принципиальную возможность реализации подобной конструкции. Выведены формулы для определения координат точек колеса в любой момент времени.
7. Анализ физической осуществимости кинематической модели колеса показал принципиальную реализуемость данной конструкции с точки зрения кинетостатики. Также рассчитан на изгиб упругий элемент, обеспечивающий подрессоривание колеса. Конструкция обладает необходимым запасом прочности.
8. С помощью средств автоматизированного проектирования смоделировано движение колеса по поверхности с неровностями. Моделирование подтвердило выводы, сделанные в предыдущих разделах.
9. Расчет навесоспособности и углового перемещения рамы трактора показал, что с применением на тракторе новой конструкции ведущего колеса, улучшается целый комплекс параметров, связанный с эффективностью работы.
10. Работа также поставила ряд вопросов перед исследователями, выраженные в необходимости проведения целого ряда расчетов и экспериментов с привлечением опытных образцов конструкции, следовательно, работа не завершена, она будет продолжена в дальнейшем и имеет большие перспективы на успех.
Список использованной литературы
1. Всероссийская сеть распространения правовой информации «КонсультантПлюс»: WEB-страница.—www.consultant.ru
2. Intellectual prophecy network: WEB-страница.—www.patent.ibm.com/ibm.html
3. А.С. 821229.СССР, МКИ3 B60 B 9/00. Упругое колесо железнодорожного транспортного средства со ступицей и обводом/ В.В.Калякин
4. А.С. 933481.СССР, МКИ3 B60 B 9/00. Металлоэластичное колесо транспортного средства/ В.В.Кацыгин, В.И.Воронцов, И.Г.Львутин, А.В.Вавилов и А.Н.Орда
5. А.С. 160082.СССР, МКИ3 B62 D 9/00. Опорный каток гусеничных машин/ В.Н.Бондарев, В.В.Гриднев, Б.В.Круглов, А.А.Незин
6. Пат. 5125443.США, МКИ3 B60 B 9/26. Spring-mounted wheel assembly/ Gil Schwartzman
7. Пат. 4553577.США, МКИ3 B60 B 9/26. Wheel structure with resilien spokes/ John D.W.Gregg
8. Платонов В.Ф. Динамика и надежность гусеничного движителя.—М.: Машиностроение, 1973.—232 с.
9. Антонов А.С. Теория гусеничного движителя.— М.: Машгиз, 1949.—354 с.
10. Медведев М.И. Гусеничное зацепление трактора.— М.: Машиностроение, 1985.— 268 с.
11. Анилович В.Я., Водолажченко Ю.Т. Конструирование и расчет сельскохозяйственных тракторов: Справочное пособие.— 2-е изд., переработ. и доп. — М.: Машиностроение, 1976.— 456 с.
12.Барский И.Б. Конструирование и расчет тракторов: Учебник для ВУЗов по специальности «Автомобили и тракторы».— 3-е изд., переработ. и доп.— М.: Машиностроение, 1980.—335 с.
13.ПлатоновВ.Ф., Леиашвили Г.Р. Гусеничные и колёсные тягово-транспорные машины.— М.: Машиностроение, 1986.—296 с.
14.Гуськов В.В. Оптимальные параметры сельскохозяйственных тракторов.— М.: Машиностроение, 1966.—195 с.
15. Гинзбург Ю.В., Швед А.И., Парфенов А.П. Промышленные тракторы.— М.: Машиностроение, 1986.—296 с.
16.Мировые достижения по пахотным гусеничным тракторам и основные направления: Методические указания/ Сост. Мезенцев М.С.—Волгоград: ВолгПИ, 1988.—40 с.
17. Ксеневич И.П. и др. Ходовая система—почва—урожай/ И.П. Ксеневич, В.А. Скотников, М.И. Ляско.— М.: Агропромиздат, 1985.—304 с.
18.Барский И.Б., Анилович В.Я., Кутьков Г.М. Динамика трактора.— М.: Машиностроение, 1973.—280 с.
19.Тракторы. Проектирование, конструирование и расчёт/ Под ред. И.П. Ксеневича. М.: Машиностроение, 1991.—544 с.
20. Гуськов В.В., Коммисарчук А.М. К вопросу выбора оптимального положения центра тяжести гусеничного трактора.— В кн. Механизация и электрификация сельского хозяйства, Минск: Вышейшая шкла, 1968, вып.1.— с. 38–39
21.Мацепуро М.Е., Порошков В.А. Влияние положения центра тяжести и центра давления болотного трактора на его проходимость и тяговые качества.— В кн. Вопросы земледельческой механики. Т. 3. Минск: Гос. изд. БССР, 1960.— с.353-377
22. Фесик С.П. Справочник по сопротивлению материалов.— Киев: Будивельник, 1970.—674 с.
23. Фирма Valtra Vamet и её новые тракторы: Отчет/ НАТИ; А.П.Парфенов.—М., 1999.—143 с.
24. Тракторы фирмы New Holland с автоматическим включением привода переднего моста: Отчет/ НАТИ; А.П.Парфенов.—М., 1999.—96 с.
25. Будущее трансмиссий сельскохозяйственных тракторов за бесступенчатыми передачами: Отчет/ НАТИ; М.Я.Мининзон.—М., 1999.—136 с.
26. Забавников Н.А. Основы теории транспортных гусеничных машин.—М.: Машиностроение, 1968
27. Кушнарёв А.С. Конференция по проблеме уплотняющего воздействия на почву ходовых систем.— М.: Тракторы и сельхозмашины, 1981, № 3.— с.38–39
Похожие работы
... новых типов гусеничных движителей, а также модернизации старых, с целью увеличения КПД движителя следует в первую очередь обратиться к работам [8, 9, 10]. В них широко рассматриваются как теоретические вопросы работы гусеничного движителя, так и практические задачи по решению проблем потери мощности в движителе, долговечности гусеничного движителя, динамики взаимодействия гусениц с направляющим и ...
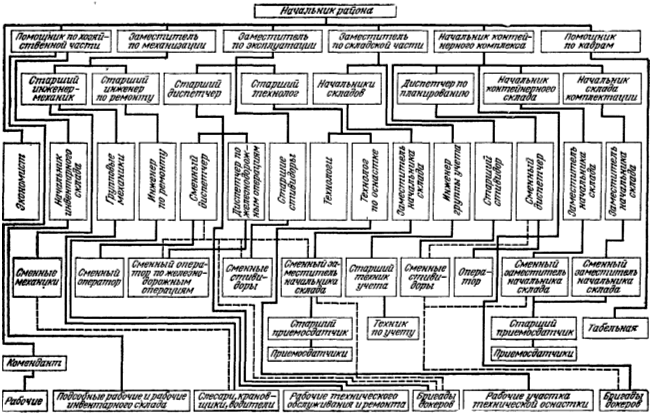
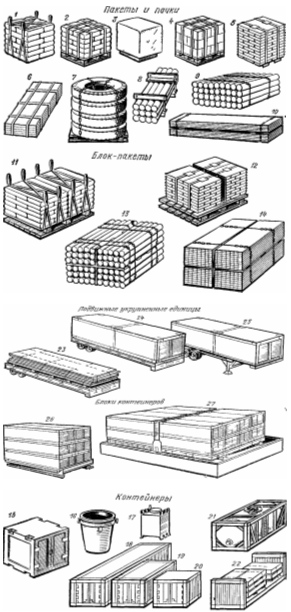
... навыки у докеров. 23. СИСТЕМА ОБЕСПЕЧЕНИЯ ПЕРЕГРУЗОЧНЫХ РАБОТ ТЕХНОЛОГИЧЕСКОЙ ОСНАСТКОЙ Система обеспечения оснасткой технологических процессов портовых перегрузочных работ включает: планирование поставки и производство механизмов и приспособлений; содержание их в исправном состоянии, т. е. регистрацию, освидетельствование с испытанием, периодические осмотры, техническое обслуживание и ...
... и по нашему мнению одним из важнейших элементов увеличения прибыльности производства продукции растениеводства является повышение эффективности использования машинно-тракторного парка предприятий. В процессе преддипломной практики нами было обследовано предприятие, располагающееся в Краснодарском крае Ленинградского района. Бывший колхоз-гигант, разделенный в последствии на несколько отдельных ...
... % вместо 31,3 % в 2006 г. ЗАКЛЮЧЕНИЕ Цель первой части комплексной дипломной работы состояла во всестороннем анализе и оценке результатов функционирования растениеводства ООО "Прогресс-Агро" Песчанокопского района Ростовской области, выявлении нерешенных проблем отрасли, обосновании финансовых и связанных с ними организационно-управленческих мероприятий по повышению ее экономической эффектив





0 комментариев