Координаты и график кривой разгона для внутреннего канала
Координаты и график кривой разгона основного контура
Интерполяция по трем точкам
Линейное сглаживание и график кривой разгона для внутреннего контура
Линейное сглаживание и график кривой разгона по основному каналу
Нормирование кривых разгона
Нормированная кривая разгона для внутреннего контура
Нормированная кривая разгона по основному каналу
Аппроксимация методом Симою
S + 60.75 s + 13.5 s + 1 38.1160 s + 10.6679 s + 1
Навигация
S + 60.75 s + 13.5 s + 1 38.1160 s + 10.6679 s + 1
Расчет настроек автоматического регулятора
22145
знаков
10
таблиц
36
изображений
91.125 s + 60.75 s + 13.5 s + 1 38.1160 s + 10.6679 s + 1
Анализируя таблицу можно сделать вывод о том, что передаточные функции второго порядка практически одинаковы, а третьего порядка значительно отличаются.
6.5 Сравнение экспериментальных и фактических кривых разгона.
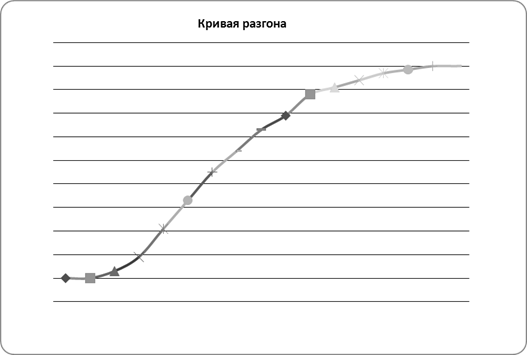
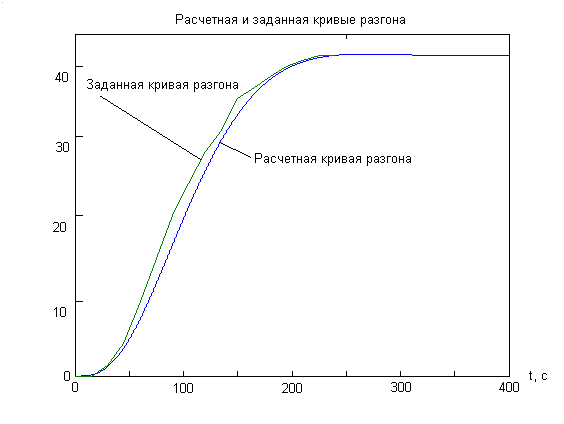
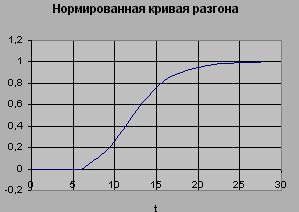
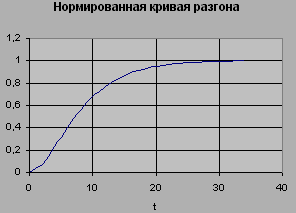
Для исходных передаточных функций с помощью программы ASR, пунктов аппроксимация (создать передаточную функцию и изменить время) получим координаты кривых разгона и сравним их с экспериментальной кривой:
- по внешнему контуру
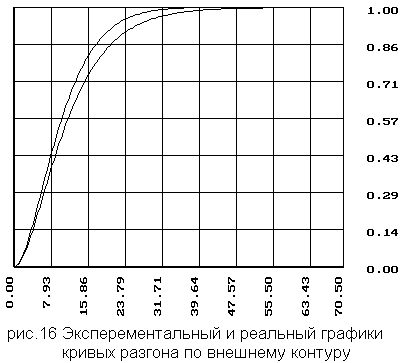
- по внутреннему контуру
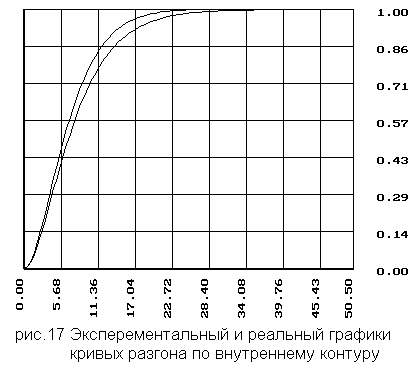
- по основному каналу
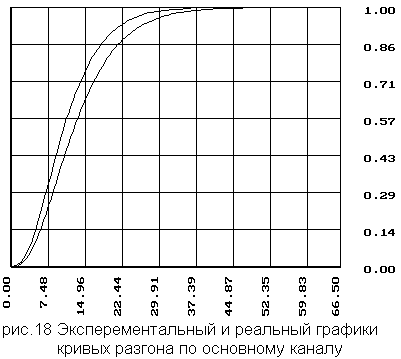
Полученные значению передаточных функций не значительно отличают от фактических, что говорит о достаточно не большой погрешности между фактическими и экспериментальными данными.
Расчет одноконтурной АСР методом Роточа.
В программе Linreg задаем параметры объекта. Выбираем в качестве регулятора ПИ- регулятор. И рассчитываем его настройки:
а) для экспериментальной передаточной функции.
В программе Linreg задаем передаточную функцию объекта второго порядка с запаздыванием. Выбираем ПИ-регулятор и определяем его настройки.
Получаем kp = 1.0796
Tu = 8.0434
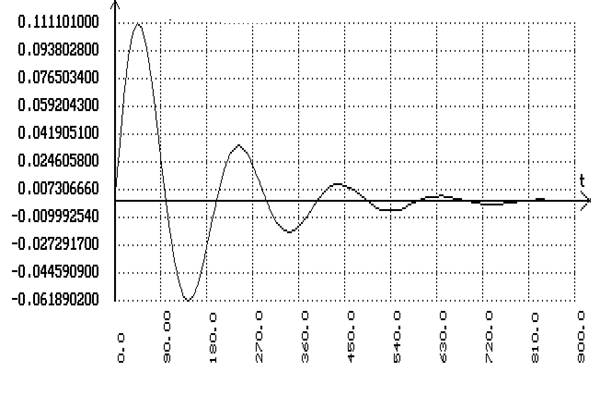
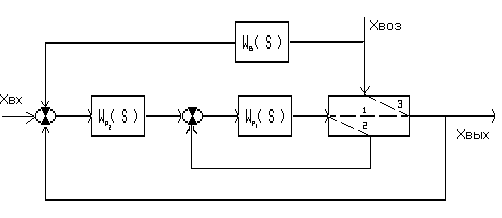
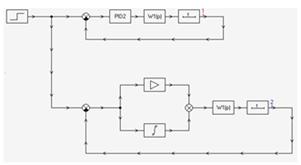
В программе SIAM пользуясь следующей схемой для одноконтурной системы
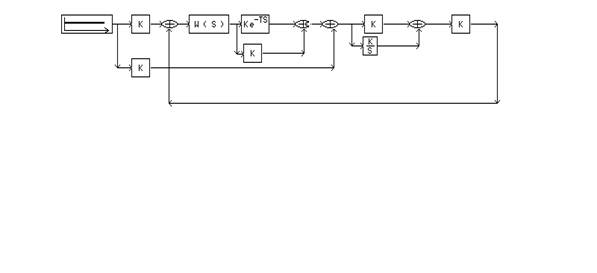
Подаем скачек на сумматор, стоящий после запаздывания и получаем график переходного процесса по заданию:
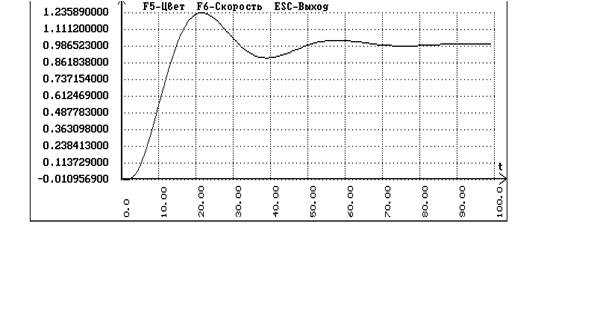
Подаем скачек на сумматор, стоящий перед объектом и получаем график переходного процесса по возмущению:
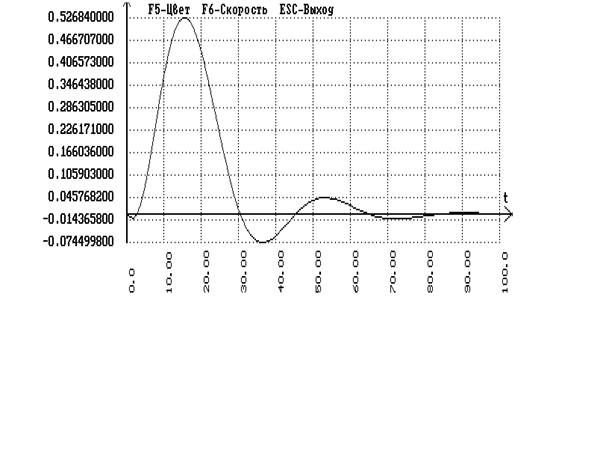
б) для фактической передаточной функции
В программе Linreg задаем передаточную функцию объекта третьего порядка с запаздыванием. Выбираем ПИ-регулятор и определяем его настройки.
Получаем kp = 0.8743
Tu = 8.3924
В программе SIAM пользуясь схемой для одноконтурной системы получаем
- переходный процесс по заданию:
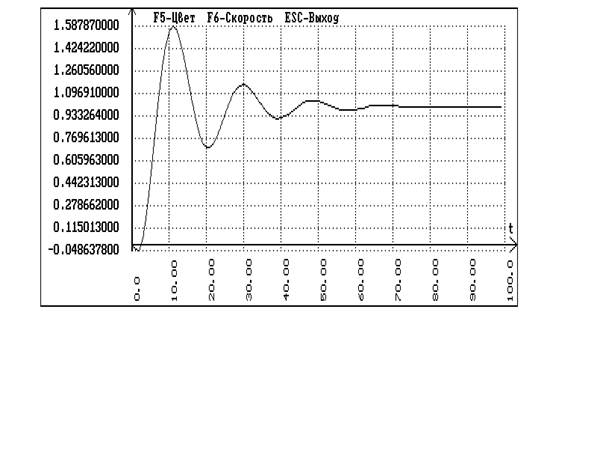
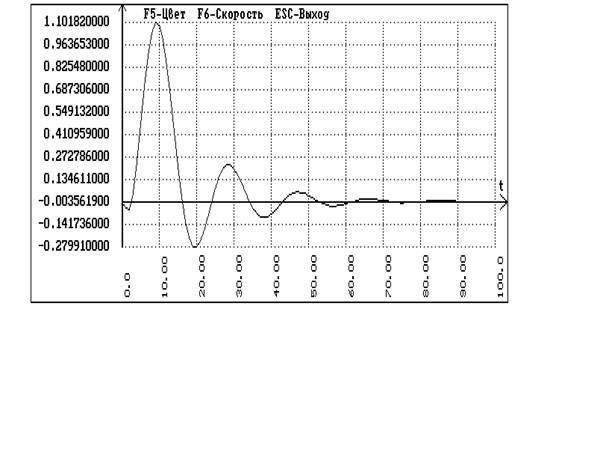
Расчет каскадной АСР методом Роточа.
а) для экспериментальной передаточной функции.
Первоначально определим настройки внутреннего регулятора для внутреннего контура с передаточной функцией W1(s).
0.4s + 1
W1(s) = --------------------------
2
14.0904s + 6.9614s +1
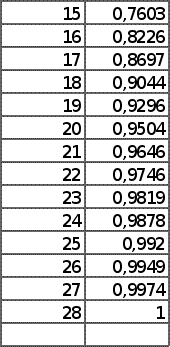
С помощью программы ASR получим АФХ по передаточной функции и определим значения u(m,w), v(m,w), a(m,w), w.
| v(m,w) | u(m,u) | a(m,w) | w | kp | Tu |
| 1,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
| 1,0211 | -0,0678 | 1,0234 | 0,0100 | 15,0783 | 0,0109 |
| 1,0360 | -0,1398 | 1,0454 | 0,0200 | 7,4774 | 0,0211 |
| 1,0439 | -0,2151 | 1,0659 | 0,0300 | 4,9709 | 0,0307 |
| 1,0442 | -0,2931 | 1,0845 | 0,0400 | 3,7336 | 0,0395 |
| 1,0361 | -0,3728 | 1,1012 | 0,0500 | 3,0067 | 0,0475 |
| 1,0194 | -0,4531 | 1,1156 | 0,0600 | 2,5367 | 0,0547 |
| 0,9936 | -0,5329 | 1,1275 | 0,0700 | 2,2147 | 0,0609 |
| 0,9587 | -0,6108 | 1,1368 | 0,0800 | 1,9877 | 0,0660 |
| 0,9147 | -0,6857 | 1,1431 | 0,0900 | 1,1826 | 0,0701 |
| 0,8619 | -0,7559 | 1,1464 | 0,1000 | 1,1713 | 4,4754 |
| 0,8008 | -0,8203 | 1,1464 | 0,1100 | 1,6386 | 4,5739 |
| 0,7323 | -0,8775 | 1,1429 | 0,1200 | 1,1584 | 0,0749 |
| 0,6576 | -0,9263 | 1,1360 | 0,1300 | 1,5905 | 0,0737 |
| 0,5778 | -0,9658 | 1,1254 | 0,1400 | 1,6169 | 0,0711 |
| 0,4945 | -0,9953 | 1,1114 | 0,1500 | 1,6842 | 0,0668 |
| 0,4095 | -1,0143 | 1,0938 | 0,1600 | 1,8064 | 0,0609 |
| 0,3243 | -1,0229 | 1,0731 | 0,1700 | 2,0137 | 0,0533 |
| 0,2407 | -1,0214 | 1,0493 | 0,1800 | 2,3750 | 0,0438 |
| 0,1601 | -1,0103 | 1,0229 | 0,1900 | 3,0885 | 0,0324 |
| 0,0840 | -0,9906 | 0,9942 | 0,2000 | 5,0095 | 0,0000 |
| 0,0134 | -0,9635 | 0,9635 | 0,2100 | 26,1125 | 0,0034 |
Так как настройки регулятора не могут быть отрицательными то ограничимся 3 квадрантом. И с помощью программы на BASIC рассчитаем оптимальные настройки для ПИ - регулятора методом Стефани по следующим формулам:
A^2(m,w) m 1
Tu = ------------------------ , kp = ---------- - ----------
w(m^2+1)* v(m,w) v(m,w) u(m,w)
наибольшее отношение kp/Tu и будет оптимальными настройками.
Получили что kp = 1.712763
Tu = 4.47537
В программе SIAM с помощью схемы для одноконтурной системы без запаздывания получаем переходные процессы по заданию и по возмущению:
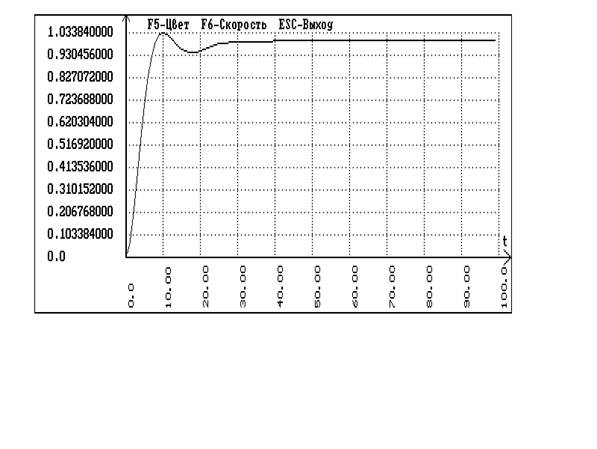
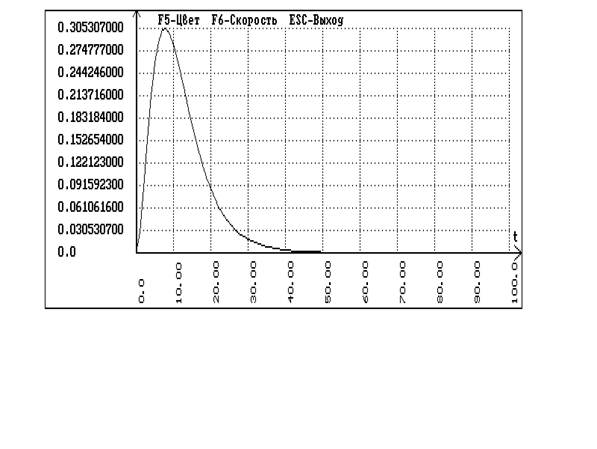
Сравнивая график кривой разгона по основному каналу и переходный процесс внутреннего контура каскадной системы делаем вывод о том, что за время запаздывания основного контура переходный процесс во внутреннем контуре затухнуть не успевает, следовательно передаточная функция эквивалентного объекта имеет вид:
Wоб(s) * Wp1(s)
Wоб(s) = --------------------------- =
1 + Wоб1(s) * Wp1(s)
1 1
--------------------------------- * (1,7128 + ---------- )
2 4,4754s
38,1160s + 10,6679s + 1
-------------------------------------------------------------- =
0,4s + 1 1
1 + --------------------------- * (1,7128 + ----------)
2 4,4754s
14,0904s + 6,9614s + 1
3 2
107.9987s + 67.4444s + 14.6247s + 1
= ---------------------------------------------------------------------------
5 4 3 2
4116.4785s + 3186.9547s + 969.316s + 138.1861s + 15.7294s + 1
Определяем настройки ведущего регулятора. Для ПИ-регулятора получаем:
kp = 0.1249
Tu = 5.4148
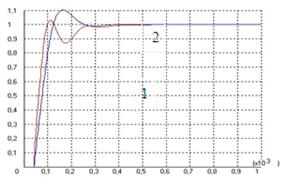
В программе SIAM с помощью схемы каскадной системы получаем переходный процесс по заданию:
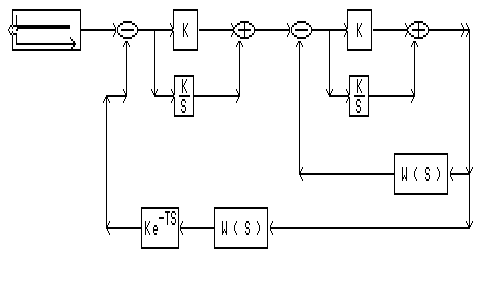
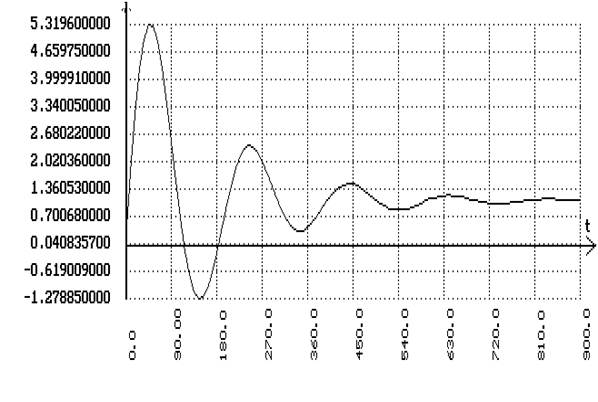
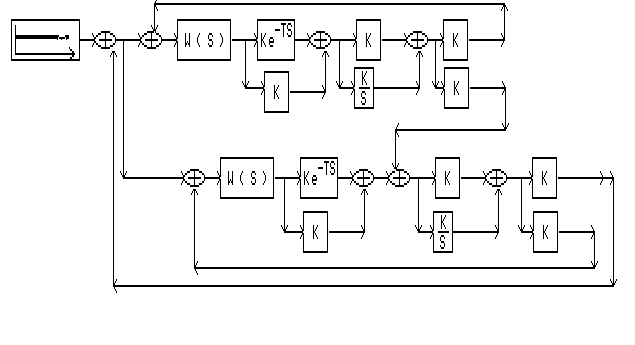
С помощью схемы каскадной системы получаем переходный процесс по возмущению:
б) для реальной передаточной функции.
Определим настройки внутреннего регулятора для объекта второго порядка с передаточной функцией
1
W1(s) =-------------------------
2
16,1604s + 8.04s + 1
Получаем следующие настройки регулятора: kp = 4.3959
Tu = 6.5957
В программе SIAM пользуясь схемой одноконтурной системы без запаздывания получаем графики переходных процессов по заданию и по возмущению:
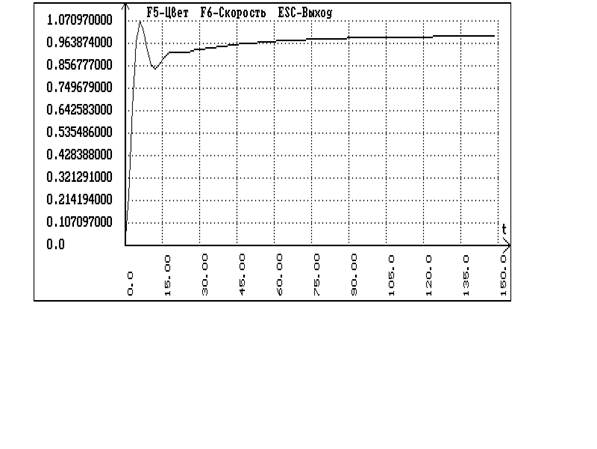
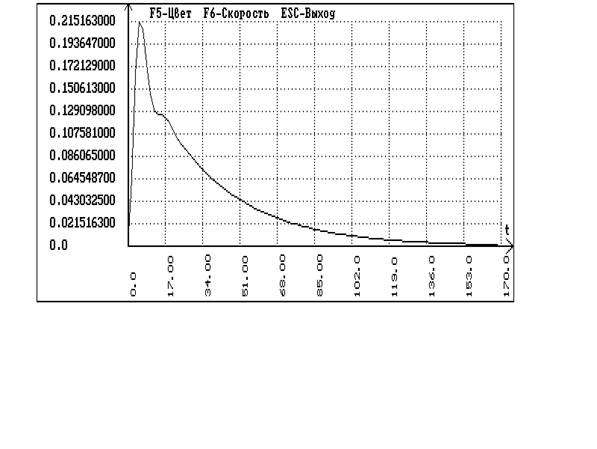
Сравнивая график кривой разгона по основному каналу и переходный процесс внутреннего контура каскадной системы делаем вывод о том, что за время запаздывания основного контура переходный процесс во внутреннем контуре затухнуть не успевает, следовательно передаточная функция эквивалентного объекта имеет вид:
Wоб(s) * Wp1(s)
Wоб(s) = --------------------------- =
1 + Wоб1(s) * Wp1(s)
1 1
--------------------------------- * (4.3959 + ---------- )
3 2 6.5957s
91.125s + 60.75s + 13.5s + 1
-------------------------------------------------------------- =
1 1
1 + ------------------------ * (4.3959 + ----------)
2 6.5957s
16.1604s + 8.04s + 1
3 2
468.5449s + 249.2673s + 37.0334s + 1
= --------------------------------------------------------------------------------------------
6 5 4 3 2
42696.154s + 49705.969s + 25770.6474s + 7229.3112s + 1076.6779s+71.4868s+ 1
Определяем настройки ведущего регулятора. Для ПИ-регулятора получаем:
kp = 1.2822
Tu = 6.3952
В программе SIAM с помощью схем для каскадной системы получим переходные процессы по заданию и по возмущению:
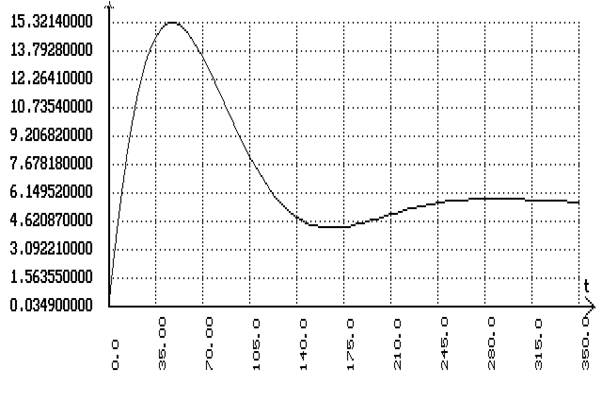
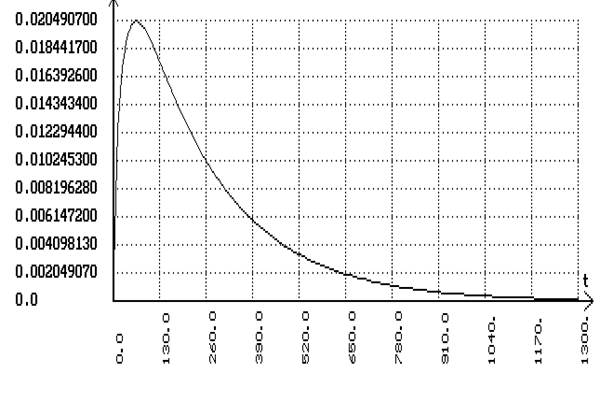
Расчет комбинированной АСР.
а) для эксперементальной передаточной функции
Расчет компенсирующего устройства
В программе SIAM с помощью смоделированной схемы комбинированной системы без компенсатора получим соответствующий переходный процесс:
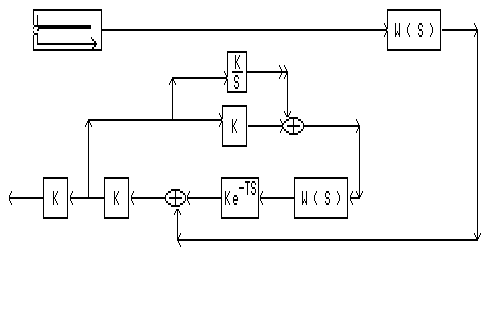
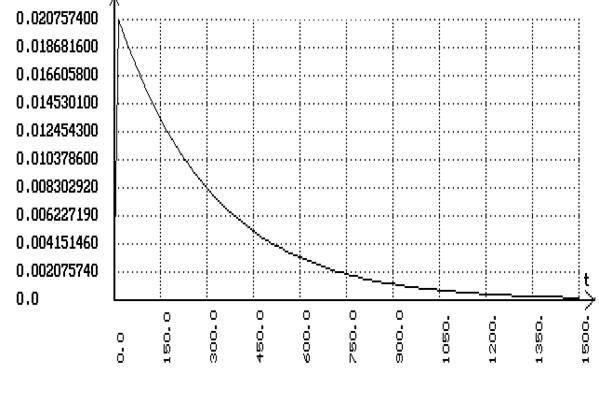
Определим передаточную функцию фильтра для структурной схемы где выход компенсатора поступает на вход регулятора по формуле:
Wов(s)
Wф(s) = --------------------- ,
Wоб(s) * Wр(s)
где Wов(s) - передаточная функция канала по возмущению,
Wоб(s) - передаточная функция объекта,
Wp(s) - передаточная функция регулятора
0,6887s + 1
-----------------------------
2
30.8783 s + 10.2426 s + 1
Wф(s) = ---------------------------------------------------------- =
1 1
------------------------------- * (1.0796 + ---------- )
2 8.0434 s
38.8783 s + 10.6679 s + 1
4 3 2
232.5099 s + 40.1406 s + 98.6173 s + 8.6837 s
= -----------------------------------------------------------
3 2
268.1379 s + 119.8220 s + 18.9263 s + 1
Настроечные параметры компенсирующего устройства будут оптимальными, если АФХ фильтра равны нулю при нулевой и резонансной частоте.
б) для реальной передаточной функции
Похожие работы
... : Сравнивая экспериментальные и фактические кривые разгона видим, что они отличаются очень сильно. Фактическая кривая разгона приходит к 1 на много быстрее, чем экспериментальная. Расчет АФХ передаточных функций. 1. Объект второго порядка по возмущению: а) экспериментальная: 1 1,0000 0,0000 34 -0,3751 -0,5372 68 -0,1944 -0,0241 2 1,0211 -0, ...
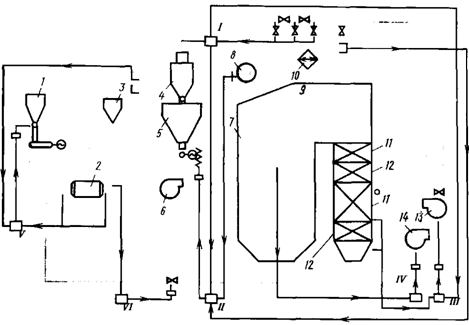
... на основе правил Госгортехнадзора с учетом местных условий и особенностей оборудования. Котел должен быть оборудован необходимым количеством контрольно-измерительных приборов, автоматической системой регулирования важнейших параметров котла, защитными устройствами, блокировкой и сигнализацией. Режимы работы котла должны соответствовать режимной карте, в которой указываются рекомендуемые ...
... компенсатора 1.W(s)=1/(9*s2+6*s+1) 2.K=Kп=0.49 3.K/S=Kп/Tи=0.0916 4.W(s)=1/(13.824*s3*17.28*s2+7.2*s+1) 5.K=1,T=6 6.K=-1 7.K=-1 Переходной процесс Перерегулирование – 87% Время затухания – 65с Степень затухания –0.95 9.2 Комбинированная система управления с подачей дополнительного воздействия на вход регулятора Определим передаточную функцию фильтра согласно формуле :Wф(s)=Wов(s)/( ...
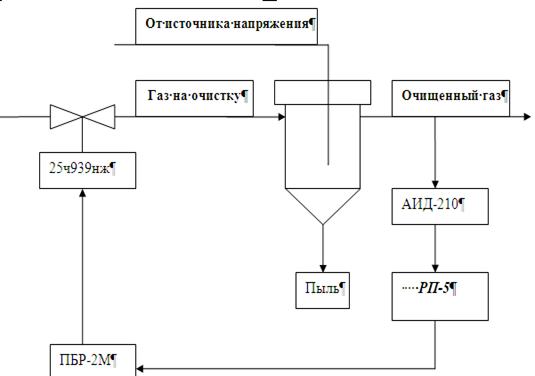
... параметры. Показателем эффективности данного процесса является степень очистки газа. Для решения задачи построена одноконтурная система управления процессом электрической очистки газа. Выбран регулятор и построена математическая модель системы управления. На модели определены оптимальные параметры регулятора. Выбраны приборы для основного контура регулирования. 1. Специальная часть ...
0 комментариев