РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ

4. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ФИЛЬТРОВ.

Для выделения колебаний заданных частот необходимо рассчитать полосовые фильтры, у частотных характеристик которых центры эффективного пропускания совпадали бы с этими частотами.

В качестве полосовых фильтров используются полиномиальные фильтры Чебышева. Каждый фильтр выделяет свою гармонику. Поскольку гармоники сигнала на выходе нелинейного преобразователя достаточно далеко разнесены по частоте, порядок фильтра получается невысоким. Частоты соседних гармоник должны попадать в полосу непропускания фильтра. Характеристика ослабления фильтра должна обладать геометрической симметрией относительно выделяемой гармоники.

Расчет полосового фильтра обычно сводят к расчету НЧ-прототипа.

Технические требования к фильтру: N=2 – номер выделяемой гармоники, U_{m вых}=8В – выходное напряжения фильтра, ΔА=1дБ – неравномерность ослабления в полосе пропускания (ослабление полезных гармоник), А_min=20дБ – ослабление в полосе непропускания (степень подавления мешающих гармоник), U_{пит ф}=12В – напряжение питания операционного усилителя. Частота второй гармоники при частоте генерируемых колебаний 100кГц ровна 200кГц, следовательно, f₀=200кГц.

Для определения нормированной частоты НЧ-прототипа - Ω₃, соответствующей границе полосы эффективного непропускания (в дальнейшем ПЭН), необходимо воспользоваться зависимостями D=F(А_min), графики которых изображены на Рис 2.12 [1]. При этом вначале по заданным значениям ΔА и А_min определяем вспомогательную функцию D=25, а затем, задаваясь приемлемым значением порядка фильтра-прототипа n=3, для полученного значения D по Рис.2.13[1], определяем Ω₃=1,4.

(23)

Рассчитаем граничные частоты полосы эффективного пропускания (в дальнейшем ПЭП) и ПЭН.

(24)

Зная соотношение для ω₀:
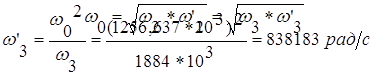То, задавшись одним из четырех неизвестных частот, например, примем что f₃=300 кГц, то есть ω₃=2πf₃=1884000 рад/с, найдем ω′₃:

Учитывая соотношение:

	(25)
	(26)
	(27)
	(28)

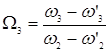
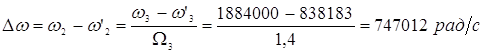Найдем ширину полосы эффективного пропускания – Δω:
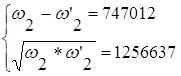Получаем систему уравнений:

Решая данную систему, получаем:

ω₂=937464,6 рад/с

ω′₂=1684476 рад/с

Таким образом, граничные частоты ПЭП и ПЭН принимают значения:

f₂=ω₂/2π=150 кГц (ω₂=937464,6 рад/c );

f′₂=ω′₂/2π=268 кГц (ω′₂=1684476 рад/с);

f₃=ω₃/2π=300 кГц (ω₃=1884000 рад/с);

f′₃=ω′₃/2π=133,5 кГц (ω′₃=838183рад/с).

Пользуясь таблицей 3.5 [1], по заданному ΔА и выбранному порядку находим полюсы передаточной функции НЧ-прототипа: S_1,2=-0,494171 и S_3,4=-0,247085±j0,965999.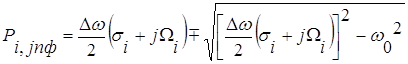
Денормирование и конструирование передаточной функции искомого ПФ осуществляется в два этапа. На первом этапе находим полюсы передаточной функции полосового фильтра по известным полюсам НЧ-прототипа. Для этого воспользуемся соотношением:

где Δω/2=373506 рад/с;

ω₀²=157,9∙10¹⁰(рад/с)²;

σ_i+jΩ_i – i-ый полюс передаточной функции НЧ-прототипа.

Учитывая, что одной паре комплексно-сопряженных полюсов передаточной функции НЧ-прототипа соответствует две пары комплексно-сопряженных полюсов передаточной функции полосового фильтра, рассчитаем полюса передаточной функции, воспользовавшись формулой (28):

Таблица 4

Результаты расчетов полюсов передаточной функции сведем в таблицу 4:

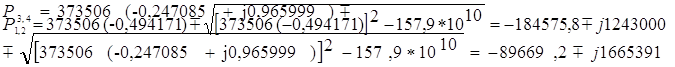
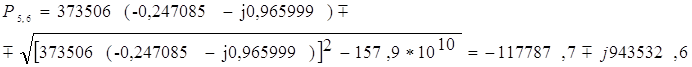
Номер полюса	Полюсы Н(р) полосового фильтра
	-α∙105	±jω∙105
1,2	1,84	12,43
3,4	0,89	16,65
5,6	1,18	9,43

(33)

На втором этапе передаточная функция полосового фильтра может быть представлена в виде произведения четырех сомножителей второго порядка:
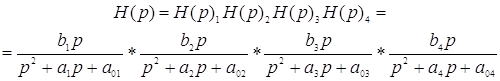Каждый сомножитель соответствует одной паре комплексно сопряженных полюсов. Коэффициенты числителя и знаменателя определяются из следующих соотношений:
Где e - коэффициент неравномерности ослабления в полосе пропускания.

где α_i и ω_i – действительная и мнимая части i-го полюса передаточной функции полосового фильтра.

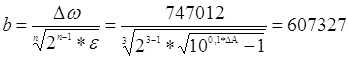
Рассчитанные коэффициенты передаточной функции запишем в таблицу 5:

Номер сомножителя	Значения коэффициентов
	bi	ai	a0i
1	607327	3,68∙105	169,4∙1010
2	607327	1,78∙105	280,4∙1010
3	607327	2,36∙105	94,5∙1010

(39)

Передаточная функция искомого ПФ:
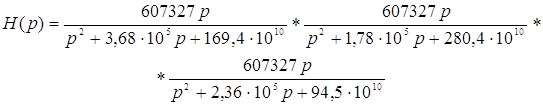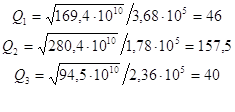Каждый сомножитель передаточной функции реализуется в виде ARC-цепи второго порядка, соответствующие звенья соединяются каскадно в порядке возрастания их добротностей. Для реализации полученной функции необходимо выбрать тип звеньев, для чего рассчитываются добротности полюсов соответствующих сомножителей, используя соотношение:

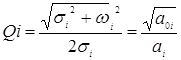
Из таблицы 3.6[1] по значениям Q выбираем схему 3. Передаточная функция, которой выглядит следующим образом:

	(37)

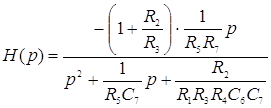Для расчета элементов звена, соответствующего первому сомножителю Н(р), составим систему уравнений:

(40)

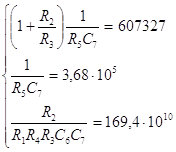
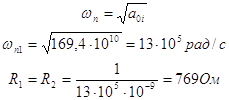Зададимся C₆=C₇=C=10нФ, тогда R₁=R₂=1/ω_пС, где ω_п – частота полюса, которая определяется по формуле:

(44)

(43)

(42)

(41)

Решая систему относительно R₅,R₃,R₄ получим: R₅=3кОм; R₃=961Ом; R₄=610Ом.
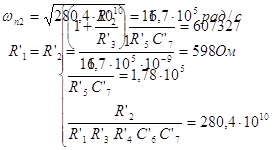Для расчета элементов второго звена ПФ составим систему уравнений:

Частота полюса и сопротивления R′₁ и R′₂ определяются так:

Решая систему относительно R′₅, R′₃, R′₄ получим: R′₅=5,6кОм; R′₃=249Ом; R′₄=1,4кОм.

Для расчета элементов третьего звена ПФ составим систему уравнений:

	(45)

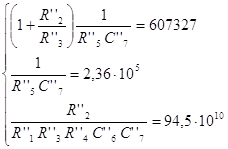Частота полюса и сопротивления R′′₁ и R′′₂ определяются так:
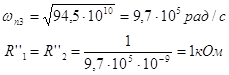Решая систему относительно R′′₅, R′′₃, R′′₄ получим: R′′₅=4,2кОм; R′′₃=666 Ом; R′′₄=1,6 кОм.

Таблица 6

Рассчитанные значения элементов звеньев ПФ запишем в таблицу 6:

	R1 Ом	R2 Ом	R3 Ом	R4 Ом	R5 кОм	C6 нФ	C7 нФ
1ое звено	769	769	961	610	3,0	10	10
2ое звено (′)	598	598	249	1400	5,6	10	10
3е звено (′′)	1000	1000	666	1600	4,2	10	10

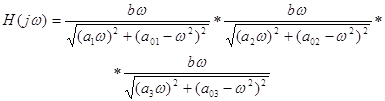Расчет АЧХ и ослабления (А) производится на основе полученной при аппроксимации рабочей передаточной функции Н(р), путем замены р=јω:

(51)

Ослабление фильтра связано с АЧХ выражением:

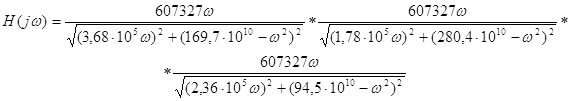
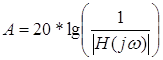Найдем частоты ПЭП, при которых ослабление (А) и АЧХ принимают минимальные и максимальные значения. Для нахождения соответствующих частот характеристики ПФ используется формула:

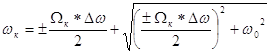где Δω=747012 рад/с – ширина ПЭП;

ω₀=1256637,04 рад/с.

Из таблицы 3.8[1] для характеристик НЧ-прототипа выбираем Ω_к для n=3: Ω_1max=0,5; Ω_1min=0; Ω_2max=1; Ω_2min=0,866.

Таблица 7

Используя формулы рассчитаем значения Н(јω) и А для всех выше рассчитанных частот, результаты расчета запишем в таблицу7:

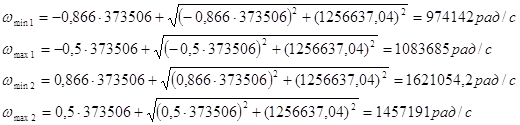
ω	ω′3	ω′2	ωmin1	ωmax1	ω0	ωmax2	ωmin2	ω2	ω3
ω (рад/с)	838183	937464,6	974142	1083685	1256637	1457191	1621054	1684476	1884000
f(кГц)	134	150	155	172,5	200	232	258	268	300
H(jω)1	0,32	0,82	0,8	1,5	2,0	1,35	0,72	0,84	0,33
H(jω)2	0,24	0,49	0,5	0,52	0,63	1,2	1,9	1,7	0,23
H(jω)3	1,3	2,26	2,5	1,12	0,79	0,55	0,7	0,63	1,29
A1	9,9	1,7	1,9	-3,5	-6,0	-2,6	2,6	1,5	9,6
A2	12,4	6,2	6,0	5,6	4,0	-1,6	-5,6	-4,6	12,7
A3	-2,3	-7,0	-7,9	-1,1	2,0	5,1	3,0	4,0	-2,2
H(jω)пф	0,09	0,9	1	0,9	1	0,9	1	0,9	0,09
(53)   A	20	1	0	1	0	1	0	1	20

По результатам Таблицы 7 построим графики Рис.12 и Рис.13.

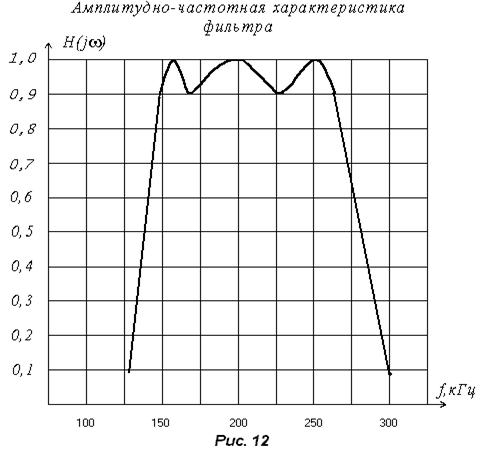
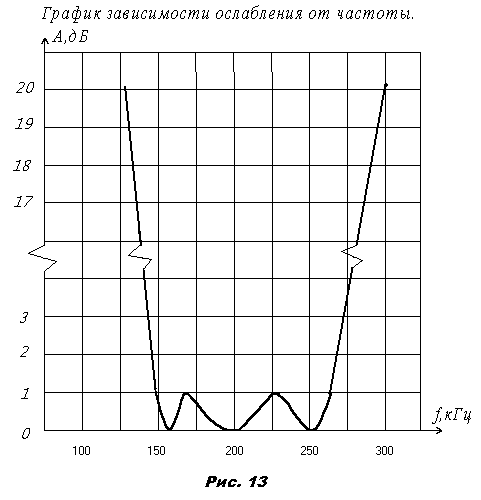
На этом расчет фильтра можно считать законченным на Рис.14 изображена схема рассчитанного фильтра.

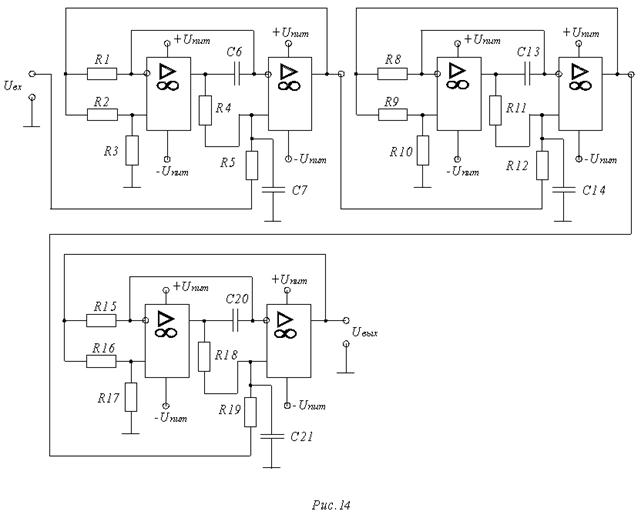
5.РАСЧЕТ ВЫХОДНОГО КАСКАДА.

(55)

(54)

(53)

Требуемое выходное напряжение устройства выделения второй гармоники U_mвых=1В (амплитудное значение). Из предыдущих расчетов известно, что амплитуда напряжения второй гармоники U₂=0,13В. Тогда амплитуда на выходе фильтра будет:

Требуемый коэффициент усиления:

Выбираем схему выходного усилителя 1 из таблицы 3.7[1]:

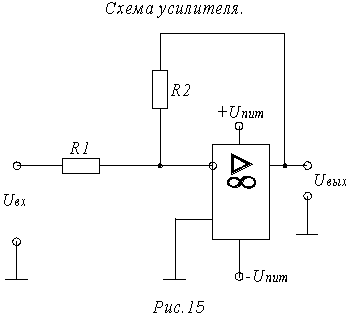
Передаточная функция схемы изображенной на Рис.15:

Зададимся значением R₁=3кОм, тогда:

6.ЗАКЛЮЧЕНИЕ.

В ходе данной работы было разработано устройство, вырабатывающее сетку частот схема которого приведена на странице 28. Был произведен расчет всех элементов разработанной схемы.

В ходе выполнения данной работы мною были приобретены навыки по расчету и разработке устройств связи.

7.СПИСОК ЛИТЕРАТУРЫ

1. Б. И. Крук, О. Б. Журавлева, М. И. Сметанина. Расчет элементов и узлов аппаратуры связи: Методические указания к курсовой работе. Новосибирск, 1997.

2. В. П. Бокалов, А. А. Игнатов, Б. И. Крук. Основы теории электрических цепей и электроники: Учебник для высших учебных заведений. – М.: Радио и связь, 1989.