Навигация
Фронт волны. Волновая поверхность
4. Фронт волны. Волновая поверхность.
При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.
Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом.
Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью.
Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.
При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются лучами. В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.
Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.
Если известно
положение
фронта волны
в некоторый
момент времени и скорость
волны ![]() , то его положение
в последующий
момент времени можно
определить
на основе принципа
Гюйгенса. Согласно этому
принципу все
точки поверхности
волнового
фронта являются
источниками
вторичных
волн. Искомое
положение
волнового
фронта совпадает
с поверхностью,
огибающей
фронты вторичных
волн.
, то его положение
в последующий
момент времени можно
определить
на основе принципа
Гюйгенса. Согласно этому
принципу все
точки поверхности
волнового
фронта являются
источниками
вторичных
волн. Искомое
положение
волнового
фронта совпадает
с поверхностью,
огибающей
фронты вторичных
волн.
5. Уравнение бегущей волны.
Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.
Так, для волн в твердом теле такой величиной является смещение от положения равновесия любой точки тела в произвольный момент времени. Для характеристики продольных волн в жидкости или газе используют понятие избыточного давления. Избыточное давление равно разности между давлением в данный момент времени, когда по среде проходит волна, и равновесным, когда возмущений в среде нет.
Получим уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным (см. определения выше). Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О - центр (источник) колебаний, она колеблется по закону:
![]() ,
,
где ![]() - смещение точки
О от положения
равновесия,
- смещение точки
О от положения
равновесия,
![]() -
частота, А –
амплитуда колебаний. Часы
или секундомер
№1 включаются
сразу, как только
начинаются
колебаний точки
О, и отсчитывают
время t
(Рисунок 2.1.1). Ось
ОУ совпадает
с направлением
распространения
волны.
-
частота, А –
амплитуда колебаний. Часы
или секундомер
№1 включаются
сразу, как только
начинаются
колебаний точки
О, и отсчитывают
время t
(Рисунок 2.1.1). Ось
ОУ совпадает
с направлением
распространения
волны.
Через
промежуток
времени ![]() процесс колебаний
дойдет до точки
В, и она будет
колебаться
по закону:
процесс колебаний
дойдет до точки
В, и она будет
колебаться
по закону:
![]() .
.
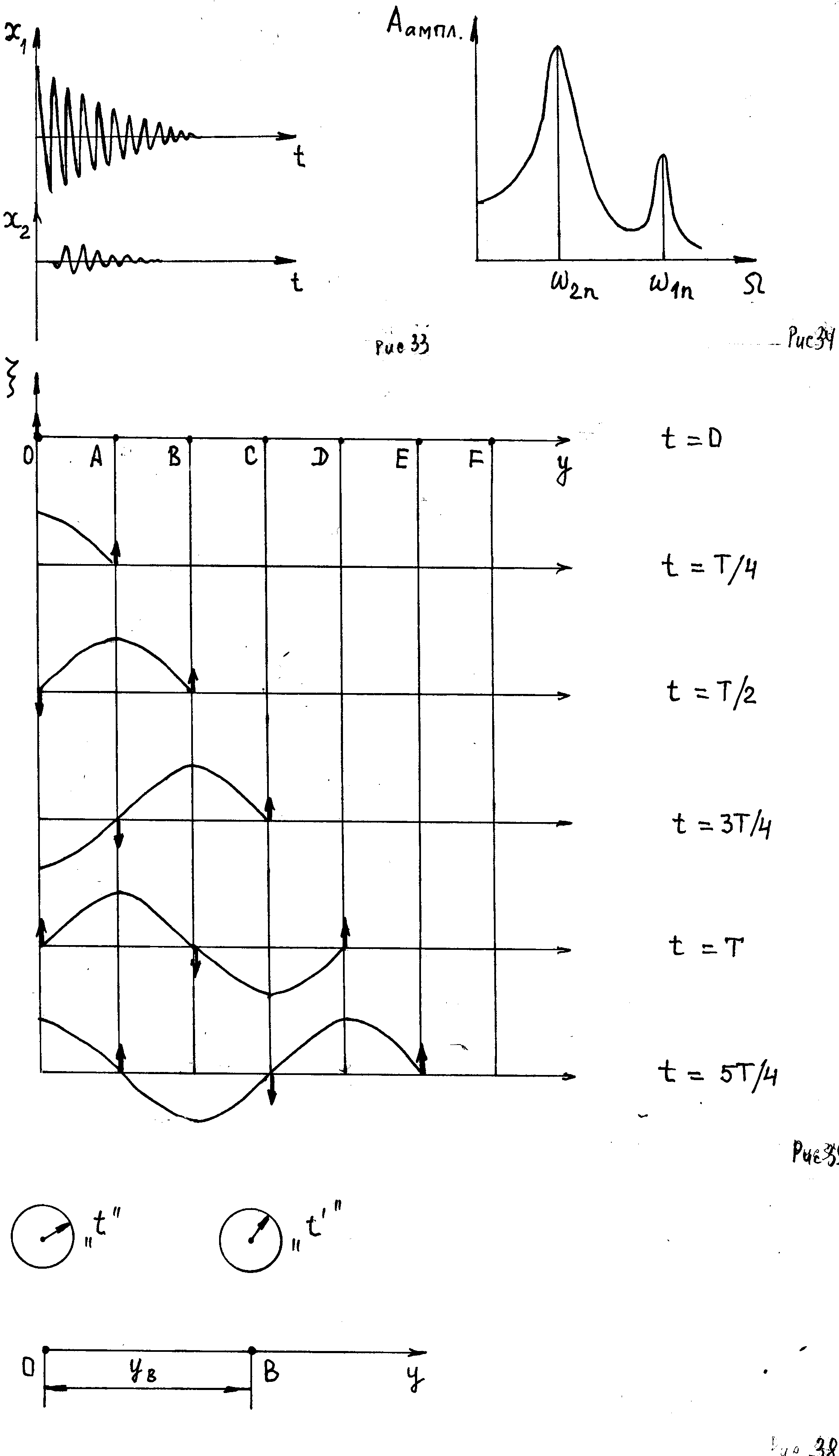
Рисунок 2.1.1.
Амплитуда
колебаний в
случае отсутствия
затухания
процесса будет
такой же как
и амплитуда
точки О. Часы
или секундомер
№2 включаются
тогда, когда
колебательный
процесс дойдет
до точки В (т.е.
когда начинает
колебаться точка В), и отсчитывают
время ![]() .
Моменты времени
t и
.
Моменты времени
t и ![]()
![]() связаны
между собой
соотношением
связаны
между собой
соотношением
![]() или
или ![]() .
Расстояние
между точками
О и В обозначим
.
Расстояние
между точками
О и В обозначим
![]() .
Фазовая скорость
волны равна
.
Фазовая скорость
волны равна
![]() ,
тогда
,
тогда 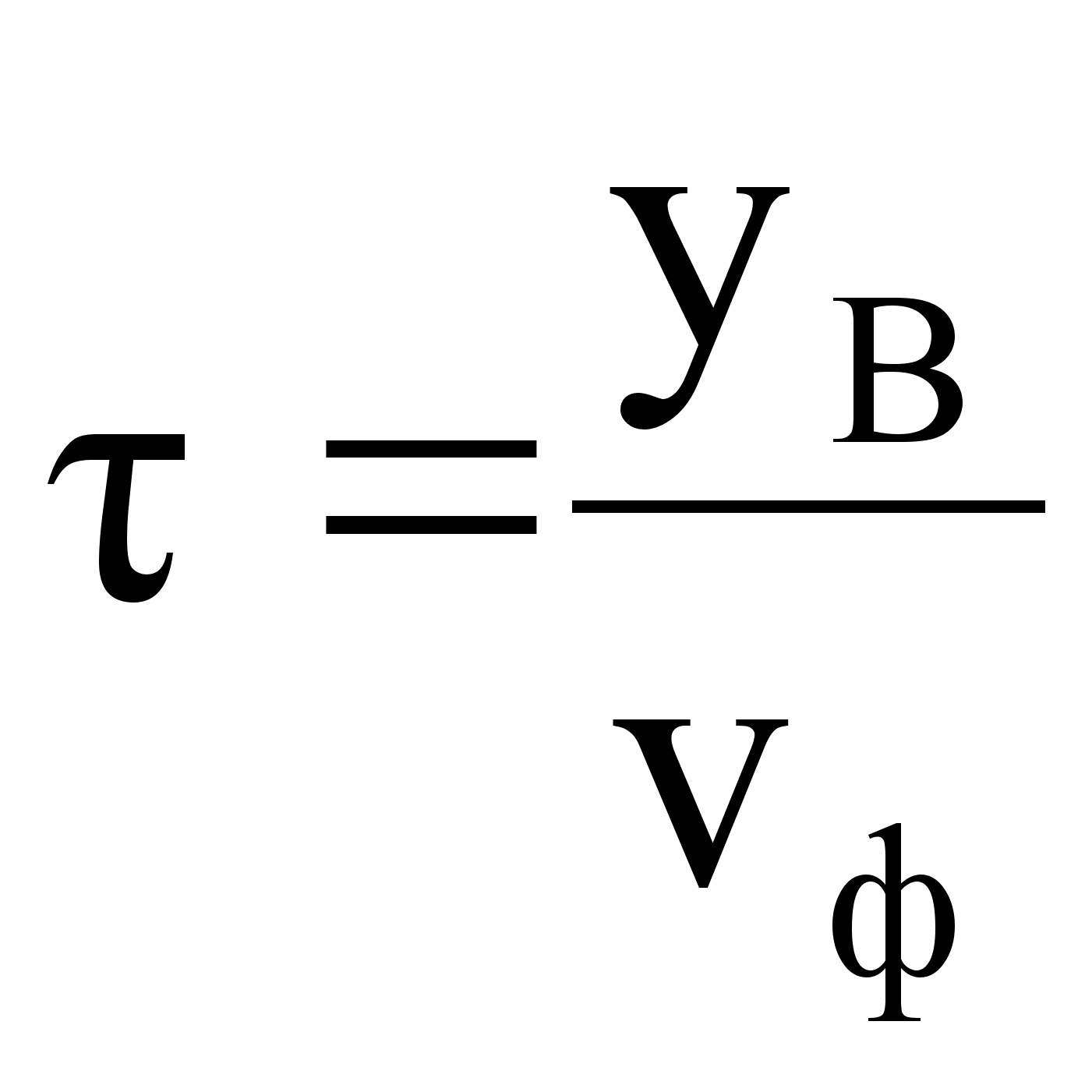 .
Учитывая соотношения
для
.
Учитывая соотношения
для ![]() и
и ![]() и формулы
и формулы ![]() и
и
![]() ,
можно записать
уравнение
колебаний точки
В в разных видах:
,
можно записать
уравнение
колебаний точки
В в разных видах:
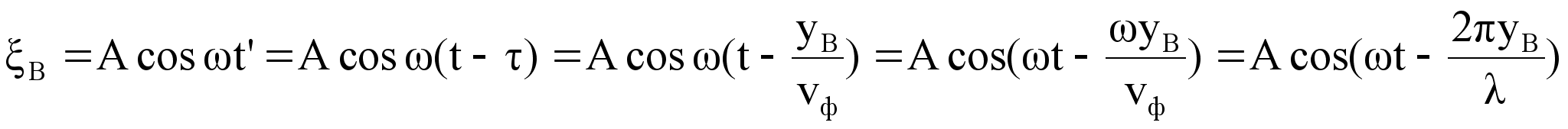 .
.
Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:
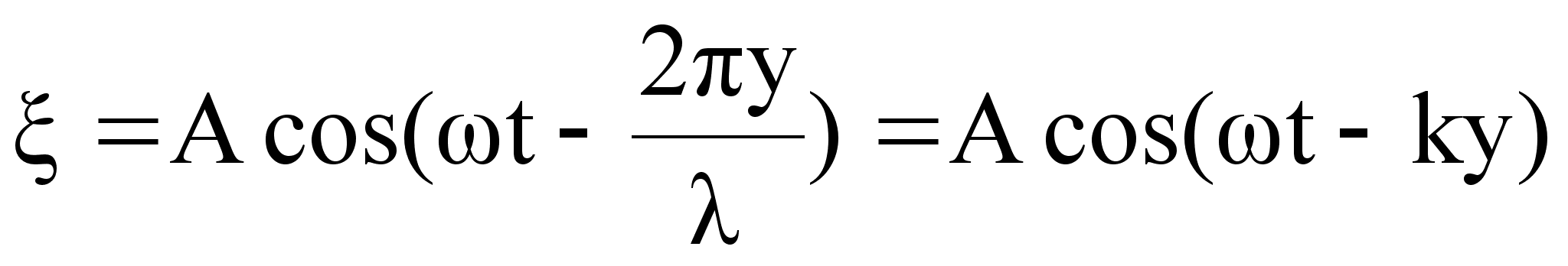 ,
,
где 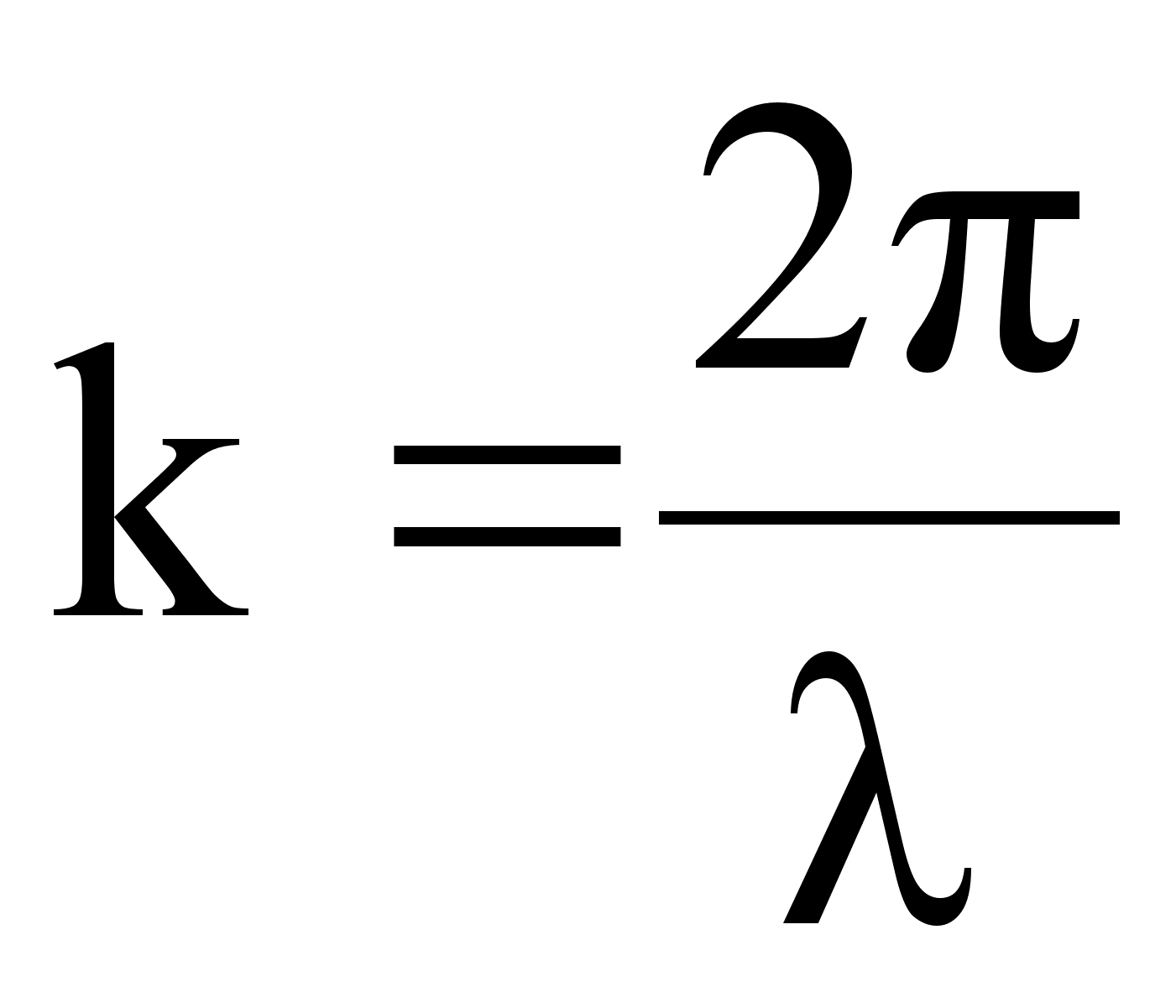 - волновое число
(см. определение
выше).
- волновое число
(см. определение
выше).
Это уравнение
и есть уравнение
для смещения
![]() любой точки
пространства
в любой момент
времени, т.е.
уравнение
бегущей волны, где А – амплитуда,
величина
любой точки
пространства
в любой момент
времени, т.е.
уравнение
бегущей волны, где А – амплитуда,
величина  - фаза волны,
которая в отличии
от фазы колебаний
зависит и от времени
«t», и
от расстояния
«y» колеблющейся
точки от источника
колебаний.
- фаза волны,
которая в отличии
от фазы колебаний
зависит и от времени
«t», и
от расстояния
«y» колеблющейся
точки от источника
колебаний.
Вернемся к разделению волн по форме фронта волны и к понятию луча, как направления распространения колебательного процесса. Учтем, что в изотропной среде лучи перпендикулярны фронту и имеют вид прямых линий. Тогда уравнение бегущей волны, полученное выше, есть уравнение плоской бегущей волны, т.е. когда фронт волны – плоскость.
Уравнение плоской отраженной волны в одномерном пространстве легко получить, если представить ее как бегущую волну в отрицательном направлении оси ОУ, что приведет к замене в уравнении бегущей волны координаты «y» на «-y»:
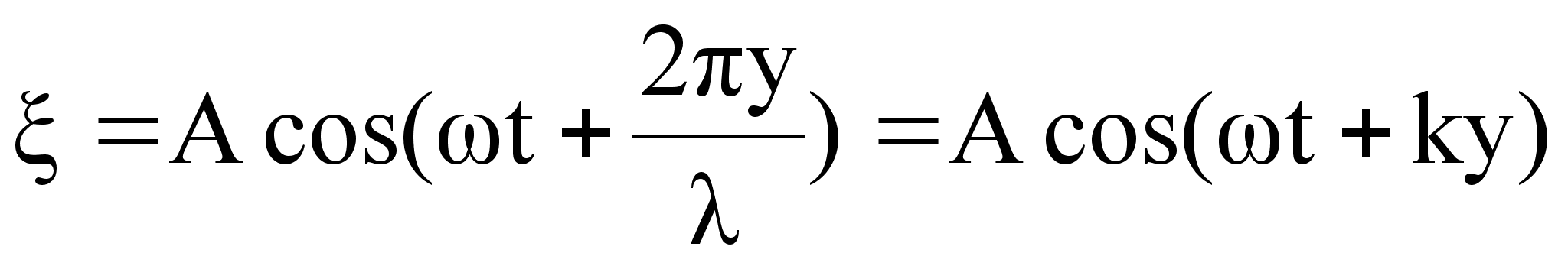 .
.
Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.
Похожие работы
... поступления 5 мая 1980 г.; // http://www.sciteclibrary.ru/- rus/catalog/pages/4797.html . Для подготовки данной работы были использованы материалы с сайта http://referat.ru О псевдоволнах электромагнитного поля В.В. Сидоренков МГТУ им. Н.Э. Баумана Общепринятая логика обсуждения вопроса о переносе энергии электромагнитного поля посредством волн такова, что проблемы здесь как бы и нет: всем все ...
... выше, это невозможно в принципе, поскольку, согласно уравнениям Максвелла (1), ЭМ волн с такими характеристиками в Природе нет. Итак, проблема с выяснением физического механизма переноса энергии волнами ЭМ поля объективно существует, и для ее разрешения требуется, по всей видимости, весьма нестандартный эвристический подход. Однако в наличии у нас имеется только система уравнений электродинамики ...
... и не возникает вихревое электрическое. «... по закону электромагнитной индукции переменное магнитное поле всегда порождает вихревое электрическое ...» Энциклопедия элементарной физики. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ. Таким образом, электрическая напряженность поля в виде вихревого электрического потока возникает не от движения магнита, а от изменения в пространстве магнитного потока, например, вокруг ...
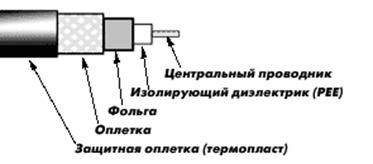
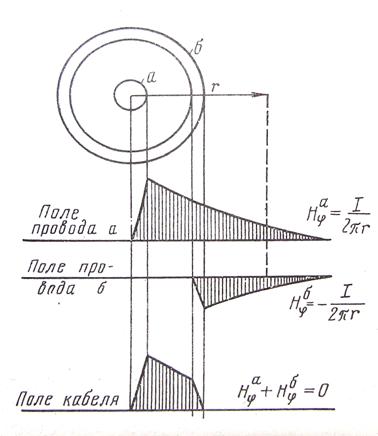
... применяются не только в метровом, дециметровом и сантиметровом диапазоне волн, но и на длинных, средних и коротких волнах радиовещательного диапазона, а также во многих низкочастотных устройствах систем автоматики и телемеханики. 8. Расчет основных параметров коаксиального кабеля марки РК‑50–3–11 Каждому кабелю присвоено условное обозначение, которое включает буквы, обозначающие марку ...
0 комментариев