Навигация
6. Волновое уравнение.
Когда мы рассматривали колебания, то для любой колебательной системы получали дифференциальное уравнение, для которого соответствующее уравнение колебаний являлось решением. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:
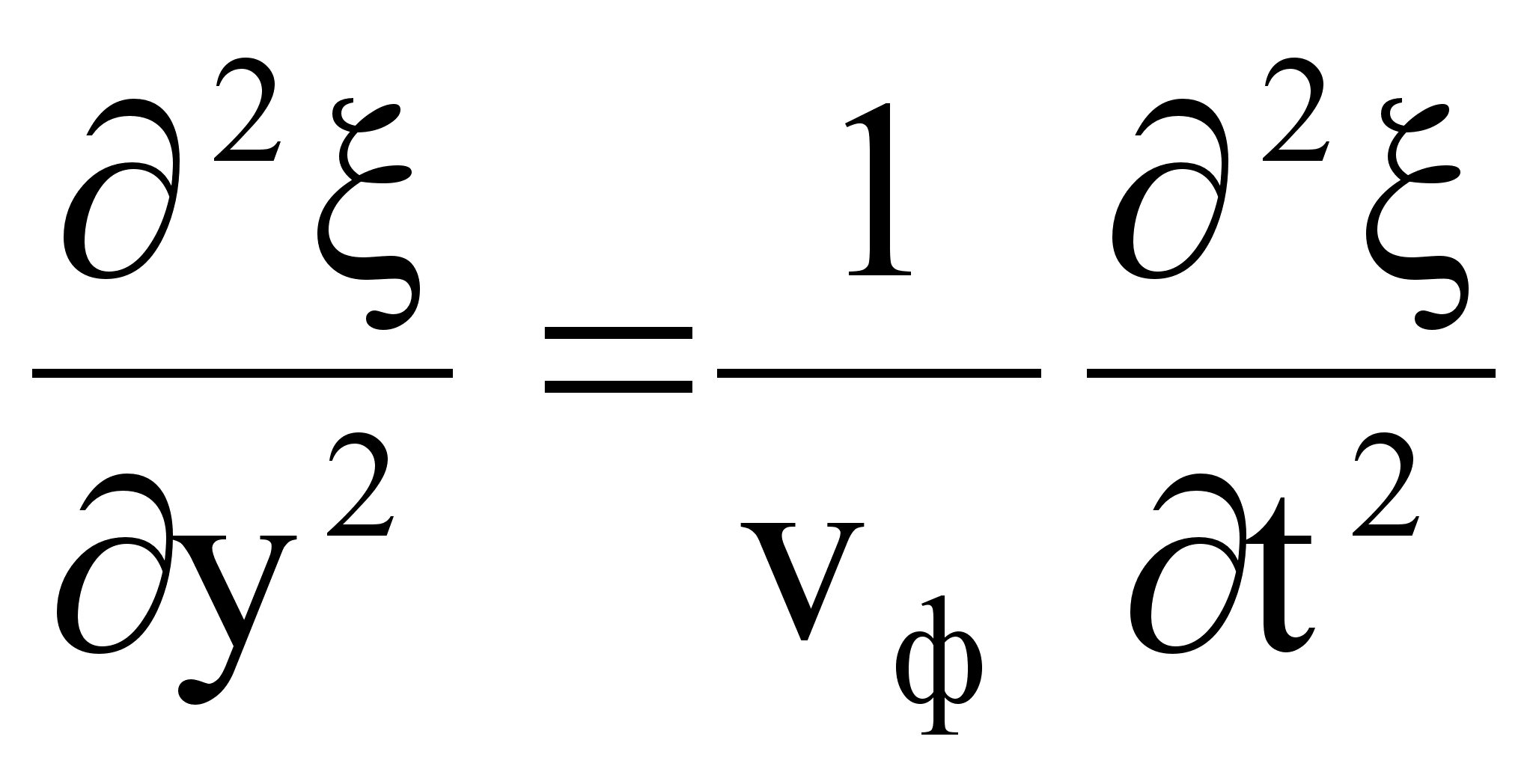 ,
,
где
![]() - фазовая скорость
волны.
- фазовая скорость
волны.
Уравнения
бегущей и отраженной
волн и волновое
уравнение
представлены
для случая
одного измерения,
т.е. распространения
волны вдоль
оси ОУ. В волновое
уравнение
входят вторые
частные производные
по времени и координате
от смещения
потому, что ![]() есть функция
двух переменных
t и y.
есть функция
двух переменных
t и y.
7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды.
Если смещение любой точки среды с координатой y в момент времени t задано уравнением:
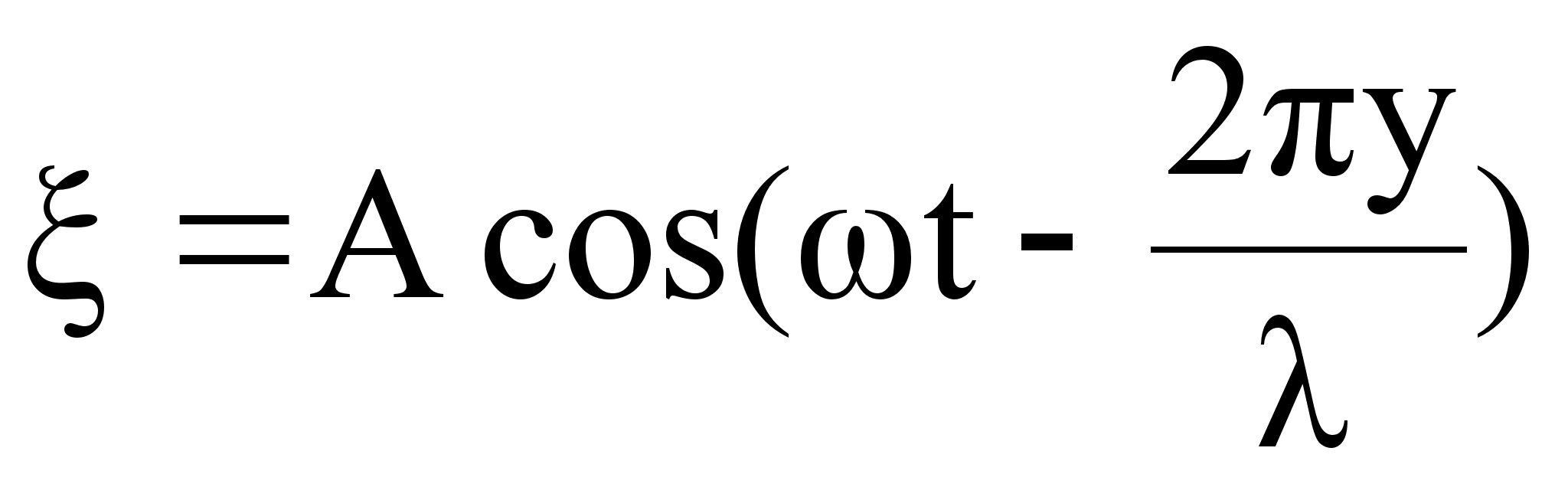 ,
,
то скорость
этой точки
есть величина
 ,
а ускорение
-
,
а ускорение
-  :
:
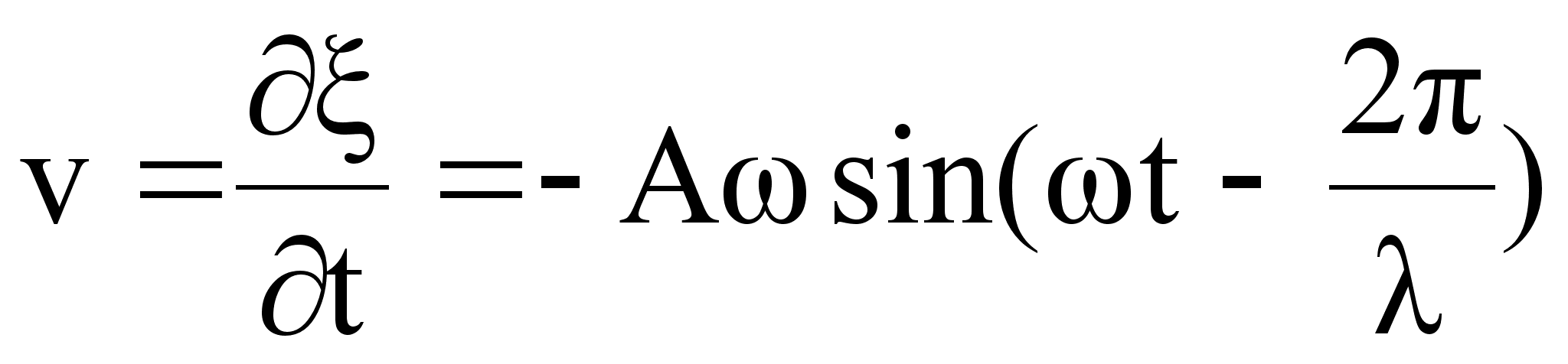 ,
,
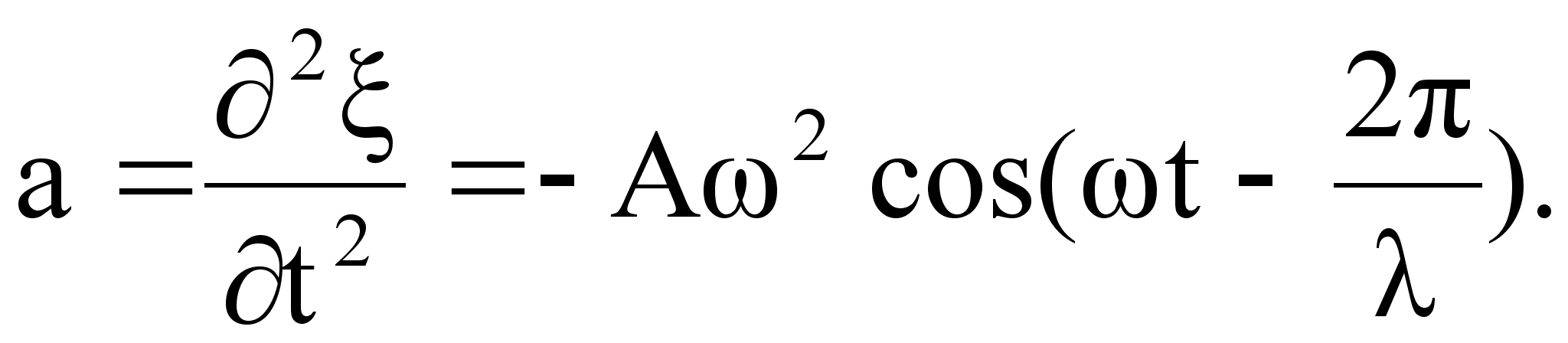
В
среде распространяется
плоская упругая
волна и переносит
энергию, величина
которой в объеме
![]() равна:
равна:
 ,
,
где ![]() -
объемная плотность
среды.
-
объемная плотность
среды.
Если выбранный
объем записать
как ![]() ,
где S – площадь
его поперечного
сечения, а
,
где S – площадь
его поперечного
сечения, а ![]() - его длина, то
среднее количество
энергии, переносимое
волной за единицу
времени через
поперечное
сечение S,
называется
потоком
- его длина, то
среднее количество
энергии, переносимое
волной за единицу
времени через
поперечное
сечение S,
называется
потоком ![]() через его
поверхность:
через его
поверхность:
![]()
 .
.
Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.
Эта величина определяется соотношением:
![]() ,
,
где  -объемная плотность
энергии волны,
-объемная плотность
энергии волны,
![]() - фазовая скорость
волны. Так как
фазовая скорость
волны
- фазовая скорость
волны. Так как
фазовая скорость
волны ![]() - вектор, направление
которого совпадает
с направлением
распространения
волны, то можно
величине плотности
потока энергии
I придать
смысл векторной
величины:
- вектор, направление
которого совпадает
с направлением
распространения
волны, то можно
величине плотности
потока энергии
I придать
смысл векторной
величины:
![]() .
.
Величина ![]() , вектор плотности
энергии волны,
впервые была
введена Н.А.
Умовым в 1984 году
и получила
название вектора
Умова. Подобная
величина для
электромагнитных
волн называется
вектором Умова
- Пойнтинга.
, вектор плотности
энергии волны,
впервые была
введена Н.А.
Умовым в 1984 году
и получила
название вектора
Умова. Подобная
величина для
электромагнитных
волн называется
вектором Умова
- Пойнтинга.
Интенсивностью
волны называется
модуль среднего
значения вектора
Умова
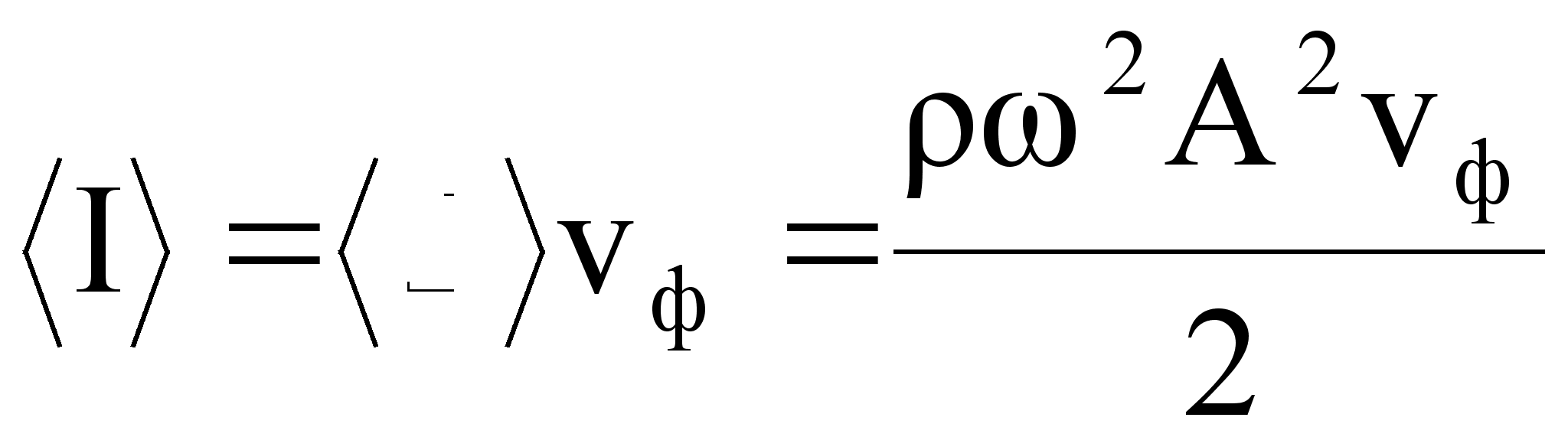 .
.
§ 1.4. Принцип суперпозиции волн. Групповая скорость.
Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.
Согласно принципу
суперпозиции
накладываться
друг на друга
без взаимного
искажения могут
волны любой
формы. В результате
наложения волн
результирующее
колебание
каждой частицы
среды может
происходить
по любому сложному
закону. Такое
образование
волн называется
волновым пакетом.
Скорость
движения волнового
пакета не совпадает со скоростью
ни с одной из
слагаемых волн.
В этом случае
говорят о скорости
![]() волнового
пакета. Скорость
перемещения
максимума
группы волн
(волнового
пакета) называется
групповой
скоростью.
Она равна скорости
переноса энергии
волнового
пакета.
волнового
пакета. Скорость
перемещения
максимума
группы волн
(волнового
пакета) называется
групповой
скоростью.
Она равна скорости
переноса энергии
волнового
пакета.
На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.
В общем виде связь между групповой и фазовой скоростями имеет вид:
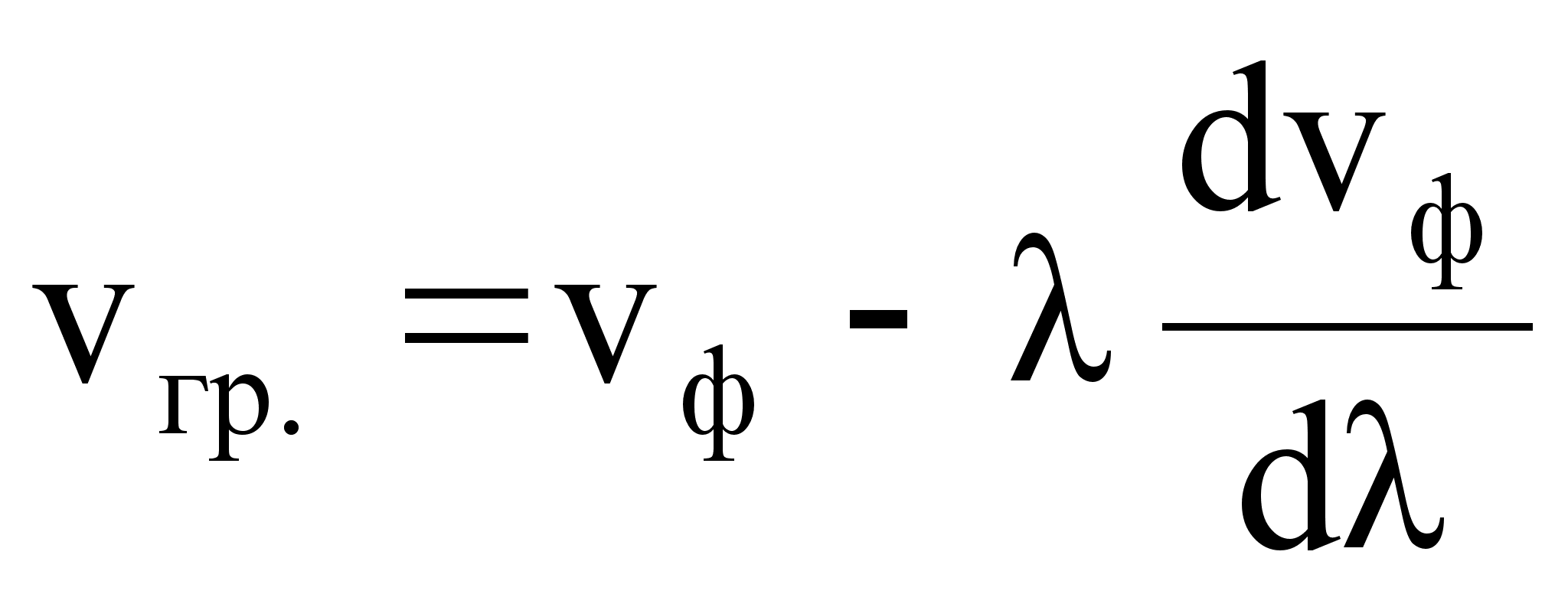 .
.
1. Интерференцией волн называется явление наложение двух и более волн, при котором в зависимости от соотношения между фазами этих волн происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других.
В пространстве
всегда найдутся
такие точки,
в которых разность
фаз складываемых
колебаний равна величине
![]() ,
где k – целое
число, т.е. волны
(от разных
источников)
приходят в
такие точки
в фазе. В них
будет наблюдаться
устойчивое,
неизменно
продолжающееся
все время усиление
колебаний
частиц. Найдутся
в пространстве,
где распространяется
несколько волн,
и такие точки,
где разность
фаз будет равна
,
где k – целое
число, т.е. волны
(от разных
источников)
приходят в
такие точки
в фазе. В них
будет наблюдаться
устойчивое,
неизменно
продолжающееся
все время усиление
колебаний
частиц. Найдутся
в пространстве,
где распространяется
несколько волн,
и такие точки,
где разность
фаз будет равна
![]() ,
т.е. волны приходят
в эти точки в
противофазе.
В таких точках
пространства
будет наблюдаться
устойчивое
ослабление
колебаний
частиц.
,
т.е. волны приходят
в эти точки в
противофазе.
В таких точках
пространства
будет наблюдаться
устойчивое
ослабление
колебаний
частиц.
Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую частоту, постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям и источники, создающие такие волны, называются когерентными. Плоские синусоидальные волны, частоты которых одинаковы, когерентны всегда.
2. Запишем условия
максимумов
и минимумов
при интерференции.
Когерентные
точечные источники ![]() и
и ![]() испускают
волны по всем
направлениям. До точки наблюдения
М расстояние
от первого
источника
испускают
волны по всем
направлениям. До точки наблюдения
М расстояние
от первого
источника ![]() ,
а от второго
-
,
а от второго
- ![]() .
.
Колебания точки
М под действием
волн от двух
источников![]() и
и ![]() описываются
уравнениями:
описываются
уравнениями:
 ,
,  .
.
Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел «Сложение колебаний»):
 .
.
Амплитуда
колебаний точки
М максимальна
(![]() ),
если
),
если
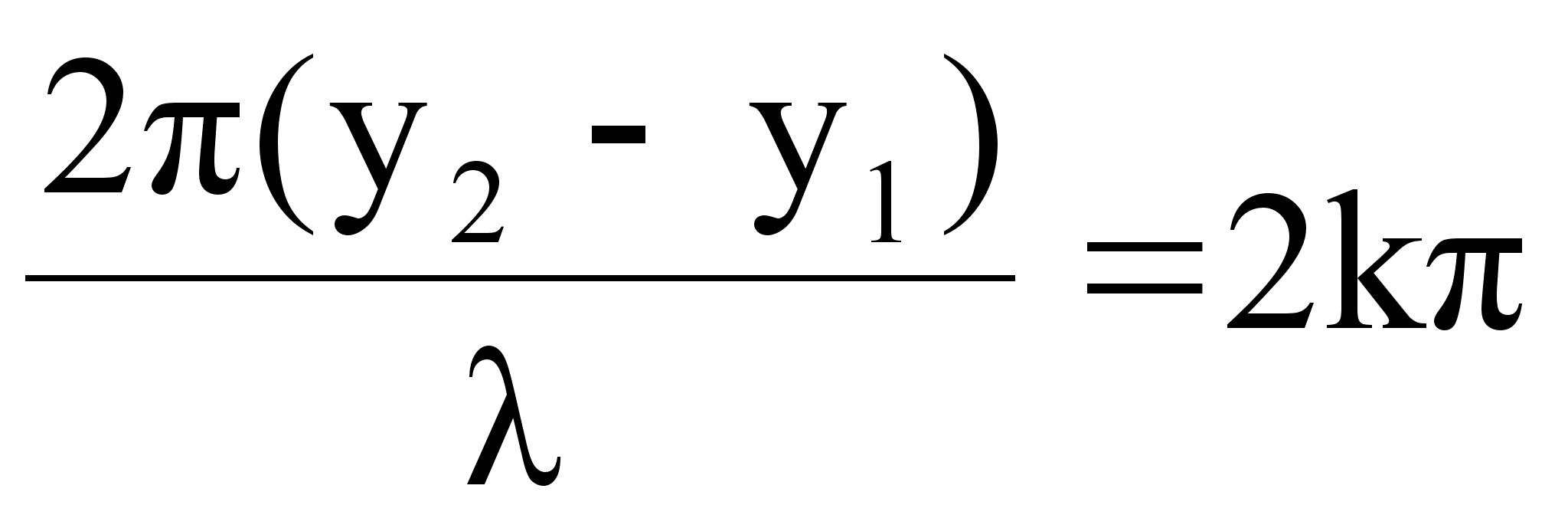 , где
, где ![]()
Величина
![]() называется
разностью
хода двух волн.
называется
разностью
хода двух волн.
Условие максимума при интерференции имеет вид:
![]() .
.
Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум.
Амплитуда
колебаний точки
М минимальна
(![]() ),
если
),
если
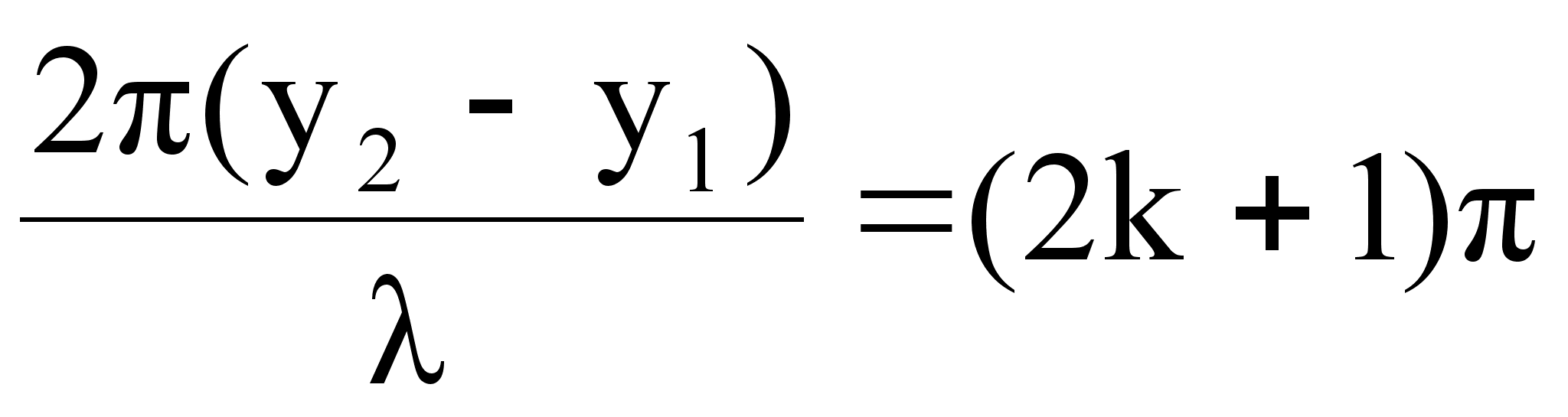 , (
, (![]() ).
).
Условие минимума при интерференции имеет вид:
![]() .
.
Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум.
3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид:
 ,
, 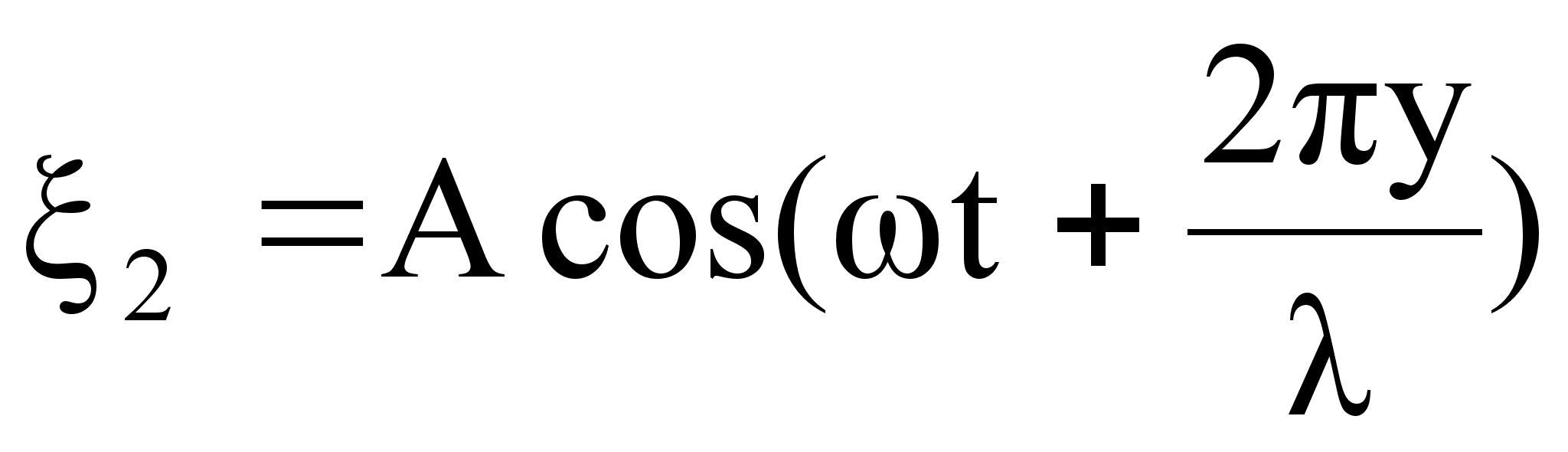
Суммарное
смещение ![]() частицы среды,
находящейся
на расстоянии y от источника
колебаний,
равно сумме
смещений
частицы среды,
находящейся
на расстоянии y от источника
колебаний,
равно сумме
смещений ![]() и
и ![]() :
:
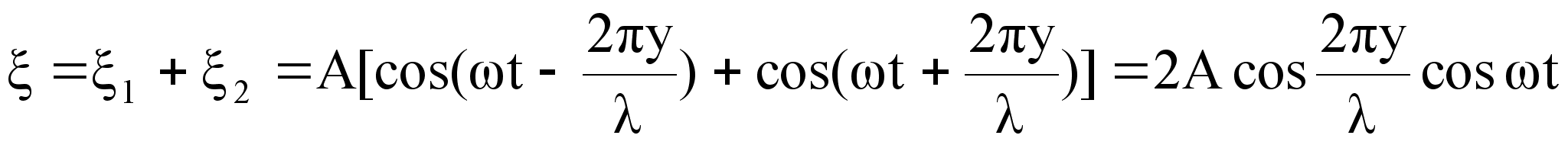 .
.
Это и есть уравнение
стоячей волны.
Величина 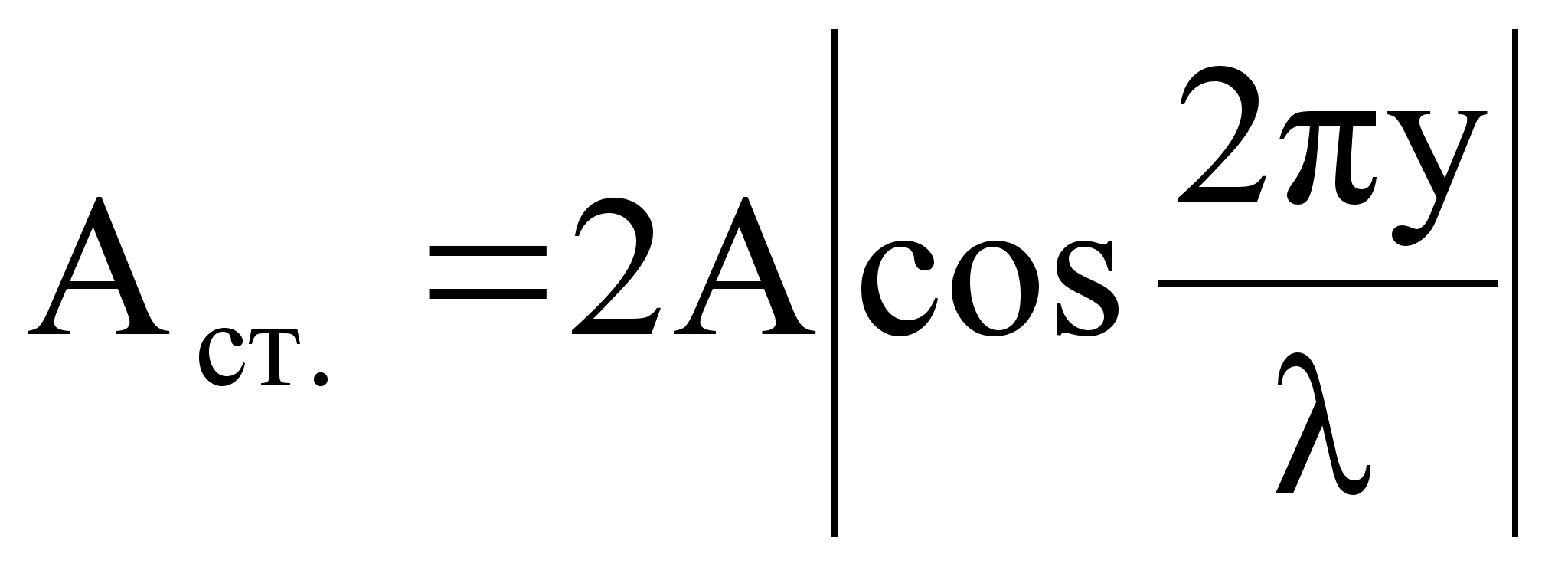 - амплитуда, а
(
- амплитуда, а
(![]() )
- фаза стоячей
волны. Можно
сказать, что
частицы в стоячей
волне имеют
одну фазу колебаний.
Амплитуда
колебаний
частиц в стоячей
волне зависит
от их координат
(расстояний
до источника
колебаний), но
не зависит от
времени. Знак
модуля поставлен
в формуле для
амплитуды
стоячей волны,
потому что
амплитуда –
величина
положительная.
)
- фаза стоячей
волны. Можно
сказать, что
частицы в стоячей
волне имеют
одну фазу колебаний.
Амплитуда
колебаний
частиц в стоячей
волне зависит
от их координат
(расстояний
до источника
колебаний), но
не зависит от
времени. Знак
модуля поставлен
в формуле для
амплитуды
стоячей волны,
потому что
амплитуда –
величина
положительная.
В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения, их положение определяется из условия:
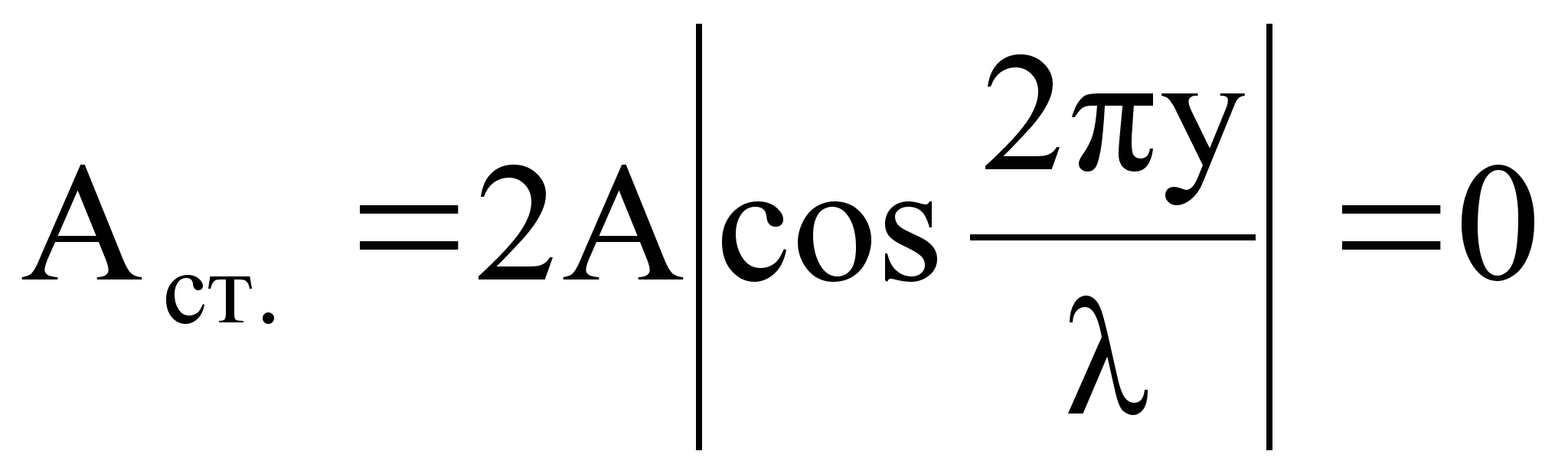 ,
отсюда следует
,
отсюда следует
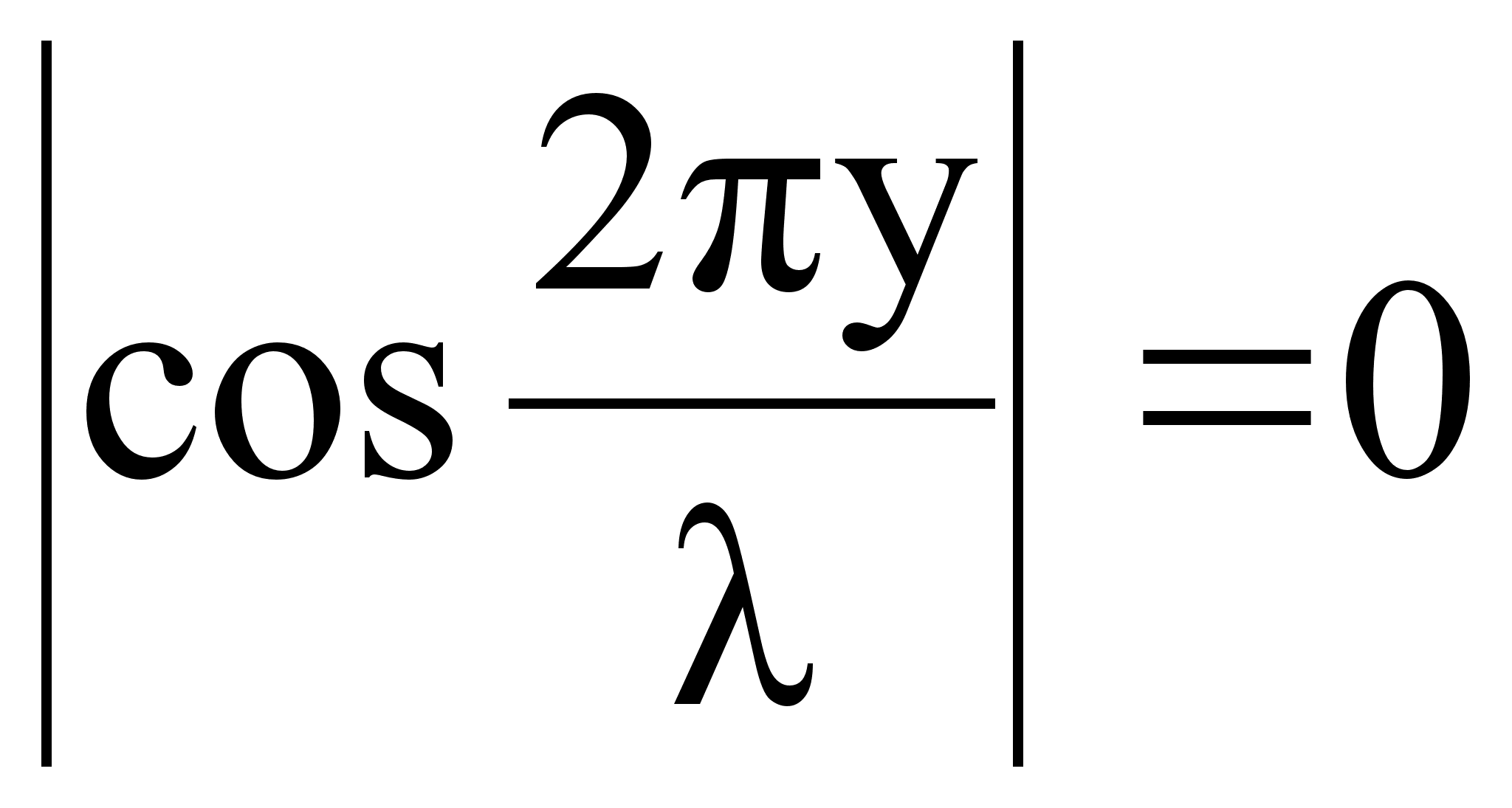 . Выполнение
этого соотношения будет при условии
. Выполнение
этого соотношения будет при условии
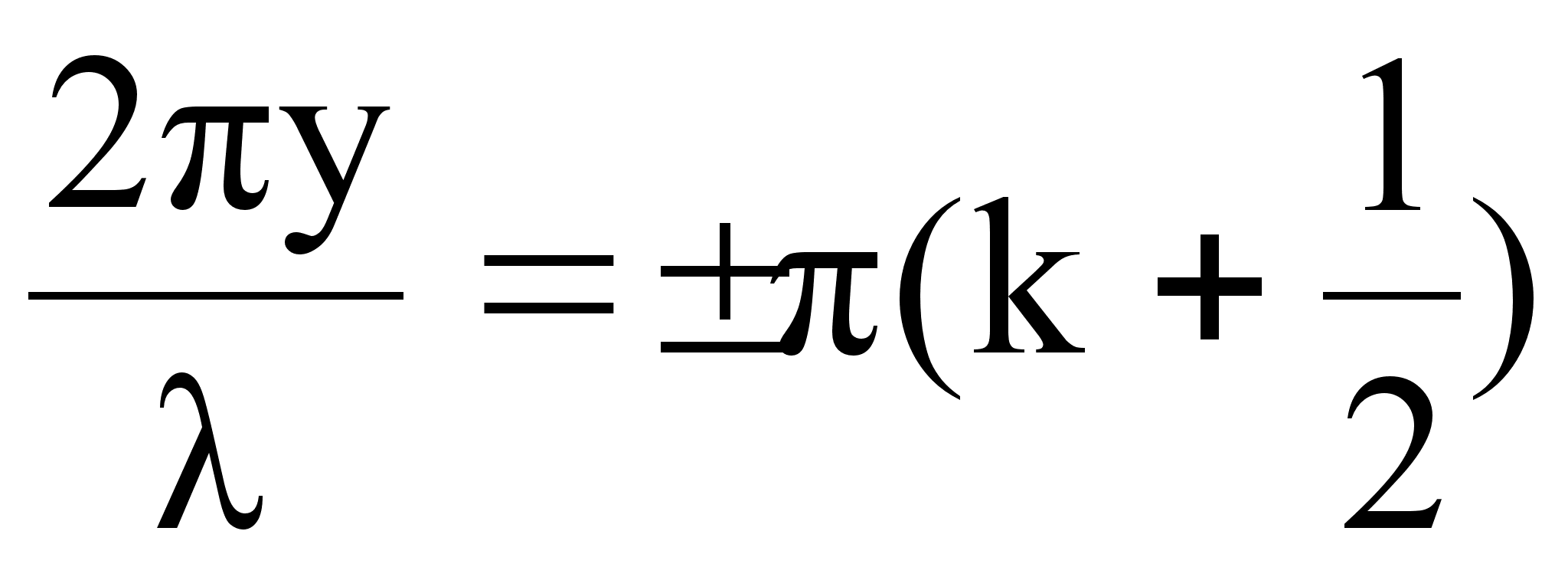 для
для ![]() Итак, координаты
узлов задаются
формулой:
Итак, координаты
узлов задаются
формулой:
![]() .
.
Расстояние
между двумя
соседними
узлами равно
![]() .
.
Точки среды, колеблющиеся с наибольшей амплитудой, называются пучностями стоячей волны, их положение (координаты) определяются соотношением:
![]() .
.
Это уравнение можно получить из условия максимума амплитуды
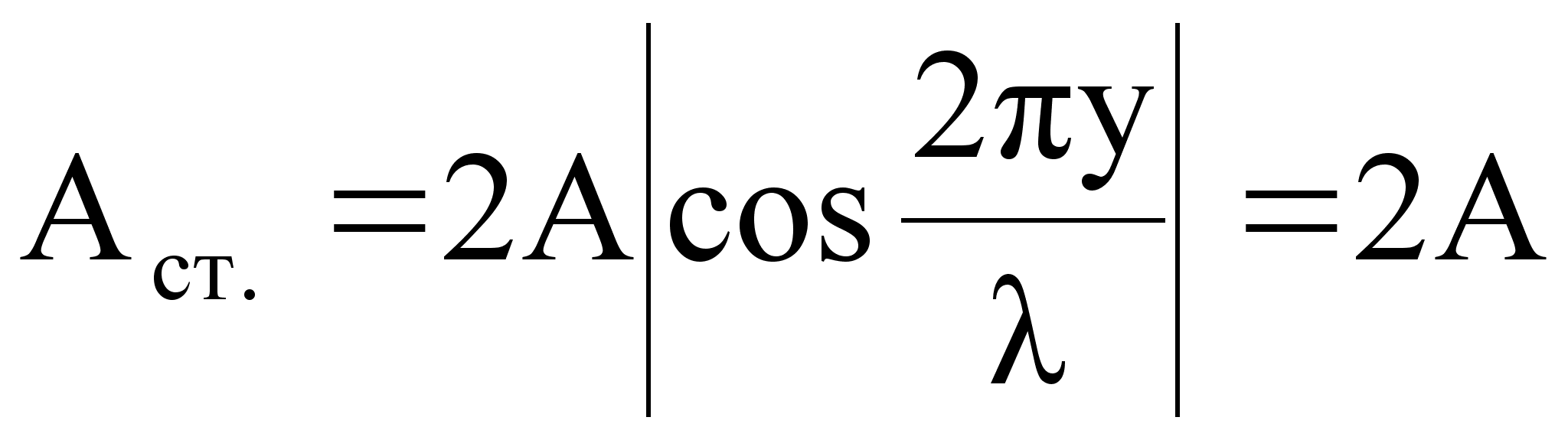 , т.е.
, т.е.  .
Последнее
соотношение
выполняется
при значениях
аргумента
.
Последнее
соотношение
выполняется
при значениях
аргумента 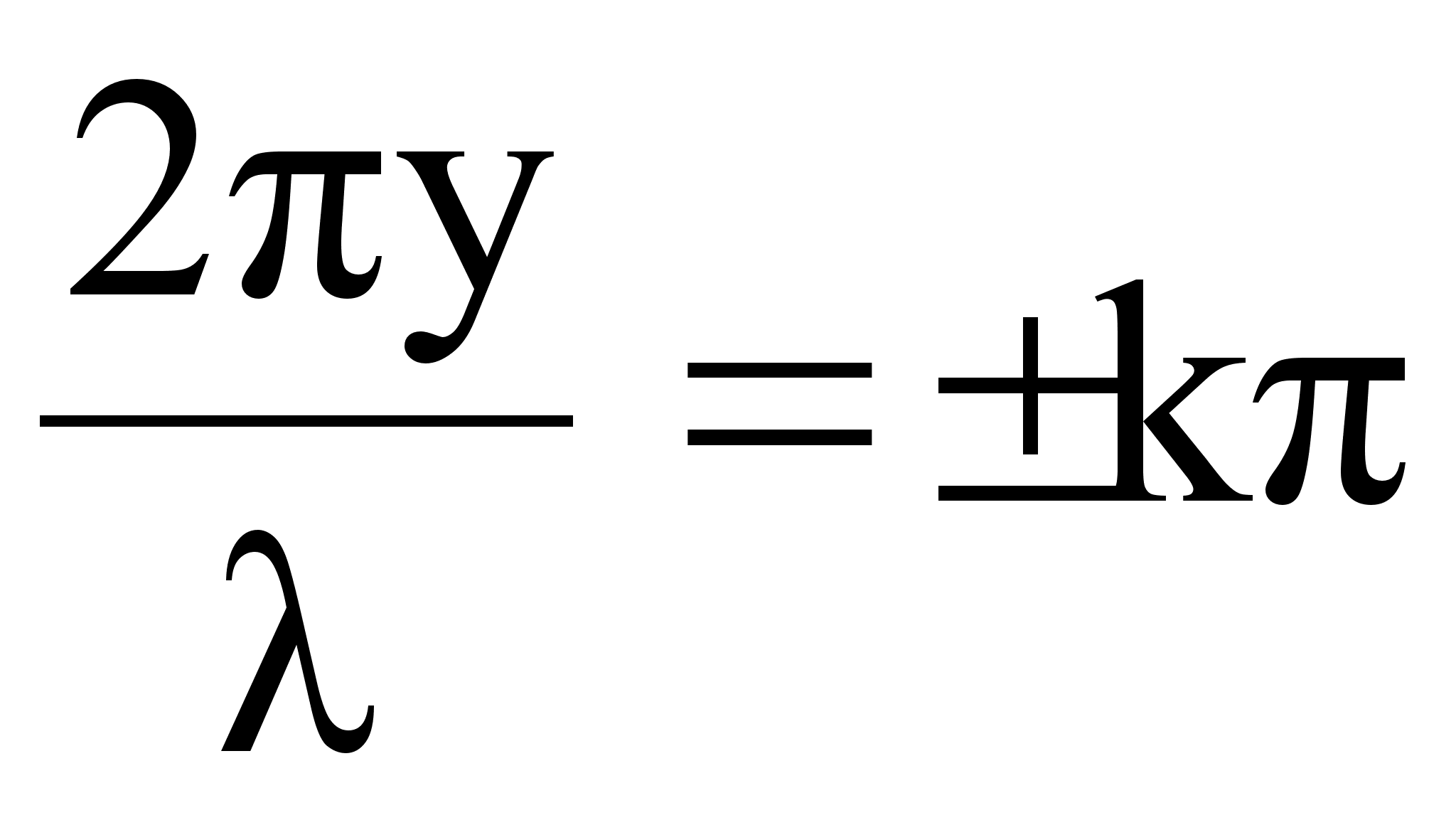 (
(![]() ).
).
Расстояние
между двумя
соседними
пучностями
равно ![]() .
.
Похожие работы
... поступления 5 мая 1980 г.; // http://www.sciteclibrary.ru/- rus/catalog/pages/4797.html . Для подготовки данной работы были использованы материалы с сайта http://referat.ru О псевдоволнах электромагнитного поля В.В. Сидоренков МГТУ им. Н.Э. Баумана Общепринятая логика обсуждения вопроса о переносе энергии электромагнитного поля посредством волн такова, что проблемы здесь как бы и нет: всем все ...
... выше, это невозможно в принципе, поскольку, согласно уравнениям Максвелла (1), ЭМ волн с такими характеристиками в Природе нет. Итак, проблема с выяснением физического механизма переноса энергии волнами ЭМ поля объективно существует, и для ее разрешения требуется, по всей видимости, весьма нестандартный эвристический подход. Однако в наличии у нас имеется только система уравнений электродинамики ...
... и не возникает вихревое электрическое. «... по закону электромагнитной индукции переменное магнитное поле всегда порождает вихревое электрическое ...» Энциклопедия элементарной физики. ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ. Таким образом, электрическая напряженность поля в виде вихревого электрического потока возникает не от движения магнита, а от изменения в пространстве магнитного потока, например, вокруг ...
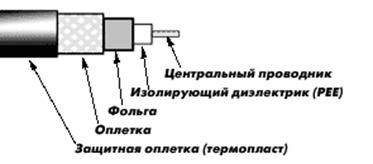
... применяются не только в метровом, дециметровом и сантиметровом диапазоне волн, но и на длинных, средних и коротких волнах радиовещательного диапазона, а также во многих низкочастотных устройствах систем автоматики и телемеханики. 8. Расчет основных параметров коаксиального кабеля марки РК‑50–3–11 Каждому кабелю присвоено условное обозначение, которое включает буквы, обозначающие марку ...
0 комментариев