Навигация
Минимизация стоимостей перевозок
Московский Государственный Колледж
Информационных Технологий
Курсовой проект
по предмету
« Языки программирования и разработка
программного обеспечения »
на тему :
« Минимизация стоимостей перевозок »
Работу выполнил Работу проверили
студент группы П-407 Преподаватели
Чубаков А.С. Капустина Р.Н.
Токарев С.Б.
1998 г.
КР. 2203 81 - 21
ВВЕДЕНИЕ
Развитие современного общества характеризуется повышением технического
уровня , усложнением организационной структуры производства , углублением общественного разделения труда , предъявлением высоких требований к методам планирования и хозяйственного руководства. В этих условиях только научный подход к руководству к экономической жизни общества позволит обеспечить высокие темпы развития народного хозяйства. В настоящие время новейшие достижения математики и современной вычислительной техники находят все более широкие применение в экономических исследованиях и планированияx. Этому способствует развитие таких разделов математики . как математическое программирование , теория игр , теория массового обслуживания , а так же бурное развитие быстродействующей электронно - вычислительной техники. Одной из основных ставится задача создания единой системы оптимального планирования и управление народным хозяйством на базе широкого применения математических методов в электронно - вычислительной техники в экономике.
Решение экстремальных экономических задач можно разбить на три этапа :
Построение экономико - математической задачи.
Нахождение оптимального решения одним из математических методов.
Промышленное внедрение в народное хозяйство.
Построение экономическо - математической модели состоит в создании упрощенной математической модели , в которой в схематичной форме отражена структура изучаемого процесса. При этом особое внимание должно быть уделено отражении в модели всех существенных особенностей задачи и учет всех ограничивающих
условий , которые могут повлиять на результат. Затем определяется цель решения , выбирается критерий оптимальности и дают математическую формулировку задачи.
Составными частями математического программирования являются линейное , нелинейное и динамическое программирование. При исследовании в большинстве случаев имеют место задачи нелинейного программирования , аппроксимация их линейными задачами вызвана только тем , что последние хорошо изучены.
Динамическое программирование как самостоятельная дисциплина сформулировалась в пятидесятых годах нашего века. Большой вклад в ее развитие внес американский математик Р. Бельман. Дальнейшие развитие динамическое программирование получило
в трудах зарубежных ученых Робертса , Ланга и др.
В настоящие время оно в основном развивается в планировании приложений к различным родам многоэтапным процессам.
КР. 2203 81 – 21
2. ЭКОНОМИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Производственное предприятие имеет в своем составе три филиала которые производят однородную продукцию
соответственно в количествах , равных 50 , 30 и 10 единиц. Эту продукцию получают четыре потребителя , расположенных в разных
местах. Их потребности соответственны равны 30 , 30 , 10 и 20 единиц. Тарифы перевозов единицы продукции от каждого филиалов соответствующим потребителям задаются матрицей :
1 2 4 1
Сij = 2 3 1 5
3 2 4 4
Составить такой план прикрепления получателе продукции к ее поставщикам , при котором общая стоимость перевозок будет минимальной.
КП. 2203 81 - 21
2.МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
2. Математическая модель задачи
Имеется:
m (i=1,2,…,m) – филиалы.
Ai – количество единиц продукции «i» филиала.
n (j=1,2,…,n) – потребители
Bj – потребности «j» потребителя
Cij – стоимость перевозки 1 условной единицы продукции
от «i» филиала к «j» потребителю
Ограничения:
Балансовое ограничение.
![]() Предполагается,
что сумма всех
запасов (ai) равна
сумме всех
заявок (bj):
Предполагается,
что сумма всех
запасов (ai) равна
сумме всех
заявок (bj):
![]()
2. Ресурсное ограничение.
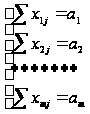
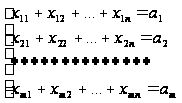
Суммарное количество груза, направленного из каждого пункта отправления во все пункты назначения должно быть равно запасу груза в данном пункте. Это даст m – условий равенств:
или
![]()
![]()
Похожие работы
... так далее чередуясь. Берется минимальное по абсолютной величине значение в отрицательных клетках. Во всех отрицательных клетках это значение отнимается, в положительных прибавляется. Получили новый план перевозок. Решение задачи 1. Определим модель задачи b1+b2+b3+b4+b5+b6=230+220+130+170+190+110=1050 a1+a2+a3+a4+a5=240+360+180+120+150=1050 Так как Σai=Σbj, то модель задачи ...
... четырех-, шести-,восьмиосных вагонов, участвующих в перевозках; — техническая норма загрузки четырех-, шести-, восьмиосных вагонов данным грузом. 1.4 Рационализация перевозок грузов различными видами транспорта Факторы, определяющие развитие и размещение транспортной системы Капитальные вложения, направляемые на развитие транспорта Размещение отраслей промышленности и сельского ...
... : - каждому виду продукции должна соответствовать одна транспортная матрица; - все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции. 3.2 Решение транспортной задачи на примере ООО «Дубровчанка+» Применяя теорию транспортной задачи к показателям работы ООО «Дубровчанка +», составим следующую транспортную ...
... бумажными технологиями). Третий этап. Внедрение самостоятельного электронного документооборота. Организация работы арендуемых приложений.4.3 Создание Информационно-логистического центра транспортного комплекса калининградского региона 4.3.1 Организационная модель ИЛЦ 4.3.1.1 Закрытое акционерное общество "Информационно-логистический Центр" Акционерная компания ( ...

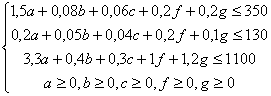
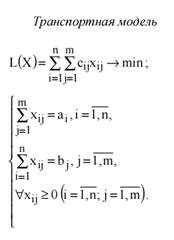
0 комментариев