Общие вопросы проектирования
Разработка формирователей логических уровней (ФЛУ)
Выбор типа компаратора
Определение мощности и тока, потребляемых ФЛУ
Разработка принципиальной схемы автомата
Разработка схемы установки счетчика в исходное (нулевое) состояние
Проектирование схемы индикации в десятичной форме
Разработка принципиальной схемы индикации
Выбор схемы выпрямления и типа диодов
Навигация
Определение мощности и тока, потребляемых ФЛУ
Электронное устройство счета и сортировки
43356
знаков
11
таблиц
17
изображений
2.4. Определение мощности и тока, потребляемых ФЛУ.
Рассчитаем рассеиваемую мощность резисторов на примере формирователя логического уровня для первого датчика:
(25.) 
, 
, 
,
(26.) 
, 
, 
.
где: 
, 
, 
, 
, 
, 
- расчетные значения рассеиваемых мощностей.
– уточненное значение тока делителя после выбора резисторов по ГОСТ.
,
,
,
,
.
Номинальное значение рассеиваемой мощности PHR должно быть не менее расчетной:
(27.) 
Аналогично просчитав мощности резисторов делителей датчиков Д2 – Д3, определим суммарное потребление мощности резистивных делителей датчиков:
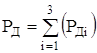
Ток потребления одного корпуса микросхемы компаратора равен 3,6 мА, в нашем случае 3 корпуса. Мощность потребления микросхемы выполняющую функцию 3И–НЕ (К564ЛА9) равна 20 мВт на каждый логический элемент. Общая потребляемая мощность ФЛУ будет равен сумме всех обозначенных ниже мощностей:
(28.) 
Где:
– ток потребляемый микросхемой от двухполярного питания.
3. Проектирование цифрового автомата.
3.1. Минимизация логической функции автомата.
Задачи в цифровой технике, как правило, формируются в виде таблиц истинности. Решение задачи сводится к нахождению аналитического выражения логической функции, которое соответствовало бы этой таблице. В данной задаче программа сортировки заданна следующей таблицей истинности:
Таблица 6.Программа сортировки.
| Номер набора | Х1 | Х2 | Х3 | Y |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 0 | 1 | 1 | 1 |
| 4 | 1 | 0 | 0 | 1 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 1 | 1 | 0 | 1 |
| 7 | 1 | 1 | 1 | 0 |
В таблице истинности выделим строки, в которых выходная переменная Y принимает значение 1. Для каждой строки таблицы составляем конъюнктивный терм (контерм) – логическое умножение всех входных переменных. Причем записывают сомножитель в прямом виде – Xi, если рассматриваемая переменная равна “1”, в противном случае записывают в инверсном виде – 
i.. Таким образом составляем столько выражений, сколько имеется строк с Y=1;
Записывая логическую сумму всех найденных контермов, получаем искомую функцию в дизъюнктивной форме.
В соответствии с таблицей истинности (таблица 6) в строках 3, 4, 6 функция Y=1. Контермы для каждой из строк имеют следующий вид:
а) строка 3 – 
;
б) строка 4 – 
;
в) строка 6 – 
.
Искомая функция записывается в виде логической суммы конъюнктивных термов:
(29.) 
или
(30.) 
Преобразуем выражение (30) по правилам алгебры логики. В соответствии с дистрибутивным законом:
(31.) 
.
Логическая схема, построенная по выражению (31), приведена на рисунке 6.
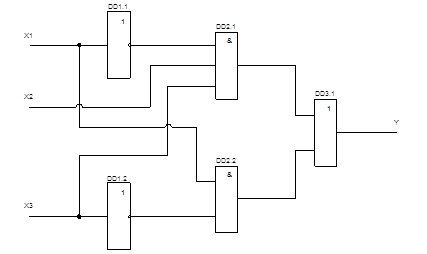
Рисунок 6.Схема функциональная логического устройства.
Похожие работы
... все названные критерии. Причем данным набором дело не ограничивается, поскольку наука и практика не стоит на месте, появляются новые реалии и обстоятельства. 2.2.Проблема выбора система электронного документооборота на предприятиях малого и среднего бизнеса Основными российскими тенденциями начала третьего тысячелетия стал безбумажный технологический бум во всех сферах человеческой ...
... устойчивыми банками; · использовать надежный механизм защиты информации, основанный на проверенных криптографических стандартах; · оставаться дешевой для Internet-торговцев и покупателей. 7. Банки и электронные деньги Политика содержания отделений, с их большими расходами и низкой рентабельностью, обязательно окажется под угрозой там, где еще не оказалась. Небольшой американский Mark ...
... . Поэтому так легко путешествовать по Всемирной паутине (WWW — Worl Wide Web), переходя с сайта на сайт по гиперссылкам. Для отображения в «плоском* тексте смысловых связей между основными разделами или понятиями можно использовать гипертекст. Гипертекст позволяет структурировать документ путем выделения в нем слов-ссылок (гиперссылок). При активизации гиперссылки (например, с помощью щелчка мышью ...
... раза. В силу специфичности информации схемы определения количества информации, связанные с ее содержательной стороной, оказываются не универсальными. Универсальным оказывается алфавитный подход к измерению количества информации. В этом подходе сообщение, представленное в какой-либо знаковой системе, рассматривается как совокупность сообщений о том, что заданная позиция в последовательности ...
0 комментариев