Навигация
Самарский Государственный
Аэрокосмический Университет
им. ак. С.П. Королева
Факультет Производства двигателей летательных аппаратов
Лектор доц.
Расщупкина И.Ю.
Самара 2001г
Химическая т/д.
1) Основные понятия.
Соврем хим т/д разрабатывает наиболее рациональные методы рассчета тепловых балансов при протекании хим и физ-хим процессов. Раскрывает закономерности наблюдаемые при равновесии, определяет наиболее благоприятные условия для т/д-ски возможного процесса, поясняет направление и пределы протекания процессов.
Система т/д – совокупность макротел, взаимод и обменивающ энергией как друг с другом так и с внеш средой.
По характеру взаимод с окр средой делятся на:
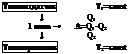
- изолированные (без обмена с внеш средой V=const)
- закрытые (обмен энергией с окр средой m=const)
- открытые (m,V<>const)
Система может быть гомогенной и гетерогенной (однородной и неоднородной)
Совокупность физ и хим свойств системы наз состоянием.
Физ величины, характеризующие состояние системы наз т/д параметрами. Они не зависят от массы системы, их можно измерить напрямую. Их также называют интенсивными свойствами: р, Т, μ – хим потенциал. Экстенсивные св-ва системы зависят от массы системы, их нельзя измерить напрямую, они рассматр как ф-ия параметра состояния и поэтому наз ф-ями состояния: U(вн энер), Н (энтальпия), S (энтропия).
Изменение св-в системы во времени наз процессом.
- сомопроизвольные (протекает без затрат энергии из вне)
- несамопроизвольные(наоборот)
- обратимые (при котором система проходит ряд обращений без изменений в окр среде)
- необратимые (наоборот)
Внутр энерг характеризует общий запас энергии системы и включает все виды энергии движения и взаимод частиц, но не включает кинет энергию вцелом и пот энергию.
Т/д пользуется понятием изменения внутр энергии.
ΔU=Uкон-Uнач dU
Энтальпия характеризует запас энергии системы при р=const она числено равна: H=U+pV
ΔH=ΔU+pΔV dH
ΔH=Hкон-Hнач
Энергия передается от одной системы к другой в виде теплоты и работы. Теплота (Q) не явл ф-ией состояния системы, т.к. ее вел-на зависит от пути перехода системы из нач положения в кон.
Q→δQ, A→δA
Передача теплоты осущ засчет хаотич движения мол-л, а при совершении работы передача энергии идет путем упорядоченного движения мол-л под действием внеш сил
2) 1нач т/д:
В любом процессе приращение внутр энергии системы = кол-ву теплоты, сообщаемой системе за вычетом работы, совершаемой системой.
dU=δQ-δA
δA – сумма всех видов работ, совершаемых системой
δA=pdV+δA’
pdV – работа против внешних сил; δA’ – полезная работа, соверш сист при протекании какого либо процесса
рdV(работу расширения) можно вычислить, если знать у-ия состояния системы
Теплоту процесса подсчитывают, зная истинную теплоемкость системы.
c=δQ/dT
Теплоемкость – отношение б/м кол-ва теплоты, переданного системе к б/м изменению тем-ры им вызываемой.
Следствие 1 нач т/д при p=const
δA=pdV A=pΔV
Q=ΔU+pΔV δQ=dU+pdV=dU+d(pV)=d(U+pV)=dH
Qp=const=ΔH
3)Термохимия – раздел химии, в к-ом изучают тепловые эффекты хим реакции.
При хим реакции происходит изменение внутр энергии путем выделения или поглощения теплоты. В хим процессах работа очень часто незначительна и ей можно пренебречь.
Закон Гесса:
Тепловой эффект х.р. зависит только от вида и состояния исходных в-в и кон продуктов. При термохим рассчетах использ термохим у-ия. Т.х. у-ия обязательно должны содержать молярные кол-ва в-в, в правой части должен быть приведен тепловой эффект, должны быть указаны агрегатные состояния в-в, с т.х. у-иями можно производить все алгебраические действия.
З-н Гесса применим как к хим реакциям так и к физ-хим превращениям (процессам плавления, кристаллизации, испарения, сублимации, конденсации, растворения и т.д.)
При записи з-на Гесса используется два вида тепл эффектов:
1) Энтальпия образования в-в – ΔfH˚ - (тепл эффект реакции образования одного моля данного соединения из простых в-в, взятых в устойчивых стандартных состояниях)
ΔrH˚=ΣконΔfH˚*ni- ΣисхΔfH˚*ni
ΔrH˚ - тепл эффект реакции
ni – стехиометрический коэф
2) Энтальпия сгорания - ΔHсгор - (тепл эффект реакции окисления одного моля данного соединения с кислородом с образованием высших оксидов соответствующих элементов)
ΔrH˚=ΣисхΔHсгор*ni- ΣконΔHсгор*ni
Рассмотрим зависимость теплового эффекта реакции от температуры
Пусть реакция А→В происходит при p=constТепл эффект реакции по з-ну Гесса: ΔrH=HB-HA
Продифференцируем данное у-ие по тем-ре
(dΔrH/dT)p= (dHB/dT)p-(dHA/dT)p
ΔH=Qp
(dΔrH/dT)p=Cp,B-Cp,A – диффер ур-е Кирхгоффа.
Изменение тепл эффекта процесса с температурой = изменению теплоемкости системы, происходящее в результате процесса.
В небольшом интервале температур теплоемкость системы можно считать не зависящей от тем-ры, тогда при p=const, интегрируя дифференциальную формулу (от Т1 до Т2):
ΔHT2=ΔHT1+ΔCP(T2-T1) - интегральное ур-е Кирхгоффа
Т1=298˚К
ΔHT2=ΔH298+ΔCP(T2-298)
По следствию из закона Гесса, изменение теплоемкости находится по следующему соотношению
 ΔCP=ΣконCP*ni- ΣисхCP*ni
ΔCP=ΣконCP*ni- ΣисхCP*ni
4) (2) нач т/д устанавливает направление и условие протекания естественных процессов, для рассчетов наиболее удобной явл формулировка (2) нач т/д, связанная с ростом энтропии.
Вывод (2) нач т/д сделано на основе анализа работы идеальной тепловой машины
η=A/Q1=(Q1-Q2)/Q1=(T1-T2)/T1
Q1/T1-Q2/T2=<0
δQ1/T1-δQ2/T2=<0
dS=δQ/T - приведенная теплота, отражает измен некот фун-ии состояния
(2) нач т/д:
существует некоторое экстенсивное св-во системы S, называемое энтропией, к-ое связано с поглощаемой теплотой и тем-рой системы следующим образом
а) обр dS=δQ/T
б) необр dS>δQ/T
Все самопроизвольные процессы протекают с увеличением энтропии.
Изменение энтропии (ΔS) не зависит от пути перехода из нач состояния в кон, следовательно не зависит от того какой процесс обратимый или необратимый.
При расчетах реальных систем необр процессы можно представл как совокупность множества обратимых.
ΔS=1∫2(δQ/T)обр
Изотермические процессы Т=const
К ним относится фазовое превращение (испарение, конд и т.д.)
ΔS=S2-S1=∫δQ/T=1/T*∫δQ=Q/T
ΔSфаз перех= Qфп/Tфп
Изобарные процессы p=const
Cp= δQ/dT
ΔS=S2-S1=T1∫T2δQ/T=T1∫T2Cp*dT/T=Cp*ln(T2/T1)
ΔSфаз перех= Qфп/Tфп
Энтропия и ее изменение зависят от тем-ры. Нернст пришел к выводу, что вблизи абс 0 изменение энтропии (ΔS) пренебрежимо мало.
Планк сформулировал (3) нач т/д – Постулат Планка:
Энтропия индивидуального кристаллического в-ва при абс 0 = 0
Модель идеального кристалла
Предположим, что тем-ра 1 моля в-ва при p=const увелич от абс 0, где в-во находится в состоянии идеального кристалла, до некоторой тем-ры Т, где в-во находится в состоянии идеального газа. При этом превращение:
| 0˚К | нагрев | плавл | Нагрев | кипение | Нагрев | Т |
| → | Tпл | → | Tкипен | → | ||
| p=const | T=const | p=const | T=const | p=const | ||
| ΔS1 | ΔS2 | ΔS3 | ΔS4 | ΔS5 |
ΔS=ΔST-ΔS0=0˚K∫Tпл(Сp,тв/T)dT+Qпл/Tпл+Tпл∫Tкип(Сp,жид/T)dT+Qкип/Tкип+ Tкип∫T(Сp,газ/T)dT
Величина энтропии Sт, найденное по этому у-ию назыв абс энтропией чистого в-ва при тем-ре Т и атм давлении.
T=298˚К, p=1 атм (стандартные условия) S˚298 из справочника
В хим процессах изменение энтропии подчиняется следствию из з-на Гесса:
ΔrS˚=ΣконS˚*ni-ΣисхS˚*ni
На практике в качестве критерия направленности процесса более удобно использовать другие ф-ии, к-ые назыв т/д потенциалами:
1) изобарно-изотерм пот-л: свободная энергия Гиббса G=H-TS; dG=dH-TdS
2) изохорно-изотрм пот-л: свободная энергия Гельмгольца F=U-TS; dF=dU-TdS
Рассмотрим закрытую систему, в к-ой процесс осущ при T=const.
Согласно (2) нач т/д в такой системе разрешено протекание 2 видов процесса (обр и необр)
T=const
Обратимый
ΔS=Qобр/T
Qобр-TΔS=0; p=const
ΔH-TΔS=0;
ΔG=0 критерий равновесного состояния системы
Необратимый
ΔS>Qнеобр/T
Qнеобр-TΔS=0;
ΔH-TΔS<0;
ΔG<0 критерий самопроизвольности необратимого процесса
Для хим реакций ΔrG˚ рассчитывается по следствию из закона Гесса
ΔrG˚=ΣконΔf*G˚*ni- ΣначΔf*G˚*ni
T=const
Обратимый
V=const; Qv=ΔU
Qобр-TΔS=0
ΔU-TΔS=0 ΔF=0
Необратимый
V=const; Qv=ΔU
Qобр-TΔS=0
ΔU-TΔS<0 ΔF<0
Для процессов, протек при T, р=const, условием самопроизвольного течения явл уменьшение энергии Гиббса. Причем условием их равновесия явл достижение минимального значения для данного условия ф-ии G.
—1 dp=0 dT=0 dG=<0
—2 dV=0 dT=0 dF=<0
В хим т/д большее значение имеет ф-ия, наз хим пот-лом (μi).
μi – ф-ия характеризует состояние к-либо i-компонента в фазе данного состава при опр местных условиях.
Хим пот-л – приращение изобарно-изотермичесокго пот-ла данной фазы при введении дополнит кол-ва i-компонента, при T,р=const и постоянных кол-вах др компонентов, содержащихся в данной фазе.
μi=(дGi/дni)p,T,j=i
G=Σμi*dni
Хим пот-л зависит от концентрации данного компонента и его вида, а также от вида и концентрации др компонентов в этой фазе.
Только в случае идеальн газа хим пот-л опр видом и концентрацией i-компонента и не зависит от концентрации др компонентов.
μi=μi˚+RTln(pini)
pi- парциальное давление i-компонента данной смеси
μi˚- хим потенциал, при парциал давлении =1
ni- кол-во вещества
Общим условием возможности самопроизвольного процесса будет равенство
Σμi*dni=0
Рассмотрим гомоген газ реакцию, к-ая протекает по заданному у-ию
υ1A1+ υ2A2↔ υ3A3+ υ4A4 n=υ
Эта обр хим реакция протекает до тех пор пока не установится равновесие между реагир в-вами. Кол-венно хим равновесие описывается з-ном действия масс.
V1=k1*p A1υ1*pA2υ2
V2=k2*pA3υ3*pA4υ4 V1=V2 условие равновесия
![]()
Закон действия масс
Выражение для хим потенц участников данной реакции
µ1=μ1˚+RTln(p1n1) исх в-ве
μ2=μ2˚+RTln(p2n2) ∆G=μ1+μ2
μ3=… кон в-ве
μ4=… ∆G=μ3+μ4
∆rG=∆конG-∆исхG=(μ3+μ4)-(μ1+μ2)=∆rG˚+RTln((p3υ3*p4υ4)/(p1υ1*p1υ1))
∆rG=∆rG˚+RTlnKP
в усл равнов ∆rG˚=-RTlnKp˚ ∆rG=0
условие нормального сродства или изотерма хим реакции в стандарт условиях. Задавая произвольное значение pi≠1, получаем
∆rG=-RTlnKP+ RTlnПpiгде Пpi=(Пpiкон)/(Пpiисх)
↑ уравнение изотермы химич реакции
хим т/д позволяет определить константу равновесия какой-либо реакции при другой температуре, не ставя дополнительного эксперимента. Для этого существует ур-е изобары.
Ур-е изобары получается при дифференцировании уравнения изотермы химич реакции по температуре, и комбинировании полученного ур-я с ур-ем Гиббса-Гельмгольца
ΔG=-RTln(K˚)+RТln(Пpi)
ΔG=ΔH-T(дΔG/дТ)
dln(Kp)/dT=ΔH/(RT2) изобара
dln(Kс)/dT=ΔU/(RT2) изохора
Чтобы получить удобное для расчета мат выражение для ур-я изобары следует проинтегрировать дифференцированную форм; предполагая, что в небольшом интервале температур Т1–Т2 тепловой эффект реакции от температуры не зависит. Тогда получаем интегральную форму
ln(K1/K2)=ΔH(T1-T2)/(R*T1*T2) интегральная форма изобары
Следствия:
1) Можно рассчитать константу равновесия при Т2, отличающуюся от Т1 если известна К1 и тепловой эффект реакции в этом интервале темпер
2) Можно рассчитать тепловой эффект реакции если известны константы равновесия хотя бы при двух температурах
3) С помощью уравнения подтверждается вывод и- принципа смещения равновесия Ле-Шателье (влияние на константу равновесия температуры )
Если на систему, находящуюся в равновесии оказывать внешнее воздействие, то равновесие сместится в сторону реакции, противодействующей внешнему влиянию
3H2+N2=2NH3-ΔH
(г) (г) (г)
- увеличение P → прямая
- увеличение Т → обратная
ln(K1/K2)=(ΔH/R)*(T1-T2)/(T1*T2)
Химическая кинетика
Кинетика хим реакций– учение о скорости их протекания и зависимости ее от различных факторов. Такие факторы: строение молекулы, концентрация участников реакции, температура, свойства среды, наличие катализатора, внешние воздействия.
По правилам ИЮПАК скорость химической реакции определяется как возрастание степени завершенности реакции V=dξ/dτ
Более удобно понятие скорости образованя или преварщения некоторого компонента в системе Vi=±dCi/dτ
Влияние концентрации на скорость описывается законом действующих масс
Скорость реакции пропорционально произведению концентраций веществ, взятых в степенях, равных стехиометрическим коэффициентам
V=K*C1n1*C2n2*…*Cini
Вид уравнения зависит от того, как протекает реакция
А+2В=С V=K*CА1*CВ2
N2+3H2=2NH3
V=K*CN2*CH23
К– коэффициент пропорциональности химических реакций
Физический смысл константы скорости – скорость химической реакции при единичной концентрации компонента. Сумма показателей степеней ΣNi=n: общий порядок реакции
Показатель ni называется порядком реакции по i-тому компоненту
В простых реакциях в одну стадию ni– целое число и его значение совпадает с молекулярностью реакции
Молекулярность определяется числом молекул в элементарном хим акте (целое положительное число (1,2,3)); элементарных актов с учатием 4-х молекул не бывает
Влияние темперауры
При повышении Т процесса на каждые 10˚ скорость реакции в области умеренных температур увеличивается 2-4 (Вант-Гофф)
V2/V1=K2/K1=γ — отношение констант скорости (γ=2–4) реакций при 2-х температурах, отличающихся на 10˚ V2=V1*γ(T2-T1)/10
А+В=С
Т1→V1=K1*CA*CB
Т2→V2=K2*CA*CB
Аррениус показал, что К зависит от температуры и эта зависимость описывается: dln(K)/dT=Еакт/(RT2) Еакт– энергия активации
Предполагая, что Еакт не зависит от природы веществ проинтегрируем данное уравнение К=Ае-(Еакт/RT) A– предэкспотенциальый множитель
Для расчета Еакт и А проводят экспериментальное определение констант скоростей, при некоторых температурах и строят график зависимости lnK=f(1/T)
Графический способ определения энергии активации.
Энергетический способ определения энергии активации.
Записывая ур-е Аррениуса для 2-х температур, но для одной реакции; делят ур-е почленно при этом сокращается А; частное ,полученное от деления логарифмируем и преобразуем в формулу с выделением Еакт.
Физический смысл энергии активации
Аррениус высказал, что молекулы вступают во взаимодействие при столкновении друг с другом (разлетаются, сцепляются). Не все столкновения результативны, эффективны только столкновения между молекулами, обладающими некоторым избытком внутренней энергии по сравнению со средним значением для данной температуры. Этот избыток энергии Аррениус назвал энергией активации.
Гипотеза Аррениуса легла в основу теории активных соударений. Согласно этой теории в равнении Аррениуса А= общему числу столкновений за единицу времени. Ае-(Еакт/RT)– число активных соударений. Теория активных соударений хорошо описывает уравнения в газовой фазе. Для реакций в жидкой фазе была разработана теория переходного состояния. Основное положение теориии: при элементарном акте химической реакции образуется промежуточный активный комплекс с неустойчивыми связями и существующий очень короткое время. В результате акта комплекса с другими молекулами происходит разрушение валентных связей и комплекс распадается с образованием продуктов реакций (А+В)↔(А…В) (А…В)↔(А+В)
Кинетические уравнения
-dc/dt=k*Cn –порядок реакции®кинетическое уравнение в дифференц форме
Реакции (1) порядка (n=1)
Со – нач концентрация реагир в-ва
С - текущая концентрация
-dc/dt=k*C
Со∫С-dC/C=0∫tkdt
ln(C0/C)=k*t кин ур-е I порядка в интегр форме
Определение константы скорости реакции (1) порядка:
1) метод подстановок
В разные моменты времени опр концентрация реагир в-ва, подставляют эту концентрацию в у-ие и соответственно рассчитывают константу скорости
2) графический метод
3) по времени полупревращения
Временем полупревращения реакции (t1/2) наз время, за к-ое концентрация реагирующего в-ва, равная вначале Со, уменьшается вдвое, т.е. до1/2* Со
K=(2.303/ t1/2)*lg(Со/(1/2* Со))= (2.303/ t1/2)*lg2=0.693/t1/2
t1/2=0.693/k
Для любой конкретной реакции (1) порядка время полупревращения явл константой и не зависит от нач концентрации.
Реакции (2) порядка (n=2)
Кинетич у-ию (2) порядка подчиняется реакция следующего типа:
1)- 2A→прод реакц
2)- A+B→прод реакц CA=CB
-dc/dt=k*C2
Со∫С-dC/ C2=0∫tkdt
-1/C0+1/C=kt 1/C=1/C0+kt кин ур-е II порядка в интегр форме
k=1/t*((C0-C)/(C0*C))
Определение константы скорости реакции (2) порядка:
1) метод подстановок
В разные моменты времени находим текущую концентрацию, подставляют эту концентрацию в у-ие и соответственно рассчитывают константу скорости
2) графический метод
3) по времени полупревращения
Для реакции (2) порядка время полупревращения обр-пропорц нач концентрации
k=1/t1/2*((C0-(1/2)*C)/(C0*(1/2)*C))
k=1/t1/2*(1/C0) → t1/2=1/(k*C0)
Для реакций II порядка время t1/2 обратно пропор начальной концентр (C0)1 и (C0)2
(t1/2)1/(t1/2)2=(C0)2/(C0)1 реакция II порядка
Катализ и катализаторы
Катализ – явление селективного изменения скорости хим реакции по средствам катализатора.
Катализатор – в-во, изменяющ скорость хим реакции, участвующее в ней , но к моменту образования продуктов реакции кол-во и состав катализатора остается неизменным.
Особым видом явл автокатализ – скорость хим реакции изменяется под действием продуктов реакции.
Различ катализаторы:
- гомогенные (находятся с реагир в-вами в одной фазе)
- гетерогенные (находятся в другой фазе, чем реагир в-ва)
Они также бывают:
- положительные (увелич скорости хим реакции)
- отрицательные – ингибиторы (уменьш скорости хим реакции)
Хар-ки кат-ра:
а) активность или производительность A-активность
А=mпрод/(t*mкат) А=mпрод/(t*Sкат) А=mпрод/(t*Vкат)
б) селективность или избирательность
HC≡CH→(H2)→ H2C=C H2→(H2)→ H3C-CH3
C2H5OH →Al2O3→ C2H4+H2O
C2H5OH →Ag, Cu→ CH3CHO+H2
S(селективность)=mцелевого продукта/mвсех продуктов
Общие закономерности катализа:
1) применение кат-ра не изменяет т/д кинетич реакции, т.е. вел-ны ∆H и ∆G
- кат-р ускоряет только те хим реакции, для к-ых ∆G<0
- кат-р ускоряет достижение состояния равновесия в случае обратимых хим реакций, но не смещает равновесие и не изменяет величины константы
- применение кат-ра не изменяет тепл эффект хим реакции, т.е. ∆H
2) Кат-р уменьшает полную энергию активации реакции, т.к. каталитическая реакция идет по др пути.
А+В→АВ
А+В→А … В→АВ – без катализатора
А+В+катал→А …кат-ор … В→АВ – с катализатором
Растворы Коллегативные свойства растворовКоллегативные свойства растворов - свойства раствора связанные друг с другом и обусловленные общими причинами, главным из которых является число растворенных частиц в растворе.
К таким свойствам относятся: понижение давления насыщенного пара растворителя над раствором, увеличение температуры кипения, уменьшение температуры кристаллизации, осмотическое давление
I закон Рауля
Относительное понижение давления насыщенного пара растворителя над раствором равно мольной доле растворимого вещества
![]() А – растворитель
А – растворитель
В – растворенное вещество
![]() pA°–давление насыщ пара с растворителем над растворителем
pA°–давление насыщ пара с растворителем над растворителем
pA–давление насыщ пара с растворителем над раствором
Следствие
понижение давления насыщенного пара растворителя над раствором является понижением температур кристаллизации и повышения температур кипения
II закон Рауля
Депрессия кипения или кристаллизации (ΔTкр, ΔTкип) прямо пропорциональна концентрации растворенного вещества
![]()
![]()
![]()
![]()
моляльная масса
Е (эбуллиоскопическая константа) характеризует свойства растворителя и численно равна депрессии кипения одномолярного раствора
EH2O=0,520![]()
К (клиоскопическая константа) характеризует свойства растворителя и численно равна понижению температуры кристаллизации одномолярного раствора.
KH2O=1,860![]()
Депрессия кипения и кристаллизации величины положительные
Е и К связаны с температурой кипения и кристаллизации растворителя, а также с их удельной теплотой парообразования и плавления соответственно
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Измеряя температуру кипения и температуру кристаллизации можно определить молекулярную массу растворенного вещества
![]()
Если привести в соприкосновение два раствора различной концентрации или раствор и растворитель, то движение частиц растворенного вещества станет направленным.
Осмометр
Молекулы растворителя проникают через полупроницаемую мембрану, что сопровождается повышением уровня жидкости во внутреннем сосуде осмометра. При этом создается препятствующее осмосу гидростатическое давление столба жидкости; на некоторой высоте h гидростатическое давление становиться таким, что осмос прекращается – наступает осмотическое равновесие.
Осмотическое давление – это давление численно равное минимальному гидростатическому давлению, которое нужно приложить к жидкости, чтобы осмос прекратился
![]()
![]()
Комбинируя две последних формулы, получим формулу для расчета молекулярной массы растворенного вещества.
Растворы электролитовКоличественный процесс диссоциации характеризуется степенью диссоциации и константой диссоциации
Степень диссоциации (ионизации) [a] – отношение числа молекул распавшихся на ионы к общему числу молекул.
![]()
![]()
![]()
Константа диссоциации описывает равновесие процессов диссоциации и определяется законом действующих масс
CH3COOH«CH3COO–+H+
![]()
Используя a можно записать:
[CH3COO–]=[H+]=a*C0, кисл
[CH3COOH]=C0, к-ты-a* C0, к-ты=(1-a)*C0, к-ты
![]()
Если заменить концентрацию через разведение С=1/V
![]() Если a<3%Þ1-a@1
Если a<3%Þ1-a@1
![]()
![]()
С разведением раствора слабого электролита степень его диссоциации возрастает. Сильные электролиты этому закону не подчиняются. Было установлено, что вычисляемая по этому уравнению константа диссоциации зависит от концентрации раствора; увеличение концентрации ионов в растворе вызывает увеличение интенсивности их взаимодействия между собой и с растворителем.
Отклонение от идеальных растворов учитывают с помощью коэффициента активности γ.
Коэффициент активности (γ) показывает во сколько раз активность раствора или его эффективная концентрация отличается от общей концентрации вещества.
Классическая константа диссоциации записывается с учетом коэффициента активности
![]()
![]()
![]()
В технике часто используют системы, состоящие из труднорастворимого электролита в виде осадка и раствора над ним. В таких системах устанавливается равновесие.
AgCl(тв)®Ag(р-р)++Cl(р-р)–
![]()
Активность чистой твердой фазы, при каждой данной температуре является константой
![]()
, где (ПР) – произведение растворимостей
Постоянство произведения растворимости не означает, что активность ионов электролита в растворе должна быть неизменной
При добавлении к раствору хлорида серебра нитрата серебра, которые содержат одноименные ионы, увеличивается скорость обратной реакции, и часть ионов серебра выпадает в виде осадка.
AgNO3®Ag++NO3–
При этом соблюдается следующее условие: Произведение концентрации ионов в растворе больше произведения растворимостей
Общее условие равновесия. Правило Гиббса. Однокомпонентные системы диаграмм состояния водыКристаллизация растворов. Термический анализ.
Фаза – совокупность гомогенных частей системы одинаковых по составу химическому составу и физическим свойствам и отделенных от других частей системы поверхностью раздела.
Равновесие между фазами в гетерогенной системе называется гетерогенным или фазовым равновесием, особенностью многофазовых систем является равенство химических потенциалов веществ, температур и давлений во всех фазах
![]()
![]() парообразование
парообразование
![]() конденсация
конденсация
Компонент – индивидуальное химическое вещество, которое является составной частью системы, может быть выделенным из нее и может существовать самостоятельно
Число компонентов – наименьшее число индивидуальных химических веществ, необходимых для образования всех фаз в гетерогенной системе и для математического описания любой фазы.
Состояние системы характеризуется числом свободы или вариантностью системы
Пусть n-фаз содержит k-компонентов, а состояние каждой фазы определяется числом компонентов
С=К-Ф+2 (закон фазового равновесия, правило Гиббса)
Число степеней свободы равновесной термодинамической системы, на которую влияют только температура и давление равно числу независимых компонентов минус число фаз плюс 2
Число степеней свободы характеризует число независимых переменных, которые можно произвольно менять в определенных пределах без изменения числа и агрегатного состояния фаз в системе
Для конденсированных систем закон Гиббса имеет вид С=К-Ф+1
Построение Диаграмм
Графическое построение зависимостей p=f(T), p=f(C), T=f(C) позволяет определить число фаз, границы их существования, характер взаимодействия без выделения самих индивидуальных компонентов.
Исследование диаграмм построено на двух принципах:
Похожие работы
... и осуществлялись им с исключительной строгостью Экспериментальных данных Вюрца впоследствии никто не опровергал, они были безукоризненны. С первыми теоретическими работами Вюрц выступил в 40-е годы XIX в.— время становления теоретических основ химии, когда подрывались принципы дуалистической системы и теории сложных радикалов, когда трудами французских химиков Дюма, Лорана и Жерара закладывались ...
... г. для химической лаборатории построено отдельное здание. При чтении лекций в это время профессора придерживаются большей частью руководств Теннара, Пайена, Розе, Пфаффа и Берцелиуса. Следовательно, новое направление химии в России было усвоено весьма скоро. К этому же времени относится и появление, кроме переводных, также и первых оригинальных руководств по химии на русском языке. В 1810 - 1813 ...
... свежесорванных растениях массовая доля сухого вещества составляет (100–82,5)=17,5%. Тогда 100 г сырья – 17,5 г сух. раст. матер. х г сырья – 17,7 г сух. раст. матер. Отсюда х = 100•17,7/17,5 = 100,1 г. химия медицина курс Поскольку в настоях и отварах трав абсолютно точно дозировать содержание лекарственного вещества невозможно, с достаточной степенью точности можно принять, что необходимое ...
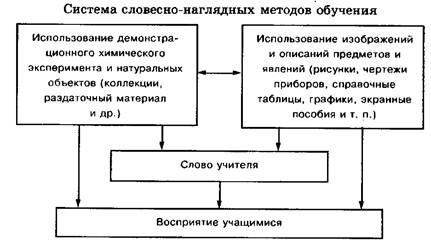
... экономики» и др. Семинар - это метод, сближающий школьные формы работы с вузовскими, и для старшеклассников он полезен [5-7]. 4. СИСТЕМА СЛОВЕСНО-НАГЛЯДНЫХ МЕТОДОВ ОБУЧЕНИЯ ХИМИИ И ИХ ВЗАИМОСВЯЗЬ СО СРЕДСТВАМИ НАГЛЯДНОСТИ Словесно-наглядные методы обучения определяют использование в учебном процессе различных средств наглядности в сочетании со словом учителя. Они непосредственно связаны со ...
0 комментариев