Сложение двух колебаний одного направления

1. Сложение двух колебаний одного направления.

а) сложение 2-х колебаний одинаковой частоты.

ω₁ = ω₂ = ω, Т₁ = Т₂ = Т Уравнения колебаний отличаются только начальной фазой и амплитудой и имеют вид:

Представим оба колебания в виде векторов амплитуды Х₀₁ и Х₀₂, Сложение векторов выполним графически.

Отложим от точки 0 под углом φ₁ – вектор Х₀₁, под углом φ₂ – вектор Х₀₂. Обе амплитуды вращаются с одинаковой угловой скоростью и против часовой стрелки. Следовательно, угол между амплитудами остается постоянным, равным (φ₂ – φ₁). Вектор Х₀ представляет собой гармоническое колебание, происходящее с той же частотой и амплитудой │Х₀│= │Х₀₁+ Х₀₂│ и начальной фазой φ. Из чертежа

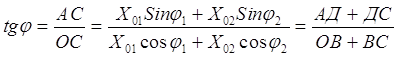
Само результирующее колебание имеет вид:

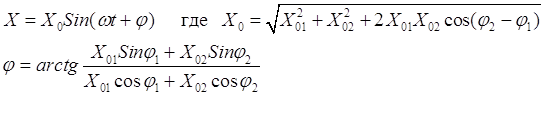
Важно заметить, что амплитуда результирующего колебания зависит от разности фаз (φ₂ – φ₁) слагаемых колебаний.

Она заключена в пределах:

1)         Если разность начальных фаз слагаемых колебаний, равна четному числу π, φ₂ – φ₁ = кπ , то Х₀ = Х₀₁ + Х₀₂, tg φ = tg φ₁, φ = φ₁, к = 0,1,2, …

Колебания однофазные и усиливают друг друга.

2) Если φ₂ – φ₁ = (2к+1)π , то Х₀ = Х₀₁ - Х₀₂ , к = 0,1,2,… следовательно колебания ослабляют друг друга

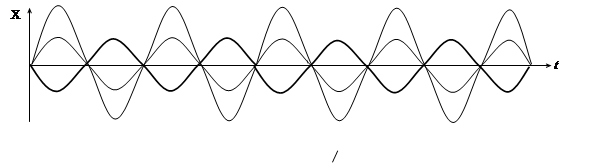
3) Если Х₀₁ = Х₀₂ , ω₁ = ω₂ = ω , φ₂ = φ₁

Уравнение результирующего колебания имеет вид:

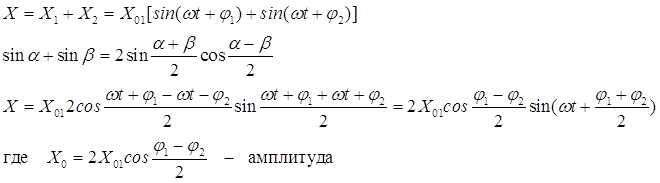
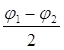 – начальная фаза результирующего колебания.

Результирующее колебание гармоническое, отличающееся по фазе от слагаемых колебаний на половину суммы их начальных фаз.

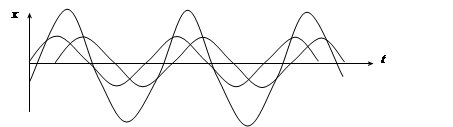
При φ₁ – φ₂ = 2кπ , (к = 0,1,2,…) Х₀ = 2Х₀₁ – колебания усиливаются.

При φ₁ – φ₂ = (2к + 1)π , (к = 0,1,2,…) Х₀ = 0 – колебания гасятся.

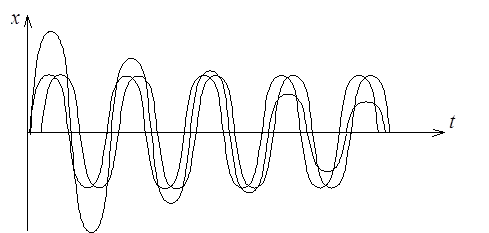
2. Биения.

 

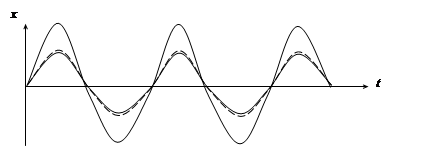
Особый интерес представляет сложение колебаний одинакового направления с одинаковыми амплитудами, имеющими (близкие) мало отличающиеся частоты.

Результирующее суммарное колебание имеет уравнение:

Полученное выражение представляет собой произведение 2-х гармонических сомножителей с частотам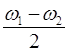и  и .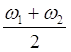

Если ω₁ мало отличается от ω₂ , то частота 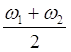 имеет близкие значения к ω₁ и ω₂ , а частота 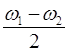– будет очень мала, т.е.

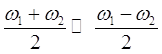
Отсюда следует, что результирующее колебание можно рассматривать как гармоническое колебательное движение, происходящее с круговой частотой 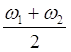 , периодом  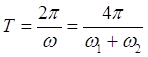и амплитудой

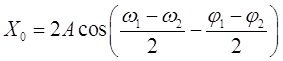
Причем амплитуда не остается постоянной, а медленно изменяется со временем. Частота изменения амплитуды  ,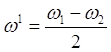

а период амплитуды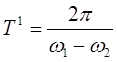

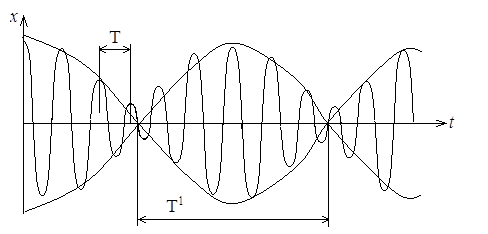
Такие колебания называются биениями. Биения - такие колебания, амплитуда которых периодически возрастает и убывает по закону cos. Максимальная амплитуда наблюдается, если фазы слагаемых колебаний совпадают. Ясли эти колебания находятся в противофазе, то они гасят друг друга.

Биения часто встречаются при сложении колебаний и широко используются в радиотехнике.

3.      Сложение взаимно перпендикулярных колебаний.

 

1)         Рассмотрим движение точки М₁, участвующей одновременно в 2-х взаимно перпендикулярных колебаниях, частоты которых ω₁ и ω₂ равны (ω₁ = ω₂ = ω), амплитуды соответственно а и в.

Колебательный процесс в этом случае описывается системой уравнений:

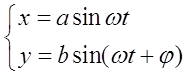
где φ – угол сдвига фаз.

Для определения уравнения траектории движения точки из системы уравнений исключим время. Из первого уравнения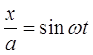

Второе уравнение перепишем в виде:

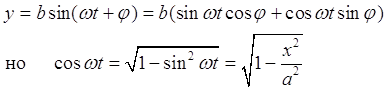
Подставив вместо sin ωt и cos ωt их значения будем иметь уравнение движения

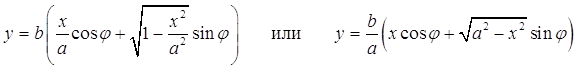
Исследуем некоторые частные случаи.

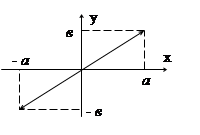
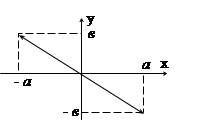
а) при равенстве частот имеет место еще и равенство фаз, т.е. φ = 0.

Уравнение траектории имеет вид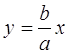

Уравнение прямой, проходящей через начало координат под углом ά: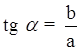

Смещение от начала координат определяется уравнением

Т.к. уравнение слагаемых колебаний имеет вид

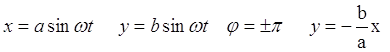
Таким образом результирующее движение является гармоническим колебанием.

б) составляющая колебания отличается по фазе на π/2 . Уравнение траектории имеет вид: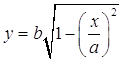

отсюда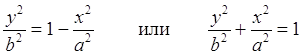  

- эллипс с плоскостями a и b.

При равенстве амплитуд траектории представляют собой окружность.

 

 

 

 

 

 

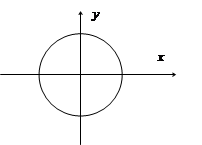
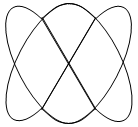
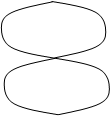
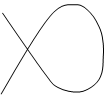
2) При сложении взаимно перпендикулярных колебаний, частоты которых кратны между собой, например ω₁ : ω₂ = 1/2 , 2/3 и т.д. = m/n ,

где m и n – целые числа, колеблющееся тело описывает сложные кривые (наз. Фигурами Лисажу), форма которых определяется отношением частот складываемых колебаний, их амплитудой и разностью фаз между ними

ω₁ : ω₂ = 2 : 1 ω₁ : ω₂ = 3 : 2

Δφ = 0 Δφ = π / 2 Δφ = 0 Δφ = π / 4