Навигация
Принятие решения приемником по одному отсчету
3.3. Принятие решения приемником по одному отсчету
Сообщения передаются последовательностью двоичных символов «1» и «0», которые появляются с априорными вероятностями Р(1) = 0,6 и Р(0) = 0,4. Этим символам соответствуют канальные сигналы S1(t) и S2(t), которые точно известны в месте приема.
В канале связи на передаваемые сигналы воздействует гауссовский стационарный шум с дисперсией σ2 = 1,65 10-5 . Приемник, оптимальный по критерию идеального наблюдателя (минимума средней вероятности ошибки), принимает решение по одному отсчету смеси сигнала и помехи Z(t0) = Si(t0) + ξ(t0) на интервале элемента сигнала длительности Т.
Для принятия решения по критерию идеального наблюдателя используется отношение правдоподобия λ, которое определяется выражением:
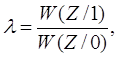
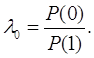 |
где W(Z/1) и W(Z/0) – условные функции плотности вероятности; и пороговое отношение правдоподобия λ0, равное
Правило принятия решения в данном случае будет следующим:
Если λ >λ0, то решение принимается в пользу сигнала «1», иначе – в пользу сигнала «0».
Для применения критерия идеального наблюдателя необходимо выполнение следующих условий:
1. Сигналы должны быть полностью известны;
2. Действие в канале связи помехи с гауссовским законом распределения ;
3. Должны быть известны априорные вероятности сигналов.
Плотности вероятностей W(Z/1) и W(Z/0) рассчитываются по формулам:
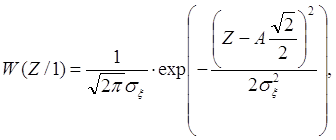 | |||
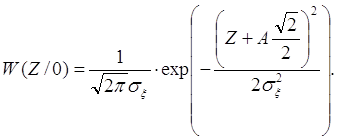 | |||
Найдем отношение правдоподобия λ:
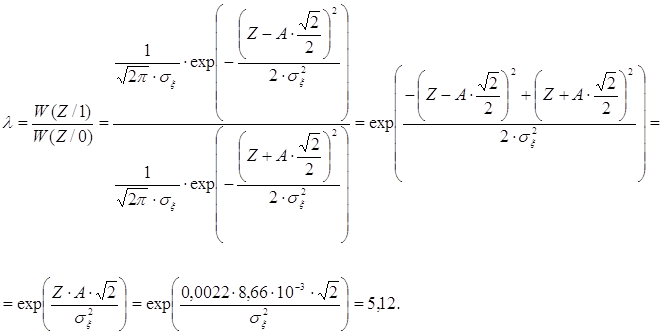
Пороговое отношение правдоподобия λ0 = 0,4/0,6 = 0,67. Используя правило принятия решения, получаем 5,12 > 0,67, т.е. λ >λ0, следовательно, передавался сигнал «1».
По формулам для W(Z/1) и W(Z/0) рассчитаем значения и построим графики функций W(Z/1) и W(Z/0).
Результаты расчетов сведем в таблицу
| Z x10-3 | 12 | –10 | –8 | –6 | –4 | –2 | –1 | 0 | 1 | 2 | 4 |
| W(Z/1) | 0 | 0,04 | 0,23 | 1,15 | 4,42 | 13,34 | 21,19 | 31,65 | 44,50 | 58,87 | 85,93 |
| Z x10-3 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 |
| W(Z/1) | 98,42 | 88,46 | 62,39 | 34,53 | 15,01 | 5,11 | 1,36 | 0,28 | 0,05 | 0,006 | 0 |
| Z x10-3 | –26 | –24 | –22 | –20 | –18 | –16 | –14 | –12 | –10 | –8 | –6 |
| W(Z/0) | 0 | 0,006 | 0,05 | 0,28 | 1,36 | 5,11 | 15,01 | 34,53 | 62,39 | 88,46 | 98,42 |
| Z x10-3 | –4 | –2 | –1 | 0 | 1 | 2 | 4 | 6 | 8 | 10 | 12 |
| W(Z/0) | 85,93 | 58,87 | 44,50 | 31,65 | 21,19 | 13,34 | 4,42 | 1,15 | 0,23 | 0,04 | 0 |
Плотность распределения вероятности помехи W(ξ) рассчитаем по формуле:
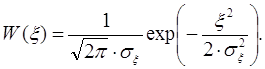
Результаты расчетов сведем в таблицу
| ξx10-3 | –18 | –16 | –14 | –12 | –10 | –8 | –6 | –4 | –2 | –1 | 0 | 1 |
| W(ξ) | 0 | 0,04 | 0,26 | 1,25 | 4,76 | 14,16 | 33,07 | 60,63 | 87,23 | 95,53 | 98,47 | 95,53 |
| ξx10-3 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| W(ξ) | 87,23 | 60,63 | 33,07 | 14,16 | 4,76 | 1,25 | 0,26 | 0,04 | 0 |
Похожие работы
... . 1.2. Если в данный момент времени , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет ...
... к расчету. ¨ В оглавлении указываются названия разделов и номера страниц, соответствующие началам разделов. ¨ Во введении кратко рассматривается общенаучное значение теории электрических цепей (ТЭЦ) для изучения электромагнитных явлений и их практического приложения. Описываются связи ТЭЦ с соответствующими разделами математики и физики, а также с различными ...
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
... Мгновенное напряжение на проводимости G =10 Cм при заданном токе i=12sin(ωt+φ) равно: u=1,2sin(ωt + φ) 4. Электрические цепи при гармоническом воздействии в установившемся режиме Основные свойства линейных цепей: Принципа суперпозиции. Независимыми называют узлы, которые: отличаются одной ветвью. Независимыми называются контура, которые: отличаются одной ...







0 комментариев