Навигация
Процедура качественной оценки экологических воздействий и её использование при разработке экспертной системы
3. Процедура качественной оценки экологических воздействий и её использование при разработке экспертной системы
В ряде экологических проблем часто достаточно качественно оценить экологические воздействия, особенно, более существенные и определить причинно-следственные связи между воздействиями (человека, например) и вектором состояния экосистемы x, x=(x(1), x(2), ... , x(n)), где х(i) - фактор экологического состояния, i=1,2,...,n. Такого рода модели не позволяют нам оценить всю сложную и динамическую цепь взаимовлияний экологических параметров среды, но являются когнитивным инструментарием на начальных стадиях исследования экосистемы, например, на этапе формализации и структурирования системы.
Предлагается следующая процедура моделирования. Выбирается, например, экспертным путем вектор состояния экосистемы x=(x(1),x(2),...,x(n)) , - рассматриваемая область (или экониша), а также граничные векторы состояния среды a=(a(1),a(2),...,a(n)), b=(b(1), b(2),...,b(n)), где a(i)=min{x(i)}, b(i)=max{x(i)} . Составляется матрица V из элементов v(i,j), где v(i,j) - степень влияния x(i) на x(j), i=1,2,...,n. При этом можно использовать, например, модели корелляционного анализа, графовые или же динамические [4]. Далее выбираем начальное состояние х(0) и проводим имитационные расчеты по заданной временной сетке. Управление моделью (траекторией эволюции системы) можно осуществлять изменениями параметров x(i), a(i), b(i), v(i,j) или моделей взаимодействия, выбираемых из некоторого банка моделей [4], а также динамическим переупорядочиванием связей в экосистеме (модели). Наконец, оцениваем эффективность j-ой траектории (имитационного варианта номер s, приводящего к решению номер r, 1 r R): E(r) = c(s)g(s, r; x), c(s)=1, 1 r N, где суммирование ведётся от 1 до R, c(s) - экспертная оценка значимости цели номер s, g(s, r; x) - функционал эффективности траектории s приводящей к цели r. Определяем вероятность p(z, k) предпочтения траектории номер z другой траектории с номером k и функция правдоподобия этого предпочтения W:
d(z, k) N-d(z, k)
p(z, k)= p(k)/(p(k)+p(z)), W= p(z, k) (1-p(z, k)) ,
z<k
где N- число траекторий, p(z) и p(k) - вероятности предпочтений для траекторий номер z, k, соответственно, d(z, k) - экспертная (сравнительная) оценка траекторий z и k (его можно взять, в частности, равным сумме оценок или баллов, при которых траектория z предпочиталась траектории k).
Заметим, что более сложная и формализованная модель получается, если:
1) использовать гипотезу - воздействия или отклики воздействий образуют марковскую цепь {Х(j,h(j))}, j=1,2,...,J с матрицей переходных вероятностей h(j) из элементов h(j; z, k);
2) повторять имитационные расчеты с различными вероятностями p(z) и p(k), уточняемыми каждый раз, например, следующим образом (q(z) - экспертная оценка траектории z, например, сумма баллов, в которой отмечалась траектория номер z ): p(z):=q(z)/(N (1/(p(z)+p(j)))). Суммирование ведётся по всем z=1, 2,…, J, z k.
Данная процедура и её модификации позволяют построить экспертные системы прикладной экологии. Одна из таких систем построена автором и Тебуевым М. c использованием аппарата нечетких множеств и нечеткой логики [5]. Не вдаваясь в принципы разработки, укажем одну её предметную область.
Пусть для определения экологических факторов деятельности человека выбраны n воздействий человека на среду и набор из m индикаторов состояния, наиболее важные (по мнению ряда экспертов). В качестве тестового примера будем использовать, в соответствии с вышеприведенным принципом 3, данные работы [6]. Воздействие, соответствующее каждому действию и каждому фактору описывается через амплитуду и важность. Амплитуда - это мера общего уровня, масштаба воздействия, а важность - мера значимости данного действия в конкретном случае. Это позволяет отделить фактические данные об амплитудах от субъективных оценок важности. Амплитуда оценивается от -10 до 10. Амплитуда положительна (отрицательна), если влияние воздействия полезно (вредно). Важность измеряется в баллах от 0 до 9: 0 - максимально отрицательное воздействие, 1 - значительно отрицательное, 2 - выраженное отрицательное, 3 - некоторое отрицательное, 4 - слабое отрицательное, 5 - слабое положительное, 6 - некоторое положительное, 7 - выраженное положительное, 8 - значительное положительное, 9 - максимально положительное.
Приведем сценарий диалога с экспертной системой.
Экспертная система (04.06.1996 - Вторник, 11: 23: 37)
Входные данные:
1. Контроль над эррозией: 0.6
2. Сооружения для отдыха: 0.1
3. Ирригация: 0.9
4. Сжигание отходов: 1.0
5. Строительство мостов и дорог: 0.6
6. Искусственные каналы: 0.5
7. Плотины: 0.3
8. Туннели и подземные сооружения: 0.9
9. Взрывные и буровые работы: 0.45667
10. Открытая разработка: 0.567
11. Вырубка лесов: 0.345
12. Коммерческая охота и рыбная ловля: 0.234
13. Растениеводство: 0.678
14. Разведение и выпас скота: 0.648
15. Химическая промышленность: 0.2456
16. Лесопосадки: 0.54846
17. Удобрения: 0.6
18. Разведение и регулирование диких животных: IGNORE
19. Автомобильное движение: 0.6
20. Трубопроводы: 0.0
21. Хранилища отходов: 0.0
22. Использование ядохимикатов: 0.2
23. Течи и разливы: 0.0
Выходные данные (принятие решения):
1. Состояние почвы: 0.55177 (слабое положительное)
2. Состояние поверхностных вод: 0.52969 (слабое положительное)
3. Качественный состав вод: 0.62299 (некоторое положительное)
4. Качественный состав воздуха: 0.61298 (некоторое положительное)
5. Температура воздуха: 0.48449 ( слабое отрицательное)
6. Эррозия: 0.59051 (слабое положительное)
7. Деревья и кустарники: 0.54160 (слабое положительное)
8. Травы: 0.59051 (слабое положительное)
9. Сельхозкультуры: 0.51698 (слабое положительное)
10. Микрофлора: 0.48702 (слабое отрицательное)
11. Животные суши: 0.59804 (слабое положительное)
12. Рыбы и моллюски: 0.51525 (слабое положительное)
13. Насекомые: 0.56000 (слабое положительное)
14. Заболачивание территории: 0.50000 (слабое положительное)
15. Курорты на суше: 0.52729 (слабое положительное)
16. Парки и заповедники: 0.54668 (слабое положительное)
17. Здоровье и безопасность: 0.62870 (некоторое положительное)
18. Занятость людей: 0.51196 (слабое положительное)
19. Плотность населения: 0.55539 (слабое положительное)
20. Соленость воды: 0.48750 (слабое отрицательное)
21. Солончаки: 0.57000 (слабое положительное)
22. Заросли: 0.62935 (некоторое положительное)
23. Оползни: 0.70588 (выраженное положительное)
Список литературы
Казиев В.М. Математические и компьютерные модели экологических систем. Тезисы докладов региональной научной конференции “Современные проблемы экологии”, часть 2, Краснодар-Анапа, 1996, с.87.
Большаков В.Н., Криницин С.В., Кряжимский Ф.М., Мартинес Рика Х.П. Проблемы восприятия современным обществом основных понятий экологической науки. “Экология”, N 3, 1996, с. 165-170.
Пых Ю.А., Малкина-Пых И.Г. Об оценке состояния окружающей среды. Подходы к проблеме. “Экология”, N 5, 1996, с.323-329.
Казиев В.М. Некоторые оптимизационные задачи управления экосистемами. Доклады А(Ч)М АН, N 1, 1994, с. 19-21.
Прикладные нечеткие системы. Под редакцией Т.Тэрано, К.Асаи, М.Сугэно. М., Мир, 1993.
Экологические системы. Адаптивная оценка и управление. Под ред. К.С.Холинга. Мир, 1981.
Похожие работы
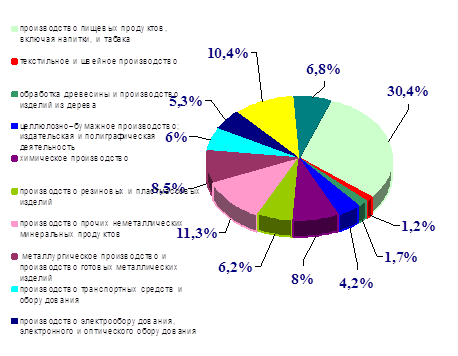
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
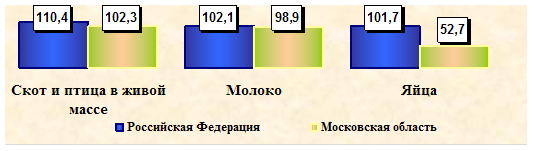
... , Раменский, Наро-Фоминский, Мытищинский, Одинцовский и Рузский муниципальные районы, а также в городские округа Химки, Дубна, Балашиха, Домодедово и Котельники. 3. Прогнозирование социально-экономического развития Московской области Показатели прогноза разработаны на базе статистических данных за 2001–2007 годы, а также с учетом тенденций, складывающихся в экономике и социальной сфере ...
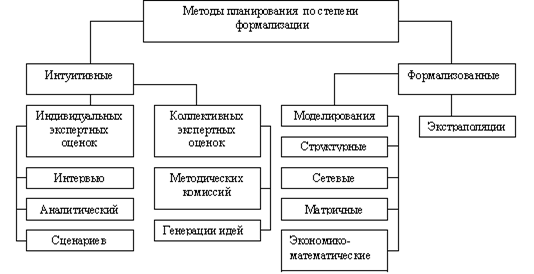
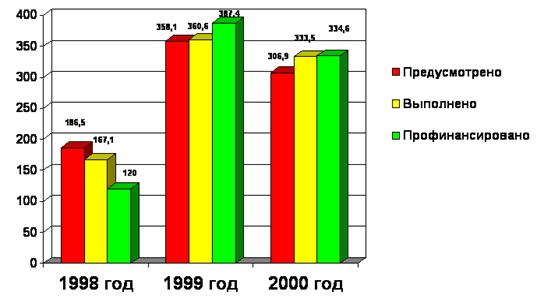
... развития промышленности области, без прогнозно-плановых показателей товаропроизводителей она является необоснованной, то есть нарушается неоднократно упоминавшийся принцип обратной связи. Недостатком сегодняшнего планирования промышленного комплекса является, как ни странно, отсутствие целевых установок и обоснования необходимости достижения именно запланированного уровня показателей. Так, целью ...
... являются: - носитель идей планирования - средние и низшие уровни менеджмента, - задача планирования - обеспечение относительной надежности и относительного структурирования, - горизонт - короткие и средние сроки, - глубина - детализация планов, - диапазон - ограниченный спектр альтернатив, - основа - созданный потенциал. Оперативным планированием охватываются отдельные функциональные ...

0 комментариев