Математическое моделирование производственной деятельности

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

НОУ "Московский институт управления"

Кафедра: Экономики и управления

Специальность: Экономика и управление на предприятии (в природопользовании)

Форма обучения: заочная

РАБОТА ПО ПРОЙДЕННОМУ КУРСУ

По дисциплине: "АНАЛИЗ И ДИАГНОСТИКА ФИНАНСОВО-ХОЗЯЙСТВЕННОЙ ДЕЯТЕЛЬНОСТИ ПРЕДПРИЯТИЯ "

Тема: "Математическое моделирование производственной деятельности"

студента учебной группы

Мельников Дмитрий Александрович

Руководитель:

МОСКВА 2010 г.

Содержание

Введение

Глава 1. Что такое математическое моделирование?

1.1 Основные этапы математического моделирования

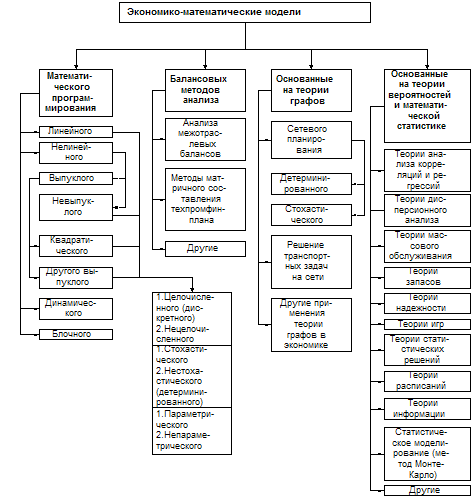
1.2 Классификация моделей

Глава 2. Моделирование экономических процессов

2.1 Моделирование экономических процессов

2.2 Этапы исследования экономических процессов

2.3 Системные предпосылки формирования модели системы управления маркетинговой деятельностью предприятия сферы услуг

Заключение

Используемая литература

Введение

Важными задачами совершенствования производственно-экономических систем (ПЭС) являются повышение эффективности функционирования экономических объектов и достижение высоких конечных результатов деятельности на основе рационального использования производственных ресурсов.

В этом аспекте актуальными являются проблемы оценки эффективности использования ресурсов и функционирования экономических систем различных уровней и масштабов: от отраслевых производственно-хозяйственных комплексов федерального и регионального уровня, до первичных звеньев экономики - промышленных объединений и предприятий.

Решение этих проблем должно опираться на комплексный анализ функционирования производственно-экономических систем, идентификацию характеристик протекающих процессов. Результаты решения таких задач востребованы практикой совершенствования процессов управления производственно-хозяйственной деятельностью объектов экономических отношений в условиях становления современных рыночных механизмов. В концептуальном плане решение таких проблем формирует необходимую информацию для принятия и поддержки эффективных управленческих решений.

В целом, построение экономико-математических моделей и математическое моделирование на их основе являются современным научным направлением, позволяющим вскрывать сущность протекающих экономических процессов, эффективно управлять их поведением и анализировать функционирование экономических объектов и систем.

Глава 1. Что такое математическое моделирование?

С середины XX в. в самых различных областях человеческой деятельности стали широко применять математические методы и ЭВМ. Возникли такие новые дисциплины, как "математическая экономика", "математическая химия", "математическая лингвистика" и т.д., изучающие математические модели соответствующих объектов и явлений, а также методы исследования этих моделей.

Математическая модель - это приближенное описание какого-либо класса явлений или объектов реального мира на языке математики. Основная цель моделирования - исследовать эти объекты и предсказать результаты будущих наблюдений. Однако моделирование - это еще и метод познания окружающего мира, дающий возможность управлять им.

Математическое моделирование и связанный с ним компьютерный эксперимент незаменимы в тех случаях, когда натурный эксперимент невозможен или затруднен по тем или иным причинам. Например, нельзя поставить натурный эксперимент в истории, чтобы проверить, "что было бы, если бы..." Невозможно проверить правильность той или иной космологической теории. В принципе возможно, но вряд ли разумно, поставить эксперимент по распространению какой-либо болезни, например чумы, или осуществить ядерный взрыв, чтобы изучить его последствия. Однако все это вполне можно сделать на компьютере, построив предварительно математические модели изучаемых явлений.

1.1 Основные этапы математического моделирования

 

1) Построение модели. На этом этапе задается некоторый "нематематический" объект - явление природы, конструкция, экономический план, производственный процесс и т.д. При этом, как правило, четкое описание ситуации затруднено. Сначала выявляются основные особенности явления и связи между ними на качественном уровне. Затем найденные качественные зависимости формулируются на языке математики, то есть строится математическая модель. Это самая трудная стадия моделирования.

2) Решение математической задачи, к которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и численных методов решения задачи на ЭВМ, при помощи которых результат может быть найден с необходимой точностью и за допустимое время.

3) Интерпретация полученных следствий из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на языке, принятом в данной области.

4) Проверка адекватности модели. На этом этапе выясняется, согласуются ли результаты эксперимента с теоретическими следствиями из модели в пределах определенной точности.

5) Модификация модели. На этом этапе происходит либо усложнение модели, чтобы она была более адекватной действительности, либо ее упрощение ради достижения практически приемлемого решения.

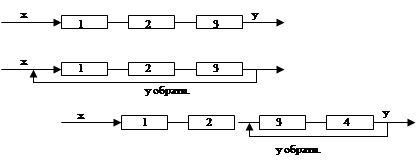
1.2 Классификация моделей

Классифицировать модели можно по разным критериям. Например, по характеру решаемых проблем модели могут быть разделены на функциональные и структурные. В первом случае все величины, характеризующие явление или объект, выражаются количественно. При этом одни из них рассматриваются как независимые переменные, а другие - как функции от этих величин. Математическая модель обычно представляет собой систему уравнений разного типа (дифференциальных, алгебраических и т.д.), устанавливающих количественные зависимости между рассматриваемыми величинами. Во втором случае модель характеризует структуру сложного объекта, состоящего из отдельных частей, между которыми существуют определенные связи. Как правило, эти связи не поддаются количественному измерению. Для построения таких моделей удобно использовать теорию графов. Граф - это математический объект, представляющий собой некоторое множество точек (вершин) на плоскости или в пространстве, некоторые из которых соединены линиями (ребрами).

По характеру исходных данных и результатов предсказания модели могут быть разделены на детерминистические и вероятностно-статистические. Модели первого типа дают определенные, однозначные предсказания. Модели второго типа основаны на статистической информации, а предсказания, полученные с их помощью, имеют вероятностный характер.

Глава 2. Моделирование экономических процессов

В настоящее время одним из наиболее популярных методов исследования бизнес-процессов является имитационное моделирование.

На основе имитационной модели можно построить самые точные и действенные методы анализа и прогнозирования показателей эффективности бизнес-процессов. Тем не менее, нужно быть осторожным и не использовать некорректные процедуры анализа и моделирования, которые могут привести к неточным результатам. В основе имитационной модели лежат понятия потоков, уровней и темпов.

При построении имитационной модели обычно вводят в рассмотрение три потока [96]:

информационный;

финансовый;

кадровый.

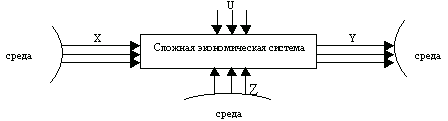
Процедуры построения финансовой, кадровой и информационной маркетинговых систем существенным образом зависят от специфики конкретного предприятия и в обобщенном виде могут быть представлены в виде системы дифференциальных уравнений, связывающих основные уровни и темпы (скорости изменения уровней системы):

где:

вектор уровней системы, построение которого, по словам К. Шеннона [103], является скорее искусством;

матрица темпов.

известная вектор-функция внешних детерминированных воздействия, например инвестиций.

случайные воздействия на систему. Обычно предполагается, чтослучайный Марковский процесс (белый шум) с известными вероятностными характеристиками.

Цель моделирования экономических процессов, как правило, состоит в получении устойчивой схемы, поскольку последовательность оказываемых услуг повторяется. Важной процедурной концепцией анализа эффективности и обеспечения качества управления является определение периода неустойчивой работы и устранение искажения, вносимого статистическими данными, собранными за такой период. При реализации имитационной модели на компьютере дифференциальные уравнения заменяются конечно-разностными, и, именно такие уравнения используются в различных имитационных моделях.

где:

- шаг моделирования;

- матрица темпов увеличения, с индексом “-” матрица темпов уменьшения;

- внешние воздействия;

- случайные возмущения.

 

2.1 Моделирование экономических процессов

Имитационные модели, как об этом уже говорилось, воспроизводят поведение системы на протяжении некоторого промежутка времени. Это достигается путем идентификации ряда событий, распределение которых во времени дает важную информацию о поведении системы. После того как такие события определены, требуемые характеристики системы необходимо регистрировать только в моменты реализации этих событий. Информация о характеристиках системы накапливается в виде статистических данных таких наблюдений. Эта информация обновляется всякий раз при наступлении каждого из интересующих нас событий. Для построения имитационных моделей не требуется использования математических функций, явным образом связывающих те или иные переменные. Эти модели позволяют имитировать поведение сложных систем, для которых построение математических моделей и получение решений невозможно. Более того, гибкость, присущая имитационным моделям, позволяет добиться более точного представления системы. Основной недостаток имитационного моделирования заключается в том, что его реализация эквивалентна проведению множества экспериментов, а это неизбежно обусловливает наличие экспериментальных ошибок. Кроме того, сам процесс оптимизации также вызывает затруднения.

При подготовке к моделированию экономических процессов широко используются так называемые “эвристические методы” и методы экспертных оценок. Они базируются на интуитивно или эмпирически выбираемых правилах, которые позволяют улучшить уже имеющееся решение. Используются в том случае, когда соответствующие математические построения оказываются настолько сложными, что точное решение сформулированной задачи найти нельзя. По существу, эвристические методы представляют собой процедуры поиска разумного перехода от одной точки пространства решений к некоторой другой точке с целью улучшения текущего значения целевой функции модели. Когда дальнейшего приближения к оптимуму добиться невозможно, лучшее из полученных решений принимается в качестве приближенного решения оптимизационной задачи.

Модели экономических процессов разрабатываются с целью оптимизации заданной целевой функции при некоторой совокупности ограничений. Термин “оптимизация” обычно используется для обозначения процессов максимизации или минимизации целевой функции. Поэтому для одной и той же задачи можно предложить две различные модели с различными критериями оптимизации. Например, мы можем предпочесть максимизировать прибыль, или с не меньшим основанием исходить из другой целевой установки - минимизации затрат. Эти критерии не эквивалентны, так как величина затрат может быть функцией переменных, находящихся под контролем данной фирмы, тогда как величина прибыли зависит от внешних неуправляемых факторов, например от ситуации на рынке сбыта, складывающейся под влиянием конкурентов. Использование соответствующих этим критериям оптимизационных моделей при одинаковых ограничениях не обязательно приведет к получению одинаковых оптимальных решений.

Основной вывод, который следует из вышеизложенного, заключается в том, что полученное с помощью некоторой модели конкретное оптимальное решение является наилучшим только в рамках использования именно этой модели. Другими словами, оно является наилучшим из всех возможных только тогда, когда выбранный критерий оптимизации можно считать полностью адекватным целям организации, в которой возникла исследуемая проблемная ситуация. В этом контексте, обеспечение качества управления маркетингом предприятия обеспечивается точностью соответствия модели реальной системе, так как только выводы, получаемые в результате моделирования могут быть применены к реальной системе.

Любая модель экономической системы независимо от ее сложности и адекватности системе-оригиналу принесет мало пользы при отсутствии необходимой информации.

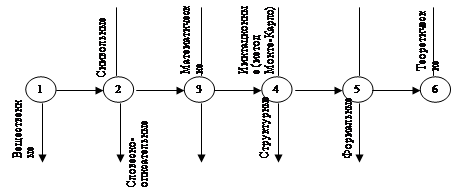
2.2 Этапы исследования экономических процессов

Работа, выполняемая в процессе исследования, состоит из следующих этапов:

1) идентификации проблемы;

2) построения модели;

3) решения поставленной задачи с помощью модели;

4) проверки адекватности модели;

5) реализации результатов исследования.

Хотя эта последовательность не обязательна, ее считают общепринятой.

За исключением этапа, связанного с получением решения на основе разработанной модели, когда используются формализованные методы (линейное программирование, управление запасами, теория массового обслуживания, календарное планирование и т.д.), все остальные этапы исследования выполняются без строгой ориентации на какие-либо регламентирующие правила.

На первом этапе задача исследования заключается в идентификации проблемы. Здесь можно выделить следующие основные стадии:

формулировка задачи или цели исследования,

выявление возможных альтернатив решения применительно к исследуемой ситуации,

определение присущих исследуемой системе требований, условий и ограничений.

Второй этап связан с построением модели. На этом этапе выбирается модель, наиболее подходящая для адекватного описания исследуемой системы. При построении такой модели должны быть установлены количественные соотношения для выражения целевой функции и ограничений в виде функций от управляемых переменных. Если разработанная модель соответствует некоторому общему классу математических моделей экономических процессов (например, моделям линейного программирования или календарного программирования), то для получения решения нужно воспользоваться известными математическими методами. Если же математические соотношения слишком сложны и не позволяют получить аналитического решения задачи, более подходящей для исследования может оказаться имитационная модель. В некоторых случаях возникает необходимость совместного использования математических, имитационных и эвристических моделей. Это все зависит от характерных особенностей и сложности исследуемой задачи.

На третьем этапе осуществляется решение сформулированной задачи. При использовании математической модели решение получают с помощью апробированных оптимизационных методов; при этом модель приводит к оптимальному решению задачи. В случае применения имитационных или эвристических моделей понятие оптимальности становится менее определенным и получаемое решение соответствует лишь приближенным оценкам критериев оптимальности функционирования экономической системы.

На данном этапе кроме нахождения решения всякий раз, когда это возможно, должно быть обеспечено также получение дополнительной информации о возможных изменениях решения при изменение параметров системы. Эту часть исследования называют анализом модели на чувствительность. Он необходим, например, в тех случаях, когда некоторые характеристики исследуемой системы не поддаются точной оценке. В такой ситуации весьма важно исследовать возможные изменения оптимального решения в зависимости от соответствующих параметров системы в некоторых интервалах их количественных значений.

Четвертый этап заключается в проверке адекватности модели. Модель можно считать адекватной, если, несмотря на некоторые неточности отображения системы-оригинала, она способна обеспечить достаточно надежное предсказание поведения системы. Общий метод проверки адекватности модели состоит в сопоставлении получаемых результатов с характеристиками системы. Если при аналогичных входных параметрах модель достаточно точно воспроизводит поведение системы-оригинала, то она считается адекватной. Однако такое сопоставление не дает полной уверенности в том, что поведение системы в предстоящем периоде будет таким же, как в прошлом. А поскольку построение модели осуществляется с использованием ретроспективных данных, то благоприятный исход такого сравнения во многом предопределен. В отдельных случаях, когда система-оригинал исследуется с помощью математической модели, допустима параллельная разработка имитационной модели, предназначенной для проверки основной математической модели.

Заключительный пятый этап связан с реализацией полученных результатов. На данном этапе необходимо оформить конечные результаты исследования в виде детальных инструкций, которые должны быть составлены таким образом, чтобы они легко воспринимались лицами, ответственными за управление экономической системой (службой) и обеспечение ее функционирования.

В основе моделирования экономического процесса лежит работающая модель, копирующая текущую деятельность промышленного предприятия. Это достигается путем прохождения через возможные события в режиме сжатого времени с одновременным отображением хозяйственной деятельности в цифрах. Так как программное обеспечение, реализующее имитационную модель бизнес-процессов, отслеживает статистические параметры ее элементов, оценка эффективности процесса и обеспечение качества управления может быть получена только на основе анализа соответствующих выходных данных.

Составление бюджета продаж услуг должно происходить параллельно с выбором производственной программы предприятия. Только в этом случае можно получить наиболее реальный объем продаж услуг, учитывающий совокупность следующих показателей:

прогнозируемый спрос клиентов;

производственные мощности с учетом остановок производства;

предложение смежников.

Порядок организации и выполнения работ по планированию производства внутри подразделений, включая распределение составляющих услуги, кроме организующих управленческих воздействий содержит достаточно сложный и трудоемкий расчет. Это диктует необходимость разработки программного обеспечения для принятия объективных решений в области управления производственным процессом предприятия.

Для расчета производственной программы вся продукция предприятия подразделяется на следующие типы, отличающиеся друг от друга принципом определения объема производства:

а) продукт (услуга) - объем его выпуска зависит исключительно от внешнего спроса и производственная программа формируется на основе поиска точки равенства спроса и предложения (мощности по продукту);

б) покупной полуфабрикат услуги - объем его выпуска зависит не только от внешнего спроса, но и от внутренней потребности, т.к он используется для производства продукции предприятия. При превышении величины совокупного спроса над предложением предпочтение отдается удовлетворению внешнего спроса, а недостаток по внутренней потребности компенсируется закупкой у поставщиков предприятия;

в) сопутствующие услуги - объем их выпуска определяется только объемом выпуска базовых услуг, с которыми они связаны через нормы выхода.

Критерии расчета производственной программы. Расчет должен учитывать:

1. Потребность в производстве услуги, включающую следующие составляющие:

1.1 Условно-постоянные потребности - если в прогнозе условно-постоянных затрат имеется спрос на элементы, которые производит само предприятие, то это также должно найти отражение при формировании производственной программы.

1.2 Нормативный прирост запасов - возможен, когда величина нормативных запасов одного месяца возрастает и становится больше аналогичного показателя предыдущего периода. Эта положительная разница выступает причиной увеличения производственной программы для обеспечения нормируемых остатков.

1.3 Ранжированный спрос покупателей и заказчиков - основной фактор определения потребности в производстве. Спрос покупателей и заказчиков ранжируется по индивидуально определенным для каждого предприятия критериям и группируется в иерархическую последовательность его удовлетворения.

1.4 Нормируемые затраты при производстве услуги - определяют внутреннюю кооперацию между подразделениями предприятия (потребность в полуфабрикатах собственного производства).

2. Возможности по удовлетворению потребностей в продукции предприятия (услуга) складывается из следующих составляющих:

2.1 Сверхнормативные запасы - показывают излишки готовой к реализации, но нереализованной услуги.

2.2 Собственные мощности - характеризуют производственные возможности предприятия:

Альтернативное использование мощностей - определяет перечень взаимозависимых услуг (как правило, конкурирующих между собой), забирая друг у друга производственные мощности.

Потери мощностей при переходе с одной услуги на другую.

Соотношение мощностей “Основная" услуга - “Сопутствующая” услуга - показывает взаимосвязь между услугами, а также зависимость выработки сопутствующего продукта при производстве основного.