В.Ф.Чаплыгин
Анализ результатов приемных экзаменов в университет, опыт работы со школьниками, слушателями подготовительных отделений, студентами-математиками, готовящими себя к педагогической деятельности, дают основания сделать вывод о том, что при решении текстовых задач учащиеся испытывают значительно больше трудностей, чем при решении уравнений и неравенств. Это отчасти объясняется тем, что для решения уравнений, неравенств или их систем можно использовать некоторый набор известных алгоритмов и приемов, так как сама задача уже формализована, математизирована. А для текстовой задачи математическую модель учащийся должен составить самостоятельно. И поэтому эти задачи, в том числе геометрические, о которых пойдет речь, требуют существенно больших логических усилий. Мы коснемся здесь, в основном, задач на вычисление.
Решение более или менее серьезной задачи требует, во-первых, тщательного ее анализа. Учащийся должен ясно осознать, что же ему известно, как связаны между собой данные величины, какие следствия из них можно получить, что необходимо найти в задаче и что требуется для этого знать. Анализ при этом может носить не только однонаправленный характер (от данных величин к искомым или наоборот), но и встречный, когда движение совершается в двух противоположных направлениях.
Трудным моментом является выбор метода, который приведет к решению задачи наикратчайшим путем. Он, как правило, не однозначен и почти каждая задача допускает не одно решение (имеется в виду не результат, а процесс). Рассуждения, используемые для решения, могут быть чисто геометрические или позаимствованные из алгебры или тригонометрии. К сожалению, приходится констатировать слабые знания учащимися простейших утверждений, фактов, формул. Они затрудняются в измерении углов, связанных с окружностью (вписанных, центральных, составленных хордой и касательной, образованных хордами, пересекающимися внутри окружности, или секущими, исходящими из одной точки вне окружности), не знают свойств касательных и секущих, вписанных и описанных многоугольников, теорем синусов и косинусов, связь значений тригонометрических функций с отношениями сторон прямоугольного треугольника. Хорошо известно, что немаловажную роль в решении геометрических задач имеет чертеж. Если он выполнен верно, то поможет в правильном выборе решения, если ошибочен, то может навести на ложный путь. Говоря об этом, мы не призываем к тому, чтобы включать в курс школьной геометрии как можно больше теорем (на все случаи жизни), а предлагаем создавать комплексы задач, сгруппированных по принципу общих идей или методов решения. Решая задачу, следует обращать внимание учащихся на моменты, помогающие правильно выбрать способ решения, прививать вкус к таким задачам, вселять веру в их творческие возможности, развивать логические способности и интуицию.
Приведем примеры задач, которые нам представляются интересными. Первые три задачи используют подобие.
Задача 1. Прямоугольный треугольник АВС с катетами АС=3, ВС=2 вписан в квадрат. Известно, что вершина А совпадает с вершиной квадрата, а вершины В и С лежат на сторонах квадрата, не содержащих точку А. Найти площадь квадрата.
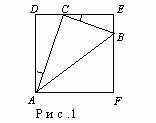В силу равенства отмеченных углов (рис.1) треугольник ACD подобен треугольнику CBE 
. Пусть AD=x, тогда DC=
. Так как AD2+DC2=AC2, то x2+
=9, x2=
. Таким образом, площадь квадрата равна .
Задача 2. На сторонах BC и CD квадрата ABCD выбраны соответственно точки E и F так, что 
и К - точка пересечения отрезков BF и AE. Найти отношение КЕ:АК.
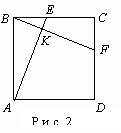Из подобия треугольников (рис.2) AKB, BKE и ABE следует 
. Перемножив равенства 
и 
, получим 
.
Эту задачу можно решить с помощью гомотетии или теоремы Фалеса, но, на наш взгляд, предложенное решение предпочтительнее.
Задача 3. Диаметр окружности с центром О лежит на стороне AD четырехугольника ABCD, при этом АО=ОD. Три остальные стороны АВ, ВС и СD касаются этой окружности. Найти AD, если АВ =а и CD=b.
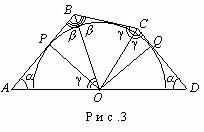Пусть в треугольнике АВО (рис.3) ВАО= , АВО= , ВОА= и, следовательно, + + = . Так как ВО - биссектриса угла СВА, то СВО= .
Если Р и Q - точки касания, то APO= DQO (они прямоугольные, ОР=ОQ, AO=OD) QDO= PAO= . Сумма углов четырехугольника ABCD равна 2 , поэтому С=2 –2 –2 .
А так как СО - биссектриса, то DCO= –( + )= . Таким образом, треугольники АОВ и DCO подобны и 
. Отсюда получаем равенства АО· OD=AB· CD=ab АО=OD=
и AD=2.
А в следующих двух задачах учащиеся должны вспомнить свойства вписанных и описанных четырехугольников.
Задача 4. На стороне ВС параллелограмма ABCD выбрана такая точка Е, что 
=2. Известно, что трапеция AECD обладает следующими свойствами:
1) в нее можно вписать окружность;
2) около нее можно описать окружность.
Найти величину угла BAD.
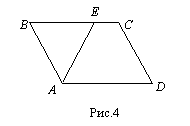В силу свойств, которыми обладает трапеция AECD (рис.4), она равнобокая (АЕ=CD) и 2АЕ=ЕС+AD.
Пусть ВС=3а, тогда BE=2a, EC=a 2AE=EC+AD=4a CD=АЕ=2a.
Таким образом, BEA - равносторонний ABC=60 BAD=120 .
Далеко не все учащиеся могут доказать, почему трапеция, около которой можно описать окружность, является равнобокой.
Задача 5.Сумма углов при основании ВС трапеции ABCD равна 
. Найти величину 
, если известно, что 
=10 и в трапецию ABCD можно вписать окружность.
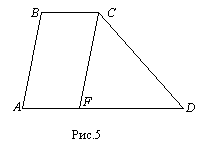Пусть CF AB (рис.5), тогда CF=AB и в силу условия задачи следует,
что FCD=
.
По теореме косинусов
FD2=FC2+СD2-2FC· СDcos (AD–BC)2=AB2+СD2– AB· СD. (1)
Так как в трапецию ABCD можно вписать окружность, то
AD+BC=AB+CD (AD+BC)2=(AB+СD)2. (2)
Разделив равенство (1) на равенство (2), получим
.
Разделив далее числитель и знаменатель левой дроби на произведение AD· BC, а правой части - на AB· СD, получим
.
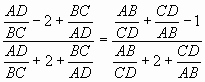Откуда, положив 
=t, и учитывая, что 
=10, имеем t=7.
В этой задаче при неудачном выборе решения оно может оказаться очень громоздким.
Весьма поучительно, на наш взгляд, решение следующей задачи.
Задача 6. В прямоугольном треугольнике АВС из вершины прямого угла С проведена биссектриса CL и медиана СМ. Найти площадь треугольника АВС, если LM=a, CM=b.
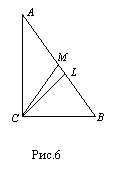Пусть АС=х и ВС=у , где х>y (рис.6), тогда х2+у2=4b2, и по свойству биссектрисы 
LB=
AB=
и, следовательно, ML=MB–LB=b–=
.
Таким образом, приходим к системе
.
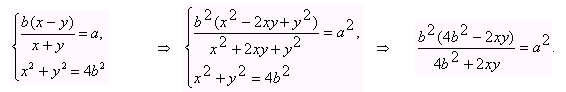Решая это уравнение относительно ху, находим S ABC=
=
.
Следует обратить внимание учащихся на то, что из полученной системы уравнений искать значения переменных х и · у совершенно излишне.
Задача 7. Основание равнобедренного треугольника равно 10 см, проведенная к нему высота - 12 см. Вершины треугольника служат центрами кругов, каждый из которых касается двух других внешним образом. Найти радиусы кругов, которые касаются трех указанных кругов внешним и внутренним образом.
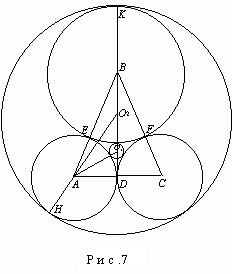Пусть e, f, d, k, h - точки касания, радиус окружности с центром в точке О1 равен r, а с центром в точке О2 - R (рис.7). Так как AD=5, АВ=13,
то BE=8, BО1=8+r, AО1=5+r, О1D=4–r.
Из прямоугольного треугольника AO1D (5+r)2=25+(4–r)2, 18r=16, r=
.
ВО2=R–8, О2D=12–(R–8)=20–R, О2A=R–5,
и, следовательно, из прямоугольного треугольника АО2D имеем
(R–5)2=(20–R)2+25 R=
=13
.
Здесь следует напомнить учащимся, что прямая, проходящая через центры двух касающихся окружностей, проходит через точку их касания.
В заключение приведем одну задачу на доказательство, которая требует от учащихся достаточно высокой логической культуры.
Задача 8. Докажите, что треугольник является равнобедренным в том и только в том случае, когда равны биссектрисы двух внутренних углов.
Если в треугольнике АВС (рис.6) АВ=ВС, то углы А и С равны и равны треугольники ВАЕ и ВСD, так как В - общий и ВАЕ= ВСD, следовательно, АЕ=СD.
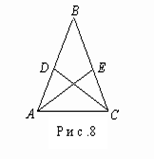Докажем справедливость обратного утверждения. Пусть биссектрисы AE и CD углов А и С треугольника АВС равны. Докажем, что А= С. S АВС=S ВАЕ+S ЕАС 
АВ· АС· sinА=АВ· АЕ· sin
+АЕ· АС· sin
2· АВ· АСcos=(АВ+АС)АЕ АЕ=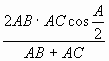
.
Разделив числитель и знаменатель дроби на произведение АВ· АС и обозначив
АВ=с, АС=b, ВС=a, получим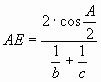 
, аналогично, биссектриса 
.
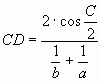Если допустить, что А С, например, А< С, то сos>cos
и а<c 
>
AE>CD, получили противоречие.
Приведенные в статье задачи предлагались на вступительных экзаменах в различных вузах России, в том числе, в Ярославском госуниверситете.
Список литературыПойа Д., Как решать задачу, М.: Учпедгиз,1961,207 с.
Смирнов Е.И., Технология наглядно-модельного обучения математике, Ярославль,1997,323с.
Чаплыгин В.Ф., Чаплыгина Н.Б., Задачи вступительных экзаменов по математике, Ярославль, 1991,140с.
Чаплыгин В.Ф., Чаплыгина Н.Б., Задачи вступительных экзаменов по алгебре и геометрии, Ярославль, 1999,112с.
Сборник задач по математике для поступающих в вузы (под ред. Прилепко А.И.), М.: Высшая школа,1989,271с.
Зафиевский А.В., Вступительные экзамены по математике в 1998году, Ярославль, 1999,36с.
Лидский В.Б., Овсянников Л.В., Тулайков А.Н., Шабунин М.Н., Задачи по элементарной математике, М.: Физматгиз, 1960, 4
Похожие работы
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
... . Следовательно, истинное естественнонаучное и математическое знание ведет, в конечном счете, к установлению подлинно благих правил и норм взаимодействия "разумных агентов". Онтологический статус предметов математики определяется поэтому не их объективной, но их интерсубъективной (См. примечание 5) значимостью. Первоначальная посылка Беркли - "Существовать, значит быть воспринимаемым" - может быть ...
... того материала, который имеется в учебнике, так организовать работу с детьми, чтобы она способствовала развитию пространственного мышления. Глава II. Методика формирования пространственного мышления учащихся основной школы при изучении векторного пространства 2.1 Методические аспекты развития пространственного мышления как элемента образного Рассмотрим, какие подходы предлагают для ...
... . Учитель указывает также примерные сроки проведения зачета. Необходимо отметить, что учащихся, а также их родителей полезно заранее (в начале учебного года) ознакомить со всеми особенностями зачетной системы и условиями проведения зачетов. На специально выделенном уроке проводится зачет. Учащимся предлагается проверочная работа, охватывающая содержание изученной темы. Ее удобно составлять из ...
0 комментариев