Навигация
22.1.1. Запоминающее устройство.
Назначение запоминающего устройства в хранении числовой
информации и передачи ее в другие устройства машины при решении задач.
Емкость запоминающего устройства определяется количеством ячеек
памяти. Каждая ячейка строго фиксирована, и предназначена для хранения
числа или команды программы, называемых обычно машинным словом.
Машинное слово представляет собой совокупность цифр, каждой из которых
соответствует один разряд. Количество разрядов отведенное для записи
одного слова,определяет разрядность машины или так называемая
разрядная сетка. Важной характеристикой ЗУ является время выборки
одного слова информации. При этом под временем выборки понимается
время, необходимое для нахождения слова в общем массиве слов памяти
машины и пересылки его в нужное устройство. Величина времени выборки
непосредственно связана с быстродействием ЦВМ. В современных
вычислительных машинах обычно используются два типа ЗУ: оперативное
запоминающее устройство (ОЗУ) и внешнее запоминающее устройство
(долговременное), (ДЗУ). ОЗУ характеризуется малым временем выборки и
непрерывно используется в процессе вычисления. ДЗУ имеет относительно
большее время выборки, но информации из них используется не
непрерывно, а периодическим путем обмена с ОЗУ, причем этот обмен, как
правило производится большими массивами. Подобное двухступенчатое
построение памяти позволяет хранить большие массивы информации и
быстро ее обрабатывать.
22.1.2. Устройство ввода.
Исходная программа и информация, соответствующим образом закоди-
рованные и перенесенные на материальный носитель информации (перфори-
рованные ленты, перфокарта и т.д.), вводятся в машину при помощи
электронно-механических устройств.
В процессе ввода чтение информации с перфолент, перфокарт, обычно
производится фотосчитывающими устройствами, преобразующими
последовательность отверстий на носителе в последовательность
электрических импульсов.
Общая организация ввода исходной информации и программы состоит
из следующих этапов: нанесение оператором, при помощи клавишных
устройств числовых данных и программы на первичный носитель
информации; контроля подготовленных данных; ввода исходных данных в
вычислительную машину.
При автономной работе входных устройств вводимая информация
поступает в буферное запоминающее устройство, откуда по мере необходи-
мости передается в ОЗУ или ДЗУ.
22.1.3. Устройство вывода.
- 3 -
Устройство вывода предназначено для вывода результатов вычисле-
ний. Организация вывода может быть автономной. В этом случае выводное
устройство работает не синхронно с машиной и выводит информацию из
собственного буферного запоминающего устройства. По мере получения
результатов информация переносится в ОЗУ в буферное ЗУ выходных
устройств, где производится ее обработка и вывод на печать.
22.1.4. Арифметическое устройство.
Арифметическое устройство позволяет осуществить в машине любую
операцию над числами. Оно содержит отдельные блоки для выполнения
различных операций (деления, умножения, сложения и т.д.). Визуальная
индикация результатов выполнения операций позволяет программисту в
процессе отладки программы следить за правильностью выполнения
программы. Полный цикл арифметического устройства складывается из трех
этапов: вывода информации в регистры из ОЗУ, выполнения операции,
передачи результата из регистров в ОЗУ.
22.1.5. Устройство управления.
Устройство управления обеспечивает автоматизацию вычислительных
процессов в соответствии с заданной программой. Программа решения за-
дачи представляет собой определенный набор команд, порядок следования
которых устанавливается заранее при реализации выбранного алгоритма
решения. Каждая команда определяет выполнение одной операции. Это мо-
гут быть операции ввода информации или программы, операции обращения к
запоминающему устройству, арифметические и логические операции, опера-
ции изменения последовательности вычислений (операции перехода).
22.2. Подготовка и решение задач на ЦВМ.
Решение задач на ЦВМ включает следующие этапы: Постановка задачи
- формулирование модели процесса; Математическая формулировка задачи -
составление математического описания; Выбор численных методов решения
управлений; Разработка общего алгоритма; Программирование; Выявление
ошибок (отладка программы); Решение.
_Блок схема последовательности выполнения этапов.
╔═════════════════════════════════════════════════════════════════════╗
║┌──────────────────┐ ┌───────────┐ ┌─────────┐ да ┌─────────────┐║
║│ Выбор численного │ │Составление│ │Проверка ├────>┤Соответствие │║
║│метода и алгоритма├┬─>┤ программы ├─>┤ работы │ нет │ модели │║
║│ решения ││ └───────────┘ │программы├──┐ │ выбранным │║
║└─┬──────────┬─────┘│ └─────────┘ │ │ критериям │║
║ ^ ^ │ ┌─────────────────┐ │ │ оценки │║
║ │ │ └──<─┤Отладка программы├<──────┘ └──┬───────┬──┘║
║ │ │ └─────────────────┘ │ │ ║
║ │ │ нет│ │да ║
║ │ ┌─────┴────────────┐ ┌──────────────────┐ │ │ ║
║ │ │Внесение коренных │ │Внесение изменений├<──────┘ │ ║
║ │ │изменений в метод ├<──┤ в математическое │ │ ║
║ │ │и алгоритм расчета│ │ описание │ │ ║
║ │ └───────────────┬──┘ └──────────────────┘ ┌──────────┴──┐║
╚══╪═══════════════╗ ^ нет │Соответствие │║
┌─┴───────────┐ ║ └──────────────────────────────┤ программы │║
│ Составление │ ╚═════════════════════════════════╗ │ заданным │║
│мат. описания│ ┌───────┐ ┌─────────────────┐ да║ │ критериям │║
└─┬───────────┘ │РЕШЕНИЕ├<────│Разработка модели├<──╫─│эффективности│║
^ └───────┘ │ закончена │ ║ └─────────────┘║
┌─┴───────────┐ └─────────────────┘ ╚════════════════╝
│Постановка │
│ задачи │
└─────────────┘
Блоки обведенные двойной линией, при использовании системы
автоматического регулирования (программирования) могут быть обработаны
машиной автоматически. Естественно, такая должна обладать блоками
синтеза и анализа структур. Формирование модели процесса целиком
является компетенцией исследователя или технолога. Именно на этом
этапе определяется физическое содержание задачи и весь круг явлений,
включенных в рассмотрение. Следует четко представлять цель, которую
- 4 -
необходимо достигнуть при завершении расчетов, а так же возможность
последующей проверки расчетных результатов и их практической
реализации.
Задача составления математического описания процесса наиболее
точно отвечающего реальным условиям его протекания, зависит прежде
всего от степени изученности отдельных составляющих элементов и степе-
ни их взаимосвязи.
Наиболее общим приемам разработки математического описания про-
цесса является блочный принцип. Согласно этому принципу составлению
математического описания предшествует анализ отдельных "элементарных"
процессов, протекающих в объекте моделирования.
В составе математического описания, разработанного на основе фи-
зической природы моделируемого процесса, обычно можно выделить следую-
щие группы уравнений:
Уравнения баланса массы и энергии, записанные с учетом
гидродинамического режима в объекте; эта группа обычно определяет
распределение температуры в потоках, составов и связанных с ними
свойств, например плотности, вязкости и т.д.;
Уравнения элементарных процессов, определяющих изменение
переменных состояния потоков веществ и их взаимодействие. К этой груп-
пе относятся описания процессов химических превращений, массо- и
теплообмена.
Теоретические, полу-эмпирические или эмпирические между различны-
ми параметрами модели, например, зависимость коэффициента массопереда-
чи от скорости потоков фаз, зависимость плотности раствора от состава
и т.д.
Кроме перечисленных выше групп уравнений в состав математического
описания могут входить различные ограничения на допустимые области ис-
пользования теоретических или эмпирических зависимостей, ограничения
на диапазон изменения некоторых из переменных и т.д.
_ 23. Цели и задачи оптимизации технологических систем.
Бурное развитие техники, интенсификация производства,
необходимость увеличения производительности труда выдвинули перед
учеными инженерами работающими в области автоматики, задачи создания
высококачественных систем автоматического управления (САУ), которые
способны решать все более сложные задачи управления и заменить
человека в сложных сферах его деятельности.
Параллельно с развитием техники развивалась техническая киберне-
тика, являющаяся базой современной автоматики и телемеханики. Одним из
важнейших направлений технической кибернетики является теория опти-
мальных автоматических систем, которая зародилась в конце 40-х годов.
Под оптимальной САУ понимается наилучшая в известном смысле
система. Решение проблемы оптимальности позволит довести до максимума
эффективность использования производственных агрегатов, увеличить
производительность и качество продукции, обеспечить экономию энергии и
ценного сырья и т.д. В различных отраслях техники управления
рассмотрения проблем оптимальности систем приводит к задачам
построения оптимальных по быстродействию САУ, оптимальной фильтрации
сигнала принимаемого на фоне помех, построения оптимальных
прогнозирующих устройств, оптимальных методов распознавания образов,
оптимальной организации автоматического поиска и т.д. Между всеми
этими различными на первый взгляд задачами имеется внутренняя связь,
которая является базой для построения единой теории оптимальных
систем.
Критерии оптимальности, на основе которых строится система, могут
быть различны и зависят от специфики решаемой задачи. Это могут быть
простота, экономичность, надежность. Для процессов САУ критериями мо-
гут быть время регулирования, вид кривой переходного процесса, точ-
ность воспроизведения входного сигнала при наличии помех и т.п.
Значение теории оптимальных систем для практики исключительно ве-
лико. Без нее трудно создавать оптимальные САУ. Теория оптимальных
систем позволяет оценить тот предел, который может быть достигнут в
- 5 -
оптимальной системе, сравнить ее с показателями действующей не опти-
мальной системы и выяснить, целесообразно ли в рассматриваемом случае
заниматься разработкой оптимальной системы.
Принципы оптимального управления получают все большее
распространение на практике. Они позволили создать новые
автоматические регуляторы, и достигнуть существенного процесса в их
основных свойствах. Несмотря на полученные результаты ряд важнейших
проблем оптимального управления остается еще не решенным. К ним
относятся проблемы построения систем, близким к оптимальным, синтез
оптимальных управляющих устройств и др.
Оптимизация любого процесса заключается в нахождении оптимума
рассматриваемой функции или соответственно оптимальных условий прове-
дения данного процесса.
Для оценки оптимума необходимо прежде всего выбрать критерии
оптимизации. В зависимости от конкретных условий в качестве критерия
оптимизации можно взять технологический критерий, например,
максимальный съем продукции с единицы объема аппарата; экономический
критерий - минимальная стоимость продукта при заданной
производительности и др.
На основании выбранного критерия оптимизации составляется так
называемая целевая функция или функция выгоды, представляющая собой
зависимость критерия оптимизации от параметров, влияющих на его
значение. Задача оптимизации сводится к нахождению экстремума целевой
функции. Следует иметь в виду, что проблемы оптимизации возникают в
тех случаях, когда необходимо решать компромиссную задачу
преимущественного улучшения двух или более количественных
характеристик, различным образом влияющих на переменные процесса,
балансируя одну против другой. Например, эффективность процесса
балансирует против производительности; качество - против количества;
запас единиц продукции - против реализации их; производительность -
- против затрат и т.д.
Для автоматически управляемого процесса, автоматически управляе-
мой системы, различают две стадии оптимизации: статическую и динами-
ческую.
Статическая оптимизация решает вопросы создания и реализации
оптимальной модели процесса, а динамическая - создание и реализация
системы оптимального управления процессом.
В зависимости от характера рассматриваемых математических моделей
принимаются различные математические методы оптимизации. Все они
сводятся к тому, чтобы найти минимум или максимум, описываемой
уравнением целевой функции.
При выборе метода оптимизации необходимо учитывать могущие
возникнуть вычислительные трудности: объем вычислений, сложность
самого метода, размерность задач и т.п. Целесообразно производить по
возможности предварительные оценки положения оптимума какой-либо
конкретной задачи. Для этого необходимо детально рассмотреть исходные
данные и основные соотношения между переменными. Для сокращения
размерности задачи часто используется прием сведения нескольких
переменных к наиболее существенным.
Целесообразно применение однотипных вычислительных схем. При
использовании вычислительных машин с помощью стандартных подпрограмм
удается упростить расчеты и лишь для целевых функций требуется
создавать специальную программу.
Не представляется возможным изложить твердые правила упрощения
задач для всех возможных случаев; необходимо каждый раз подходить к
выбору метода оптимизации и решению задачи, исходя из конкретного су-
щества самой задачи.
_ 24. Основы системного анализа процессов и аппаратов
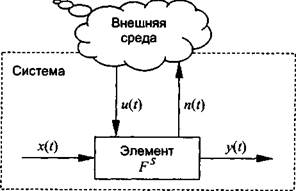
1Системный анализ 0 это методология исследования любых объектов
средством представления их в качестве систем и анализа этих систем.
1Система 0 это совокупность взаимосвязанных элементов, объединенных для
достижения поставленной цели. Для выявления элементов производят де-
- 6 -
композицию системы. 1 Технологическая система - 0 совокупность технологи-
ческих процессов и средств для их реализации.
Любую технологическую систему расчленяют на 4 основных элемента:
1) Собственно технологический процесс.
2) Аппарат для реализации процесса.
3) Средства контроля и управления.
4) Информационные связи между тремя предыдущими подсистемами.
В зависимости от масштабов технологические системы бывают:
1) Малые системы (один типовой процесс, один типовой аппарат).
2) Большие системы - совокупность малых систем.
Процессы в системном анализе бывают 1 детерминированные 0 и 1стохасти-
1ческие. Детерминированные 0 характеризуются однозначной непрерывной за-
висимостью между входными и выходными величинами. при этом каждому
значению входной величины соответствует определенное значение выходной
величины. В 1 стохастических 0 процессах изменение определяющих величин
происходит беспорядочно хаотично и чаще всего дискретно. Значение
выходной величины не находится в соответствии с входной.
24.1. Основные этапы системного анализа.
Этап 1
1.1. Анализ современного состояния объекта. Изучение физико-химических
особенностей, конструктивное и аппаратное оформление системы,
технологических особенностей.
1.2. Средства контроля и управления, технико-экономические и
экологическо-социальные особенности системы.
Этап 2: Постановка задачи оптимизации.
2.1. Формирование исходного числового материала для математического
моделирования (по сырью, реагентам, энергии, сбыту, количеству).
2.2. Формулирование критерия оптимизации.
Этап 3: Выбор математической модели.
3.1. Выбор типовой математической модели.
3.2. Формулирование рабочей гипотезы о работе механизма процесса.
3.3. Принятие допущений, идеализирующих реальную систему. Приведение
модели к окончательному рабочему виду (зависит от средств реализации
ЭВМ).
3.4. Формирование алгоритмов, реализующих математические модели.
Этап 4: Идентификация математической модели.
4.1. Проверка эксперимента.
4.2. Сравнение результатов эксперимента и расчета.
Этап 5: Анализ результатов моделирования.
5.1. Анализ основных связей независимых переменных с входными величи-
нами и критериями оптимизации (анализ статических характеристик).
5.2. Анализ чувствительности возможных критериев оптимизации и отсев
несущественно влияющих связей.
5.3. Анализ допустимых решений задач оптимизации.
5.4. Анализ экономической целесообразности автоматической оптимизации
системы
Этап 6: Уточнение задачи оптимизации.
6.1. Анализ возможности реализации алгоритма оптимизации существующим
математическим обеспечением.
6.2. Формирование алгоритма оптимизации. Составление качественной
оценки контрольного варианта.
1Оптимизация - 0 процедура поиска экстремального значения 1 0 выбранного
критерия при выполнении наложенных ограничений и условий физической
реализуемости.
Этап 7: Анализ результатов эксперимента.
7.1. Выявление свойств оптимальных режимов системы.
7.2. Разработка структуры системы автоматической оптимизации.
7.3. Разработка задания на создание алгоритмов оптимизации,
использующих свойства оптимальных режимов.
Далее разрабатывается эскизный проект, техническое задание и рабочий
проект.
.
- 7 -
_ 25. Список литературы.
1. БояреновА.И., КофаровВ.В. "Методы оптимизации в химической
технологии", М-72, Изд. Наука, 487 стр.
2. КафаровВ.В., "Методы кибернетики в химии и химической технологии",
М-71,"Химия", 496 стр..
Похожие работы
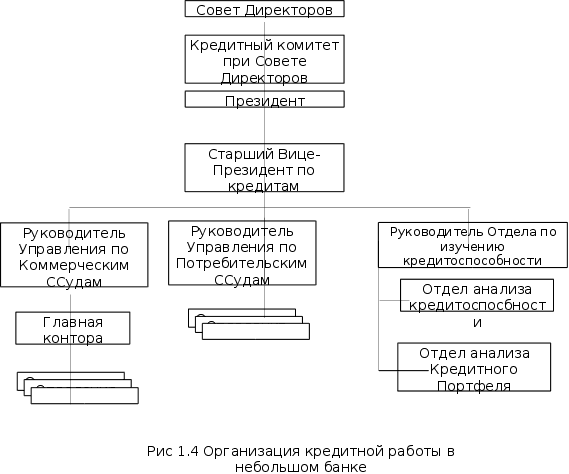
... выявления недостатков и «узких мест» этих систем и подготовке рекомендаций по улучшению функционирования и прогнозированию их развития в условиях информационной неопределенности. Глава 3 Системный анализ управления кредитами.3.1. Анализ кредитных задолженностей в 1995 и 1996 годах. Работа банковской системы любого государства определяется, прежде всего, конечными результатами, представленными в ...
... , динамические и статические, простые и сложные, естественные и искусственные, с управлением и без управления, непрерывные и дискретные, детерминированные и стохастические, открытые и замкнутые. Основы системного анализа Деление систем на физические и абстрактные позволяет различать реальные системы (объекты, явления, процессы) и системы, являющиеся определенными отображениями (моделями) ре ...
... противоположные подходы, но нельзя считать ни один из них "юридически законным" или вытекающим из каких ни будь законов природы, нельзя считать стиль управления системой на основе системного анализа "правильным", "современным", "куль-турным". Другое дело — не знать о возможности применения системного подхода к вопросам управления — вот это неправильно, некультурно. Пример системного подхода ...
... , связанным с планированием. Разные люди используют различные термины для определения одного и того же явления или понятия. Многие руководители пользуются как синонимами терминами «системный анализ», «исследование операций», «операционный анализ». Другие пытаются выделить специальные области исследований, определяемые перечисленными терминами. Если направить свой интерес на понимание смысла и ...
0 комментариев