Навигация
Устройство деления 16-ти разрядных чисел с плавающей запятой
СОДЕРЖАНИЕ
1. Техническое задание......................2
2. Введение.................................3
3. Анализ технического задания..............4
Приложение 1................................7
Приложение 2................................8
Приложение 3................................9
Приложение 4...............................10
Список литературы..........................11
1. ТЕХНИЧЕСКОЕ ЗАДАНИЕ
Разработать устройство деления 16-ти разрядных чисел с плавающей
запятой, где :
ОСНОВНЫЕ ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ:
1.1. Формат входных данных - двоичные числа с плавающей запятой,
представленные в прямом коде
1.2. Длина одного слова 16 бит, где:
- порядок - 7 бит
- знаковая часть - 1 бит
- мантисса - 7 бит
- знаковая часть - 1 бит
1.3. Диапазон представления чисел:
от - 2_а0_А + 2_а-15_А до 2_а0_А - 2_а-15
1.4. Точность представления чисел : 2_а-15
1.5. Обнаружение одиночных ошибок в операции деления.
2. ВВЕДЕНИЕ
В современных ЭВМ один из основных элементов является блок АЛУ(арифметико-логическое устройство), которое осуществляет арифметические и логические операции над поступающими в ЭВМ машинными словами.Важнейшей операцией, выполняемой в АЛУ, является операция деления,которая может проводиться над двоичными числами с фиксированной запятой, двоичными числами с плавающей запятой, десятичными целыми числами и т.д.
В данной курсовой работе деление производится над двоичными числами с плавающей запятой, причем для улучшения надежности и быстродействия данной схемы используются микросхемы, применяемые для создания современных ЭВМ (в том числе и для ЭВМ, создаваемых в НПО "Персей").
3. АНАЛИЗ ТЕХНИЧЕСКОГО ЗАДАНИЯ
3.1. Техническое задание представляет собой задачу создания устройства деления для 16-ти разрядных чисел с плавающей запятой с обнаружением ошибок.
В ЭВМ числа с плавающей запятой в общем случае представляются ввиде:
X = S_рp_Аg ; g < 1,
где: g - мантисса числа X; S_аp_А - характеристика числа X; p - порядок; S - основание характеристики.
Обычно число S совпадает с основанием мантиссы g. Мантисса g правильная дробь. Порядок p, который можнт быть положительным или отрицательнымчислом, определяет положение запятой в числе X.
Для двоичных чисел число с плавающей запятой имеет вид:
X = 2_рp_Аg ; g < 1,
Структурно двоичное число с плавающей запятой в ЭВМ представленона рис. 1. в Приложении 1.
3.2. ДЕЛЕНИЕ КАК АРИФМЕТИЧЕСКОЕ ДЕЙСТВИЕ В ЭВМ
3.2.1. В ЭВМ для выполнения арифметических и логических преобразований служит арифметическо-логические устройства (АЛУ). Преобразования над операндами (словами) представляют собой сложение, вычитание, вычитание модулей, умножение и деление. Это арифметические операции. Группу логических операций составляют операциидизъюнкции и конъюнкции. Специальные арифметические операции включают нормализацию, арифметический сдвиг, логический сдвиг.
По способу представления чисел различают следующие типв АЛУ:
- для чисел с фиксированной запятой; - для чисел с плавающей запятой; - для десятичных чисел.
3.2.2. Деление чисел с плавающей запятой выполняется в соответствии с формулой:
X S_аpx_Аgx gx --- = ------ = S_аp_АX_а-py_А --- Y S_аpy_Аgy gy .
При делении чисел с плавающей запятой мантисса частного равначастному от деления мантиссы делимого на мантиссу делителя, а порядокчастного - разности порядков делимого и делителя. Частное нормализуется и ему присваивается знак "плюс", если делимое и делитель имеютодинаковые знаки ; и знак "минус", если делимое и делитель имеют разные знаки.
3.2.3. Таким образом нахождение частного сводится к выполнениютрех операций:
- определение знака частного; - определение порядка частного; - определение мантиссы частного.
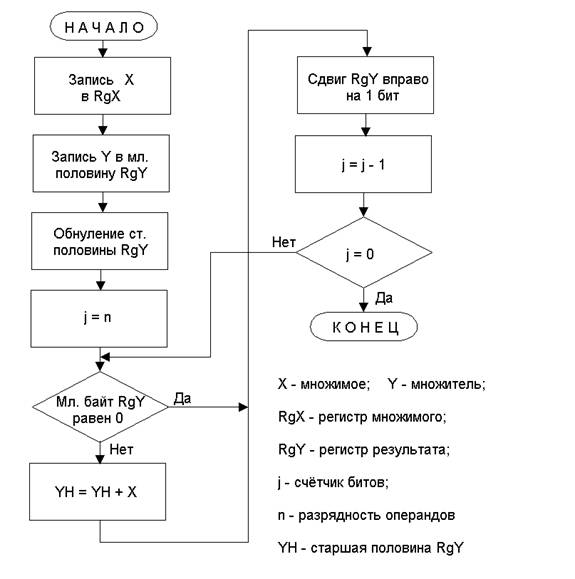
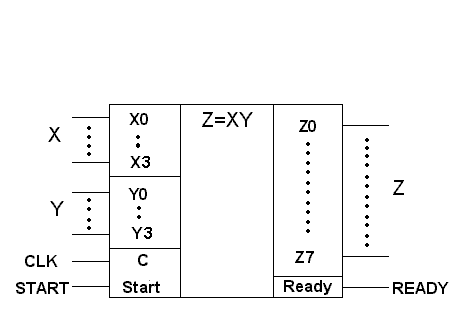
Структурно все эти операции представлены на рис.2 в Приложении 1.
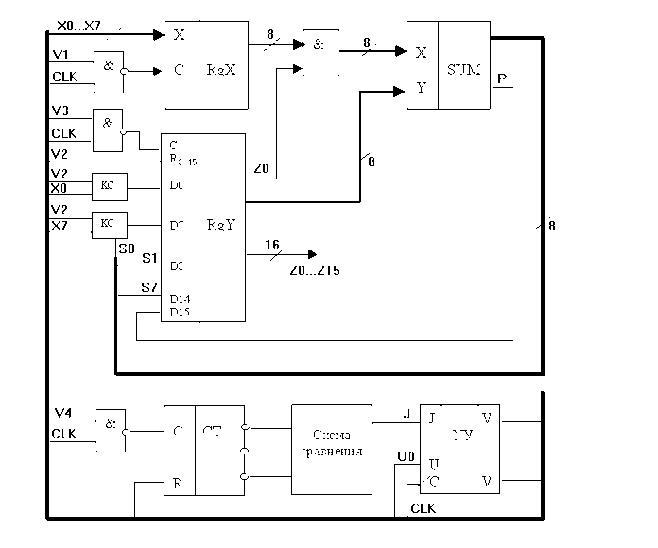
В соответствии с техническим заданием, необходимо проводить контроль над конечным результатом, т.е. обнаружить одиночную ошибку. Дляданного задания обнаружение одиночной ошибки производится методомсравнения. Структурная схема разработанного устройства показана на рис. 2-ав Приложении 2.
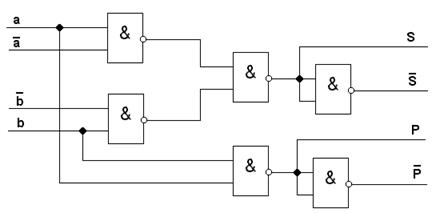
3.2.4. БЛОК ОПРЕДЕЛЕНИЯ ЗНАКА ЧАСТНОГО
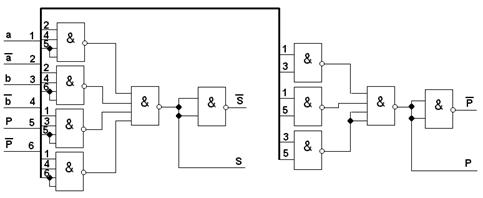
В соответствии с Рис.1 в Приложении 1 знаки порядка и мантиссычастного будут зависеть от одноименности или разноименности знаковпорядков и мантисс делимого и делителя. Однако знаки порядка и мантиссы частного определяются по-разному. А именно: -- Для определения знака мантиссы частного рассмотрен двухтактный счетчик (рис.3 в Приложении 1.). При поступлении информации счи таетсч, что комбинация одноименных значений (00 или 11) дает ко нечную информацию -"0" (т.е. "+" или "отсутствие знака"). В про тивном случае информация - "1" (т.е. "-" или "наличие знака"). Организуются 2 такта работы. -- Определение знака порядка производится с помощью сложения по модулю 2. Этот элемент схемы входит в блок определения порядка частного (см. рис.4 в Приложении 3.). Наличие знака дает инфор мацию по прямому выходу (это есть"1"), в противном случае инвер сный выход дает информацию "0".
Похожие работы
... характер сигналов интерфейса и их временную диаграмму, а также описание электрофизических параметров сигналов. На рис. 2.2 представлена общая схема сопряжения МП с устройствами ввода-вывода УВВ и ОЗУ в микропроцессорной системе. Рис 2.2. Схема интерфейсных связей микропроцессора Связь МП с УВВ требует пять групп связей, обеспечиваемых через выводы корпуса МП. По группе шин 1 передается ...
... этих кодов операция вычитания (или алгебраического сложения) сводится к арифметическому сложению. В результате упрощаются арифметические устройства машин. Для представления двоичных чисел в машине применяют прямой, обратный и дополнительный коды. Во всех этих кодах предусматривается дополнительный разряд для представления знака числа, причем знак «+» кодируется цифрой 0, а знак « — » - цифрой 1. ...
... RgХ и RgY имеют как прямые, так и инверсные выходы , что позволяет уменьшить количество элементов в сумматоре. Рисунок 2.2 Структурная схема АЛУ для умножения двоичных чисел. Как видно из схемы активный уровень сигналов управления - высокий, и устройство управления тактируется по фронту импульса, а исполнительные устройства - по спаду, что позволяет избежать гонок в схеме. 3 Синтез ...
... 100 10 1001=(9)10 100 11,1=(3,5)10 00 110 00 100 001 100 000 100 10 0 10 00 Таким образом, выполнение арифметических операций в двоичной системе счисления достаточно просто. Особенно просто выполнять операции сложения, вычитания и умножения. Благодоря этому, применение двоичной системы в вычислительных ...



0 комментариев