Навигация
БЛОК ОПРЕДЕЛЕНИЯ ПОРЯДКА ЧАСТНОГО (рис.4 в Приложении 3)
3.2.5. БЛОК ОПРЕДЕЛЕНИЯ ПОРЯДКА ЧАСТНОГО (рис.4 в Приложении 3).
Определение порядка сводится к "вычитанию" порядков делимого иделителя. Порядки операндов и их знаки поступают в регистры Рг.1,Рг.2, Зн.Рг.1 и Зн.Рг.2 соответственно. Затем в сумматоре происходит"вычитание", т.е. сложение порядка делимого и делителя. Причем порядок делителя представлен в дополнительном коде. После этого вся информация поступает в регистр результата Рг.Р.
3.5.6. ОБНАРУЖЕНИЕ ОДИНОЧНОЙ ОШИБКИ
Для этой цели используется поразрядное сравнение основной и дублирующей информации по модулю 2. Несовпадение информации выдает "0"или ошибку.(См. рис.2-а в Приложении 2).
Приложение 1.
┌────────────────────┐
│Магистраль операндов│
└──────────┬─────────┘
┌───────────────┬─────────┴────┬───────────────┐
┌──┴───┐ ┌─────┴─────┐ ┌───┴───┐ ┌──────┴─────┐
│Знак Р│ │Порядок (Р)│ │Знак m │ │Мантисса (m)│
└──────┘ └───────────┘ └───────┘ └────────────┘
Рис. 1. Представление двоичного числа
с плавающей запятой.
┌──────────────────┬─────────────────┬──────────────────┐
│Блок определения │ Блок │ Блок │
│ знака числа │ определения │ определения │
├────────┬─────────┤ порядка частного│ мантиссы частного│
│Знак │ Знак │ │ │
│порядка │ мантиссы│ │ │
└────────┴─────────┴─────────────────┴──────────────────┘
Рис. 2. Нахождение частного.
│
│
│
│
┌───────────┐ ┌──────┴──────┐
──────┤ 1 │ │ & │
│ ├──────┤ │
──────┤ │ │ │
└───────────┘ └──────┬──────┘
│
│
┌─────────────┐
│ │
│ Счетчик │
│ │
└─────────────┘
Рис. 3. Блок определения знака мантиссы
частного с помощью двухтактового
счетчика.
Приложение 2.
Магистраль
┌─────────────────────────────
│
│
┌─────────────┴─────────────┐
│ │
│ │
┌────────┴────────┐ ┌───────┴────────┐
│ │ │ │
│ УД │ │ УДg │
│ │ │ │
│ (Устройство де-│ │ (Устройство де-│
│ления) │ │ления дублиру-│
│ │ │ющее) │
│ │ │ │
└────────┬────────┘ └────────┬───────┘
│ │
│ 16 │ 16
│ │
├──┴────────────────────────────┼────┤
│
│
├───────────────────────────────┴────┤
┌────────────────────────────────────┐
│ │
│ mod 2 │
│ │
└─────────────────┬──────────────────┘
│
│
│ 16
│
├─────────────────┼──────────────────┤
│
│
┌─────────────────┴──────────────────┐
│ 1 │
│ │
│ │
│ │
└─────────────────┬──────────────────┘
│
│
│ Сигнал ошибки "1"
Рис. 2-а. Структурная схема устройства деления
с обнаружением одиночных ошибок.
Приложение 3.
Магистраль операндов
────────────┬─────┬─────
│ │
┌────┼─────┴───────────────┐
│ │ │
│ │ │
┌────────────────┼────┴───────┐ │
│ │ │ │
┌────┴───┐ │ ┌────┴───┐ │
│Зн.Рг.1 │ │ │Зн.Рг.2 │ │
└──┬─────┘ │ └───┬────┘ │
│ │ │ │
│ ┌────┴───┐ │ ┌────┴───┐
│ │ Рг.1 │ │ │ Рг.2 │
│ └────┬───┘ │ └─┬────o─┘
│ │ │ │ │
│ │ │ │ │
│ ┌───────────┼───────────┘ │ │
│ │ │ │ │
┌──┴──────┴───┐ │ ┌──────────├───┴────┼────┤
│ mod 2 │ │ │ ├────────┴────┤─┐
│ │ │ │ ┌─────────────┐ │
└──┬──────o───┘ │ │ │ 1 │ │
│ │ │ │ │ │ │
│ │ │ │ └───────┬─────┘ │
│ └───────────┼────────┘ │ │
│ │ ┌─────────────────┘ │
│ │ │ │
└──────────────────┼─────────┼─────────────────────────┘
│ │
─────┴─── ───┴─────
СМ
──────┬───────
│
│
┌──────────┴───────────┐
│ Рг. Р. │
│ │
└──────────┬───────────┘
│
│
o
Рис. 4. Определение порядка частного и его
знака (mod 2).
Приложение 4.
│ Магистраль
┌─────────────┐ ┌───────────┴───────────────────┐
│ │ │ ┌───┴────────────┐
│ ├────────┼──┴──────┤ │ Рг. д-ль │
│ ┌─┼────────┴─────────┤ └───o────────────┘
│ │ │
│ │ ───────────────── │
│ │ Рг. р. Р. │
│ │ ──────────────┬── │
│ │ │ │
│ │ │ │
│ │ │ │
│ │ ─────┴──────────── ────────────┴─────
│ │ +"1"
│ │ СМ ─────
│ │
│ │ ──────┬──────────┬────────────────
│ │ ┌──────┘ │
│ │ │ ┌──────┴───────┐
│ │ │ │ Рг. Р. │
│ │ │ Р └──────┬───────┘
└──┼────────────┼─────────────────┘
│ │
│ ┌──────┴──────┐
│ │ Тг. │
│ │ │
│ └──┬──────o───┘ ─────────────────
│ │ │ Рг.
│ │ │ ┌────────────────
│ └──────┼────────────────┤
│ │
└───────────────┘
Рис. 5. Блок определения мантиссы частного.
СПИСОК ЛИТЕРАТУРЫ
1. Коган Б.М. "Электронные вычислительные машины и системы",
М. 1979г.
2. Граф Ш., Гессель М., "Схемы поиска неисправностей",
М. 1989г.
МОСКОВСКИЙ ИНСТИТУТ РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И АВТОМАТИКИ
ВЕЧЕРНИЙ ФАКУЛЬТЕТ
ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
КУРСОВАЯ РАБОТА
по курсу
ПРИКЛАДНАЯ ТЕОРИЯ ЦИФРОВЫХ АВТОМАТОВ
Студент гр. ВСЦ-12-91
Крючков Дмитрий
МОСКВА 19
Похожие работы
... характер сигналов интерфейса и их временную диаграмму, а также описание электрофизических параметров сигналов. На рис. 2.2 представлена общая схема сопряжения МП с устройствами ввода-вывода УВВ и ОЗУ в микропроцессорной системе. Рис 2.2. Схема интерфейсных связей микропроцессора Связь МП с УВВ требует пять групп связей, обеспечиваемых через выводы корпуса МП. По группе шин 1 передается ...
... этих кодов операция вычитания (или алгебраического сложения) сводится к арифметическому сложению. В результате упрощаются арифметические устройства машин. Для представления двоичных чисел в машине применяют прямой, обратный и дополнительный коды. Во всех этих кодах предусматривается дополнительный разряд для представления знака числа, причем знак «+» кодируется цифрой 0, а знак « — » - цифрой 1. ...
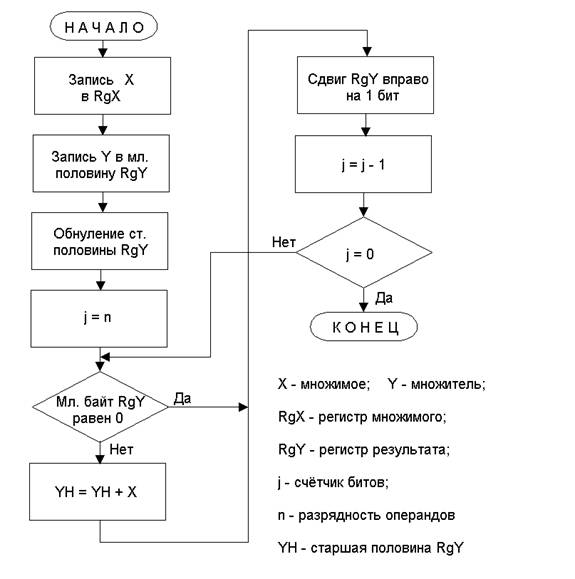
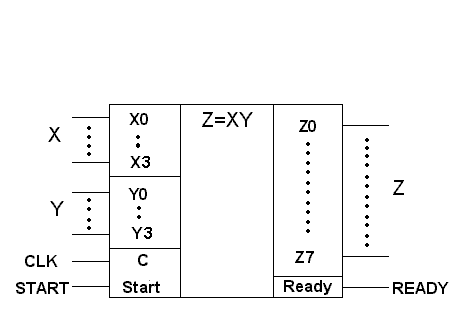
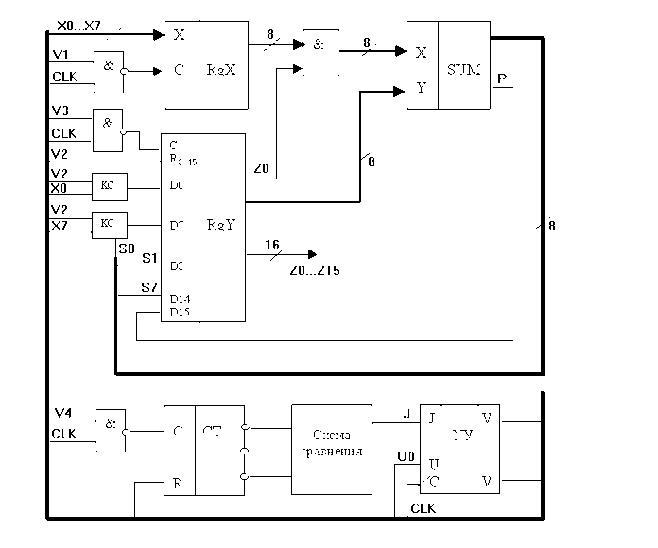
... RgХ и RgY имеют как прямые, так и инверсные выходы , что позволяет уменьшить количество элементов в сумматоре. Рисунок 2.2 Структурная схема АЛУ для умножения двоичных чисел. Как видно из схемы активный уровень сигналов управления - высокий, и устройство управления тактируется по фронту импульса, а исполнительные устройства - по спаду, что позволяет избежать гонок в схеме. 3 Синтез ...
... 100 10 1001=(9)10 100 11,1=(3,5)10 00 110 00 100 001 100 000 100 10 0 10 00 Таким образом, выполнение арифметических операций в двоичной системе счисления достаточно просто. Особенно просто выполнять операции сложения, вычитания и умножения. Благодоря этому, применение двоичной системы в вычислительных ...



0 комментариев