Навигация
2.1. Вычисление определителей
Пусть имеем квадратную матрицу размером n´ n:
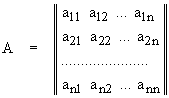 . (2.1.1)
. (2.1.1)
Требуется вычислить определитель матрицы det(A).
Эквивалентным преобразованием матрицы называют преобразования матрицы, не изменяющие величину определителя матрицы. Эквивалентным является следующее преобразование: любую строку матрицы можно заме-нить суммой исходной строки и любой другой, умноженной на любое число, не равное нулю.
Используя такого рода преобразования можно попытаться привести ис-ходную матрицу к треугольному виду:
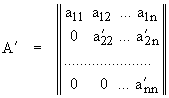 ,
,
при этом det(A) = det(A¢ ).
Формула для пересчета элементов матрицы имеет вид:
![]() , (2.1.2)
, (2.1.2)
гдеi- номер столбца, в котором элементы, лежащие ниже главной
диагонали, превращаются в нули;
j- номер элемента в обрабатываемом столбце (т.е. номер строки);
k- номер элемента в текущей строке.
Алгоритм приведения матрицы к треугольному виду включает в себя 3 вложенных цикла:
- внешний цикл, i = 1 .. n-1 ;
- средний цикл, j = i+1 .. n ;
- внутренний цикл, k = i+1 .. n .
Теперь искомый определитель вычисляется как произведение диагональных элементов:
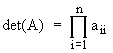 .
.
Описанный выше алгоритм дает результат не всегда. Если при выполнении i-того шага внешнего цикла диагональный элемент aii оказывается равным нулю, а среди элементов i-того столбца с номерами от i+1 до n есть хотя бы один не нулевой, алгоритм завершается безрезультатно (из-за невозможности вычислений по формуле (2.1.2). Для того, чтобы это не происходило, используется прием, который называется “выбор главного элемента”.
При выполнении очередного шага цикла по i предварительно выполняются следующие операции:
1) находится максимальный по модулю элемент среди элементов i-того столбца от aii до ani ;
2) если найденный элемент ali равен нулю, процесс вычисления завершается с выдачей результата det(A) = 0 ;
3) если l¹ i , тогда строки исходной матрицы с номерами i,l поменять местами.
После завершения преобразования матрицы, определитель вычисляется по формуле:
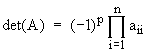 ,
,
где p – число выполненных операций перемены строк местами.
2.2 Обращение матриц
Обратной к матрице A называется матрица A-1, обладающая свойством:
A× A-1 = A-1× A = I ,
где I – единичная диагональная матрица. Опишем один из универсальных и эффективных методов расчета обратной матрицы (метод Жордана-Гаусса, в книге [4-218] описан как “метод исключений”). В [5-22] приведен более эффективный по памяти алгоритм обращения матрицы.
Пусть имеем матрицу A вида (2.1.1) и пусть B – единичная диагональная матрица такого же размера. Создадим рабочую матрицу R размером N´ 2N просто присоединив матрицу B справа к матрице A :
 .
.
Над строками такой расширенной матрицы будем производить преобразования, аналогичные тем, которые были описаны в п.2.1. Левую часть матрицы R будем называть подматрицей A, правую – подматрицей B. Весь процесс преобразования матрицы R разобьем на 3 этапа.
1 этап. Выполним преобразования строк матрицы так, чтобы все элементы, лежащие ниже диагональных элементов подматрицы A, обратились в нули. При этом может использоваться выбор главного элемента.
2 этап. Выполним преобразования так, чтобы все элементы, лежащие выше диагональных элементов подматрицы A, обратились в нули. Преобразования надо выполнять в обратном порядке: со столбца номер n и до столбца номер 2.
3 этап. Каждую строку расширенной матрицы R с номером i делим на диагональный элемент aii .
После завершения процедуры подматрица A превращается в единичную диагональную матрицу, а подматрица B будет равна искомой обратной матрице A-1 . Алгоритм имеет порядок O(n3).
2.3. Методы решения систем линейных уравнений
Задача поиска решений системы линейных уравнений имеет не только самостоятельное значение, но часто является составной частью алгоритма решения многих нелинейных задач. Основные методы решения СЛУ:
- метод Гаусса;
- метод обращения матрицы;
- итерационные методы.
2.4. Метод Гаусса
Пусть имеем систему линейных уравнений:
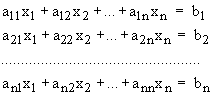
Простой метод Гаусса состоит в следующем.
Составим расширенную матрицу, приписав к матрице коэффициентов СЛУ дополнительный столбец – правые части уравнения:
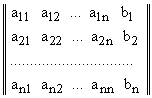 .
.
Выполним над строками расширенной матрицы преобразования, аналогичные тем, которые были описаны в п. 2.1:
![]() ,
,
![]() ,
,
и приведем ее к треугольному виду:
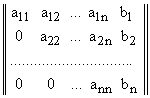 .
.
Теперь можно вычислить искомые величины xi , начиная с последнего, т.е. вначале находится xn , затем xn-1, xn-2, … , x1. Формула для вычислений имеет вид:
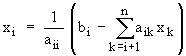 .
.
Для расширения возможностей и повышения устойчивости приведенного алгоритма используется выбор главного элемента. Порядок метода Гаусса равен O(n3).
Похожие работы
... отводилось изучению опыта работы зарубежных библиотек в условиях 2- й мировой войны. Приближался день Великой Победы, библиотеки вписали главную страницу в свою историю, с честью выполнили свой гражданский долг. Библиотечная наука 20 века (1945-1998 гг.) После победоносного окончания Великой Отечественной войны советский народ приступил к мирному созидательному труду. Одной из важнейших ...
... выданных книг, фиксацию возврата книг, просмотра и распечатки отчета задолжников, списание формуляров в архив. 3.5 Расчет вычислительных ресурсов, необходимых для функционирования автоматизированной информационной библиотечной системы АРМ администратора, каталогизатора и библиотекаря объединены (разделение нецелесообразно, так как новые поступления литературы и периодики невелики). Для ...
... , содержащей в себе ведения книжного фонда, регистрация каталога и выдача книг, а также регистрация читателей. Для разработки автоматизированной системы была проектирована инфологическая модель БД библиотечного фонда "Национальной библиотеки им. В.И. Вернадского" и проведен анализ связей между основными объектами данной инфологической модели. Для реализации автоматизированной системы осуществлен ...
... библиотеки. В 1866 году Виленский учебный округ поднял вопрос об открытии русских публичных библиотек, но не получил необходимых для их создания средств. Положительные изменения в развитии библиотечного дела в Беларуси наметились в 70-е гг. XIX века в связи с подъемом борьбы народников. Под влиянием общественности власти вынуждены были пойти на предоставление народу некоторых демократических ...

0 комментариев