Навигация
2.5. Метод обращения матрицы
Представим систему линейных уравнений в матричной форме:
![]() .
.
Умножим последнее равенство слева на A-1 :
![]() .
.
Учитывая, что A-1× A = I , формально получаем искомое решение:
![]()
Таким образом, решение системы выполняется в два этапа:
1) вычисление обратной матрицы;
2) умножение обратной матрицы на вектор правых частей СЛУ.
Несмотря на то, что метод обращения матрицы имеет такой же порядок, как и метод Гаусса - O(n3), по объему вычислений он проигрывает ему в несколько раз. Однако, если СЛУ необходимо решать многократно и при этом изменяется лишь вектор правых частей, метод обращения матрицы становится все же выгодным.
Практическая часть
Описание класса Matrix для решения задач линейной алгебры
Класс имеет приватные и общедоступные члены-данные и члены-функции (методы). Для хранения компонентов матрицы используется одномерный динамический массив элементов типа параметра шаблона. Для создания объекта предусмотрены три конструктора: конструктор по умолчанию, конструктор с параметрами, конструктор копирования и деструктор. Для выполнения множества матричных операций созданы перегруженные операции: присваивания (=), сложения (+), вычитания (-), умножения(*) и т.п. На базе операторов ввода/вывода С++ разработаны функции ввода матриц из потока и вывода их в поток, предусматривающие в случае файлового ввода/вывода как текстовую форму хранения, так и бинарную.
Доступ к членам-данным класса – числу строк и столбцов матрицы осуществляется с помощью методов size_row( ) и size_col( ). Для доступа к элементам матрицы создан перегруженный оператор вызова функции operator( ) (dim x, dim x), где dim – переопределенный тип unsigned char. Вызов функции используется как оператор индексирования, принимающий два аргумента. Аналогично создан оператор вызова функции с одним аргументом operator( ) (dim x). Для данного класса – это очень важные перегруженные операторы, т.к. они используются во всех функциях и операторах, в которых происходит обращение к элементам матрицы.
Описание функций, конструкторов и деструкторов класса:
Конструктор по умолчанию Matrix( ):
Конструктор по умолчанию создает матрицу нулевого размера. В дальнейшем размер этой матрицы можно изменить с помощью функции newsize(i, j).
Конструктор с параметрами Matrix(dim, dim=1):
Это обычный конструктор с параметрами, который принимает в качестве параметров размеры матрицы и создает одномерный динамический массив размером m*n, где m – число строк, а n – число столбцов матрицы. С целью возможности использовать его для создания векторов, второй параметр конструктора задан как умалчиваемый со значением 1. Для первоначальной “инициализации” элементов матрицы нулями используется функция setmem( ).
Конструктор копирования Matrix(const Matrix &):
Конструктор принимает в качестве параметра ссылку на объект класса (на существующую матрицу), определяет ее размер, выделяет для нее память и копирует в эту память содержимое матрицы, принимаемой по ссылке. Таким образом, создается точная копия матрицы с текущими значениями ее элементов.
Деструктор ~Matrix( ):
Деструктор высвобождает память, выделенную конструкторами для элементов матрицы.
Функция операции присваивания "=" Matrix& operator= (Matrix&):
Данная функция сравнивает адрес передаваемого по ссылке объекта с адресом собственного класса, чтобы не предпринялась попытка присвоит объект самому себе. После этого создается новый массив с числом элементов, равным числу элементов массива принимаемого по ссылке, и в этот массив заносится содержимое принимаемого массива. Возвращается разыменованный указатель this (return *this;).
Функции операций суммирования, вычитания, умножения матриц и умножения матрицы на число:
Эти функции реализованы как дружественные функции и алгоритмы этих функций аналогичны по своему составу. Общий вид прототипа этих функций: friend Matrix operator @(const Matrix&, const Matrix&). Применение дружественных функций в данном случае целесообразно для того, чтобы иметь возможность передавать в оператор функцию объекты в любой последовательности. В этих операторах-функциях вначале создается временный объект типа матрица (с помощью конструктора копирования), в который копируется первая матрица и который при выходе из функции является возвращаемым объектом. Затем эта матрица суммируется (вычитается, умножается) с матрицей, стоящей после знака оператора по соответствующим правилам матричных операций. При этом для доступа к элементам матрицы и индексирования используются перегруженные операторы вызова функции operator( ) (dim x, dim x) и operator( ) (dim x).
Функция – оператор Matrix operator^ (int):
Этот оператор-функция реализован как член класса и предназначен для возведения матрицы в степень. В случае, когда значение входного параметра равно минус единице осуществляется вызов функции вычисления обратной матрицы методом преобразований Гаусса, для чего разработана отдельная функция Matrix & Gauss(dim, dim). Таким образом, использование этого оператора позволяет решать систему линейных алгебраических уравнений в представлении X = (A^-1)*B, где X и B –вектора неизвестных и правых частей соответственно.
Функция – оператор Matrix operator ! ( ):
Оператор для определения транспонированной матрицы.
Функция – оператор friend VARTYPE operator %(const Matrix&, const Matrix&):
Функция вычисления скалярного произведения векторов. В ней в начале проверяется, являются ли передаваемые объекты векторами, а затем вычисляется скалярное произведение.
Функции-члены VARTYPE determ( ) и VARTYPE vmodule( ):
Первая функция вычисляет определитель собственного объекта (матрицы). При этом используются функция Matrix & Gauss(dim, dim). Функция VARTYPE vmodule( ) вычисляет длину (модуль) вектора
Функция операции вывода friend ostream& operator<<(ostream&, Matrix&):
Данная функция не может быть членом класса, поэтому чтобы иметь доступ к приватным элементам класса, она объявлена "дружественной" функцией. Она имеет два параметра: ссылку на поток, который находится слева от знака операции <<, и ссылку на объект, который находится слева от знака операции, данные этого объекта и будут выводиться. Затем следует форматированный вывод в поток всех элементов массива и возвращается поток. Если требуется вывести данные в файл, нужно открыть его присоединением к потоку ofstream.
Функция операции ввода friend istream& operator>>(istream&, Matrix&):
Так же как и предыдущая, данная функция не может быть членом класса, а поэтому для доступа к приватным элементам класса объявлена "дружественной" функцией класса. Она так же имеет два параметра: ссылку на поток, который находится слева от знака >>, и ссылку объект, который находится слева от знака операции, в него и будут вводиться данные из потока. Затем следует ввод данных из потока в элементы массива и возвращается поток. Для ввода данных из файла, нужно открыть его присоединением к потоку ifstream.
Функции-члены dim write(ofstream&) и dim read(ifstream&):
Функции предназначены для вывода в файл и ввода из файла матриц в из двоичном представлении. Для этого необходимо передать в них соответствующую ссылку на открытый файл.
Функция void ERROR_MATRIX(dim):
Это функция-член, которая вызывается для фиксации некоторых ошибок при создании матриц и работе с ними, таких как отсутствие памяти, несогласованность размеров матриц при операции умножения, попытки вычислить отрицательную степень матрицы и т.п.
Листинг модуля с определением и реализацией класса матриц
// файл tmatr.cpp
#include <stdlib.h>
#include <mem.h> // для setmem()
#include <fstream.h>
#include <math.h>
typedef unsigned char dim;
template <class VARTYPE> class Matrix {
typedef Matrix Vector;
private:
VARTYPE *matr; // указатель на массив матрицы
dim m,n;// размеры матрицы
public:
// конструкторы и деструкторы:
Matrix() { matr=(VARTYPE*)0; m=n=0; }
Matrix(dim,dim=1); // Обычный конструктор
Matrix(const Matrix<VARTYPE>&); // Конструктор копирования
~Matrix() { delete [ ]matr; }
// доступ к элементам матрицы
dim size_row() { return m; }// число строк
dim size_col() { return n; }// число столбцов
VARTYPE& operator() (dim x) const { return (*this)(x,0); }// элементу
// перегруженные операции и функции:
Matrix<VARTYPE>& operator=(const Matrix<VARTYPE>&);
Matrix<VARTYPE>& operator=(const VARTYPE&);
Matrix<VARTYPE> operator^(int); // возведение в степень
Matrix<VARTYPE> operator!(); // транспонирование
VARTYPE determ(); // определитель матрицы
VARTYPE vmodul(); // модуль вектора
Matrix& Gauss(dim,dim); // преобразование по Гауссу
// (для получ. обратной и единичной матрицы)
// (для получ. верхнетреугольной матрицы)
Matrix minor(dim,dim); // возвращает указ. минор матрицы
Vector line(dim i) // возвращает вектор-строку матрицы
{ return extract(1,n,i,0); }
Vector column(dim j) // возвращает вектор-столбец матрицы
{ return extract(m,1,0,j); }
VARTYPE& operator() (dim,dim) const;// доступ к
Matrix<VARTYPE>& operator<<=(const Matrix &A) { return newsize(A.m,A.n)=A; }
// безусловное приравнивание матриц
Matrix<VARTYPE>& insert(const Matrix&, dim=0, dim=0);// вставить часть матрицы
Matrix<VARTYPE> extract(dim, dim, dim=0, dim=0);// извлечь часть матрицы
Matrix<VARTYPE>& newsize(dim, dim=1);// установить новые размеры
void swap_line(dim, dim);//обмен строками матрицы
void swap_column(dim, dim);// обмен столбцами матрицы
friend Matrix<VARTYPE> operator+(const Matrix<VARTYPE>&,const Matrix<VARTYPE>&);//A-B
friend Matrix<VARTYPE> operator-(const Matrix<VARTYPE>&,const Matrix<VARTYPE>&);//A-B
friend Matrix<VARTYPE> operator*(const Matrix<VARTYPE>&,const Matrix<VARTYPE>&);//A*B
friend Matrix operator*(const double&,const Matrix<VARTYPE>&); //k*A
friend Matrix operator*(const Matrix<VARTYPE>&, const double&); //A*k
friend ostream& operator<<(ostream&,Matrix<VARTYPE>&);
// потоковый вывод матрицы
friend int operator>>(istream&,Matrix<VARTYPE>&);
// потоковый ввод существ. матрицы
// 0 - без. ошибок, 1 - была ошибка
dim read(ifstream&); // файловое чтение и запись матрицы
dim write(ofstream&);// в ее внутреннем, двоичном представлении.
friend VARTYPE operator %(const Matrix<VARTYPE>&,const Matrix<VARTYPE>&);
//Функция ошибок
void ERROR_MATRIX(dim) const;
};
// Реализация класса матриц
template <class VARTYPE>
Matrix<VARTYPE>::Matrix(dim M, dim N)
{
m=M;
n=N;
matr=new VARTYPE[m*n];
if(!matr) ERROR_MATRIX(1);
setmem(matr,sizeof(VARTYPE)*m*n,0);
}
template <class VARTYPE>
Matrix<VARTYPE>::Matrix(const Matrix<VARTYPE> &M_Obj) //Конструктор копирования
{
m=M_Obj.m;
n=M_Obj.n;
matr=new VARTYPE[m*n];
if(!matr) ERROR_MATRIX(1);
movmem(M_Obj.matr, matr, sizeof(VARTYPE)*m*n);
}
template <class VARTYPE>
Matrix<VARTYPE>& Matrix<VARTYPE>::operator=(const Matrix<VARTYPE> &M_Obj)
{
m=M_Obj.m;
n=M_Obj.n;
matr=new VARTYPE[m*n];
if(!matr) ERROR_MATRIX(1);
movmem(M_Obj.matr,matr,sizeof(VARTYPE)*m*n);
return *this;
}
//Диагональ?
template <class VARTYPE>
Matrix<VARTYPE>& Matrix<VARTYPE>::operator=(const VARTYPE &f)
{
for(int i=0,j;i<m;i++) for(j=0;j<n;j++)
if(i==j) (*this)(i,j)=f;
else (*this)(i,j)=0;
return *this;
}
template <class VARTYPE>
Matrix<VARTYPE> Matrix<VARTYPE>::operator^(int q) // Степень
{
if (q>0)
{
for(Matrix M=*this; q>1; q--)
M=M*(*this);
return M;
}
if (q!=-1) ERROR_MATRIX(3);
// вычисление обратной метoдом преобразований Гаусса
if (n!=m) ERROR_MATRIX(4);
Matrix M(m,2*n);
M.insert(*this);
for(int i=0;i<M.m;i++)
M(i,i+M.m)=1;
for(i=0;i<M.m;i++)
M.Gauss(i,i);
return M.extract(M.m,M.m,0,M.m);
}
template <class VARTYPE>
Matrix<VARTYPE> Matrix<VARTYPE>::operator!() // Транспозиция
{ Matrix<VARTYPE> A(n,m);
for(int i=0, j; i<m; i++)
for(j=0; j<n; j++)
A(j,i)=(*this)(i,j);
return A;
}
template <class VARTYPE>
VARTYPE Matrix<VARTYPE>::determ() // рекурсивно находит определитель матрицы
{
if (n!=m) ERROR_MATRIX(4);
if (n==1)
return (*this)(0,0);
for(int i=0; i<m; i++)
if ((*this)(i,0))
{
static Matrix<VARTYPE> M;
M <<= *this;
VARTYPE d=M(i,0)*(i%2?-1:1);
return d*M.Gauss(i,0).minor(i,0).determ();
}
return 0.0;
}
template <class VARTYPE>
VARTYPE Matrix<VARTYPE>::vmodul() // Модуль вектора
{
VARTYPE d=0;
if (n!=1) ERROR_MATRIX(9);
static Matrix<VARTYPE> M;
M <<= *this;
for(int i=0; i<m; i++)
d=d+M(i,0)*M(i,0);
return sqrt(d);
}
template <class VARTYPE>
Matrix<VARTYPE>& Matrix<VARTYPE>::Gauss(dim M, dim N)
{
Matrix<VARTYPE>& A=*this;
if (!A(M,N)) ERROR_MATRIX(5);
for(int i=0,j;i<m;i++)
for(j=0;j<n;j++)
if (i!=M && j!=N)
A(i,j)-=A(M,j)*A(i,N)/A(M,N);
for(j=0;j<n;j++)
if (j!=N)
A(M,j)/=A(M,N);
for(i=0;i<m;i++)
A(i,N)=0;
A(M,N)=1;
return *this;
}
template <class VARTYPE>
Matrix<VARTYPE> Matrix<VARTYPE>::minor(dim M, dim N)// возвращ. матрицу без
{// строки y и столбца x
Matrix<VARTYPE> A(m-1,n-1);
for(int i=0,in=0,j,jn;i<m;i++)
if (i!=M)
{
for(j=0,jn=0;j<n;j++)
if (j!=N)
A(in,jn++)=(*this)(i,j);
in++;
}
return A;
}
template <class VARTYPE> // вставка
Matrix<VARTYPE>& Matrix<VARTYPE>::insert(const Matrix<VARTYPE> &A, dim M, dim N)
{
if (M+A.m>m || N+A.n>n) ERROR_MATRIX(6);
for(int i=0, j; i<A.m; i++)
for(j=0; j<A.n; j++)
(*this)(i+M,j+N)=A(i,j);
return *this;
}
template <class VARTYPE> // извлечение
Matrix<VARTYPE> Matrix<VARTYPE>::extract(dim LM, dim LN, dim M, dim N)
{
if (M+LM>m || N+LN>n) ERROR_MATRIX(7);
Matrix<VARTYPE> A(LM,LN);
for(int i=0, j; i<LM; i++)
for(j=0; j<LN; j++)
A(i,j)=(*this)(i+M,j+N);
return A;
}
template <class VARTYPE>
VARTYPE& Matrix<VARTYPE>::operator() (dim M, dim N) const
{ return *(matr+n*M+N); }
template <class VARTYPE>
Matrix<VARTYPE> operator+(const Matrix<VARTYPE> &A, const Matrix<VARTYPE>&B)
{
Matrix<VARTYPE> C=A;
for(int i=0,j; i<A.m; i++)
for(j=0; j<A.n; j++)
C(i,j)+=B(i,j);
return C;
}
template <class VARTYPE>
Matrix<VARTYPE> operator-(const Matrix<VARTYPE> &A, const Matrix<VARTYPE> &B)
{
Matrix<VARTYPE> C=A;
for(int i=0, j; i<A.m; i++)
for(j=0;j<A.n;j++)
C(i,j)-=B(i,j);
return C;
}
template <class VARTYPE>
Matrix<VARTYPE> operator*(const Matrix<VARTYPE> &A,const Matrix<VARTYPE> &B)
{
Matrix<VARTYPE> C(A.m,B.n);
if (A.n!=B.m)
{
if(A.m==3 && A.n==1 && B.m==3 && B.n==1)
{
C(0)=A(1)*B(2)-A(2)*B(1);
C(1)=A(2)*B(0)-A(0)*B(2);
C(2)=A(0)*B(1)-A(1)*B(0);
}
else
A.ERROR_MATRIX(2);
}
else
{
for(int i=0,j,k;i<C.m;i++)
for(j=0;j<C.n;j++)
for(k=0;k<A.n;k++)
C(i,j)+=A(i,k)*B(k,j);
}
return C;
}
template <class VARTYPE>//умножение числа на матрицу
Matrix<VARTYPE> operator*(const double &f,const Matrix<VARTYPE> &A)
{
Matrix<VARTYPE> B=A;
for(int i=0,j;i<A.m;i++)
for(j=0;j<A.n;j++)
B(i,j)*=f;
return B;
}
template <class VARTYPE>// умножение матрицы на число
Matrix<VARTYPE> operator*(const Matrix<VARTYPE> &A, const double &f)
{
Matrix<VARTYPE> B=A;
for(int i=0,j;i<A.m;i++)
for(j=0;j<A.n;j++)
B(i,j)*=f;
return B;
}
template <class VARTYPE>
Matrix<VARTYPE>& Matrix<VARTYPE>::newsize(dim M, dim N)
{ delete [] matr;
m=M;
n=N;
if (N && M) { matr=new VARTYPE[m*n];
if (!matr) ERROR_MATRIX(1);
setmem(matr,sizeof(VARTYPE)*m*n,0); }
else { m=n=0; matr=(VARTYPE*)0; }
return *this;
}
template <class VARTYPE>
ostream& operator<<(ostream &out,Matrix<VARTYPE> &A)
{ for(int i=0,j;i<A.size_row();i++)
{ for(j=0;j<A.size_col();j++)
out << A(i,j)<< " ";
out<<endl;
}
return out;
}
template <class VARTYPE>
int operator>>(istream &inp,Matrix<VARTYPE> &A)
{ for(int i=0,j;i<A.size_row();i++)
for(j=0;j<A.size_col();j++) if( !(inp>>A(i,j)) ) return 1;
return 0;
}
template <class VARTYPE>
void Matrix<VARTYPE>::swap_line(dim L1, dim L2)
{
if (L1==L2)
return;
double b;
for(int j=0;j<n;j++)
{
b=(*this)(L1,j);
(*this)(L1,j)=(*this)(L2,j);
(*this)(L2,j)=b;
}
}
template <class VARTYPE>
void Matrix<VARTYPE>::swap_column(dim C1, dim C2)
{
if (C1==C2)
return;
double b;
for(int i=0;i<m;i++)
{
b=(*this)(i,C1);
(*this)(i,C1)=(*this)(i,C2);
(*this)(i,C2)=b;
}
}
template <class VARTYPE>
dim Matrix<VARTYPE>::read(ifstream &finp)
{ (finp.get(m)).get(n); delete []matr; matr=new VARTYPE[m*n];
if(!matr) ERROR_MATRIX(1);
setmem(matr,sizeof(VARTYPE)*m*n,0);
finp.read((char *)matr,sizeof(VARTYPE)*m*n); return finp.fail();
}
template <class VARTYPE>
dim Matrix<VARTYPE>::write(ofstream &fout)
{ (fout.put(m)).put(n);
(fout.write((char *)matr,sizeof(VARTYPE)*m*n))<<flush; return fout.fail();
}
template <class VARTYPE>
VARTYPE operator%(const Matrix<VARTYPE> &A, const Matrix<VARTYPE>&B)
{
if(A.n!=1 || B.n!=1) A.ERROR_MATRIX(9);
if(A.m!=B.m) A.ERROR_MATRIX(0);
VARTYPE scalarmul = 0;
for(int i=0; i<A.m; i++)
scalarmul = scalarmul+A(i)*B(i);
return scalarmul;
}
template <class VARTYPE>
void Matrix<VARTYPE>::ERROR_MATRIX(dim E) const
{ static char *message[] = {
"Матрицы должны иметь одинаковую размерность",//0
"Не выделена память!",//1
"Матрицы не согласованы для умножения",//2
"Степень должна быть больше нуля или -1",//3
"Матрица должна быть квадратной",//4
"Нулевой ведущий элемент в преобразовании Гаусса",//5
"Вставка невозможна из-за перекрытия базовой матрицы",//6
"Извлекаемая матрица выходит за границы базовой",//7
"Выход за границы. Попытка доступа к несущ. элементу",//8
"Это не вектор!"};//9
cerr<<"ERROR: "<< message[E] << endl; exit(1);
}
Демонстративно - тестирующая программа:
#include <conio.h>
#include <iostream.h>
#include <fstream.h>
#include "tmatr.cpp"
int main()
{
clrscr();
Matrix<double> A(3,3), B(3,3), C(3,3);
Matrix<double> V(3),X(3),H(3),U(3);
double d;
A(0,0)=1.1; A(0,1)=2.2; A(0,2)=3.3;
A(1,0)=2.4; A(1,1)=1.1; A(1,2)=4.4;
A(2,0)=1.3; A(2,1)=2.1; A(2,2)=4.1;
B(0,0)=2; B(0,1)=7; B(0,2)=2;
B(1,0)=4; B(1,1)=8; B(1,2)=1;
B(2,0)=6; B(2,1)=4; B(2,2)=1;
V(0)=2.1; V(1)=3.31; V(2)=1.4;
H(0)=1.1; H(1)=2.1; H(2)=3.1;
//******************************
C=A+B;
cout<<"A:n"<<A<<endl;
cout<<"B:n"<<B<<endl;
cout<<"C=A+B:n"<<C<<endl;
cout<<"Press any key...n";
getch();
clrscr();
//******************************
C=A-B;
cout<<"A:n"<<A<<endl;
cout<<"B:n"<<B<<endl;
cout<<"C=A-B:n"<<C<<endl;
cout<<"Press any key...n";
getch();
clrscr();
//******************************
//******************************
X=V+H;
cout<<"V:n"<<V<<endl;
cout<<"H:n"<<H<<endl;
cout<<"X=V+H:n"<<X<<endl;
cout<<"Press any key...n";
getch();
clrscr();
//******************************
X=V-H;
cout<<"V:n"<<V<<endl;
cout<<"H:n"<<H<<endl;
cout<<"X=V-H:n"<<X<<endl;
cout<<"Press any key...n";
getch();
clrscr();
C=A*V;
cout<<"A:n"<<A<<endl;
cout<<"V:n"<<V<<endl;
cout<<"C=A*V:n"<<C<<endl;
cout<<"Press any key...n";
getch();
clrscr();
//******************************
Matrix<int> D(3,3), E(3,3);
D(0,0)=1; D(0,1)=2; D(0,2)=3;
D(1,0)=2; D(1,1)=5; D(1,2)=6;
D(2,0)=7; D(2,1)=3; D(2,2)=9;
ofstream fout("test.mtr");
if(!fout)
{
cout<<"file not openn";
return 1;
}
D.write(fout);
fout.close();
ifstream fin("test.mtr");
if(!fin)
{
cout<<"file not openn";
return 1;
}
E.read(fin); //
cout<<"D:n";
cout<<D;
cout<<"E:n";
cout<<E;
fin.close();
cout<<"Press any key...n";
getch();
clrscr();
//************************************
C=A^-1;
cout<<"A:n"<<A<<endl;
cout<<"C=A^-1:n"<<C<<endl;
cout<<"Press any key...n";
getch();
clrscr();
//****************************
// A*X=V X=(A^-1)*V
X=(A^-1)*V;
cout<<"A^-1:n"<<(A^-1)<<endl;
cout<<"V:n"<<V<<endl;
cout<<"X:n"<<X<<endl;
cout<<"Press any key...n";
getch();
clrscr();
//************************************
d=A.determ();
cout<<"determinant of A = "<<d<< endl;
d=V.vmodul();
cout<<"modul of V = "<<d<< endl;
cout<<"Press any key...n";
getch();
clrscr();
//************************************
V(0)=4; V(1)=3; V(2)=2;
U(0)=1; U(1)=2; U(2)=3;
d=V%U;
cout<<"scalar product V*U= "<< d<<endl;
cout<<"Press any key...n";
getch();
clrscr();
//************************************
C=!A;
cout<<"A:n"<<A<<endl;
cout<<"C=!A:n"<<C<<endl;
cout<<"Press any key...n";
getch();
clrscr();
C=5*A;
B=A*2;
cout<<"A:n"<<A<<endl;
cout<<"C=5*A:n"<<C<<endl;
cout<<"B=A*2:n"<<B<<endl;
cout<<"Press any key...n";
getch();
clrscr();
//************************************
//************************************
return 0;
Результаты тестирования класса Matrix
Сложение матриц A и B:
A:B:C=A+B:
1.12.23.32723.19.25.3
2.41.14.44816.49.15.4
1.32.14.16417.36.15.1
Вычитание матриц A и B:
A:B:C=A-B:
1.12.23.3272-0.9-4.81.3
2.41.14.4481-1.6-6.93.4
1.32.14.1641-4.7-1.93.1
Сложение матриц A и B:
A:B:C=A*B:
1.12.23.327230.838.57.7
2.41.14.448135.643.210.3
1.32.14.164135.642.38.8
Сложение векторов
V:
2.1
3.31
1.4
H:
1.1
2.1
3.1
X=V+H
3.2
5.41
4.5
Вычитание векторов
V:
2.1
3.31
1.4
H:
1.1
2.1
3.1
X=V-H:
1
1.21
-1.7
Умножение матрицы на вектор
A:
1.1 2.2 3.3
2.4 1.1 4.4
1.3 2.1 4.1
V:
2.1
3.31
1.4
C=A*V:
14.212
14.841
15.421
Запись матрицы в файл
D:
1 2 3
2 5 6
7 3 9
Считывание матрицы из файла
E:
1 2 3
2 5 6
7 3 9
Вычисление обратной матрицы
A:
1.1 2.2 3.3
2.4 1.1 4.4
1.3 2.1 4.1
C=A^-1:
2.009346 0.88785 -2.570093
1.750212 -0.093458 -1.308411
-1.53356 -0.233645 1.728972
Решение алгебраического уравнения
A^-1:
2.009346 0.88785 -2.570093
1.750212 -0.093458 -1.308411
-1.53356 -0.233645 1.728972
V:
2.1
3.31
1.4
X:
3.56028
1.534325
-1.57328
Определение детерминанта матрицы
determinant of A = -2.354
Определение длины (модуля) вектора
modul of V = 4.162463
Вычисление скалярного произведения векторов
scalar product V*U= 16
ВЫВОД
В результате выполнения курсового проекта были разработаны два класса функций для решения простейших задач линейной алгебры. Число этих функций сравнительно невелико, однако можно легко добавить в эти классы более сложные функции, построенные на базе уже имеющихся. Классы позволяют работать с матрицами и векторами, элементы которых могут быть любого типа, однако на практике чаще всего используется целый тип и тип чисел с плавающей запятой.
Классы написаны на языке С++, однако могут быть легко переписаны на любом из современных языков программирования, так как приведены довольно простые алгоритмы всех компонентных функций. Были максимально предусмотрены все возможные ошибки, которые могут возникнуть при использовании функций данных классов. Особое внимание уделялось разумному выделению памяти под объекты во время выполнения программы, поэтому все функции были тщательно отлажены.
Классы Matrix и Vector могут быть эффективно применены на практике в задачах, требующих операций с матрицами и векторами, а также связанных с решением систем линейных алгебраических уравнений.
Список использованной литературы
Дискретная математика, конспект лекций. В. Г. Засовенко. Запорожье, 1998 г.
Начальный курс С и С++. Б. И. Березин. Москва: "ДИАЛОГ-МИФИ", 1999 г.
Язык программирования С++. Б. Страуструп. Киев:"ДиаСофт", 1993
Похожие работы
... отводилось изучению опыта работы зарубежных библиотек в условиях 2- й мировой войны. Приближался день Великой Победы, библиотеки вписали главную страницу в свою историю, с честью выполнили свой гражданский долг. Библиотечная наука 20 века (1945-1998 гг.) После победоносного окончания Великой Отечественной войны советский народ приступил к мирному созидательному труду. Одной из важнейших ...
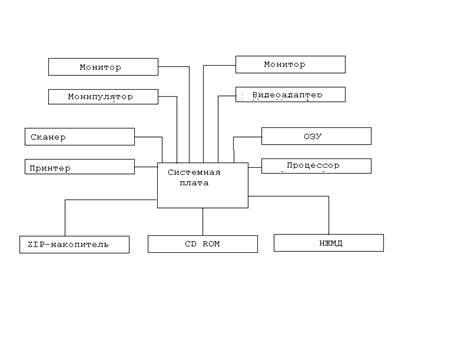
... выданных книг, фиксацию возврата книг, просмотра и распечатки отчета задолжников, списание формуляров в архив. 3.5 Расчет вычислительных ресурсов, необходимых для функционирования автоматизированной информационной библиотечной системы АРМ администратора, каталогизатора и библиотекаря объединены (разделение нецелесообразно, так как новые поступления литературы и периодики невелики). Для ...
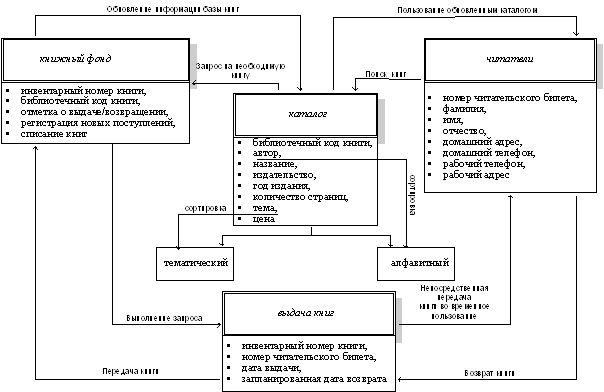
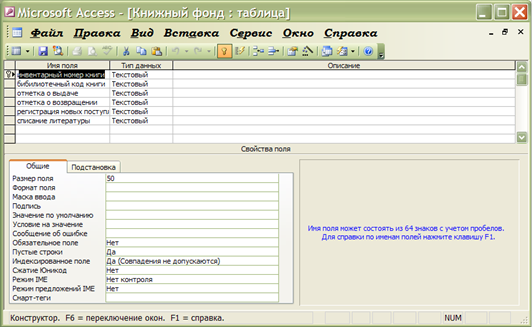
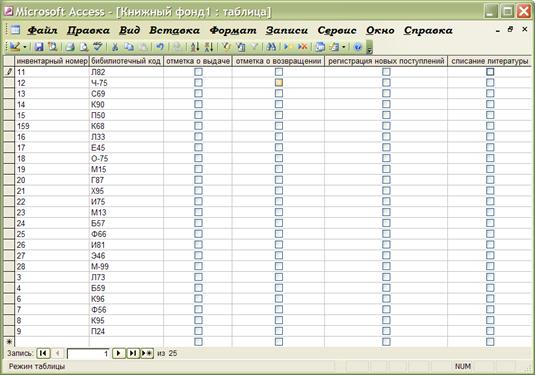
... , содержащей в себе ведения книжного фонда, регистрация каталога и выдача книг, а также регистрация читателей. Для разработки автоматизированной системы была проектирована инфологическая модель БД библиотечного фонда "Национальной библиотеки им. В.И. Вернадского" и проведен анализ связей между основными объектами данной инфологической модели. Для реализации автоматизированной системы осуществлен ...
... библиотеки. В 1866 году Виленский учебный округ поднял вопрос об открытии русских публичных библиотек, но не получил необходимых для их создания средств. Положительные изменения в развитии библиотечного дела в Беларуси наметились в 70-е гг. XIX века в связи с подъемом борьбы народников. Под влиянием общественности власти вынуждены были пойти на предоставление народу некоторых демократических ...

0 комментариев