Расчет преднапряженых стенок

3. Расчет преднапряженых стенок.

Задаемся типом проволоки, ее диаметром «d», шагом навивки «а».Определяем площадь сечения проволоки

f= (см2);

Приведенная толщина обмотки

tпр= (см),

а – шаг навивки.

Критическое напряжение стенки, при потере ее устойчивости, вызванное преднапряжением равно:

scr=0,58( *tci*tпр)^1/2

Е=21000 кн/см2; R=1995 см – радиус резервуара; m=0,3 – коэффициент Пуассона;

м=Епр/Е; Е – модуль упругости проволоки.

Толщину tci каждого пояса предварительно определяем исходя из расчета однослойной стенки так, чтобы она была меньше 17 мм, что обеспечивает возможность рулонирования.

Задаемся величиной преднапряжения в стенке

s01=(0,7 – 0,8)scr

Величина преднапряжения в проволоке будет равна

sпр= (кн/см2)

Определяем толщины i – того пояса стенки «tci» и приведенную толщину проволоки «tпр»

tci= (см);

tnp= (см);

K= ;

Rnp-расчетное сопротивление проволоки.

Диаметр проволоки равен:

D= ( )^1/2 (см)

Если tci сильно (более, чем на 20%) отличается от принятого предварительно, меняем параметры a, tci, d, Rnр и повторен расчет до сходимости (с разницей <=20%).

Окончательно производим проверку напряжений:

sст= - s01<=gcRy ;

snp= + sпр <=gс' Rпр ;

m=0,3.

Так как стенку можно рулонировать, то оставляем данные параметры, но проволока будет сильно недонапряжена.

С целью экономии материала примем вместо высокопрочной проволоки В-2 проволоку В-1 и повторим расчет.

Rпр=34 кн/см2 ;

Епр=1,7*104 кн/см2; тогда

к= =1,478;

= =0,8095;

Так как проволока В-1 работает эффективнее проволоки В-2, то оставляем данные параметры.

Расчет узла сопряжения стенки и днища

(«краевой эффект» ).

Расчетная схема нижнего узла сопряжения и основная система метода сил указаны на рисунке №

Канонические уравнения метода сил для определения изгибающего момента «М0» и поперечной силы в оболочке Q0имеют вид:

(d11с+d11д)М0+d12сQ0+ Δ1pс+Δ1pд+Δ1pд(N1)=0;

d21c М0+d22сQ0+ Δ2pс =0.

В качестве исходных данных возьмем данные из второго варианта расчета стенки.

tci=1,7 мм; Е=21000 кн/см2 ; R=1995 см; Ry=31,5 кн/см2.

Примем песчаное основание, с коэффициентом постели kg=0,05 кн/см3 ;

Толщина окрайка днища t0=1,4 см. Тогда :

kc= = =0,00896 кн/см3;

Цилиндрическая жесткость стенки определяется по формуле:

Dc= =21000*1,7^3/(12-(1-0,3^2))= 9448,08 (кн см);

Цилиндрическая жесткость днища определяется по формуле:

Dд= =21000*1,4^3/(12*(1-0,3^2)) = 5276,92 (кн см) ; где

Е=21000 кн/см2 – модуль Юнга;

m=0,3 – коэффициент Пуассона.

Формулы для определения перемещений:

Стенка.

d11с= =1/(9448*0,02206) = 0,0048;

d12c=d21c= - =-1/(2*9448*0,02206^2) = -0,10875;

d22c= =1/(2*9448*0,02206^3) = 4,92962;

mc= ( )1/4 =(0,00896/(4*9448))^(1/4) = 0,0220662 (1/см);

Знаки взяты для усилий, указанных на рисунке

Днище.

d11д= [В.В.1] =(1+0,965^2+2*0,8024^2)/(4*5276,9*0,0392) = 0,00389032;

x0=mд с = 0,0392*5 =0,196;

с=4 – 10 см – величина выступа окрайка за стенку; принимаем с=5 см;

mд=( )1/4 =(0,05/(4*5276,92))^(1/4) =0,039231;

Значения функций j(x0)=e-xo[cos(x0)+sin(x0)]; q(x0)=e-xocos(x0) принимаем по приложению № 4.

Грузовые члены Δip взяты со знаками, соответствующими направлению усилий и нагрузок на рис.

Стенка.

Δ1pс= =0,01544/(0,00896*1788) = 0,0009637664;

Δ2pс= - Δ1pс Нс =-0,000963*1788 = -1,721844;

 Нс =1788 см полная высота стенки резервуара.

Ру0=gf1 r Hж+gf2 Pи =1*0,0000085*1788+1,2*0,0002 = 0,015438 (кн/см2) – полное расчетное давление на стенку gf1=1, gf2=1,2.

Объемная масса «r» и избыточное давление «Ри» определены ранее при расчете стенки; Нж- высота столба жидкости в см, обычно Нж=Нс.

Днище.

Δ1pд= [1-j(x0) y(x0)+2 q(x0) x(x0)] = 0,003872;

Значения функций : x(x0)=e-xo sin(x0); y(x0)=e-xo[cos(x0)-sin(x0)];

q(x0)=e-xocos(x0);

принимаем по приложению № 4.

Δ1p(N1)= q2(x0) =0,2758/(2*0,0392*5276,92)*0,8024= 0,00053492

N1x=N1k+N1c+N1p =0,0612+0,0245+0,19015 =0,27585 кн/см;

N1к=0,0612 кн/см;

N1c=0,0245 кн/см;

N1p=0,19015 кн/см;

Решив систему уравнений получим:

М0=4,59 кн см =459 кг см;

Q0=0,45 кн.

Проверка напряжений

Напряжения в зоне нижнего узла резервуара.

Стенка. У=0.

s1 =+- - - m <=gcRy ;

gc=1,2 (в месте сопряжения)

Ry=23 кн/см.

N2=Py R=1995*0,01518 =30,2841 кн/см ;

s1= -(4,59*6/(1,7^2))-2,758/1,7-0,3*30,28/1,7 = -16,4953 < 1,2*31,5 ;

s2= + m <=gcRy ;

s2=30,28/1,7+0,3*6*4,59/(1,7^2)=20,671 < 1,2*31,5 ;

τ ==0,45/1,7=0,265

_______________

sпр=√s12-s1s2+s22+3 τ2 <=gcRy ;

sпр=32,25259 <31,5*1,2=37,8 ;

Проверка выполнена.

Днище.

s1=+- + <=gcRy ;

s2=m s1;

__________

sпр= √ s12-s1s2+s2 <=gсRy ;

gc=1,2.

Вычислим изгибающий момент в днище справа от сечения х0 = mд с (считая от края днища).

Мд=[1+j2(х0)] - x(x0)- [1-2q(x0) x(x0)-y(x0) j(x0)] = 1,473921 (кн см); тогда

s1=4,821 <=1,2*31,5=37,8 ;

s2=0,3*4,821=1,446;

sпр=4,20914

Проверка выполнена.

Расчет сферического купола.

Выполняем сферическую крышу в виде ребристого купола. Анализ различных конструктивных решений показал, что при симметричных нагрузках ребристый купол имеет меньшую массу и стоимость. При несимметричных нагрузках сетчатые и ребристо – кольцевые купола являются более надежными и жесткими конструкциями, чем ребристые, но не имеющими лучшие технико – экономические показатели.

Ребристый купол имеет основные конструктивные элементы: ребра – арки, наружное и внутреннее опорные кольца. Настил опирается на балочки и не является несущим элементом. Наружное кольцо мешает горизонтальным деформациям. Возникают горизонтальные реакции – распор. Стенка резервуара служит неподвижной опорой.

Ребро – арка может опираться на внутреннее кольцо двумя способами: шарнирное опирание и жесткое защемление. Если ребро приварить к внутреннему кольцу, то его можно считать как двухшарнирную арку с затяжкой. Роль затяжки играет внешнее кольцо, работающее на растяжение. Средний шарнир отсутствует.

Если ребра крепятся к внутреннему кольцу болтами, то ребро рассчитывается как трехшарнирная арка с упругой затяжкой.

Радиус кривизны Rк =(1,2 – 1,5)L;

Стрела подъема f0=(1/10 – 1/12)L=340 см;

Зная стрелу подъема, радиус кривизны определяется по формуле:

Rк= + =39,9^2/(8*3,4)+3,4/2 =60,23 м;

Определим количество ребер в куполе:

n = m/2 =42/2 =21; m= = 41,7831816 ≈ 42;

a=300 см;

Определим нагрузки.

q=q1+q2=0,018269+0,0094=0,027696

q1= a =730*1,05/(3,1415*1995^2)*298 = 0,018269 кн/см;

q2= gf2*S0*m*k1*a=0,7*0,5*1*0,315*298=0,0094 кн/см;

1.Статический расчет арки.

Прежде всего определяем площадь условной затяжки:

FЗ= =2*3,1415926*100/42 = 14,9599648≈15 см2;

Fи – площадь сечения опорного кольца.В реальных резервуарах колеблется в пределах от 90 до 120 см2. Предварительно принимаем Fи=100 см2.

m=2n; n – число арок в куполе.

А). Двухшарнирная арка.

V= =0,027696*3990/4 =27,62676 кн.

Распор в арке:

Н=0,0456k=730*1,05/(3,1415*19956^2)*298 =29,094699 кн;

К=0,492.

Определим расчетные усилия в различных сечениях арки:

х=L/2=1995 см; y=f0 =340 см; ά=0; сos ά=1; sin ά=0;

Mб=V*x - =27,62*1995-0,027696*3990^2/12 =18358,3092 кнсм;

Ма=Мб – Н*y=18358,3-29,09*340 =8467,7 кнсм;

N= - (Qб sin ά +H сos ά) = - 29,09*1= - 29,09 кн;

х= L/4=3990/4=998 см; y=f – Rи(1-cos ά)=254 см;

tg ά0= =3990/(2*(6023-340))=0,3520 ; ά0=19,340 ; ά= ά0/2=9,670;

сos ά=0,9858; sin ά=0,168;

Мб= V*x - qx - (q – qx) =27,62*998-0,0138*998^2/2-(0,027696-0,0138)*998^2/3 =16078,841872 кнсм;

qx=q - q = 0,027696-0,027696*2*998/3990 =0,013841 кн/см;

Ма=Мб – Н*y=16078,8-29,09*254 =8689,94 кнсм;

N= - (Qб sin ά - H сos ά) =-(6,91*0,168+29,09*0,9858) =-29,8378 кн;

 Qб=V - x=27,62-998*((0,027696+0,0138)/2) =6,913496 кн.

Проверка напряжений.

 Примем сечение ребра двутавр №27а; Wx=407 см3; А=43,2 см2; Ix=5500 cм4; х=L/4=998 см.

Прочность:

s= - - =-8689,94/407-29,83/43,2 = -22,042 кн/см2 < 1*24=24 кн/см2;

проверка прочности выполнена.

Устойчивость:

1,4*Nx<= Nкр;

Nкр= =3,14^2*21000*5500/(1,06*((4094/2)^2)) = 256,3892 кн;

m=1,06; S1=2 Rи ά0 = 2*6030*0,34=4094 см;

Nx= 1,4*29,83=41,76 кн <Nкр= 256 кн.

Устойчивость обеспечена.

Б). Трехшарнирная арка.

V= =0,027696*3990/4 =27,62676 кн.

Распор:

Н= =18371,895/340 =54,035

М0= =0,027696*(3990^2)/24 =18371,7954 кнсм.

х= L/4=3990/4=998 см; y=f – Rи(1-cos ά)=254 см;

tg ά0= =3990/(2*(6023-340))=0,3520 ; ά0=19,340 ; ά= ά0/2=9,670;

сos ά=0,9858; sin ά=0,168;

Мб= V*x - qx - (q – qx) =27,62*998-0,0138*998^2/2-(0,027696-0,0138)*998^2/3 =16078,841872 кнсм;

qx=q - q = 0,027696-0,027696*2*998/3990 =0,013841 кн/см;

Усилия в сечении х=L/4:

Ма=Мб – Н*y=16078,8-54,035*254 =2353,91 кнсм;

N= - (Qб sin ά - H сos ά) =-(6,91*0,168+54,035*0,9858) =-54,4286 кн;

 Qб=V - x=27,62-998*((0,027696+0,0138)/2) =6,913496 кн.

Проверка напряжений.

Примем сечение ребра двутавр № 20а, Wx=203 см3; А=28,9 см3;Ix=2030 cм4.

Прочность:

s= - - = 2353,91/203+54,428/28,9 =13,4789 < 24*1=24 кн/см2;

Устойчивость:

1,4*Nx<= Nкр;

Nкр= =3,14^2*21000*2030/(1,2*((4094/2)^2)) = 83,5906 кн;

m=1,2; S1=2 Rи ά0 = 2*6030*0,34=4094 см;

Nx= 1,4*54,428=76,199 кн <Nкр= 83,59 кн.

Устойчивость обеспечена.

Принимаем трехшарнирную арку.

Расчет опорного кольца арки.

Нижнее опорное кольцо расчитывается на два сочетания нагрузки:

собственный вес купола с коэффициентом надежности по нагрузке gf1=0,9 и внутреннее избыточное давление газа Ри=0,0002 кн/см2 с коэффициентом gf2=1,2; в этом случае опорное кольцо сжимается;

собственный вес крыши с коэффициентом gf1=1,1 и снеговой нагрузки с коэффициентом gf2=1,4 ; а также вакуум Рвак=0,000025 кн/см2 с коэффициентом gf3= 1,2. При таком сочетании опорное кольцо растягивается.

Первое сочетание:

q=q’+q”=0,01566-0,07152= -0,05586 кн/см;

q’= a=730*0,9/(3,1415*1995^2)*298 =0,01566 кн/см;

q”= - P0 gf2 a =-0,00024*298 =-0,07152 кн/см;

a==298 см;

m=2 n=42;

Втрое сочетание.

q=q1+q2 =730*1,05/(3,1415*1995^2)*298+0,7*0,5*0,8*1/10000*298 =0,026613 кн/см;

Вычислим изгибающие моменты и осевые усилия.

Распор.

Двухшарнирная арка:

Н=0,0456 k (кн);

k=0,492.

Трехшарнирная арка:

 Н=

М0=

Вертикальная реакция.

V= (кн);

Усилие в кольце равно:

Nk= (кн);

От действия сосредоточенных усилий распор «Н» в кольце возникают изгибающие моменты в плоскости кольца:

Мк= [ - ] (кнсм);

Здесь α=2 p/m – угол между ребрами в радианах; β – величина угла в пределах от 0 до α;

М0 – изгибающий момент в сечении, где опираются ребра (β=0; α=2*p/42=0,1495);

Мпр – изгибающий момент в сечении между арками (β= α/2; α/2=0,0748 рад).

Результаты вычислений приведены в таблице № 12.

Таблица № 12.

Расчетная схема		Первое сочетание нагрузок				Второе сочетание нагрузок
		Н	Nк	Mо	Mпр	Н	Nк	Mо	Mпр
2-хшарнирная арка		-58,681	-392,254	-1454,38	733,9951	27,94335	1843,519	692,5619	-349,521
3-хшарнирная арка		-108,982	-728,494	-2701,08	1363,176	51,8964	3423,785	1286,226	-649,132

Проверка прочности и устойчивости нижнего опорного кольца.

Примем следующее сечение кольца:

Геометрические характеристики сечения:

Площадь А=30,6+40*1+80*1+30*25=225,6 см2;

ус= =39,4 см;

Iy=208+30,6(80-2,4-39,4)2 +40*1(80+ - 39,4)2 +30*2,5*39,42 + +80*1( - 39,4)2 =659377 см4;

Wy1= =16240 см3; Wy2= =15388 см3 .

Прочность кольца.

Проверка производится по формуле:

sк= + <=gcRy ; gc=0,9;

Nк – усилие от действия второго сочетания нагрузок;

Mmax – максимальный изгибающий момент из М0 и Мпр;

Wy min – минимальный момент сопротивления из двух Wy1 и Wy2 .

Двухшарнирная арка.

sк=1843,519/225,6 + 692,56/15388=8,22 кн/см2 <23*0,9=20,7 кн/см2;

Проверка выполнена.

Трехшарнирная арка.

sк=3423,78/225,6 + 1286,2/15388 =15,26 кн/см2<20,7 кн/см2.

Проверка выполнена.

Устойчивость кольца.

Расчет ведется по первому сочетанию нагрузок (в случае, если величина Nк отрицательная величина).

sк= - - <=scrgc ; gc=0,9;

scr= (кн/см2) ; Е=2,1*104.

Двухшарнирная арка.

scr=3*21000*659377/19953 = 5,23 кн/см2 ;

sк= - 392,25/225,6 – 1454,38/15388 = 2,68 кн/см2<5,23 кн/см2;

Устойчивость обеспечена.

Трехшарнирная арка.

sк= - 728,49/225,6 – 2701,08/15388 =3,4 кн/см2<5,23 кн/см2;

Устойчивость обеспечена.

Расчет промежуточного кольца жесткости.

Промежуточные кольца жесткости устанавливаются на корпусе для обеспечения устойчивости стенки.

Расчет кольца на суммарное давление ветра и вакуума.

В данном случае кольцо работает на сжатие и его следует проверить на устойчивость по формуле:

Р0 <= ; где

Р0 = Рвак *1,2 + 1,4*w0*0,5*C=0,000025*1,2+1,4*(0,3/10000)*0,5*1 =0,000051 кн/см2;

Рвак=0,000025 кн/см2 ; w0 =0,3 кн/м2 – скоростной напор ветра в районе Днепропетровска.

С=1;

 y0=894 cм – ширина оболочки, с которой передается ветровая нагрузка на кольцо.

Iy – момент инерции сечения ребра отнсительно оси проходящей через центр тяжести сечения.

Iy= Iугол+Fугол*а2+F - *(x – y)2 39,53+7,39*4,79^2 + 30*4,79^2= 897,41 см4;

S11=Fугол*x =7,39*5,98=44,192 см3;

х=75-z0+tст/2 =7,5-2,02+0,5 =5,98 см ;

у= S11/F = 44,192/37,39=1,181 см;

Проверка :

Р0 =0,0000051 кн/см2< = 0,00000796 кн/см2.

Проверка выполнена.

Радиальный момент в стенке в месте промежуточного ребра.

Mк= = 4,66493056 ;

mcт=( )^(1/4) = 0,0288;

Р= =0,537410341 ;

s1 = = 18,64 < 23*1 кн/см2;

Напряжение s2 (в кольце и стенке)

s2= =9,4220785 кн/см2 < 23*1 кн/см2;

S=0,6(R*tст)^(1/2) = 26,8 ;

Проверка выполнена.

Сравнение вариантов.

Стенка.

Для выбора варианта сравним массы стенок.

№ п/п	Тип стенки	Толщины поясов	Масса стенки, т	Относительная масса,%
1	Однослойная из стали С 255	25+18+17+16+14+12+11+5*10	238,98	100 %
2	Однослойная из стали С 345	17+2*14+12+11+7*10	202,33	84,664 %
3	Однослойная комбинированная (С 255/С 345)	17+2*14+12+11+7*10	202,33	84,644 %
4	Двухслойная стенка (С 255)	12/6+11/6+3*10/6+7*10	224,32	93,8656 %
5	Преднапряженная стенка	16+2*14+3*12+11+5*10	206,73	86,5051 %

Как видно из таблицы, наиболее выгодными являются 2 и 3 варианты, но 2 вариант дороже из-за того, что стенка изготовлена полностью из стали С 345, поэтому принимаем 3 вариант – однослойную комбинированную стенку из сталей С 345 и С 255.

Крыша.

Сравним массы ребер купола:

Расчетная схема	Сечение ребра	Масса ребер, т	Относительная масса , %
3-хшарнирная арка.	Двутавр № 20а.	38,04	66,96 %
2-хшарнирная арка .	Двутавр № 27а.	56,81	100 %

Принимаем сечение ребра - двутавр № 20а.

Определение максимальной нагрузки «р=g Н», при которой будет достигнуто предельное состояние в зоне «нижнего узла».

В зоне «нижнего узла» напряженное состояние определяется изгибающим моментом «М1» (вдоль образующей), N2 - кольцевое растягивающее усилие, N1 – меридиональное сжимающее усилие.

Момент «М1» определяется методом сил по общеизвестной методике, соответственно следующей расчетной схеме:

N2 =g*y*r

N1=p*r/2

Для резервуара V=20000 м3 (при Н=1788 см, tc=1,6 см,r=1995 см,р=1,54 кг/см2)

M1=459 кгсм; Q1=0,45 кн.

Если предположить, что стенка жестко защемлена (нет ни угла поворота, нисмещения вдоль днища), то

 М1=(1-by)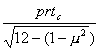 =1555 кгсм;

b=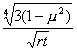=0,02275;

m=0,3; r=1995; tc=1,6; p=1,54.

Q=(2b - 1/H) = 69,8 кг/см;

Напряжение в нижней части стенки

s1= - -=2067<3780;

sт=3300 ст.09Г2С-12

Чтобы s1=sт (на краю) надо приложить нагрузку

Рпр=р*к=1,61*3300/s1=2,81 кн/см.

Однако, теоретически, несущая способность стенки не исчерпаема.Она будет исчерпана, когда s=sт по всему сечению,т.е. будет иметь место пластический шарнир:

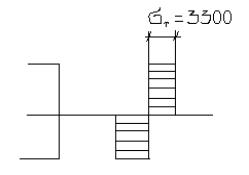Причем этому предельному состоянию будет соответствовать предельный момент:

Мт=3300*1,6^2/4=2112 кгсм.

На расстоянии «S» от края будет иметь место максимальное усилие:

N2=3300*1.6=5280кн/см;

qпр=5280/1995=2,628 кг/см2.

Рассмотрим несколько предельных состояний :

В реальном резервуаре «предельное состояние» находится между 1 и 2. Если бы были известны S, P, и Q, то мы знали бы «точно» 1 и 2 предельнные состояния.

При расчете использована методика, изложенная в книге « Листовые конструкции». Приняты следующие допущения:

N2т и М1т – не зависят друг от друга;

Вместо реальной диаграммы принята диаграмма Прандля.

N2т=sт*t; M1т=sт*t2/4; qпр= N2т/r.

Для каждой из схем 1 и 2 рассмотрим условие:

Первая схема.

1. åМа=0; М1т -  +  = 0;

2. åх =0; +Q – pS = 0;

3. åD=0; dQ*Q - dp*P - dм*М1т=0.

Вторая схема.

1. 2*М1т -  +  = 0;

2. +Q – pS = 0;

3. dQ*Q - dp*P - dм*М1т=0.

Эти системы позволяют найти «р», «S» и «Q».

1 схема: р=4,17 кг/см2; Q=125кг; S=44 см.

2 схема: р=16,7 кг/см2; Q=355,8 кг; S=23,1 см.

В обеих схемах М1т 2112 кгсм.

Тогда в реальном резервуаре:

S=39,5 см; р=10,5 кг/см2; Q=240 кг; М1т=2112 кгсм.

Таким образом, если не учитывать опасность хрупкого разрушения, опасность малоцикловой усталости, то можно считать, что теоретический коэффициент запаса равен:

Кз= ;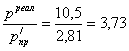

Какой коэффициент запаса на самом деле с учетом вышеуказанных факторов пока сказать нельзя.

[В.В.1]