Навигация
Мария Корнева
Введение
В физике часто используются очевидные положения, которые представляются достаточно ясными и не требуют последующего обоснования. Это не всегда оправдано, поскольку есть случаи, приводящие к парадоксальным следствиям. Тогда приходится возвращаться к анализу «очевидных положений» и допущений. Одним из таких очевидных положений является вывод преобразования Лоренца.
Эйнштейн в начале своего вывода преобразования Лоренца повторяет допущение: «пусть x'=x–vt» [1]. Мы не будем останавливаться на логике доказательства, а сразу приведем конечный результат:
x' = (x – vt)/(1 – v2/c2)1/2.
Сравнивая эти два выражения, легко установить их несоответствие.
В математике есть метод доказательства от противного. Если мы в начале доказательства полагаем, что a=b, а приходим к выводу, что a=k∙b≠b, то:
либо исходная посылка не верна;
либо имеет место ошибка в доказательстве.
Именно эта ошибка Лоренца имеет место при выводе преобразования Лоренца. Она повторяется у Пуанкаре, у Эйнштейна и других. Но почему никто не обратил внимания на это несоответствие?
Рассмотрим другой подход.
1. Класс преобразований
Решение любой математической задачи опирается на теорему о существовании и единственности решения. Решение может не существовать, может существовать множество решений или же существует одно единственное. Мы поставим следующую задачу. Будем искать класс преобразований 4-координат, при которых уравнения Максвелла сохраняют свою форму в соответствии с принципом Галилея-Пуанкаре [2]. Задача существования преобразования уже решена, т.к. существует преобразование Лоренца.
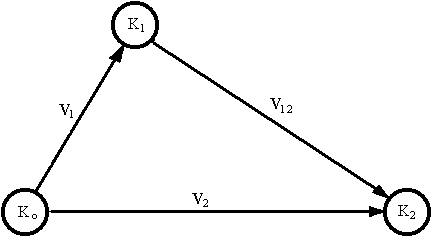
Рассмотрим две инерциальные системы отсчета K и K', которые движутся друг относительно друга со скоростью V. Пространственно-временные координаты системы K(x; y; z; ct) должны быть связаны с соответствующими координатами K'(x'; y'; z'; ct') с помощью матрицы преобразования [T(V/c)].
| [X'] = [T(V/c)][X], | (1.1) |
где: [X] и [X'] – вектор столбцы 4-координат K и K'; [Т(V/c)] – матрица преобразования, зависящая только от скорости относительного движения сравниваемых инерциальных систем.
К матрице [Т] предъявляются следующие требования:
определитель матрицы должен быть равным единице; det[T]=1;
должна существовать матрица обратного преобразования из K' в K, т.е. матрица [Т(V/c)]–1;
матрица обратного преобразования должна получаться заменой V на –V в матрице [T(V/c)]. Это следует из равноправия инерциальных систем отсчета [T(V/c)]–1=[T(–V/c)].
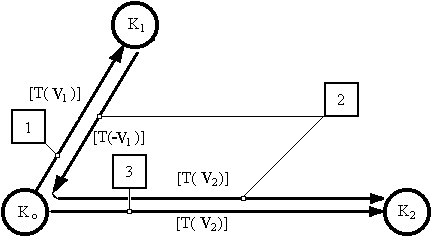
Из этих условий можно определить общий вид матрицы преобразований координат и времени, сохраняющей инвариантную форму уравнений Максвелла. Уравнения, соответствующие (1.1), можно записать в следующей форме:
| x' = x(1 + f2(V/c))1/2 – f(V/c)ct; y' = y; z' = z; ct' = ct(1 + f2(V/c))1/2 – f(V/c)x, | (1.2) |
где f(V/c) есть нечетная функция относительно V/c. При малых скоростях V/c эта функция равна f≈V/c.
Перечисленных выше условий не достаточно, к сожалению, чтобы определить явный вид функции f(V/c). Она может быть V/c, или sin(V/c), или sh(V/c) и т.д. В частном случае, когда f=V/(c2–V2)1/2, мы получаем преобразование Лоренца*.
* В действительности имеет место более широкий класс преобразований: x'=x(1+f1∙f2)1/2–f1ct; y'=y; z'=z; ct'=ct(1+f1f2)1/2–f2∙x где f1 и f2 – некоторые нечетные функции относительно V/c. При малых скоростях эти функции равны V/c. Однако если положить, что пространственная координата x и временная ct имеют одинаковые математические свойства, тогда f1=f2=f. В дальнейшем мы будем придерживаться этой гипотезы.
2. Физическая интерпретация преобразования
В наших предшествующих исследованиях (например, [2], [3] и других) мы выяснили физический смысл преобразований Лоренца. Его можно распространить на любое преобразование найденного выше класса. Напомним:
Системы отсчета K и K', связываемые преобразованием (1.2) этого класса, равноправны для электромагнитных волн, описываемых уравнениями Максвелла.
Время во всех инерциальных системах едино.
Пространство является общим и евклидовым для всех инерциальных систем отсчета.
Никаких изменений пространства и времени при переходе из одной инерциальной системы отсчета в другую не происходит.
Скорость света во всех инерциальных системах отсчета одинакова (принцип Галилея-Пуанкаре [2]).
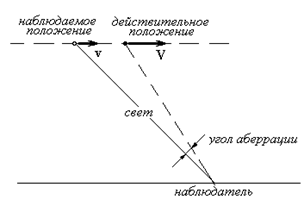
Преобразование (1.2) описывает наблюдаемые в неподвижной системе отсчета процессы и явления, которые протекают в движущейся системе отсчета. Информация, доставляемая нам световыми лучами, может иметь искажения из-за эффекта Доплера и искажения фронта светового потока.
Рассмотрим некоторые явления, связанные с переходом из одной инерциальной системы отсчета в другую.
Изменение длины движущейся линейки
Пусть в K' имеется линейка длиной Δx', ориентированная вдоль вектора скорости относительного движения систем отсчета K и K'. Величина Δx' есть истинная (действительная) длина линейки. В системе K мы будем видеть (измерять) другую «длину» движущейся линейки. Новая длина будет зависеть от следующих величин: f(V/c) и θ. Угол θ образован вектором скорости относительного движения V и вектором скорости света, идущего от движущейся линейки к неподвижному наблюдателю в системе отсчета наблюдателя.
| Δx = Δx' / [(1 + f 2)1/2 – f∙cos θ]. | (2.1) |
Отсюда следует, что существует угол наблюдения θ0 (критический угол), при котором мы измерим истинную длину движущейся линейки.
Δx = Δx' при θ0 = arccos [(1 + f 2)1/2 – 1) / f].
При θ<θ0 линейка будет «казаться» длиннее, а при θ>θ0 – короче. Это обусловлено величиной искажения фронта волны. Интересно отметить, что этот критический угол θ0 получается при условии, что θ0=π–θ'.
Эффект Доплера
Пусть в системе K' имеется генератор, излучающий монохроматический свет с частотой ω0. В системе K мы будем измерять другую частоту (интервалы времени):
| ω = ω0 / [(1 + f 2) – f∙cos θ]. | (2.2) |
Как и в предыдущем случае эффект Доплера отсутствует (ω=ω0) при угле наблюдения θ=θ0.
Похожие работы
... позитивистских, а позже – прагматических настроений [14], [15], связанных с отходом от материалистического миропонимания. Поэтому не удивительно, что идея Эйнштейна о необходимости распространения преобразования Лоренца на все без исключения явления материального мира (требование от уравнений физики обязательной лоренц-ковариантной формы) было принято некритически большинством ученых. А было ли ...
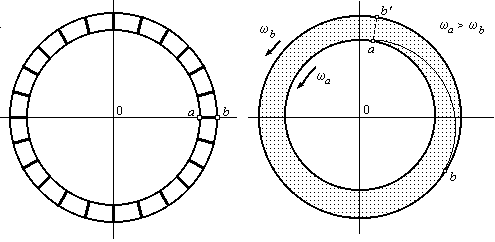
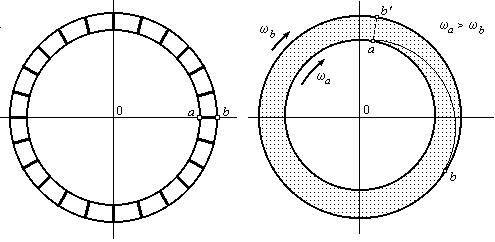
... . Что касается «сжатия» окружности диска и нарастающего во времени «смещения» друг относительно друга смежных кольцевых слоев диска, то их принципиально не может существовать. У интерпретаторов парадокса Эренфеста не все в порядке со «здравым смыслом». Преобразование Лоренца нельзя применять формально (догматически), не сообразуясь с физикой анализируемых процессов (со здравым смыслом). 6. ...
... дать логически последовательное объяснение парадоксам и прикрывают его фиговыми листочками математических формул, мы вскрываем застарелые «язвы», разъедающие СТО и физику. Наш научный задел размещен на сайте [14]. Новый подход к объяснению релятивистских явлений возвращает нас к классической механике Ньютона. Новый подход к релятивистским явлениям затронет и классическую электродинамику. Причина ...
... наблюдателю будет казаться, что часы движущегося наблюдателя отстают от его часов. Это объективное явление. Зависимость замедления наблюдаемого хода часов движущегося наблюдателя от относительной скорости инерциальных систем отсчета есть физическая закономерность. Вербально эту закономерность можно описать следующим образом: «Наблюдаемое изменение темпа времени в движущейся системе отсчета есть ...

0 комментариев