Навигация
Кажущаяся и истинная скорость света
3. Кажущаяся и истинная скорость света
Относительную скорость движения инерциальных систем можно измерить разными способами.
Первый способ
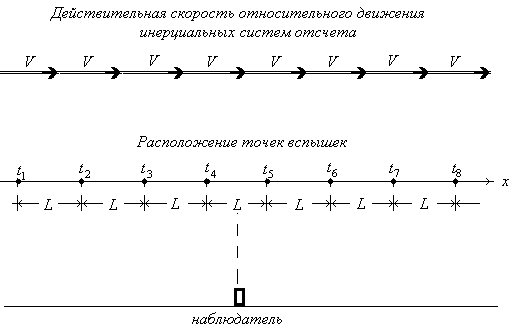
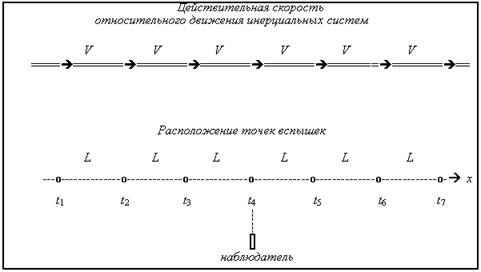
Он рассмотрен в [2]. В системе K' имеется неподвижный источник, который излучает короткие световые импульсы через равные интервалы времени ΔT'. В системе K мы будем видеть траекторию, «разделенную» этими вспышками на равные интервалы времени Δx, которые покоятся в системе K. Измеряя интервал времени между вспышками ΔT, в системе K можно определить наблюдаемую (или кажущуюся) скорость движения инерциальных систем. «Кажущейся» мы называем эту скорость потому, что мы наблюдаем в системе K «искаженный» движением интервал времени ΔT. Эта скорость будет зависеть от угла наблюдения θ.
Второй способ
Мы можем разместить линейку длиной Δx' в системе K', ориентированную вдоль скорости относительного движения инерциальных систем. В системе K траекторией движения будет прямая линия, на которой мы зафиксируем неподвижную точку. Измеряя время ΔT, за которое линейка проходит эту точку, можно вычислить кажущуюся скорость движения. «Кажущейся» мы называем эту скорость потому, что мы наблюдаем в системе K «искаженную» движением длину отрезка Δx. Эта скорость будет также зависеть от угла наблюдения θ.
Независимо от способа измерения имеют место следующие выражения для этой скорости:
| vкаж = Δx / ΔT [(1 + f 2) – f∙cos θ]. | (3.1) |
Как и ранее, при критическом угле наблюдения θ = θ0 мы будем измерять истинную (или действительную) скорость относительного движения V инерциальных систем отсчета. Скорость V есть галилеевая скорость относительного движения инерциальных систем отсчета.
| vкаж (θ0) = Δx / ΔT' = V; (1-й способ) | (3.2) |
| vкаж (θ0) = Δx' / ΔT = V. (2-й способ) | (3.3) |
Это не удивительно, поскольку интервалы времени и длины при критическом угле наблюдения θ=θ0 отображаются безо всяких искажений. Здесь как бы реализуется преобразование Галилея.
Итак:
vкаж = V / [(1 + f 2) – f∙cos θ].
Рассмотрим те же два случая с точки зрения формального подхода. Рассмотрим уравнение (1.2) в приращениях.
Δx' = Δx(1 + f 2(V/c))1/2 – f (V/c) cΔt; cΔt' = cΔt(1 + f 2(V/c))1/2 – f (V/c)Δx.
1-й случай. Мы рассматриваем в K' неподвижную точку. Следовательно, Δx'=0. После простых выкладок получим выражения для кажущейся и действительной скоростей:
| vкаж = Δx / ΔT(90о) = cf / (1 + f 2)1/2 = cV / (1 + V 2)1/2; θ = 90о; | (3.4) |
| vдейств = Δx / ΔT' = cf = V. | (3.5) |
Такие же выражения мы получим и для второго случая.
Итак, выражение (3.4) есть кажущаяся скорость при θ = 90о. Выражение (3.5) есть действительная (галилеева) скорость. Отсюда нетрудно найти функцию f. Она равна
| f = V/c. | (3.6) |
Заметим, что действительная скорость вычисляется через величины, измеренные в собственной системе отсчета.
1-й способ: ΔT' – время, измеренное в K' для неподвижного источника; Δx – неподвижное расстояние, измеренное в системе K. Мы хотим обратить внимание на следующий факт. Интервал времени измерен в одной и той же неподвижной точке пространства, а длина отрезка в системе отсчета, где отрезок неподвижен.
2-й способ: Δx' – длина неподвижного отрезка в системе K'; ΔT – интервал времени, измеренный в неподвижной точке системы K. Здесь, как и в предыдущем случае, интервал времени измерен в одной и той же неподвижной точке пространства, а длина отрезка в системе отсчета, где отрезок неподвижен.
Величины, измеренные при этих условиях, являются характеристиками сущности. В то же время, интервалы времени и длины отрезков, измеренные при других условиях, являются характеристиками явлений [4]. Они зависят от условий наблюдения (от угла наблюдения и от скорости относительного движения). По этой причине мы имеем дело с двумя видами скорости: истинной (галилеевой) скоростью относительного движения V инерциальных систем отсчета и наблюдаемой (кажущейся) скоростью vкаж, которая «искажена» из-за изменений параметров светового луча при переходе наблюдателя из одной системы отсчета в другую.
Таким образом, нам удалось записать явное выражение для f через истинную (галилеевую) скорость относительного движения инерциальных систем отсчета (3.6) и найти явный вид преобразования (1.2). Это преобразование называется модифицированным [2]. Оно существенно отличается от преобразования Лоренца. Именно оно должно использоваться для описания релятивистских явлений.
Похожие работы
... позитивистских, а позже – прагматических настроений [14], [15], связанных с отходом от материалистического миропонимания. Поэтому не удивительно, что идея Эйнштейна о необходимости распространения преобразования Лоренца на все без исключения явления материального мира (требование от уравнений физики обязательной лоренц-ковариантной формы) было принято некритически большинством ученых. А было ли ...
... . Что касается «сжатия» окружности диска и нарастающего во времени «смещения» друг относительно друга смежных кольцевых слоев диска, то их принципиально не может существовать. У интерпретаторов парадокса Эренфеста не все в порядке со «здравым смыслом». Преобразование Лоренца нельзя применять формально (догматически), не сообразуясь с физикой анализируемых процессов (со здравым смыслом). 6. ...
... дать логически последовательное объяснение парадоксам и прикрывают его фиговыми листочками математических формул, мы вскрываем застарелые «язвы», разъедающие СТО и физику. Наш научный задел размещен на сайте [14]. Новый подход к объяснению релятивистских явлений возвращает нас к классической механике Ньютона. Новый подход к релятивистским явлениям затронет и классическую электродинамику. Причина ...
... наблюдателю будет казаться, что часы движущегося наблюдателя отстают от его часов. Это объективное явление. Зависимость замедления наблюдаемого хода часов движущегося наблюдателя от относительной скорости инерциальных систем отсчета есть физическая закономерность. Вербально эту закономерность можно описать следующим образом: «Наблюдаемое изменение темпа времени в движущейся системе отсчета есть ...

0 комментариев