Навигация
Стратифицированный анализ и описание КММ системного элемента
2.5. Стратифицированный анализ и описание КММ системного элемента
Концептуальные метамодели элемента, основанные на записи ( 1 ), могут образовывать некоторые иерархии. Уровни таких иерархий определяются степенью ( этапами ) конкретизации свойств элемента. Ранжирование КММ ( 1 ) по шкале "Абстрактное - Конкретное" на основе метода стратификации, следовательно, приводит к иерархической дедуктивной системе концептуальных метамоделей. Такая система может быть использована для математического моделирования конкретных элементов как некоторый исходный базовый инвариант, интерпретируемый в конкретную математическую модель.
В зависимости от степени конкретизации, сформируем дедуктивную систему, вклю-чающую следующие уровни КММ элемента ![]() :
:
КММ элемента ![]() на теоретико-системном уровне ( ТСУ );
на теоретико-системном уровне ( ТСУ );
КММ элемента ![]() на уровне непараметрической статики ( УНС );
на уровне непараметрической статики ( УНС );
КММ элемента ![]() на уровне параметрической статики ( УПС );
на уровне параметрической статики ( УПС );
КММ элемента ![]() на уровне непараметрической динамики ( УНД );
на уровне непараметрической динамики ( УНД );
КММ элемента ![]() на уровне параметрической динамики ( УПД ).
на уровне параметрической динамики ( УПД ).
Рассмотрим более подробно КММ на каждом из перечисленных уровней.
КММ теоретико-системного уровня
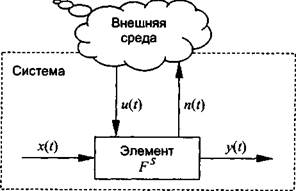
Наиболее общую и абстрактную форму описания функционирования системного
элемента ![]() дает концептуальная метамодель теоретико-системного уровня ( ТСУ ). Это описание включает векторное множество входных воздействий на элемент
дает концептуальная метамодель теоретико-системного уровня ( ТСУ ). Это описание включает векторное множество входных воздействий на элемент ![]()
![]()
и векторное множество выходных реакций ( откликов ) элемента ![]()
![]() .
.
Кроме того, на рассматриваемом уровне абстракции учитывается факт связности векторного множества ![]() с соответствующим векторным множеством
с соответствующим векторным множеством ![]() посредством отображения "". Однако, отображение "" не указывает каким образом рассматриваемые множества связаны.
посредством отображения "". Однако, отображение "" не указывает каким образом рассматриваемые множества связаны.
Таким образом, КММ теоретико-системного уровня задаются тройкой
![]() . ( 2 )
. ( 2 )
КММ уровня непараметрической статики
Второй уровень представления КММ включает в рассмотрение отображение ![]() , определяющее правила преобразования входов
, определяющее правила преобразования входов ![]() в выходы
в выходы ![]() , т.е. что необходимо сделать, чтобы при условии
, т.е. что необходимо сделать, чтобы при условии ![]() получить
получить ![]() , адекватное целевому функционированию элемента
, адекватное целевому функционированию элемента ![]() . В общем случае
. В общем случае ![]() - отображение может быть представлено скалярной или векторной функцией, а также функционалом или оператором. Концептуальная метамодель уровня непараметрической статики, следовательно, представляется кортежем вида
- отображение может быть представлено скалярной или векторной функцией, а также функционалом или оператором. Концептуальная метамодель уровня непараметрической статики, следовательно, представляется кортежем вида
![]() . ( 3 )
. ( 3 )
Раскрытие структуры преобразования вида ![]() является основной задачей КММ уровня
является основной задачей КММ уровня ![]() . Рассмотрим в качестве иллюстрации функциональное описание элемента
. Рассмотрим в качестве иллюстрации функциональное описание элемента ![]() , представленное скалярной функцией
, представленное скалярной функцией ![]() , причем:
, причем: ![]() .
.
Функционирование элемента ![]() (
( ![]() ) на УНС описывается как отображение
) на УНС описывается как отображение ![]() . Это отображение называется функцией, если оно однозначно. Условия однозначности определяются следующим образом. Пусть заданы пары значений
. Это отображение называется функцией, если оно однозначно. Условия однозначности определяются следующим образом. Пусть заданы пары значений
сигналов "вход - выход":
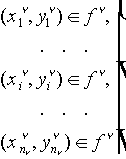 ( 4 )
( 4 )
Если из условия ( ![]() ), следует, что (
), следует, что ( ![]() ), то отображение
), то отображение ![]() однозначно. Значение величины
однозначно. Значение величины ![]() в любой из пар
в любой из пар ![]() называется функцией от данного
называется функцией от данного ![]() . Общий вид записи функции
. Общий вид записи функции ![]() позволяет дать формальное
позволяет дать формальное
определение функции элемента ![]() в скалярной форме представления
в скалярной форме представления
![]() ( 5 )
( 5 )
Таким образом, КММ ( 3 ) проинтерпретирована в КММ того же уровня, но в скалярной форме функционального представления. Отметим, что богатство концептуальных метамоделей ![]() функционирования системного элемента
функционирования системного элемента ![]() (
( ![]() ) на уровне непараметрической статики определяется многообразием ее интерпретаций на математическом, логическом или логико-математическом языках описания ( представления )
) на уровне непараметрической статики определяется многообразием ее интерпретаций на математическом, логическом или логико-математическом языках описания ( представления )
![]() - отображения.
- отображения.
КММ уровни параметрической статики
Дальнейшая конкретизация КММ функционирования системного элемента ![]()
осуществляется за счет включения в рассмотрение функциональных параметров ![]() , определяющих статические режимы. Для элемента
, определяющих статические режимы. Для элемента ![]() рассматриваются три группы параметров
рассматриваются три группы параметров
![]() ( 6 )
( 6 )
где ![]() - совокупность параметров {
- совокупность параметров { ![]() } входных воздействий
} входных воздействий ![]()
![]() - совокупность параметров {
- совокупность параметров { ![]() } выходных реакций ( откликов )
} выходных реакций ( откликов ) ![]()
![]() - совокупность параметров {
- совокупность параметров { ![]() } отображения
} отображения ![]() .
.
Перечни ( номенклатура ) параметров ![]() и их значений определяются для каждого типа конкретной модели
и их значений определяются для каждого типа конкретной модели ![]() . Для
. Для ![]() - отображения, по аналогии со структурными моде- лями, вводится понятие конфигурации. С учетом параметрического описания и интерпретаций КММ задается четверкой
- отображения, по аналогии со структурными моде- лями, вводится понятие конфигурации. С учетом параметрического описания и интерпретаций КММ задается четверкой
![]() ( 7 )
( 7 )
КММ уровня непараметрической динамики
Следующий, четвертый уровень конкретизации КММ функционирования системного элемента ![]() определяется учетом в модели его динамических свойств. Динамика элемента
определяется учетом в модели его динамических свойств. Динамика элемента ![]() рассматривается в нескольких аспектах. Первый аспект характеризуется реакцией элемента
рассматривается в нескольких аспектах. Первый аспект характеризуется реакцией элемента ![]() на динамику изменения входных воздействий
на динамику изменения входных воздействий ![]()
при неизменном отображении ![]() , т.е. когда
, т.е. когда ![]() - скалярная или векторная функция. Второй аспект определяется реакцией элемента
- скалярная или векторная функция. Второй аспект определяется реакцией элемента ![]() на входные ( статические
на входные ( статические ![]() или динамические
или динамические ![]() ) воздействия при времязависимом отображении
) воздействия при времязависимом отображении ![]() , т.е. когда
, т.е. когда ![]() -
-
функционал или оператор, зависящий от времени ![]() .
.
При изложенных условиях КММ рассматриваемого уровня абстракции представляется кортежем, включающем следующие четыре компоненты
![]() ( 8 )
( 8 )
Отметим, что на данном уровне представления КММ время ![]() указывает на факт
указывает на факт
наличия динамических свойств, но не характеризует их конкретно.
КММ уровня параметрической динамики
Последний - пятый уровень дедуктивного представления КММ функционирования системного элемента ![]() , определяемый как уровень параметрической динамики, включает все рассмотренные ранее аспекты модели, представляемые кортежем ( 1 )
, определяемый как уровень параметрической динамики, включает все рассмотренные ранее аспекты модели, представляемые кортежем ( 1 )
![]() .
.
В КММ рассматриваемого уровня выполняются условия концептуальной полноты представления функциональных свойств элемента ![]() . Интерпретация та- кой модели на семантическом, синтаксическом, качественном и количественном уровнях дает возможность порождать ( генерировать ) любые конкретные математические модели функционирования системного элемента.
. Интерпретация та- кой модели на семантическом, синтаксическом, качественном и количественном уровнях дает возможность порождать ( генерировать ) любые конкретные математические модели функционирования системного элемента.
Отметим, что выражения ( 1 ), ( 2 ), ( 3 ), ( 7 ) и ( 8 ) могут быть представлены в форме традиционных аналитических зависимостей вида
![]() ( 9 )
( 9 )
Выводы
Таким образом, концептуальное метамоделирование функционирования системного элемента ![]() на основе дедуктивного подхода приводит к пятиуровневой иерархии моделей, представленной на рис. .
на основе дедуктивного подхода приводит к пятиуровневой иерархии моделей, представленной на рис. .
Практическое использование представленных выше КММ для моделирования функций системных элементов ![]() осуществляется посредством их ретрансляции в тер-минах выбранного математического языка и последующей интерпретации на четырех перечисленных выше уровнях конкретизации.
осуществляется посредством их ретрансляции в тер-минах выбранного математического языка и последующей интерпретации на четырех перечисленных выше уровнях конкретизации.
Похожие работы
... и количественной происходит поэтапная трансформация АМО, например, концептуальной метамодели (КММ) функциональной системы , в конкретную математическую модель (ММ) конкретного объекта моделирования. Глава II Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является ...
... модель (ММ) конкретного объекта моделирования.Глава II Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, простой, простейший, ...
... , динамические и статические, простые и сложные, естественные и искусственные, с управлением и без управления, непрерывные и дискретные, детерминированные и стохастические, открытые и замкнутые. Основы системного анализа Деление систем на физические и абстрактные позволяет различать реальные системы (объекты, явления, процессы) и системы, являющиеся определенными отображениями (моделями) ре ...
... того, имеется ряд так называемых системных атрибутов, относящихся не к отдельным объектам, а к модели в целом. Значения атрибутов всех объектов модели по окончании моделирования Выводятся в стандартный отчет GPSS/PC. Большая часть атрибутов дос- тупна программисту и составляет так называемые стандартные число- вые атрибуты (СЧА), 0которые могут использоваться в ...
0 комментариев